Module 2
Differential Calculus- I
Limits
1). Compute limx→−2(3x2+5x−9)
Solution:
First, use property 2 to divide the limit into three separate limits. Then use property 1 to bring the constants out of the first two. This gives,
Lim x→−2(3x2+5x−9)=lim x→−2(3x2)+lim x→−2(5x)−lim x→−2(9)
=3(−2)2+5(−2)−(9)
= -7
2). Find the limits of limx→3 [x(x+2)].
Solution: limx→3 [x(x+2)] = 3(3+2) = 3 x 5 = 15
Continuous Function
A function f(x) is said to be continuous at x = a if
i) f(a) exist is function must exist at x = a
Differentiation
Let y = f(x) be any function A function f(x) is said to be differentiable at x = a if
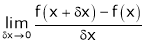 is exist and it is denoted by
is exist and it is denoted by 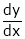
Note:-
A differentiable function is always continuous but the converse need not be true.
If
i) f(x) is continuous in the closed [a, b]
ii) f(x) is differentiable in (a, b) &
iii) f(a) = f(b)
Then there exist at least one value ‘c’ in (a, b) such that f’(c) = 0.
Exercise 1
Verify Rolle’s theorem for the function f(x) = x2 for 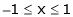
Solution:
Here f(x) = x2; 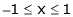
i) Since f(x) is algebraic polynomial which is continuous in [-1, 1]
ii) Consider f(x) = x2
Diff. w.r.t. x we get
f'(x) = 2x
Clearly f’(x) exists in (-1, 1) and does not becomes infinite.
iii) Clearly
f(-1) = (-1)2 = 1
f(1) = (1)2 = 1
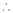 f(-1) = f(1).
f(-1) = f(1).
Hence by Rolle’s theorem, there exist 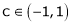 such that
such that
f’(c) = 0
i.e. 2c = 0
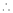 c = 0
c = 0
Thus 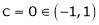 such that
such that
f'(c) = 0
Hence Rolle’s Theorem is verified.
Exercise 2
Verify Rolle’s Theorem for the function f(x) = ex(sin x – cos x) in 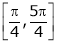
Solution:
Here f(x) = ex(sin x – cos x); 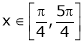
i) Ex is an exponential function continuous for every 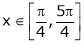 also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in
also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in 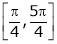 and Hence ex(sin x – cos x) is continuous in
and Hence ex(sin x – cos x) is continuous in 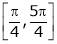 .
.
ii) Consider
f(x) = ex(sin x – cos x)
diff. w.r.t. x we get
f’(x) = ex(cos x + sin x) + ex(sin x + cos x)
= ex[2sin x]
Clearly f’(x) is exist for each 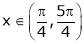 & f’(x) is not infinite.
& f’(x) is not infinite.
Hence f(x) is differentiable in  .
.
iii) Consider
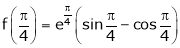
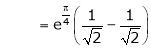
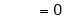
Also,

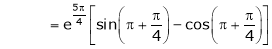


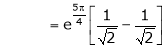

Thus 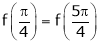
Hence all the conditions of Rolle’s theorem are satisfied, so there exist 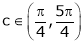 such, that
such, that
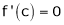
i.e. 
i.e. sin c = 0


But
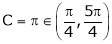
Hence Rolle’s theorem is verified.
Exercise 3
Verify whether Rolle’s theorem is applicable or not for

Solution:
Here f(x) = x2; 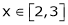
i) X2 is an algebraic polynomial hence it is continuous in [2, 3]
ii) Consider
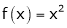
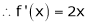
F’(x) exists for each 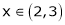
iii) Consider
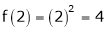
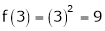
Thus  .
.
Thus all conditions of Rolle’s theorem are not satisfied Hence Rolle’s theorem is not applicable for f(x) = x2 in [2, 3]
Exercise 4
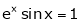
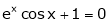
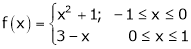
Lagrange’s Mean value Theorem:-
Statement:- If
i) f(x) is continuous in [a, b]
ii) f(x) is differentiable in (a, b) then there exist at least one value 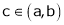 such that
such that
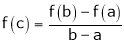
Exercise 5
Verify the Lagrange’s mean value theorem for
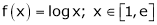
Solution:
Here 
i) Clearly f(x) = log x is logarithmic function. Hence it is continuous in [1, e]
ii) Consider f(x) = log x.
Diff. w.r.t. x we get,
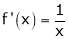
Clearly f’(x) exists for each value of  & is finite.
& is finite.
Hence all conditions of LMVT are satisfied Hence at least 
Such that
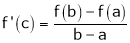
i.e. 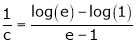
i.e. 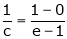
i.e. 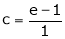
i.e. 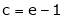
since e = 2.7183
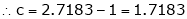
Clearly c = 1.7183 
Hence LMVT is verified.
Exercise 6
Verify mean value theorem for f(x) = tan-1x in [0, 1]
Solution:
Here 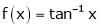 ;
; 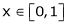
i) Clearly 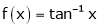 is an inverse trigonometric function and hence it is continuous in [0, 1]
is an inverse trigonometric function and hence it is continuous in [0, 1]
ii) Consider 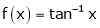
diff. w.r.t. x we get,

Clearly f’(x) is continuous and differentiable in (0, 1) & is finite
Hence all conditions of LMVT are satisfied, Thus there exist 
Such that
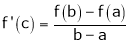
i.e. 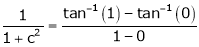
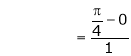
i.e. 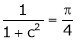
i.e. 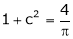
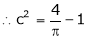
i.e. 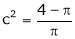
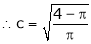
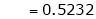
Clearly 
Hence LMVT is verified.
Meaning of sign of Derivative:
Let f(x) satisfied LMVT in [a, b]
Let x1 and x2 be any two points laying (a, b) such that x1< x2
Hence by LMVT, 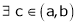 such that
such that 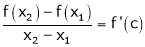
i.e. 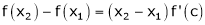 … (1)
… (1)
Cast I:
If 
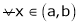 then
then 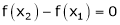
i.e. 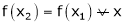
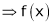 is constant function
is constant function
Case II:
If 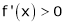
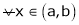 then from equation (1)
then from equation (1)
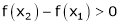
i.e. 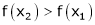
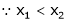 means x2 - x1> 0 and
means x2 - x1> 0 and 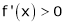
Thus for x2> x1

Thus f(x) is increasing function is (a, b)
Case III:
If 

Then from equation (1)
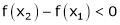
i.e. 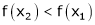
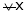
since 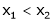 and
and 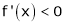 then
then 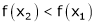
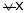 hence f(x) is strictly decreasingfunction.
hence f(x) is strictly decreasingfunction.
Exercise 7
Prove that
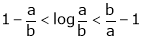
And hence show that
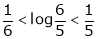
Solution:
Let 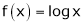 ;
; 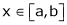
i) Clearly 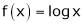 is a logarithmic function and hence it is continuous also
is a logarithmic function and hence it is continuous also
ii) Consider 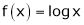
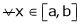
diff. w.r.t. x we get,
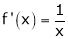
Clearly f’(x) exist and finite in (a, b) Hence f(x) is continuous and differentiable in (a, b). Hence by LMVT 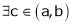
Such that

i.e. 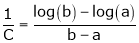
i.e. 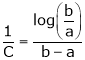
since
a < c < b
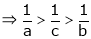
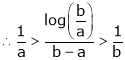
i.e. 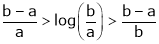
i.e. 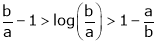
i.e. 
i.e. 
Hence the result
Now put a = 5, b = 6 we get

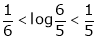
Hence the result
Exercise 8
Prove that 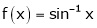 ,
, 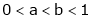 use mean value theorem to prove that,
use mean value theorem to prove that,
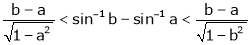
Hence show that
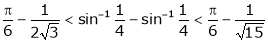
Solution:
i) Let f(x) = sin-1x; 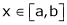
ii) Clearly f(x) is inverse trigonometric function and hence it is continuous in [a, b]
iii) Consider f(x) = sin-1x
diff. w.r.t. x we get,
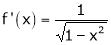
Clearly f’(x) is finite and exists for 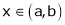 . Hence by LMVT,
. Hence by LMVT, 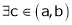 such that
such that
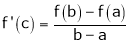
i.e. 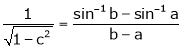
since a < c < b
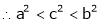

i.e. 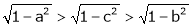
i.e. 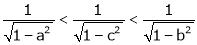
i.e. 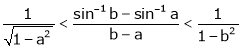
i.e. 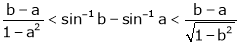
Hence the result
Put 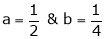 we get
we get
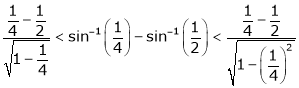
i.e. 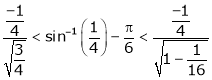
i.e. 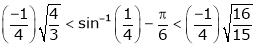
i.e. 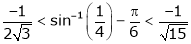
i.e. 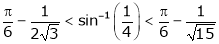
Hence the result
Lagrange’s Mean Value Theorem:
Statement:
Let f: [a,b]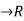 be a continuous function ,differentiable on the open interval (a,b).Thenthere exista some c
be a continuous function ,differentiable on the open interval (a,b).Thenthere exista some c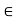 (a,b) such that
(a,b) such that
f’(c) =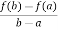
proof:
we reduce the problem to Rolle’s theorem by using auxillary functions.
Consider,
g(x) = f(x)- 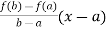
note: g(a)=g(b)=f(b)
by rolle’s theorem therexists, c in (a,b) such that g’(c) =0 or s
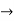 f’(c) -
f’(c) -  = 0
= 0
Which simplifies to,
f’(c) = 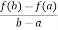
exercise 9:
use lagranges mean value theorem to determine a point P on the curve y=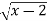
where the tangent is parallel to the chord joining (2,0) and (3,1)
solution:
consider y= 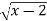 in [2,3]
in [2,3]
(i) Function is continuos in[2,3] as algebraic expression with positive exponent is continuous.
(ii) y’=  , y’ exists in (2,3) hence the function is derivable in (2,3)
, y’ exists in (2,3) hence the function is derivable in (2,3)
hence the condition of LMV theorem is satisfied.
Hence, there exists one c in (2,3) such that 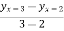 =
= 
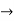
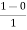 =
= 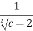
 4(c-2) = 1
4(c-2) = 1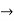 4c=9
4c=9  c= 4/9
c= 4/9
 for x = 9/4, tangent is parallel to the chord joining (2,0) and (3,1)
for x = 9/4, tangent is parallel to the chord joining (2,0) and (3,1)
Substituting in (i) we get,
Y= 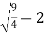 =
= 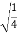 = ½
= ½
Exercise 10:
Verify lagrange’s mean value theorem for the following function
f(x) = 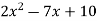
putting x=a=2 and x=b=5 ,we get
f(2) = 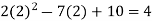
f(5) = 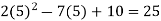
clearly,
f(2) 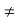 f(5)
f(5)
since f(x) is a polynomial function in x, then f(x) is continuous in [2,5].
And f(x) is polynomial in x,then it can be differentiatie such that f’(x) = 4x-7
Then by LMV theorem there exists c 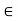 (2,5) such that’
(2,5) such that’
f’ (c) = 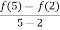
4c-7 = 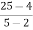
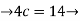 c=3.75
c=3.75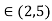
Hence lagrange’s mean value theorem is verified for f(x) in [2,5].
Cauchy’s Mean Value Theorem:
Statement:-
If f(x) and g(x) are any two functions such that
a) f(x) and g(x) are continuous in (a, b)
b) both f(x) and g(x) are derivable in (a, b)
c) 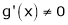
Then for any value of 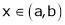 ,
, 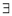 at least
at least 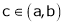 such that
such that

Exercise 11
Verify Cauchy mean value theorems for 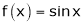 &
&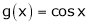 in
in 
Solution:
Let 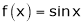 &
&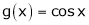 ;
; 
i) Clearly f(x) and g(x) both are trigonometric functions. Hence continuous in 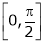
ii) Since 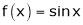 &
&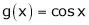
diff. w.r.t. x we get,
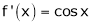 &
&
Clearly both f’(x) and g’(x) exist & finite in 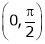 . Hence f(x) and g(x) is derivable in
. Hence f(x) and g(x) is derivable in  and
and
iii) 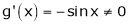
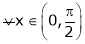
Hence by Cauchy mean value theorem, there exist at least 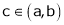 such that
such that
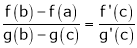
i.e. 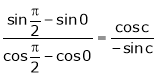
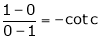
i.e. 1 = cot c

i.e. 
clearly 
Hence Cauchy mean value theorem is verified.
Exercise 12
Considering the functions ex and e-x, show that c is arithmetic mean of a & b.
Solution:
i) Clearly f(x) and g(x) are exponential functions Hence they are continuous in [a, b].
ii) Consider 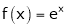 &
&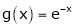
diff. w.r.t. x we get
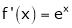 and
and 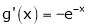
Clearly f(x) and g(x) are derivable in (a, b)
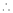 By Cauchy’s mean value theorem
By Cauchy’s mean value theorem 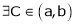 such that
such that
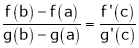
i.e. 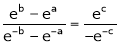
i.e. 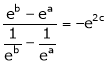
i.e. 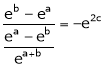
i.e. 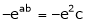
i.e. 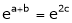
i.e. 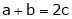
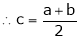
Thus 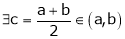
i.e. c is arithmetic mean of a & b.
Hence the result
Exercise 13
Show that 
Prove that if 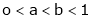
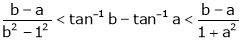 and Hence show that
and Hence show that
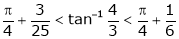
Verify Cauchy’s mean value theorem for the function x2 and x4 in [a, b] where a, b > 0
If for 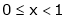 then prove that,
then prove that,
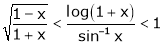
[Hint: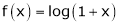 ,
, 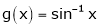 ]
]
Exercise 14:
Find the nth derivative of sin3 x
Sol: we know that sin 3x= 3sin x 4sin3 x = sin3x = 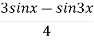
Differentiate n times w.r.t x,
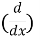 ( sin3 x) =
( sin3 x) = 
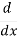 (3 sinx- sin3x)
(3 sinx- sin3x)
= ( -3n. Sin( 3x+ nπ/2) + 3 sin (x+ nπ/2)) nϵz
( -3n. Sin( 3x+ nπ/2) + 3 sin (x+ nπ/2)) nϵz
Exercise 15:
Find the nth derivative of sin 5x. sin 3x.?
Sol: let y = sin 5x.sin 3x=  ( sin 5x.sin 3x)
( sin 5x.sin 3x)
⇒y=  ( cos 2x - cos8x)
( cos 2x - cos8x)
⇒ y= ( cos 2x- cos8x )
( cos 2x- cos8x )
Differentiate n times w.r.t x,
Yn = 
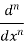 ( cos 2x - cos8x )
( cos 2x - cos8x )
⇒ yn =  ( 2 n (cos( 2x+ nπ/2)- 8n .cos (8x + nπ/2)) nϵz.
( 2 n (cos( 2x+ nπ/2)- 8n .cos (8x + nπ/2)) nϵz.
Successive n th derivative of nth elementary function ie., exponential
Exercise 16:
If y = ae n x + be –nx , then show that y2= n2y
Sol: Y= aenx + be-nx
y 1 = a.n.enx - b.n.e-nx
y2 = an2 enx – bn2 e-nx = n2 (ae nx+ be –nx)
y2= n2y.
Exercise 17:
If y= e-kx/2(a cosnx+ b sinnx) then show that.,y2+ ky1+(n2+ k2/4)y =0
Sol : y= e-kx/2(a cosnx+ b sinnx)
Differentiating w.r.to. x.,
 Y1 = e-kx/2( -an sin nx + bn cos nx) - k/2.y
Y1 = e-kx/2( -an sin nx + bn cos nx) - k/2.y
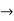 Y1+ k/2.y = ne-kx/2 ( -an sin nx + bn cos nx)
Y1+ k/2.y = ne-kx/2 ( -an sin nx + bn cos nx)  (1)
(1)
Differentiating w.r.to x.,
Y2+ k/2.y1 = ne-kx/2 (-k/2) ( -an sin nx + bn cos nx) + n e-kx/2(-an cosnx- bn sinnx).
= -(k/2) (y1+ k/2 y)- n2 y = - (k/2 y1)- ( k2/4)y- n2y.
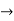 y2 + ky1 +(n2+ k2/4)y = 0.
y2 + ky1 +(n2+ k2/4)y = 0.
Successive differentiation of nth derivative of elementary functions ie., logarithmic
Example 18:
If Y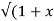 2) = log( x +
2) = log( x + 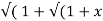 2) ) then show that (1 + x 2) y1 +xy =1
2) ) then show that (1 + x 2) y1 +xy =1
Sol: Y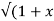 2) = log( x +
2) = log( x +  2) )
2) )
Differentiating w.r.to x.,
y.1/ 2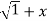 2 .2x+
2 .2x+ 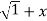 2. Y1.
2. Y1.
=(1+x ) y +xy = 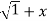 . 1/x
. 1/x 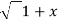 2 .
2 . 2) +x/
2) +x/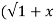 2 =1
2 =1
Statement:
If F(x) = 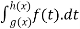 ,then
,then
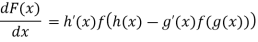
Proof:
Let P(t) = 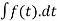
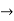 F(x) =
F(x) = 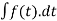
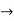 F(x) =
F(x) = 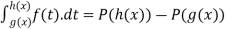
 = P’(h(x))h’(x) – P’(g(x))g’(x)
= P’(h(x))h’(x) – P’(g(x))g’(x)
= f(h(x)).h’(x)-f(g(x))g’(x)
Exercise 19:
Sove the following using lebinitz rule:
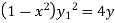
Solution:
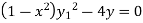

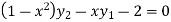
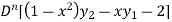 =0
=0
Exercise 20:
Find the envelope of the family of the ellipses defined by the equation
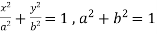
Solution:
The equation for the given family of curves can be writeen as
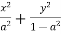 =1…..(1)
=1…..(1)
Where the semi axis a is the parameter and 0<a<1
Differentiating eq(1) w.r.to a is
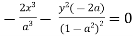
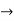
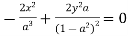
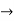
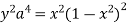
Take the square root of both sides of the equation:
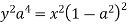
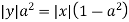
Express  from the last equation
from the last equation
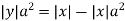


Substituting in the eq(1) we get
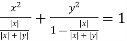
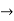
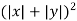 =1
=1
=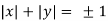
Exercise 21:
Find the evolute for the following parabola y=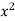
Solution:
For evoluting the parabola we have the following formulae,
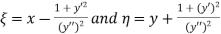
Substituting the given function we get
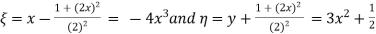
By eliminating the x in 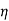 we getx =
we getx = 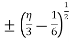
Substituting in 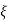 we get
we get 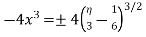
Therefore the required answer is 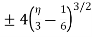
Exercise 22:
For a given curve convert the point (2, ) from polar to Cartesian form
) from polar to Cartesian form
Solution:
r=2 and 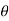 =
=  we have,
we have,
x = rcos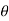 and y= rsin
and y= rsin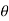
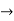 x= 2.cos
x= 2.cos = 2.1/2 = 1
= 2.1/2 = 1
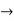 y = 2.sin
y = 2.sin = 2.
= 2.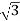 /2 =
/2 = 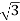
Therefore the required Cartesian point is (1,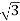 ).
).
Reference Books-
1.E. Kreyszig, Advanced Engineering Mathematics, John Wiley & Sons, 2005.
2.Peter V. O’Neil, Advanced Engineering Mathematics, Thomson (Cengage) Learning, 2007.
3.Maurice D. Weir, Joel Hass, Frank R. Giordano, Thomas, Calculus, Eleventh Edition,Pearson.
4.D. Poole, Linear Algebra: A Modern Introduction, 2nd Edition, Brooks/Cole, 2005.
5.Veerarajan T., Engineering Mathematics for the first year, Tata McGraw-Hill, New Delhi, 2008.
6.Ray Wylie C and Louis C Barret, Advanced Engineering Mathematics, Tata Mc-Graw-Hill, Sixth Edition.
7.P. Sivaramakrishna Das and C. Vijayakumari, Engineering Mathematics, 1st Edition, PearsonIndia Education Services Pvt. Ltd
8. Advanced Engineering Mathematics. Chandrika Prasad, Reena Garg, 2018.
9. Engineering Mathematics – I. Reena Garg, 2018.
