Unit – 2
Continuum & Free Molecular Flows
Continuum
- A continuous distribution of matter with no voids or empty spaces is called as continuum. For mechanical analysis, a fluid is considered to be continuum. e.g., water flowing through pipes, channel.
- Continuum is based on assumption that fluid is continuous. That is the properties such as density, pressure, temperature and velocity are taken to be well defined at infinitely small points and are assumed to vary continuously from one point to another. Air is considered as a Continuum.
- The mean-free-path-of atmospheric air is about 5 - 7.5 x 10-6 cm but these molecular spacing increases even under lower pressure, and the air no longer remains a continuum.
Key Takeaways:
A continuous distribution of matter with no voids or empty spaces is called as continuum. For mechanical analysis, a fluid is considered to be continuum. e.g., water flowing through pipes, channel.
Free molecular flows
- In some cases, the continuum theory is inapplicable. Such conditions exist when the distance between molecules, or, more precisely, the mean free path that they take between collisions with other molecules, is comparable to some physical dimension of the flow channel's container, d (
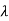 /d -1).
/d -1). - The controlling non-dimensional parameter for continuum prediction is the Knudsen number, which is defined as the ratio of the mean free path to the object's characteristic length. In this context, mean free path refers to the average distance travelled by a molecule between two sequential collisions with other molecules.
- For most of the relations or governing equations, the derived Knudsen number should be close to zero or less than 0.3 for continuum to hold
- The use of governing equations in their standard form remains intact at the first critical value of Knudsen number (0.3), but the nature of boundary conditions changes due to the presence of velocity and temperature slip on the wall.
- This occurs most frequently when the gas density is low (leading to a high mean free path) and the gas interacts with solid surfaces that have a small-scale structure, such as a porous solid or a capillary tube. In such cases, the gas molecules may interact with the solid surface as frequently as they do with other molecules, resulting in a transition regime. As a result, for the Knudsen number range of 0.3 to 1, commonly known as the transitional regime, slip wall boundary conditions should be applied in addition to the conventional governing equations based on the continuum assumption.
- When the density of the gas is reduced further, molecule-to-wall collisions entirely dominate the processes, and the free-molecule or Knudsen regime is reached when
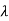 /d >> 1. The Knudsen Number (Kn) is the ratio
/d >> 1. The Knudsen Number (Kn) is the ratio 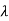 /d. This flow is independent of the gas's viscosity and density, and it is proportional to the third power of the radius of the tube, as opposed to viscous flow, which is proportional to the fourth power.
/d. This flow is independent of the gas's viscosity and density, and it is proportional to the third power of the radius of the tube, as opposed to viscous flow, which is proportional to the fourth power. - The presence of free molecular flow can be guaranteed if the Knudsen number exceeds 1. If the Knudsen number exceeds its second critical value, kinetic theory of gases and related equations are often mandated. This state persists beyond 150 km from the earth's surface, where air density is extremely low.
Key Takeaways:
- The Knudsen Number (Kn) is the ratio
 /d. That is the ratio of the mean free path to the object's characteristic length
/d. That is the ratio of the mean free path to the object's characteristic length - Free molecular flow occurs when mean free path of fluid is greater than dimension of chambers in which it is flowing
- If Kn < 0.3 continuum assumption can be applied
- If 0.3 < Kn < 1: transition regime
- If Kn >1: free-molecule or Knudsen regime
Steady flow
- The type of flow in which the fluid characteristics like velocity, pressure, density, etc. at a point do not change with time is called steady flow.
- Example: Flow through a prismatic or non-prismatic conduct at a constant flow rate Q m3/s is steady.
- Mathematically,
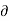 u/
u/ 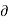 t = 0, w/ t = 0, p/ t = 0, rho / t = 0
t = 0, w/ t = 0, p/ t = 0, rho / t = 0
Unsteady flow
- It is that type of flow in which the velocity, pressure or density at a point change w.r.t. Time.
- E.g.: the flow in a pipe whose value is being opened or closed gradually.
- Mathematically,
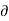 u/
u/ 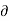 t not = to 0, w/ t not = to 0, p/ t not = to 0,
t not = to 0, w/ t not = to 0, p/ t not = to 0, 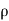 / t not = to 0
/ t not = to 0
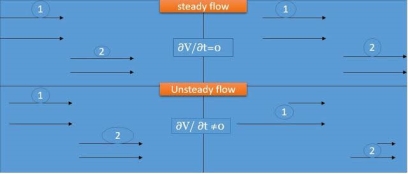
Fig: Steady and Unsteady flow
Key takeaways:
The type of flow in which the fluid characteristics like velocity, pressure, density, etc. at a point do not change with time is called steady flow.
It is that type of flow in which the velocity, pressure or density at a point change w.r.t. Time.
Uniform flow –
- The type of flow, in which the velocity at any given time does not change with respect to space is called uniform flow.
- E.g.: Flow through a straight prismatic conduit.
- Mathematically,
 V /
V / 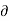 s = 0 when t = constant
s = 0 when t = constant
Non-uniform flow –
- It is that type of flow in which the velocity at any given time changes with respect to space.
- E.g.: Flow through non-prismatic conduit.
- Mathematically,
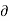 V/
V/ 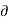 s not = to 0 when t = constant
s not = to 0 when t = constant
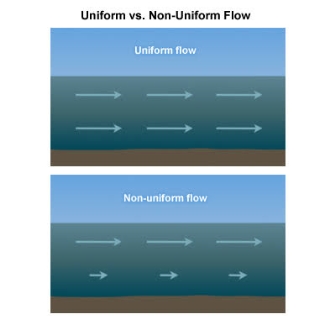
Fig: Uniform and non-uniform flow
Key takeaways:
The type of flow, in which the velocity at any given time does not change with respect to space is called uniform flow.
It is that type of flow in which the velocity at any given time changes with respect to space.
Laminar Flow –
- A Laminar flow is one in which paths taken by the individual particles do not cross one another and move along well-defined path.
- E.g.: Flow of blood in veins and arteries.
Turbulent Flow –
- A turbulent flow is that flow in which fluid particles move in a zig zag way.
- E.g.: High velocity flows in conduit of large size.

Fig: Laminar and turbulent flow
Key takeaways:
A Laminar flow is one in which paths taken by the individual particles do not cross one another and moves along well-defined path.
A turbulent flow is that flow in which fluid particles move in a zig zag way.
Rotational Flow –
- A flow said to be rotational if the fluid particles while moving in the direction of flow rotate about their mass centers.
- E.g.; Motion of liquid in a rotating tank.
Irrotational flow –
- A flow said to be rotational if the fluid particles while moving in the direction of flow do not rotate about their mass centers.
- E.g.: Flow above a drain hole of a stationary tank or a water basin.
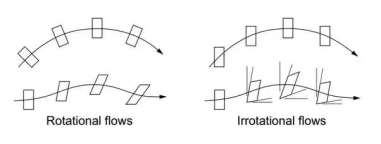
Fig: Rotational and irrotational flow
Key takeaways:
A flow said to be rotational if the fluid particles while moving in the direction of flow rotate about their mass centers.
A flow said to be rotational if the fluid particles while moving in the direction of flow do not rotate about their mass centers.
Compressible Flow –
- It is that type of Flow in Which the density () of the fluid changes from point to point.
- E.g.: Flow of gases through orifices, nozzles, gas turbines, etc.
- Mathematically,
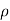 not = to constant
not = to constant
Incompressible Flow –
- It is that type of flow in which density is constant for the fluid flow. Liquids are generally considered flowing incompressible.
- E.g.: subsonic aerodynamics.
- Mathematically,
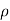 = constant
= constant

Fig: Compressible and incompressible flow
Key takeaways:
It is that type of Flow in Which the density () of the fluid changes from point to point.
It is that type of flow in which density is constant for the fluid flow. Liquids are generally considered flowing incompressible
Sonic Flow: The flow for which Mach number is equal to unity.
Subsonic Flow: For this, Mach number ‘M’ is in between range 0.4 to 1.0
Supersonic Flow: Mach number for this flow is always greater than unity but less than six.
Subcritical Flow:
- When Froude number is less than one or V>
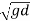 ,the flow is said to be subcritical flow or tranquil or streaming flow.
,the flow is said to be subcritical flow or tranquil or streaming flow.
Fr <1
Critical flow:
- When Froude number is less than one or V=
 ,the flow is said to be Critical flow.
,the flow is said to be Critical flow.
Fr =1
Supercritical Flow:
- When the Froude number is greater than one or V>
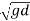 , the flow is said to be super critical flow or Rapid flow or Shooting flow.
, the flow is said to be super critical flow or Rapid flow or Shooting flow.
Fr >1
One dimensional flow –
- It is that type of flow in which the flow parameter such as velocity is a function of time and one space coordinate.
- E.g.: Flow in a pipe where average flow parameters are considered for analysis.
- Mathematically, u = f(x), v = 0 & w = 0
Two-dimensional flow –
- The flow in which the velocity is a function of time and two rectangular space coordinates is called two-dimensional flow.
- E.g.: Flow between parallel plates of infinite extent.
- Mathematically, u = f1(x, y) v = f2(x, y) & w = 0
Three-dimensional flow –
- It is that type of flow in which the velocity is a function of time and three mutually perpendicular directions.
- E.g.: Flow in a converging or diverging pipe or channel.
- Mathematically, u = f1(x, y, z) v = f2(x, y, z) & w = f3(x, y, z)
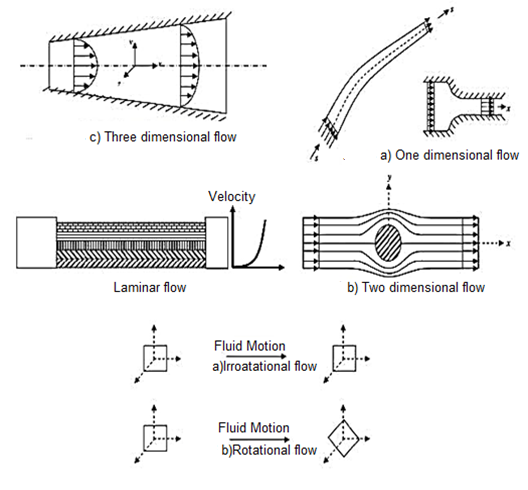
Fig: One two- and three-dimensional flow
Key takeaways:
The Types of flow can be classified on basis of their physical and dynamic properties and their states.
A stream line is an imaginary curve created through a flowing fluid in such a way that the tangent to it at any location reveals the direction of the flow's instantaneous velocity (V) at that place.
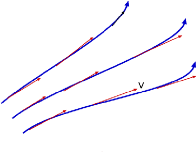
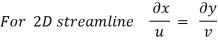
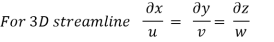
Because velocity is always tangential to the stream line, there is no component of velocity perpendicular to the stream line; thus, any discharge trapped between two stream lines remains trapped there; thus, as the gap between stream lines increases, velocity decreases; and as the gap decreases, velocity increases.
Stagnation point: In a fluid flow system, the point at which the velocity of flow becomes zero is referred to as the stagnation point.
Path Line: The actual path taken by every individual fluid particle over a given time period is referred to as the path line, and path line is a lagrangian concept. These are the actual lines, not fictitious ones. These lines may intersect.
Streak Line: It is the location of all fluid particles that have passed through the same point at the same time.
Key Takeaway
- Physically, these three lines are distinct, but mathematically, they may be the same for continuous flow. Each line tells the following
- Streamline: Motion Direction (velocity).
- Pathline: The motion of a specific fluid particle.
- Streakline: Identifies the location of various fluid particles.
Examples:
Q.1 The velocity of a flow is given by v = -x i + 2y j + (5 - 2) k. Derive the equation of streamline passing through a point (2, 1, 1).
Soln.:
u = -x, v = 2y and w = 5-z
The streamline,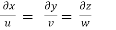 put the value of u, v and w
put the value of u, v and w
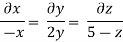
Consider,
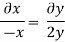
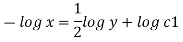
Stream line passing through x=2, y=1, z= 1


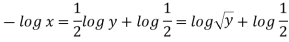

Now consider,
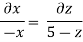
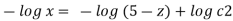
Stream line passing through x=2, z=1
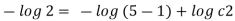
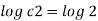
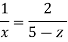
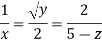
Q.2 For the three-dimensional flow, the velocity distribution is given by u-x, v-4-2y, w z-2. What is the stream line equation passing through (1.-2, 3)?
Soln.:
The streamline,
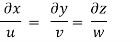
Put the value of u, v and w
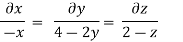
Consider 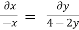
By integrating
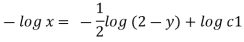
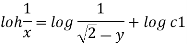
Stream line passing through x=1 y= =-2
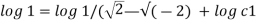
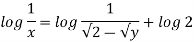

Now considering
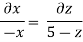
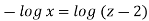
From equation

Q.3 The velocity component in a steady flow is u=2kx, v= 2ky, w = - 4kz. What is the through the point (1, 0, 1).
Soln.:
The streamline,
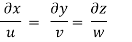
Put the value of u, v and w
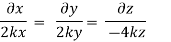
Now considering
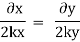
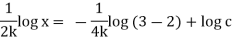
Stream line passing through x = 1, z=3,
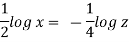
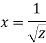
This is the equation of streamline passing through the point (1,0,1)
Q. 4 The velocity field for a two-dimensional flow is given by V= 4x³i-12x²yj. What is the equation of streamlines?
Soln.:
Velocity vector v = 4x'i-12x²yj
Velocity component u = 4x², v = -12x²y
Stream line
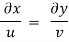
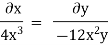
By integrating,
3 log x = -log y + log C
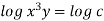
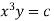
The curve defined by x³y = C₁, C₂, C, ...etc.
Key takeaways:
A streamline may be defined on as an imaginary line within the flow so that the tangent at any point on it indicates the velocity at that point.
An important concept in aerodynamics research touches on the concept of simple methods. The arrangement is the process followed by the weightless particles as they flow and flow.
One dimensional
- The continuity equation is based on the principle of conservation of mass. It states as follows
- If no fluid is added or removed from the pipe in any length then the mass passing across different sections shall be same.
- Consider two cross-sections of a pipe as shown in fig.
Let, A1&A2 = Areas of the pipe at section 1-1 & section 2-2 respectively.
V1 & V2 = Velocities of the fluid at section 1-1 & section 2-2 respectively.
1 &2 = Densities of the fluid at section 1-1 & section 2-2 respectively.
Total quantity of fluid passing through the section 1-1 = 1A1V1
Total quantity of fluid passing through the section 2-2 = 2A2V2
- From the law of conservation of matter
1 A1 V1 = 2 A2 V2
- In case of incompressible fluids 1 =2
A1 V1 = A2 V2
Three dimensional
- Considers a fluid element (control volume)- parallelepiped with sides dx, dy and dz as shown in fig.
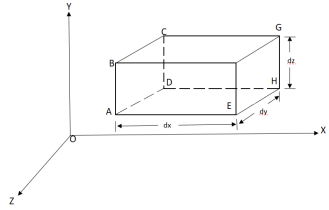
Fig: Continuity equation
Let, 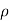 = Mass density of the fluid at a particular instant
= Mass density of the fluid at a particular instant
u, v, w= components of velocity of flow entering the three faces of the parallelepiped.
Rate of Mass of fluid entering the face ABCD
=  X velocity in x-direction X area of ABCD
X velocity in x-direction X area of ABCD
=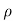 u dy dz
u dy dz
Rate of Mass of fluid leaving the lace FEGH
=  u dy dz +
u dy dz + 
:. Mass accelerated per unit time, due to flow in x-direction
= 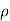 u dy dz – [
u dy dz – [ u+
u+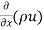 dx] dydz
dx] dydz
= - -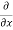 (
(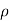 u) dx dy dz
u) dx dy dz
Similarly, the gain in fluid mass per unit time in the parallelepiped due to flow in Y and Z- direction.
= 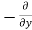 (
(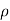 v) d x d y d z ……… (in Y- direction)
v) d x d y d z ……… (in Y- direction)
= 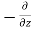 (
(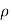 w) d x d y d z ……… (in Z- direction)
w) d x d y d z ……… (in Z- direction)
The, total gain in fluid mass per unit for fluid along three co-ordinate axes
= - [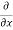 (
(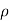 u) +
u) +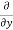 (
(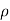 v) +
v) + 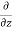 (
(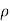 w)] dx dy dz …………1
w)] dx dy dz …………1
Rate of change of mass of the parallelepiped (control volume)
=  (
(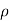 d x, d y d z) …………………... 2
d x, d y d z) …………………... 2
From Equation 1& 2
- [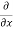 (
(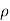 u) +
u) +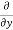 (
(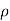 v) +
v) +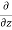 (
(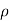 w)] dx dy dz =
w)] dx dy dz = 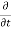 (
(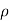 dx dy dz)
dx dy dz)
Simplification and rearrangement of teams would reduce the above expression to
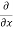 (
(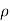 u) +
u) + 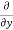 (
(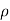 v) +
v) + 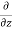 (
(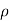 w) +
w) + 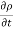 =0
=0
This eq. Is the general equation of continuity in three dimension and is applicable to any type of flow and for any fluid whether compressible as incompressible
For steady flow (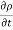 =0) incompressible fluids (
=0) incompressible fluids (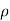 = constant) the equation reduces to
= constant) the equation reduces to
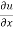 +
+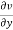 +
+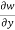 =0
=0
Examples:
Q.1 The velocity components for a two-dimensional incompressible flow is given by
1) u = 4 xy + y². v = 6 xy + 3x
2) 
Check whether the flow satisfies continuity?
Soln.:
(i) u = 4 xy + y², v = 6 xy + 3x
Differentiating
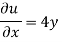
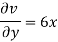
For two-dimensional flow continuous equation is
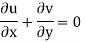
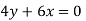
Velocity components does not satisfy the continuity equation
Ii) 
Differentiating

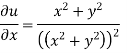
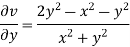
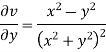
For two-dimensional flow continuous equation is
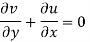
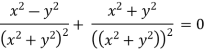
Satisfy the continuous equation.
Q.2 The velocity components for a three-dimensional incompressible flow is given by: 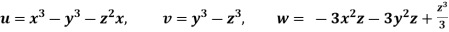 Check whether the flow satisfies continuity?
Check whether the flow satisfies continuity?
Soln.:
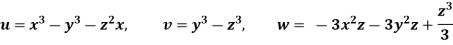
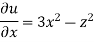
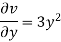
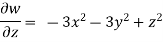
Foe three-dimensional equation continuous equation is
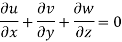
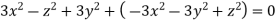
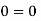
The flow is satisfied.
Q.3 The velocity field is given by 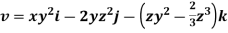 check whether the flow satisfies continuity?
check whether the flow satisfies continuity?
Soln.:
Velocity field
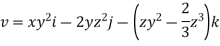
Velocity component
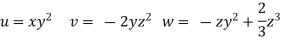
For three-dimensional flow
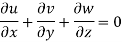
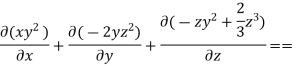
Steady incompressible fluid flow is possible.
Key takeaways
If no fluid is added or removed from the pipe in any length then the mass passing across different sections shall be same.
One dimensional
Two dimensional
Three dimensional
- In rotational motion, circulation is very useful concept.
- Circulation around a closed curve C is define as the integrate of the tangential component of the velocity taken around a closed curve C, taken positive in anticlockwise direction. The flow along a closed curve called as circulation.
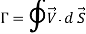
- Vorticity is 2 times of angular velocity and if it is zero flow is irrotational
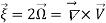
Circulation= Vorticiy 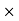 Area
Area
- E.g., Flow in eddies and vortices
- It is defined as the scalar function of space and time such that its partial derivative with respect to any direction gives the velocity component at right angles to that direction.
- It is denoted by Ψ (psi) and defined only for two-dimensional flow.
- Mathematically, for ready flow it is defined as Ψ = f (x, y) such that
 Ψ /
Ψ / 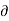 x= v
x= v
And 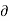 Ψ /
Ψ /  y = -u
y = -u
Examples:
Q.1 A stream function is given by 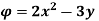 check if the flow is rotational and satisfies continuity equation
check if the flow is rotational and satisfies continuity equation
Soln.:
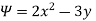
By definition
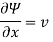
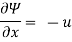
Velocity
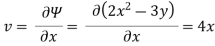
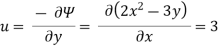
1) Irritational flow
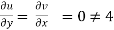
2) Continuity equation
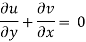
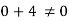
The flow is not continuous.
Q.2 Determine whether the following specified flows are rotational or otherwise. Determine the expression for the velocity potential in case of irrotational flow
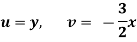
Soln.:
For rotational flow
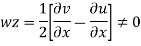
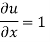
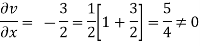
Flow is rotational.
Key takeaways:
It is defined as the scalar function of space and time such that its partial derivative with respect to any direction gives the velocity component at right angles to that direction.
- The velocity potential is defined as scaler function of space and time such that its negative derivative with respect to any directions gives the fluid velocity in that direction.
- It is denoted by Ø (phi).
- Thus, mathematically the velocity potential is defined as
Ø = f (x, y, z, t)
And Ø = f (x, y, z)
u = - 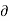 Ø /
Ø / 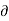 x
x
v = - 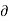 Ø /
Ø / 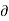 y
y
w = - 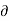 Ø /
Ø / 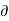 z
z
Where u, v and w are the components of velocity in the x, y and z directions respectively.
- The negative sign signifies that Ø decreases with an increase in the values of x, y and z. In other words, it indicates that the flow is always in the direction of decreasing Ø.
Examples
Q.1 The velocity potential function is given by an expression 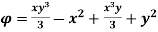
1) Find the velocity components in x and y direction
2) Show that  represents a possible case of flow
represents a possible case of flow
Soln.:
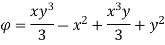
Case I) the partial derivation of 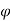 w.r.t x and y are
w.r.t x and y are
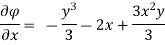
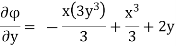
The velocity components u and v
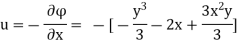
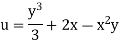

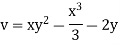
Case II) The value of 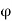 represents a possible case of flow if it satisfies the laplace equation
represents a possible case of flow if it satisfies the laplace equation
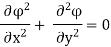
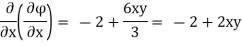
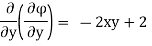

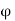 Represents possible case of flow.
Represents possible case of flow.
Q.2 The velocity potential function for a two-dimensional flow is 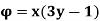 at a point P (4, 5). Determine the velocity.
at a point P (4, 5). Determine the velocity.
Soln.:
Velocity potential
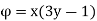
Differential w.r.t x
Hence
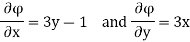
By definition of 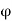

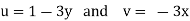
Velocity at P (4, 5)
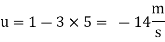
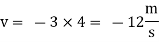
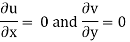
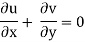
Flow is continuous
Key takeaways:
The velocity potential is defined as scalar function of space and time such that its negative derivative with respect to any directions gives the fluid velocity in that direction.
- When a large number of physical variables are involved Rayleigh’s method of dimensional analysis becomes increasingly laborious and cumbersome.
- Buckingham’s method is an improvement over the Rayleigh’s method.
- Buckingham’s designated the dimensionless group by the letter Π. It is therefore often called Buckingham Π-Method.
- The Buckingham’s Π-Method states as follows:
“If there are n variables in a dimensionally homogeneous equation and if these variables contain fundamental dimensions (such as M, L, T, etc.) then the variables are arranged into (n-m) dimensionless terms.
- These dimensionless terms are called Π– terms.”
Mathematically, if any variable X1, depends on independent variables, X2, X3, X4,…… Xn; the functional equation may be written as
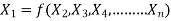 -------- 1
-------- 1
Equation 1 can also be written as
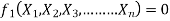 -------- 2
-------- 2
It is dimensionally homogeneous equation and contains n variables.
If there are m fundamental dimensions, then according to Buckingham’s Π – theorem, it can be written in terms of number of Π – terms in which number of Π terms is equal to (n-m).
Hence equation 2 becomes as
 --------3
--------3
Each dimensionless 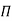 – term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variable.
– term is formed by combining m variables out of the total n variables with one of the remaining (n-m) variable.
These m variables which appear repeated in each of 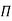 – terms are consequently called repeating variables and are chosen from among the variables such that they together involve all the fundamental dimensions and they themselves do not form a dimensionless parameter.
– terms are consequently called repeating variables and are chosen from among the variables such that they together involve all the fundamental dimensions and they themselves do not form a dimensionless parameter.
Let in the above case X2, X3 and X4 are the repeating variables if the fundamental dimensions m (M, L, T) = 3, then each term is written as:
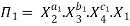
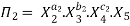
.
.
.
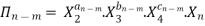 -------- 4
-------- 4
Where a1, b1, c1, a2, b2, c2 etc. are the constants, which are determined by considering dimensional homogeneity. These values are substituted in equation 4 and values of  are obtained. These values of Π’s are substituted in equation 3.
are obtained. These values of Π’s are substituted in equation 3.
The final general equation for the phenomenon may then be obtained by expressing anyone of the Π – terms as a function of the other as:
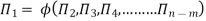
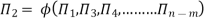
Key takeaways:
The final general equation for the phenomenon may then be obtained by expressing anyone of the Π – terms as a function of the other as:

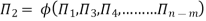
The ratio of two forces is called as dimensionless parameter or number. The following are the important dimensionless numbers used in fluid mechanics.
- Reynold's number
- Froude's number
- Weber's number
- Euler's number
- Mach's number.
Reynold’s Number:
The ratio of inertia force to the viscous force is called as Reynold's number. It is denoted by Re.
=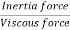
=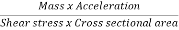
=
=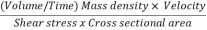
=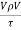 =
=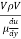
=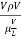 =
=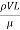 =
= =
=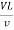 ∵v=
∵v=
Applications of Reynolds number:
Motion of completely submerged bodies like submarine, aeroplanes and automatic with low velocity, Incompressible flow through pipes, flow through low-speed turbo machine in which viscous forces are predominant.
Froude's Number:
The square root of the ratio of inertia force and gravitational force is called Froude's number. It is denoted by F
∴Fr=
=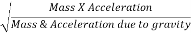
=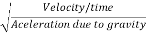
=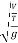 ∵V=
∵V= =T=
=T=
=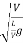 =
=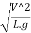 =
=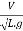
Application:
Open hydraulic structure such as spillways, wiers, open channel flow, sluices etc. in which force due to gravity are predominant.
Weber's Number
The square root of the ratio of the inertia force to the surface tension force. It is denoted by We.
We= =
=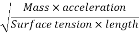
=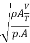 ∵A/T=Q=V.A
∵A/T=Q=V.A
=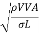 ∵A=L2=
∵A=L2=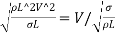
Application:
Capillary movement of water in soils, flow of blood in veins and arteries where the surface tension effects are predominant.
Euler's Number:
The square root of the ratio of inertia force to the pressure force is called as Euler's ratio.
= =
=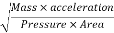
=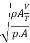 =
=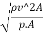 =
=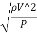
=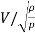 ∵A/T=Q=V.A
∵A/T=Q=V.A
Application:
In cavitation study where pressure force is predominant.
Mach's Number or Cauchy's Number:
The square root of the ratio of inertia force to the elastic force is called as Mach's number or Cauchy's number.
MN = =
=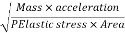
=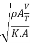 =
=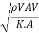 =
=
=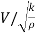 ∵A/T=Q=V.A
∵A/T=Q=V.A
Application:
In compressible fluid flow, problems at high speed such as high velocity flow in pipes, water hammer, motion of high-speed objects like aeroplane, projectile and missiles. Where the elastic force (compressibility effect) is predominant.
Key Takeaways:
The ratio of two forces is called as dimensionless parameter or number. The following are the important dimensionless numbers used in fluid mechanics.
- Reynold's number
- Froude's number
- Weber's number
- Euler's number
- Mach's number.
References:
1. Introduction to fluid mechanics and Fluid machines by S.K Som, Gautam Biswas, S Chakraborty.
2. Fluid mechanics and machines by R.K Bansal.
3. F. M. White, Fluid Mechanics, 6th Ed., Tata McGraw-Hill, 2008.
4. Fluid Mechanics and Its Applications by V.K. Gupta et.al.
5. Fluid Mechanics by Yunus Cengel.