Unit – 4

Introduction To Hydrodynamic Thrust of Jet

4.1 Introduction to hydrodynamic thrust of jet on a fixed and moving surface

The liquid emerges as a jet from the output of a nozzle attached to a pipe carrying the liquid under pressure. A jet is a stream of fluid that is projected into the surrounding medium from a nozzle, aperture, or orifice. Jets have the ability to travel large distances without expending their energy. When compared to the surrounding fluid medium, jet fluid has a higher momentum. When the surrounding medium is supposed to be made up of the same fluid as the jet and this fluid has a viscosity, entrainment occurs, and the surrounding fluid is carried along with the jet.

Force exerted by the jet on a stationary vertical plate

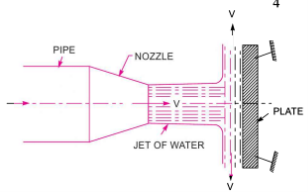
Consider a jet of water coming out from a jet of water from the nozzle collides with the vertical plate.

V = jet velocity, d = jet diameter, a = x – section area of the jet

The force that the jet exerts on the plate in the jet's direction.

Fx denotes the rate of change of momentum in the force's direction.

(Initial momentum – final momentum)/time = rate of change of momentum in the direction of force

After striking the plate, the jet will move along it. However, the plate is perpendicular to the jet. As a result, the jet will be deflected 90 degrees after impact. As a result, after striking, the component of the jet's velocity in the direction of the jet will be zero.

The force applied to the plate by the jet in the direction of the jet.

F= Rate of change of momentum in the direction of force

F= (Initial momentum - Final momentum)/Time

F= (Mass x Initial velocity - Mass x Final velocity)/Time

F= [Mass/ Time]x[Initial velocity - Final velocity]

F= (Mass/sec) x (velocity of jet before striking - velocity of jet after striking)

F= aV[V - 0]

F= 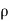aV²…………………………………………………..( mass/sec = x aV)

We used initial velocity minus final velocity instead of final velocity minus initial velocity to derive the above equation. 

When calculating the force put on the jet, the end velocity is subtracted from the initial velocity. 

When calculating the force applied by the jet on the plate, however, initial velocity minus final velocity is used. When the density (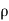) is expressed in SI units (kg/m3), the force (F) is expressed in Newtons (N). In S.I. Units, the value of p for water is 1000 kg/m3

Q. Find the force exerted by a jet of water of diameter 75 mm on a stationary flat plate, when the jet strikes the plate normally with velocity of 20 m/s.

Solution

Given:

Diameter of jet, d = 75 mm = 0.075 m

Area a= (π/ 4) d²= (π/ 4) (0.075)² = 0.004417 m² 4

Velocity of jet, V = 20 m/s.

The force exerted by the jet of water on a stationary vertical plate is given by equation as

F = 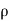av² where = 1000 kg/m³

F = 1000 x .004417 x 20² N = 1766.8 N.

Q. Water is flowing through a pipe at the end of which a nozzle is fitted. The diameter of the nozzle is 50 mm and the head of water at the centre nozzle is 80 m. Find the force exerted by the jet of water on a fixed vertical plate. The co-efficient of velocity is given as 0.95.

Solution

Given:

Diameter of nozzle, d = 50mm = 0.05 m

Head of water, H = 80 m

Co-efficient of velocity, Cv = 0.95

Area of nozzle, a =(π/ 4) (0.05)² =0.0019634 m²

Theoretical velocity of jet of water is given as

Vth=√(2gH) = √(2x9.81x80) = 39.6181 m/s

Cv = Actual velocity Theoretical velocity

Actual velocity of jet of water, V = Cv x V = 0.95 × 39.6181 = 37.6372 m/s.

Force on a fixed vertical plate is given by equation

F =  av² = 1000 x .0019634 x 37.6372² (In S.I. Units for water = 1000 kg/m³)

= 2781.40 N = 2.7 kN.

Force of Jet Impinging on an Inclined Fixed Plate:

Let a jet of water, coming out from the nozzle, strikes an inclined flat plate as shown in

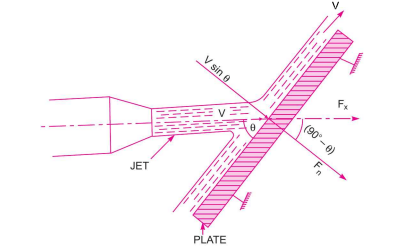
Let

V = Velocity of jet in the direction of x.

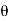= Angle between the jet and plate,

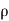= Area of cross-section of the jet.

Then mass of water striking is = x aV

If the plate is smooth and there is no energy loss owing to the impact of the jet, the jet will move over the plate with a velocity equal to its starting velocity, i.e., with a velocity V. Let's calculate the force applied by the jet on the plate in the normal to the plate direction. Let F be the symbol for this force.

Fn = mass of jet striking per second x [Initial velocity of jet before striking in the direction of n- Final velocity of jet after striking in the direction of n]

= aV [V sin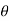 -0] = 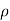aV² sin 0

This force can be resolved into two components, one in the direction of the jet and other perpendicular to the direction of flow. Then we have,

Fx =component of Fn in the direction of flow

= Fn cos(90° - 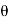) = Fn sin = 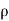a V² sin x sin 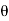(.. Fn, = 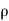av² sin )

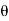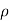= aV² sin²

Fy =component of Fn perpendicular to flow

= Fn sin (90° - 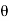) = Fn cos 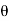= 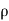aV² sin 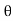cos.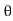

Q. A jet of water of diameter 50 mm strikes a fixed plate in such a way that the angle between the plate and the jet is 40°. The force exerted in the direction of the jet is 1471.5 N. Determine the rate of flow of water.

Solution

Given:

Diameter of jet, d = 50 mm = 0.05 m

Area, a= (π/ 4) (0.05)² = 0.001963 m²

Angle, 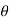= 40°

Force in the direction of jet, Fn = 1471.5 N

Force in the direction of jet is given by as Fn = 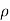av² sin²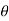

As the force is given in Newton, the value of 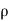should be taken equal to 1000 kg/m³

1471.5 =1000 x .001963 x V² x sin² 40°

V² = 1814.2827

V = 42.59m/s

Q Area x Velocity

= .001963 x 42.59= 0.08361 m³/s =83.61 liters/s.

Force Exerted by a Jet on Stationary Curved Plate

Case 1 Jet hitting at middle and plate in symmetrically 

Jet strikes onto the curved plate in the middle. As depicted in Fig., a jet of water impacts a fixed curved plate in the centre. If the plate is smooth and there is no energy loss owing to the jet's collision in the tangential direction of the curved plate, the jet returns with the same velocity after impacting it. The velocity at the plate's exit can be broken down into two halves, one parallel to the jet's path, and the other perpendicular to the jet's direction – Vcos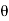 is the component of velocity in the direction of the jet. (-ve sign is taken as the velocity at outlet is in the opposite direction of the jet of water coming out from nozzle).

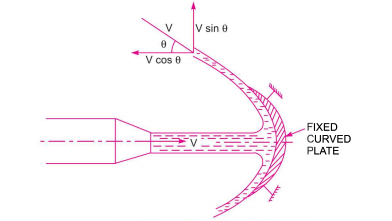
Component of velocity perpendicular to the jet= V sin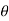

Force exerted by the jet in the direction of jet,

Fx = Mass per sec x [V₁x - V₂x],

Where V₁x is initial velocity in the direction of jet = V

V₂x is final velocity in the direction of jet= - Vcos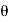

Fx = aV [V-(-V cos )]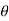

Fx = 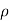aV [V + V cos ]

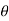Fx = 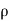aV² [1 + cos ]

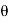Similarly,

Fy = Mass per sec x [V₁y – V2y]

Where V₁y is initial velocity in the direction of y =0

V₂y is final velocity in the direction of y = V sin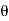

Fy = 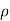aV [0-V sin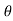]= - 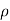aV² sin

-ve sign means that force is acting in the downward direction. In this case the angle of deflection of the jet = (180° - )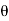

Case 2 Jet hitting tangentially and plate in symmetrically 

When the plate is symmetrical, the jet hits the curved plate tangentially at one end. Allow the jet to tangentially strike one end of the curved fixed plate. Assume that the curved plate is symmetrical on the x-axis. The tangents at the two ends of the plate will then make the same angle.

Fx = Mass per sec x [V₁x - V₂x],

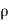= aV [V cos 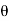-(-V cos )]

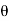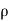= aV [V cos 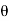+ V cos )]

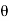=2 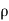aV² cos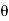

Fy = 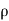aV [V₁y – V2y]

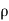= aV [V sin 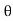-V sin]

=0

Case 3 Jet hitting tangentially and plate in unsymmetrically  

Let 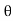be angle made by tangent at inlet tip from x axis and  be angle made by tangent at outlet tip from x axis

At inlet velocity component are

V₁x = Vcos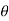

V₁y = V sin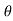

At outlet velocity component are

V₂x = Vcos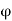 

V2y = V sin

Therefore, Forces exerted are

Fx = 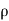aV [V cos 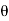+ V cos  ] = 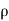aV²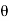[ cos +  cos  ]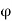 

Fy = 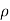aV [V sin -V sin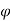] = 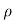aV²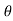[sin - sin] 

FORCE EXERTED BY A JET ON MOVING PLATES

The following cases of the moving plates will be considered

1. Flat vertical plate moving in the direction of the jet and away from the jet,

2. Inclined plate moving in the direction of the jet,

3.Force on curve plate when plate moving in direction of Jet

Force on Flat Vertical Plate Moving in the Direction of Jet.

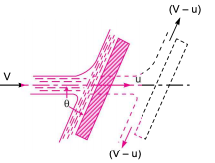
Fig. Shows a jet of water striking a flat vertical plate moving with a uniform velocity away from the jet.

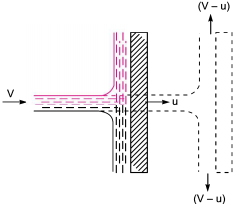
Let

V = Velocity of the jet (absolute),

a = Area of cross-section of the jet,

u= Velocity of the flat plate.

In this case, the jet does not strike the plate with a velocity V, but it strikes with a relative velocity, which is equal to the absolute velocity of jet of water minus the M velocity of the plate.

Hence relative velocity of the jet with respect to plate= (V-u)

Mass of water striking the plate per sec= 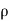x Area of jet x Velocity with which jet strikes the plate

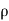= a x [V -u]

Force exerted by the jet on the moving plate in the direction of the jet.

Fx = Mass of water striking per sec x (Initial velocity with which water strikes - Final velocity]

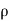= a(Vu) [(V-a)-0] ……………………. (Final velocity in the direction of jet is zero)

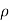= a(V-u)²

In this case, the work will be done by the jet on the plate, as plate is moving. For the stationary plates, the work done is zero.

Work done per second by the jet on the plate

= Force x (Distance in the direction of force/Time)

= Fx x u = 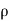a(V-u)² x u

In equation if the value of p for water is taken in S.I. Units (i.e. 1000 kg/m³), the work done will be in N m/s. Or watts

Q. A jet of water of diameter 10 cm strikes a flat plate normally with a velocity of 15 m/s. The plate is moving with a velocity of 6 m/s in the direction of the jet and away from the jet. Find:

(i) the force exerted by the jet on the plate (ii) work done by the jet on the plate per second.

Solution.

Given:

Diameter of the jet, d = 10 cm = 0.1 m

Area, a= (π/ 4) d² = (π/ 4) (0.1)² = .007854 m²

Velocity of jet, V = 15 m/s

Velocity of the plate, u = 6 m/s

(i) The force exerted by the jet on a moving flat vertical plate is given by equation

Fx = a (V-u)²= 1000 x .007854 x (15-6)² N = 636.17 N

(ii) Work done per second by the jet= Fx x u = 636.17 x 6 = 3817.02 Nm/s.

Force on the Inclined Plate Moving in the Direction of the Jet.

Let a jet of water strikes an inclined plate, which is moving with a uniform velocity in the direction of the jet as shown (V-u)

Let

V = Absolute velocity of jet of water,

u = Velocity of the plate in the direction of jet,

a = Cross-sectional area of jet, and

= Angle between jet and plate.

Relative velocity of jet of water = (V-u)

The velocity with which jet strikes = (V - u)

Mass of water striking per second

= a (V-u)

If the plate is smooth and loss of energy due to impact of the jet is assumed zero, the jet of water will leave the inclined plate with a velocity equal to (V-u).

The force exerted by the jet of water on the plate in the direction normal to the plate is given as

Fn = Mass striking per second x [Initial velocity in the normal direction with which jet strikes - Final velocity]

= a (V-u) [(V-u) sin 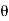-0] = a (V - u)² sin 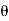...(17.13)

This normal force Fn is resolved into two components namely Fx and Fy in the direction of the jet and perpendicular to the direction of the jet respectively.

Fx = Fn sin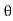 = 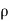a (V - u)² sin²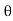

Fy = Fn cos 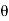= 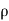a (V - u)² sin 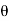cos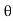

Work done per second by the jet on the plate= Fx × Distance per second in the direction of x

= Fx x u = 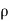a(V - u)² sin² x u  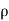  = a (V -  u)² u sin² 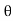 N m/s

Q. A nozzle of 50 mm diameter delivers a stream of water at 20 m/s perpendicular to a plate that moves away from the jet at 5 m/s. Find:

(i) the force on the plate, (ii) the work done, and(iii) the efficiency of jet.

Solution

Given:

Dia. Of jet, 50 mm = 0.05 m

Area, a = (π/ 4) (0.05)2 = 0.0019635 m²

Velocity of jet, V = 20 m/s. Velocity of plate, u = 5 m/s

(i) The force on the plate is given by equation as,

Fx = 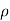a (V-u)²

=1000 x 0.0019635 x (20 - 5)² = 441.78 N. Ans.

(ii) The work done by the jet

= Fx = 441.78 x 5 = 2208.9 Nm/s. Ans.

(iii) The efficiency of the jet, n=Output of jet/Input of jet

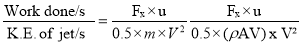
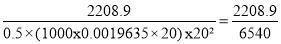
= 0.3377= 33.77%.

Force on curve plate when plate moving in direction of Jet

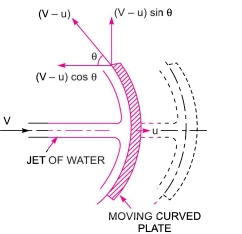
Component in direction of jet =-(V -u )cos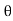 

-ve sign because direction of outlet component is in opposite direction of jet

Component in direction perpendicular of jet = (V -u)sin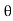 

Mass = 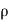 a multiplies by velocity in which jet strike

Mass = 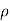a(V -u )

Force = mass per sec multiplied by [Initial – Final velocity]

FX =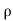 a(V -u )[(V -u )-(-(V -u )cos  )]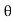

FX =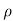 a(V -u )[(V -u )+ (V -u )cos  )]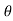

FX =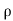 a(V -u )2[1+cos  ]

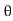Similarly

Fy=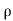 a(V -u )[(V -u )sin 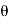- (V -u )cos 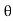 )] =0

Work done by jet on Plate

W = Fx x Distance Travelled per sec in direction of x

W=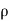 a(V -u )2[1+cos 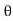 ] x u

Key Takeaway:

Jet Impact on	Fx	Fy
Fixed Plate	F= 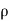aV²	-
Fixed Inclined Plane	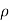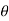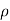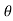aV² sin²	aV² sin cos .
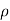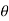
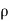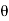Curved Plate middle	aV² [1 + cos ]	- aV² sin
Curved Plate Tangent Symmetrical	2 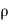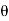aV² cos	0
Curved Plate Tangent unsymmetrical	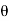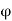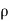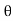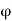aV²[ cos +  cos  ]	aV²[  sin - sin ]
Moving Plate	a(V-u)² x u	-
Moving Inclined Plate	a (V - u)² sin²	a (V - u)² sin cos
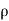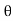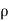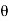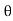Moving Curve Plate	a(V -u )2[1+cos   ]	0

4.2 Classification of turbines

Hydraulic turbines are classed based on the type of energy available at the turbine's intake, the direction of flow through the vanes, the head at the turbine's inlet, and the turbine's specific speed. As a result, the important classes of turbines are as follows:

1. According to the type of energy at inlet:

(a) Impulse turbine,

(b) Reaction turbine.

The turbine is known as an impulse turbine if the only energy available at the turbine's inlet is kinetic energy. From the turbine's inlet to outlet, the pressure is atmospheric as the water runs over the vanes. The turbine is known as an reaction turbine if both is kinetic energy and potential energy is available at the turbine's inlet.

2. According to the direction of flow through runner:

(a) Tangential flow turbine,

(b) Radial flow turbine,

(c) Axial flow turbine,

(d) Mixed flow turbine.

Tangential flow turbines are those in which the water flows along the tangent of the runner. Radial flow turbines are those in which the water flows in a radial direction via the runner. The turbine is known as an inward radial flow turbine if the water flows radially from outwards to inwards; on the other hand, the turbine is known as an outward radial flow turbine if the water flows radially from inside to outwards. A axial flow turbine is one in which the water flows through the runner in a direction parallel to the runner's axis of rotation. The turbine is called a mixed flow turbine when the water flows through the runner in a radial direction but leaves in a direction parallel to the runner's axis of rotation.

3. According to the head at the inlet of turbine:

(a) High head turbine,

(b) Medium head turbine,

(c) Low head turbine.

4. According to the specific speed of the turbine:

(a) Low specific speed turbine,

(c) High specific speed turbine.

(b) Medium specific speed turbine,

4.3 Impulse turbines, Constructional details, Velocity triangles, Power and efficiency calculations

Pelton Wheel:  

Pelton Wheel is a tangential flow impulse turbine. The water strikes the buckets along the tangent of the runner or wheel. It is used for the high heads more than 100m of water. These turbines have been used up to heads as high as 1600m.

Construction and working of Pelton Wheel

The water from the reservoir flows through the penstock to the nozzle which converts the pressure energy into kinetic energy. The resultant high velocity jet from nozzle strikes the buckets or vanes fitted at outer periphery of runner. The main components of the Pelton wheel are:

1. Nozzle and spear assembly

The needle spear is provided in the nozzle to regulate the water flow through the nozzle. Also, it provides smooth flow of water with negligible loss of energy. Spear is a conical needle which can be moved in axial direction by operating the wheel either manually or automatically. When the spear is moved in forward direction into the nozzle, it reduces the nozzle exit area, hence, the quantity of water flow striking the buckets is reduced. If the spear is moved backwards, it increases the flow rate of water. The nozzle converts the potential energy of water into kinetic energy before jet strikes the buckets. Pressure at exit of nozzle is reduced to atmospheric pressure.

2.     Runner and Buckets

The turbine rotor called runner is a circular disc fixed with buckets. It is provided with cylindrical boss and keyed to the supporting shaft in small thrust bearings. The runner carries cup-shaped buckets more that I5 in number which are mounted at equidistance around its periphery. The buckets are either cast integrally with the circular disc or these are bolted individually to the runner, it helps in easy replacement of buckets when worn out. Buckets are made of cast iron, cast steel, special steel or stainless steel with inner surface polished to reduce friction losses of water jet. Type of metal used for bucket depends on the head at turbine inlet. The shape of the bucket is of double Hemispherical cup or bowl. Each bowl of the bucket is separated by a wall called splitter or a ridge.

The shape and dimensions of a bucket are shown in figure given below. The commonly adopted dimensions of bucket are:

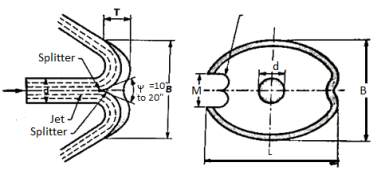
D = Diameter of jet

L = Length of height of bowl inside the rim = 2d to 3d

B= Width of bucket between the rim of bowl = 3d to 4d

T = Depth of bowl = 0.27 B to 0.32 B

M = Notch width = 1.1 d to 1.2 d

Splitter angle, ψ = 10° to 20°

The water strikes the bucket at the splitter which splits the water into two equal streams of the hemispherical bowl. The maximum force will be obtained when the jet is deflected through 180° into exact hemispherical bowl. However, in practice the jet is deflected through 160° to 170° (splitter angle ψ = 10° to 20°). It avoids striking the exit jet with the back of the succeeding bucket, thus exerting a retarding force on it. It would reduce the power output and the overall efficiency of turbine. This also avoids the splashing of water with a splitter. Pelton wheel is provided with two hemispherical cups since the splitter splits the jet into two equal streams, the axial component of each stream velocity is equal and opposite due to which the axial thrust on the shaft is negligible. Therefore, Pelton wheel needs very small thrust bearings. An undercut is provided and surface of spoons is raised so that water can be deflected back through the angle of 160° to 170° with the vertical without disturbing the incoming bucket.

3.     Casing

A casing does not have any hydraulic function to perform therefore it is not actually needed in case of impulse turbines because the runner runs under atmospheric pressure. However, a casing is provided to prevent the splashing of water and lead the water to tail race, and to safeguard the persons against accidents. It is made of cast iron in two halves.

4.     Braking Jet

Whenever the turbine is brought to rest, the nozzle is completely closed by pushing forward the spear. However, the runner continues to rotate due to its inertia for a considerable period of time till it comes to rest. In order to bring the runner to stop in a shortest time, a small nozzle is provided which issues the water jet and falls on the back of buckets. It acts as a hydraulic brake for reducing the speed of runner.

5.     Deflector

A deflector is provided which is hinged to the casing to deflect the jet of water away from striking the buckets in case the load on turbine suddenly reduces. It prevents the runner to attain unsafe speeds. A governing mechanism is also provided to control the speed of turbine according to variation in load which we will see in detail at later stage in this module.

Work Done and Efficiency of the Pelton Wheel

A jet of water strikes the bucket at its splitter. It splits the jet into two parts, each part of jet glides over the inner surface of the cup and leaves the outer tips of the bucket G-G1. The jet of water striking the splitter gets deflected through an angle (180 - Φ). Inlet and outlet velocity diagrams can be drawn as explained in theory of jet and it is shown in figure below for slow speed runner.

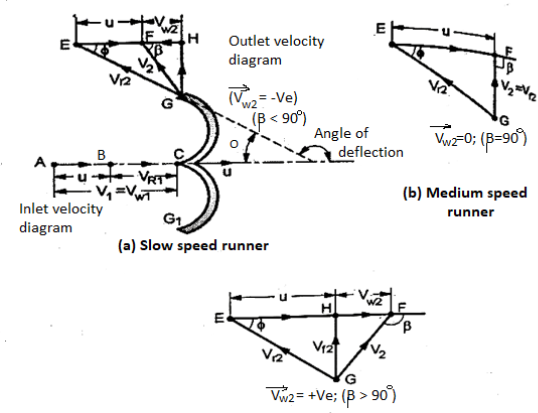
Figs (b) and (c) show the velocity diagram for medium speed and high-speed runners respectively,

Let d = diameter of jet in meters.

A = cross-sectional area of jet

Q = discharge rate, m3 /s

D = mean pitch diameter of runner,

N = speed of runner in r.p.m.

H = net head acting on Pelton wheel

Velocity of jet at inlet,

V1 = Cv √(2gH)       (1)

Where Cv is the coefficient of velocity of jet, its value varies from 0.91 to 0.99.

Blade velocity, u =πDN/60     (2)

Inlet velocity diagram

The Pelton wheel is a tangential flow turbine. The blade speed at inlet and outlet is same.

Therefore, u =u1 = u2; α = 0; Bucket inlet angle, θ = 0.

Therefore, inlet velocity diagram is a straight line where

Vr1 = V1 - u

Vw1 = V1      (i)

Outlet velocity diagram

Relative velocity at outlet Vr2 = K Vr1 where K is called friction factor. Its value is slightly less than unity and it is taken as one for a highly polished surface (neglecting friction).

Depending upon the speed of runner, various outlet velocity diagrams are drawn in Fig.

Vw2 = Vr2 cos Φ - u = (KVr1 cos Φ - u)  (ii)

Mass flow rate of water,

mf = ρ. Q= ρ AV1    (3)

1. Force exerted by jet in direction of motion, Fx

Fx = mf (Vw1 + Vw2)  (iii)

Considering slow speed runner when β < 90°, Vw2 is negative, therefore,

Fx = mf (Vw1 + Vw2)  (4)

b.    Work done by jet on runner per second, W

W = Fx u = mf (Vw1 + Vw2) u (5)

c.     Power developed, P

Here, Power developed is nothing but same as work done per second

P = W = mf (Vw1 + Vw2) u          (6)

d.    Hydraulic Efficiency, ηh

It is defined as the ratio of power delivered by runner to the power supplied at inlet. The power supplied at inlet is also called water power which is equal to kinetic energy of jet supplied to runner.

Kinetic energy supplied to jet per second = ½ mf V12

Hydraulic efficiency,

ηh = WD per second / KE supplied jet per second

= {mf (Vw1 + Vw2) u} / {½ mf V12}

= (2/V12) {(Vw1 + Vw2) u} (7)

Sometimes, the hydraulic efficiency is also called as bucket efficiency.

e.     Condition for maximum hydraulic efficiency, ηh

From the inlet velocity diagram

Vr1 = V1 - u

Vw1 = V1

From outlet velocity diagram

Vw2 = Vr2 cos Φ - u = (KVr1 cos Φ - u) = K (V1 - u) cos Φ - u

On substituting values of Vw1 and Vw2 in equation (7)

ηh = (2/V12) {(Vw1 + Vw2) u}

= (2/V12) {(V1 + K (V1 - u) cos Φ - u) u}

= (2/V12) {(V1 - u + K (V1 - u) cos Φ) u}

= (2/V12) (V1 - u) {1+ K cos Φ} u   (8)

The efficiency will be maximum when the differentiation of efficiency wrt blade velocity is equal to 0.

dηh / du = 0

D/du [(2/V12) (V1 - u) {1+ K cos Φ} u] = 0

(2/V12) {1+ K cos Φ} d / du [(V1 -u) u] = 0

d / du [(V1 -u) u] = 0

V1 - 2u = 0

V1 = 2u or u = V1 / 2    (9)

On substituting the above found value in (8),

We have,   ηhmax = (2/V12) (V1 - V1 / 2) {1+ K cos Φ} V1 / 2.

= [1 + cos Φ] / 2 (if k =1)  (10)

f.       Mechanical efficiency, ηm :

It is defined as the ratio of power available at turbine shaft to the power developed by runner.

Difference of these two powers is due to mechanical losses caused by friction between mating parts (e.g., in shaft and runner, bearings etc).

So, ηm = (power available at turbine shaft, Ps) / (power developed by runner, P) (11)

g.    Volumetric efficiency, ηv :

It is defined as the ratio of the volume of water actually striking the buckets to the volume of water issued by the jet. Hence,

Volumetric efficiency, ηv = Actual volume of water striking the bucket, Qa / Volume of water issued by the Jet, Q                                                                        (12)

Volumetric efficiency is less than 100% since some quantity of water misses the bucket and directly passes to tail race without doing any useful work. Volumetric efficiency for Pelton wheel ranges from 97% to 99%.

h.    Overall efficiency, ηo :

It is defined as the ratio of power available at turbine shaft to the power supplied by the water jet. Accordingly, ηo = Power available at turbine shaft, Ps / Power available the water jet, Pi               (13)

Pi = ρ g Q H

ηo = ηv x ηh x ηm      (14)

1. Plant efficiency, ηp :

If a generator of efficiency ηg is connected to turbine in hydro-electric plant. Then,

Plant efficiency, ηp = Power output from generator, Pg / Power supplied by the jet, Pi

4.4 Governing of Pelton wheel

It is generally done by oil pressure governors as shown in the figure below.

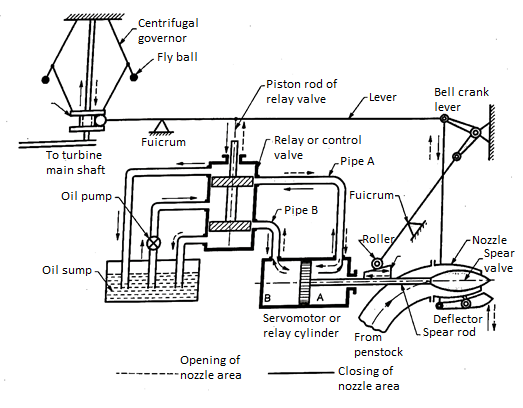
The major components of the governor mechanism are:

1. Oil pump and oil sump

System uses oil in servo motor or relay cylinder since the force required to actuate the spear valve would be enormous. For this reason, the system requires an oil sump to store the oil and an oil pump to regulate the oil supply in the mechanism. Oil pump is a positive displacement type of pump like gear pump or axial piston pump. Its function is to pressurize the oil.

2.     Relay or control valve

Relay valve is a spool valve having 5 ports. It is also called as control valve or distributor valve. It receives the pressurized oil from the oil pump which is diverted towards the ports connected to pipe A or pipe B. Through these pipes the oil is transferred to corresponding sides of double acting servo motor cylinder. Simultaneously, the oil will be returned from the servomotor from the opposite pipe to the sump.

3.     Servo Motor or relay cylinder

It is a double acting cylinder which acts as hydraulic actuator. It receives oil from relay valve say through pipe A. The piston of the cylinder will be displaced towards left, thus forcing the oil through the pipe B into the relay valve and finally to oil sump. It will simultaneously more the spear valve to the left and increase the area of flow through the nozzle.

4.     Spear valve

Spear valve controls the flow area of the nozzle. It is directly connected to the piston of relay cylinder.

5.     Governor and linkages

A centrifugal governor is used as the measuring element of the closed loop control system. It is driven by the turbine shaft through bevel gears. The sleeve of the governor is connected through linkages to relay valve. The movement of sleeve is transferred through the lever to more the piston rod of relay valve.

Working

Figure above shows the position when the turbine is running at normal speed.

Consider the case when the load on the generator increases, the speed of the generator and that turbine will decrease. Since the governor is driven by the turbine shaft, its speed will also decrease. As a consequence, the flyball of the governor will move inwards due to reduced centrifugal force on the balls. As a result, the sleeve of the governor will move downwards.

The downward motion of the sleeve will be transferred to the main lever through its fulcrum. It will cause the piston rod of the relay valve to move upwards and simultaneously the bell crank lever also moves upwards. The upward motion of piston rod of control valve causes pressurized oil to flow through the pipe A to the relay cylinder and exerts a force on face A on the piston of servomotor. It moves the piston to the left, thus the spear rod with its valve will also move towards the left. It will increase the nozzle area and the rate of flow of water to the turbine increases. Therefore, the input to turbine and consequently its speed increases. During this piston movement of servo motor to the left, oil held in the cylinder towards the face B is transferred through pipe B to the oil sump via the relay valve. When the speed of turbine is adjusted to normal speed, the system would return to its original position. Opposite will be action of the whole mechanism when the load on the generator decreases. The increase in speed of turbine and generator will increase the speed of the governor. The balls flyout and the sleeve moves upwards. It causes the piston rod of relay valve to move downwards, thus opening the valve towards pipe B. Pressurized oil flows into servo motor cylinder towards the face B and causes the spear to move towards right thus closing the nozzle area. The reduced discharge to turbine runner reduces the input, hence its speed. When the speed attained by the turbine is its normal speed, the governing mechanism will return to its original position.

4.5 Francis and Kaplan turbines

Francis Turbine

The inward flow reaction turbine having radial discharge at the outlet is known as Francis Turbine, after the name of J.B> Francis, an American engineer who is the beginning designed inward radial flow reaction type of turbine. In the modern Francis turbine, the water enters the runner of the turbine in the radial direction at the outlet and leaves in the axial direction at the inlet of the runners. Thus the modern Francis turbine is a mixed flow type turbine.

The velocity triangle at the inlet and outlet of the Francis turbine is drawn in the same way as in the case of the inward flow reaction turbine. As in the case of Francis turbine, the discharge is radial at the outlet, the velocity at whirl at the outlet (i.e., Vw2) will be zero. Hence the work done by water on the runner per second will be

=

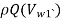
And work done per second per unit weight of water striking per second =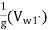

Hydraulic efficiency will be given by. nh =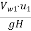

Components parts:

 Penstock: - It is a large-sized conduit that conveys water from the upstream of the dam to the turbine runner. A trash rack is provided at the inlet of the penstock to obstruct the entry of debris and other foreign matter.

 Scroll Casing: - The water from the penstock is conducted through the scroll casing and distributed around the stay ring and the complete circumference of the guide vane cascade. The decrease in area is in proportion to the decreasing volume of water to be handled and that ensures the velocity of water is constant along its path. The scroll casings are normally welded steel plate construction for a turbine at low, medium as well as high heads. The stay vanes are given a favorable hydraulic shape to conduct the water towards the guide vanes with minimum losses. The stay vanes also carry the axial forces inside the scroll casing. The scroll casing is provided with taps for pressure measurements, drain, air vent outlets, and a manhole.

 Guide Vanes: - A series of airfoil-shaped vanes, called the guide vanes or wicket gates, are arranged inside the casing to form some flow passages between the casing and the runner blades. The vanes are shaped according to the hydraulic design specification and given a smooth surface finish. The bearings of the guide vane shafts are lubricated with oil or grease. The guide vanes direct the water onto the runner at an angle appropriate to the design. It provides the degree of adaptability to the quantity of water to be admitted to the runner in the wake of load variations

 Runner and Runner Blades: - Runner is a rotor that has passages formed between crown and shroud in one direction and two consecutive blades on the other. These passages take water in at the outer periphery in the radially inward direction and discharge it in a direction parallel to the axis of the rotor. The driving force on the runner is both due to impulse and reaction effects. It may either be of cast steel or a welded construction where hot pressed plate blades are welded to the cast hub and ring. In most cases, the runner is made of stainless steel. The water flow through the labyrinth seals is a leakage flow and is not utilized by the runner. On high head turbines, the leakage water is normally utilized as cooling water for the generator, transformers, and bearings.

• Draft Tube: - The draft tube forms the water conduit from the runner to the draft outlet. It consists of the draft tube cone and the draft tube steel plate lining. It consists of the draft tube cone and the draft tube steel plate lining. The aim of the draft tube is also to convert the main part of the kinetic energy at the runner outlet to pressure energy at the draft tube outlet. This is achieved by increasing the cross-section area of the draft tube in the flow direction. In an intermediate part of the bend, however, the draft tube cross-sections are decreased instead of increased in the flow direction to prevent separation and loss of efficiency. The draft tube cone is a welded steel plate design and consists normally of two parts, the upper and lower cone. The inlet part of the upper cone is made of stainless steel. It is normally provided with two manholes for inspection of the runner from below. The lower part is designed as a dismantling piece and is mounted to a flange on the draft tube bend top. This design is always used for units where the runner is dismantled downwards. For units being dismantled upwards, the draft tube cone is made in one piece. The draft tube lining is completely embedded in concrete.

Important relation for Francis turbine

The following are the important relations for Francis turbines:

1. The ratio of the width of the wheel to its diameter is given as

n =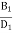

The value of n varies from 0.10 to 0.40.

2.     The flow ratio is given as,

Flow ratio = 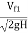and varies from 0.15 to 0.30.

3.     The speed ratio = 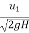and varies from 0.6 to 0.9.

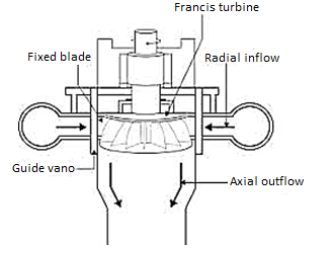
Fig: Francis turbine

Kaplan Turbine

Introduction

A higher specific speed corresponds to a lower head. This requires that the runner should admit a comparatively large quantity of water. For a runner of a given diameter, the maximum flow rate is achieved when the flow is parallel to the axis. Such a machine is known as an axial flow reaction turbine. An Australian engineer, Vikton Kaplan first designed such a machine. The machines in this family are called Kaplan Turbines.

Fig: Kaplan Turbine

Development of Kaplan Runner from the Change in the Shape of Francis Runner with Specific Speed

The Francis runner (radial flow runner) at low, normal, and high specific speeds. As the specific speed increases, the discharge becomes more and more axial. The fourth type is a mixed flow runner (radial flow at inlet axial flow at the outlet) and is known as Dubs runner which is mainly suited for high specific speeds. This type of runner is the most suitable one for very high specific speeds and is known as Kaplan runner or axial flow runner.

From the inlet velocity triangle for each of the five runners, as shown in Figs, it is found that an increase in specific speed (or a decrease in the head) is accompanied by a reduction in inlet velocity V1. But the flow velocity Vf1 at inlet increases allowing a large amount of fluid to enter the turbine. The most important point to be noted in this context is that the flow at the inlet to all the runners, except the Kaplan one, is in radial and tangential directions. Therefore, the inlet velocity triangles of those turbines in a plane containing the radial and tangential directions, and hence the flow velocity Vf1 represents the radial component of velocity.

In the case of a Kaplan runner, the flow at the inlet is in axial and tangential directions. Therefore, the inlet velocity triangle in this case in a place containing the axial and tangential directions, and hence the flow velocity Vf1 represents the axial component of velocity Va. The tangential component of velocity is almost nil at the outlet of all runners. Therefore, the outlet velocity triangle is identical in the shape of all runners. However, the exit velocity V2 is axial in Kaplan and Dubs runner, while it is the radial one in all other runners.

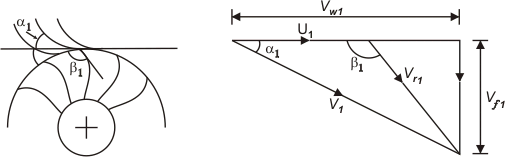
Fig: Francis runner for low specific speeds

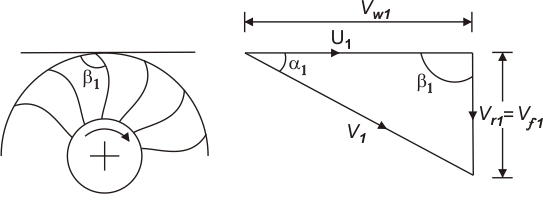
Fig: Francis runner for normal specific speeds

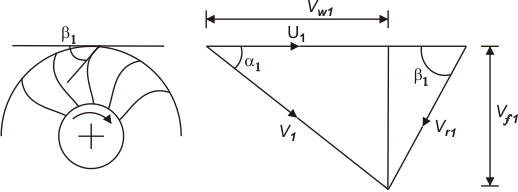
Fig: Francis runner for high specific speeds

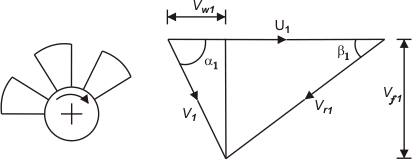
Fig: Kaplan runner

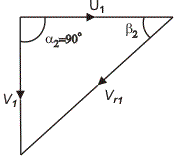
Fig: Outlet velocity triangle

The function of the guide vane is the same as in the case of the Francis turbine. Between the guide vanes and the runner, the fluid in a propeller turbine turns through a right-angle into the axial direction and then passes through the runner. The runner usually has four or six blades and closely resembles a ship's propeller. Neglecting the frictional effects, the flow approaching the runner blades can be considered to be a free vortex with whirl velocity being inversely proportional to the radius, while on the other hand, the blade velocity is directly proportional to the radius. To take care of this different relationship of the fluid velocity and the blade velocity with the changes in radius, the blades are twisted. The angle with the axis is greater at the tip than at the root.

Fig: A propeller of Kaplan turbine

Different types of draft tubes incorporated in reaction turbines The draft tube is an integral part of a reaction turbine. Its principle has been explained earlier. The shape of the draft tube plays an important role especially for high specific speed turbines since the efficient recovery of kinetic energy at runner outlet depends mainly on it. Typical draft tubes, employed in practice, are discussed as follows.

1. Straight divergent tube: - The shape of this tube is that of the frustum of a cone. It is usually employed for low specific speed, vertical shaft Francis turbine. The cone angle is restricted to 8 0 to avoid the losses due to separation. The tube must discharge sufficiently low under tailwater level. The maximum efficiency of this type of draft tube is 90%. This type of draft tube improves the speed regulation of a falling load.

2. Simple elbow type: - The vertical length of the draft tube should be made small to keep down the cost of excavation, particularly in rock. The exit diameter of the draft tube should be as large as possible to recover kinetic energy at the runner's outlet. The cone angle of the tube is again fixed from the consideration of losses due to flow separation. Therefore, the draft tube must be bent to keep its definite length. A simple elbow type draft tube will serve such a purpose. Its efficiency is, however, low (about 60%). This type of draft tube turns the water from the vertical to the horizontal direction with a minimum depth of excavation. Sometimes, the transition from a circular section in the vertical portion to a rectangular section in the horizontal part is incorporated in the design to have a higher efficiency of the draft tube. The horizontal portion of the draft tube is generally inclined upwards to lead the water gradually to the level of the tailrace and to prevent the entry of air from the exit end.

Key Takeaways:

• Flow ratio: - The ratio of the two for a well-designed Francis turbine is probably around 1:1. The Francis design has been used with head heights of from 3 to 600 m but it delivers its best performance between 100 and 300 m.
• Speed ratio: - The Tip Speed Ratio (TSR) is an extremely important factor in wind turbine design. TSR refers to the ratio between the wind speed and the speed of the tips of the wind turbine blades. The further away from the center, the faster the blades spin.
• Vortex: - In fluid dynamics, a vortex (plural vortices/vortexes) is a region in a fluid in which the flow revolves around an axis line, which may be straight or curved.

4.6 Constructional details of Francis and Kaplan turbines

Francis turbines

• Figure shows a Francis turbine which is a mixed flow type reaction turbine.
• The water from penstock enters a scroll casing which completely surrounds the runner.

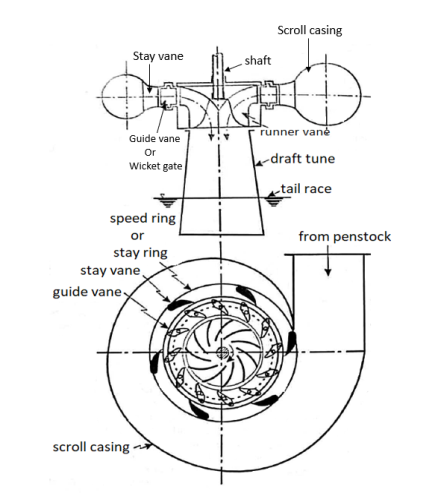
• The purpose of the casing is to provide an even distribution of water around the circumference of the turbine runner, maintaining an approximately constant velocity for the water so distributed.
• The casing is made of a cast steel, plate steel, concrete and steel depending upon the pressure to which it is subjected.
• From the scroll casing the water passes through a speed ring held together by series of fixed vanes called stray vanes.
• The speed wing has two functions to perform.
• It directs the water from the scroll casing to the guide vanes.
• Further it resists the load imposed upon it by internal pressure of water and the weight of the turbine and the electrical generator and transmits the same to the foundation.
• From the speed ring the water passes through a series of guide vanes provided all around the periphery of the turbine runner.
• The function of guide vanes is to regulate the quantity of water supply to the runner and to direct water onto the runner at an angle approximate to the design.
• Guide vanes can turn about their stems. So as to alter the width of the passage between them.
• The runner of Francis turbine consists of series of curved veins evenly arranged around the circumference in the annular space between two plates.
• The vanes are so shaped that water enters the runner at the outer periphery and leaves it axially at the lower periphery.
• The change in the direction of flow of water from radial to axial as it passes through the runner, produces a circumferential force on the runner which makes the runner to rotate and thus contribute to useful output of the runner.
• The torque produced by the runner is transmitted to the generator through the shaft which is usually connected to the generator shaft by a bolted flange connection.
• The water after passing through runner flows to the tail race through to a draft tube.

Kaplan turbines

• It is an axial flow turbine, which is suitable for relative low heads and hence requires a large quantity of water to develop large amount of power.
• As shown in figure the main component of Kaplan turbine are scroll casing, stay ring arrangement of guide vanes and the draft tube.
  • Scroll Casing

It's a spiral-shaped casing with a smaller cross section area. Water from the penstocks enters the scroll casing, then runs axially through the runner into the guide vanes, where it spins 90 degrees. It shields the turbine's runner, runner blades, guiding vanes, and other internal components from external damage.

• Guide Vane Mechanism

It is the only portion of the turbine that controls the opening and closing of the blades in response to the demand for power. When more power is required, it opens wider to allow more water to hit the rotor's blades, and when less power is required, it closes to stop the flow of water. The turbine will not run efficiently if the guide vanes are missing.

• Draft Tube

The pressure at the exit of a Reaction Turbine's runner is usually lower than air pressure. The water near the exit cannot be released directly into the tail race. Water is discharged from the turbine exit to the tail race through a tube or pipe with a gradually increasing area. Draft Tube is the term given to this expanding tube. The tube is attached to the runner's output on one end and submerged below the water level in the tail-race on the other

• Between guide vanes and the runner the water in Kaplan turbine turns through right angle into axial direction and then passes through the runner.
• The runner of a Kaplan turbine has 4 or 6 blades.

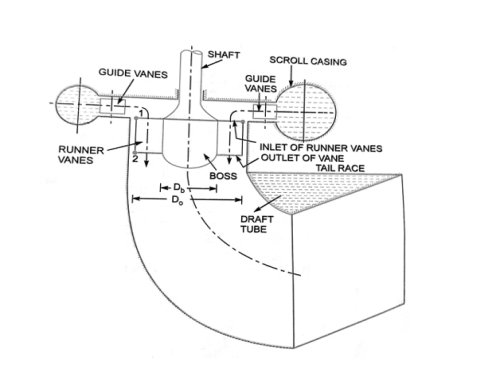
• The blades attached to a hub for boss are so shaped that water flows axially to the runner.
• Ordinarily the runner blades of propeller turbines are fixed, but the Kaplan turbine runner blades can be turned about their own axis, so that their angle of inclination maybe adjust while the turbine is in motion.
• The adjustment of the runner blades is usually carried out automatically by means of servomotor operating inside the hollow coupling of turbine and generator shaft.
• When the vanes are fixed to the hub and are not adjustable, the turbine is known as propeller turbine.

Working

The water coming from the pen-stock is made to enter the scroll casing. The scroll casing is made in the required shape that the flow pressure is not lost. The guide vanes direct the water to the runner blades. The vanes are adjustable and can adjust itself according to the requirement of flow rate. The water takes a 90 degree turn, so the direction of the water is axial to that of runner blades.

As the water strikes, the runner blades begin to revolve due to the water's reaction force. The runner blades twist along their length to maintain an optimal angle of attack for all cross sections of the blades, resulting in increased efficiency. The water enters the draft tube from the runner blades, where its pressure energy and kinetic energy are reduced. The conversion of kinetic energy to pressure energy leads in a rise in water pressure. The turbine's spin is utilised to turn the generator's shaft, which produces electricity.

4.7 Velocity triangles

• Velocity triangles for reaction turbines are as shown in figure.

• From the velocity triangles, the work done by the water on the runners, horsepower and efficiency of the turbine can be obtained.

The work done per second on the runner by water is given by equation

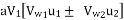
= Q[

Where

Velocity of whirl at inlet and outlet

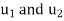= Tangential velocity of wheel of inlet and outlet

The work done per second per unit weight of water per second

=

=

=

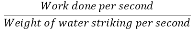
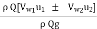
Hydraulic efficiency =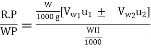

=

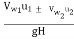
Where

RP = Runner power

WP = Water power

If discharge is radial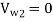

= =

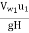
4.8 Power and efficiency of Francis and Kaplan turbines

Francis turbine

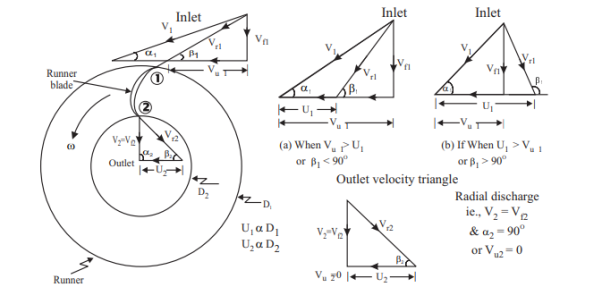
The velocity triangle at the Francis turbine's inlet and output is shown similarly to that of an inward flow reaction turbine. Because the discharge of the Francis turbine is radial at the outlet, the velocity of the whirl at the outlet (Vw2) will be zero. As a result, the amount of work done each second by water on the runner will be

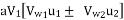
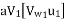
And work done per second per unit weight of water striking/s =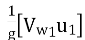

Hydraulic efficiency will be given by,

KAPLAN Turbine

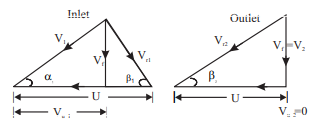
Discharge

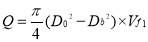
D0 is outer diameter of runner

Db is Diameter of hub

Vf1 inlet flow velocity

Db/ D0 = 0.35 to 0.60

Flow ratio

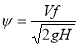
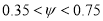
Velocity of flow at inlet and outlet are equal

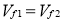
Peripheral velocities are equal

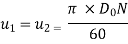
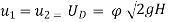
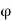  is Speed Ratio

Area of Flow at inlet = Area at outlet

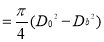
From inlet velocity triangle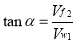

Hydraulic efficiency

=

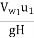
Q. A Kaplan turbine produces 80,000 HP (58,800 kW) under a head of 25m which has an overall efficiency of 90%. Taking the value of speed ratio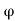  = 1.6, flow ratio 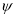= 0.5 and the hub diameter = 0.35 times the outer diameter. Find the diameter and the speed of the turbine.

Solution

P = 80,000 HP = 58,800 kW,

H = 25m,

n0= 0.9,

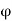  = 1.6,

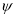= 0.5,

Db/ D0 = 0.35,

Q=266.4 m3/s

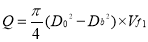
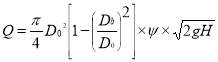
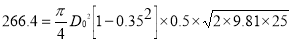
D0 =5.91m

UD = 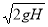=1.6 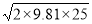=35.4355 m/s

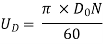
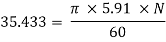
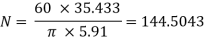
N =144.5043 rpm

4.9 Principles of similarity

The notion of similarity underpins dimensional analysis as a whole. For perfect likeness between a model and a prototype, three conditions must be met.

Geometric similarity: The model must have the same shape as the original, although it can be scaled up or down by a constant factor.

Kinematic similarity: The velocity at any point in the model flow must be proportional to the velocity at the homologous point in the prototype flow by a constant scaling factor. (In other words, the flow streamlines must be identical in shape.)

Dynamic similarity: All forces in the model flow must scale to the equivalent forces in the prototype flow by a constant factor. In other words, for the model and prototype, the relative importance of different types of forces (e.g., viscous and inertial forces) must be the same.

This necessitates that the model and prototype have the same dimensionless parameters (e.g., the same Reynolds number), despite the fact that the dimensional variables may (and generally do) differ. For every p pi groups that can be specified mathematically for two different flow circumstances, dynamic similarity requires that

k, model   k, prototype, k=1…….. p

As a result, while geometric and kinematic similarities are required, they are not sufficient for dynamic similarity. That is, geometric and kinematic similarities are attainable, but dynamic similarity is not.

It is possible to anticipate the performance of one machine from the results of tests on a geometrically similar machine using this technique, as well as the performance of the same machine under settings other than the test conditions. Geometrical similarity must be applied to all significant sections of a fluid machine, such as the rotor, the entrance and discharge tubes, and so on. A homologous series is made up of machines that are geometrically comparable. As a result, members of a series with a similar shape are essentially enlargements or reductions of one another. The velocity vector diagrams at the intake and outlet of the rotor of one machine must be similar to those of the other if the two machines are kinematically identical. As a result, geometrical similarity of the intake and outlet velocity diagrams is a need for dynamic similarity.

Flow with a free surface does not occur in practically all fluid devices, and the gravitational force has a small influence.

As a result, rather than using H alone as the variable, it is more rational to consider the energy per unit mass gH as the variable, such that acceleration due to gravity does not appear as a separate variable. As a result, there are now eight distinct variables D, Q, N, gH, ρ, µ, E and P. The number of independent terms (dimensionless terms) required are five as the number of fundamental dimensions necessary to represent these variables is three. Fundamental Quantities for Turbo-machines are N rotational speed , impeller diameter D  and fluid density  . The expressions for the terms are found using Buckingham's theorem with D, N, and as the recurring variables.

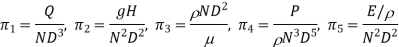
All of the machine's lengths are proportional to D, and all of its areas are proportional to D2. As a result, at any point in the machine, the average flow velocity is proportional to Q/D2 The rotor's peripheral velocity is proportional to the product N.D The first term can be written as follows:

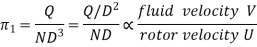
Key Takeaway

Geometric and kinematic similarities are attainable, but dynamic similarity is not.

These similarities are used to anticipate performance similar machines.

4.10 Unit and specific speed

Unit Quantities

The results are described in terms of numbers that can be acquired when the head on the tune is lowered to unity in order to forecast the behaviour of a turbine functioning under varied conditions of head, speed, output, and gate opening. The conditions of the turbine under unit head are such that the turbine's efficiency is not impaired. The following are the three important unit quantities which must be studied under unit head:

Unit Speed

The speed of a turbine operating under a unit head is defined as this (i.e., a head of 1 m). It is indicated by the letter N. The following is the expression for unit speed (N):

Let

N = Speed of a turbine under a head H,

H = Head under which a turbine is working.

u= Tangential velocity.

The tangential velocity, absolute velocity of water and head on the turbine are related as

u α V. And V α √H

Therefore,

u α √H

Also tangential velocity (u) is given by

u= πDN/60

For a given turbine, the diameter (D) is constant.

Therefore, u α N and  N α √H

N=K₁ √H

Where K, is a constant of proportionality. If head on the turbine becomes unity, the speed becomes unit speed or

When H = 1, N= N₂

Substituting these values in equation (if), we get

N₁ = K₁ √1 = K₁

Substituting the value of K, in equation,

N = Nu √H   Or   Nu = N /√H

Unit Discharge

It is the discharge that passes through a turbine that is operating under a unit head (i.e., 1m). The letter 'Q' stands for it. The unit discharge expression is as follows:

Let

H is the turbine's water head

Q = the discharge that passes through it, when the turbine's head is H,

a=area of water flow.

The discharge passing through a given turbine under a head 'H' is given by.

Q = Area of flow x Velocity

But for a turbine, area of flow is constant and velocity is proportional to √H.

Q α Velocity α √H    or

Q= K₂ √H

Where K₂ is constant of proportionality.

If H = 1, Q = Qu………………(By definition)

Substituting these values in equation we get

Qu = K₂ √1 = K₂.

Substituting the value of K₂ in equation, we get

Q=Qu √H   or   Qu= Q/ √H

Unit Power

It is defined as the power developed by a turbine, working under a unit head (i.e., under a head or 1 m ). It is denoted by the symbol 'P. The expression for unit power is obtained as:

Let

H = Head of water on the turbine,

P = Power developed by the turbine under a head of H. Q = Discharge through turbine under a head H.

The overall efficiency (n) is given as

no= Power developed / Water power

 =

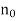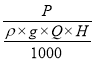
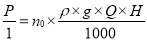
P α Q x H

But Q α √H

Therefore

P α H√H

P = K3 H ³/2

Where K3, is a constant of proportionality.

When H=1m then P=Pu

Pu = K+ (1) ³/2 = K3.

Substituting the value of K, in equation (iv), we get

P= Pu H³/2   or   Pu= P/ H³/2

Q. A turbine develops 9000 kW when running at 10 rpm. The head on the turbine is 30 m. If the head on the turbine is reduced to 18 m, determine the speed and power developed by the turbine.

Solution

Given:

Power developed, P₁ = 9000 kW

Speed, N₁ = 100 rpm.

Head, H₁ = 30 m

Loss of head to, H₂ = 18 m

Speed = N₂

Power= P₂

By unit Quantities

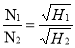
Therefore,

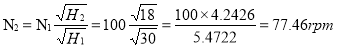
Also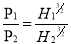

Therefore

Specific Speed

It is described as the speed of a turbine that is similar to the actual turbine in shape, geometrical dimensions, blade angles, gate opening, and so on, but is of a size that produces unit power when working under unit head. The sign Ns is used to represent it. Because each type of turbine has a different particular speed, the specific speed is used to compare the different types of turbines.

In M.K.S. Units, unit power is taken as one horse power and unit head as one metre. But in S.I. Units, unit power is taken as one kilowatt and unit head as one metre.

Derivation of the Specific Speed.

The overall efficiency (n) of any turbine is given by,

no= Shaft power/ Water power

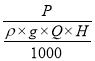= ---------------------------------------------------------------1

Where H= Head under which the turbine is working,

Q = Discharge through turbine,

P= Power developed or shaft power.

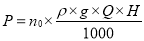
P α Q x H (as no and are constant) ----------------------------------------2

Now let

D = Diameter of actual turbine,

N = Speed of actual turbine,

u = Tangential velocity of the turbine,

Ns= Specific speed of the turbine,

V = Absolute velocity of water.

The absolute velocity, tangential velocity and head on the turbine are related as,

u α V. And V α √H

Therefore,

u α √H                      -------------------------------------------3

Also, tangential velocity (u) is given by

u= πDN/60

u α DN                -------------------------------------------4

From 3 and 4

√H α DN         -------------------------------------------5

Discharge through turbine        

Q = Area of flow x Velocity

Area α width x D, but width α D

Therefore, Area α D2

Also, Velocity α √H  

Q α D2 α √H  

From equation 5

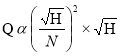
Substituting Q in equation 2

P α Q x H

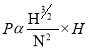
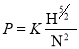                                 ----------------------------------------------------6

Where K is constant of proportionality

If P=1, H=1 N=Ns (specific Speed)

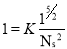
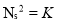
Put in equation 6

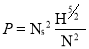
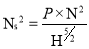
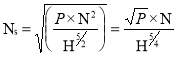
Q. A turbine is to operate under a head of 25 m at 100 rpm. The discharge is 9 cumec. If the efficiency is 90%, determine:

(i)                Specific speed of the machine, (ii) Power generated,

Solution. Given:

Head, H = 25 m

Speed, N = 100 rpm.

Discharge. Q = 9 cumec = 9 m³/s

Efficiency, no = 90% = 0.90

Now using relation.

(i)                P= Power developed or shaft power.

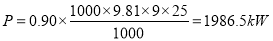
(ii)              Specific Speed of Turbine

4.11 Performance characteristics

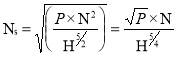
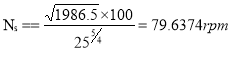
• Important parameters which are varied during a test on a turbine

1)     Speed (N)

2)     Head (H)

3)     Discharge (Q)

4)     Power (P)

5)     Overall efficiency (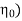

6)     Gate opening

• Out of the above 6 parameters, three parameters namely speed head and discharge are independent parameters.
• Out of the three independent parameters (N, H, Q) one of the parameters is kept constant and the variation of the other four parameters with respect to anyone of the remaining two independent variables are plotted and various are obtained.
• These are called characteristic curves.
• The following are the important characteristic curves of a turbine.

Constant head curves

• These curves are obtained by keeping head constant and a constant gate opening on the turbine.
• The speed of the turbine is varied by changing load on the turbine.
• For each value of speed, the corresponding values of the power(P), discharge(Q) are obtained.

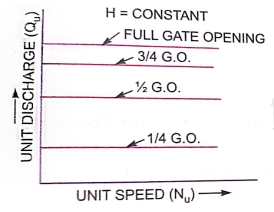
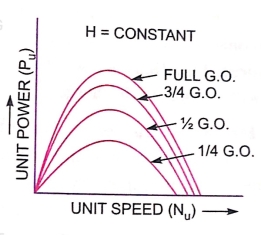
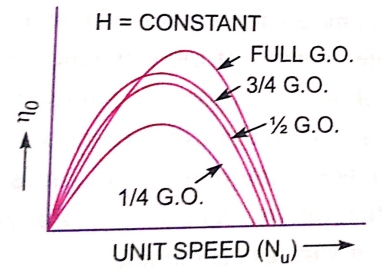
For a Pelton wheel

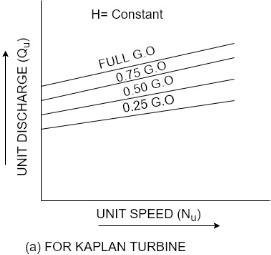
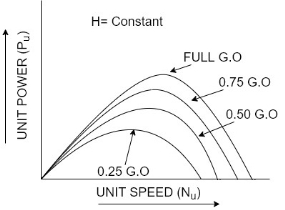
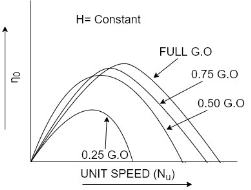
For reaction turbines

• Then the overall. 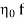or each value of the speed is calculated.
• From these reading the values of unit speed ,unit power 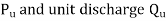a determined.
• Taking 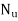as abscissa, the values of 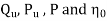are plotted as shown in figure by changing the gate opening, the values of  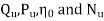 are determined and taking as abscissa.
• Figure a show the main characteristic curves for Pelton wheel and figure b shows the main characteristic curves for reaction turbines.

Operating characteristic curves for constant speed curves

• Operating characteristic curves are plotted when speed on the turbine is constant.
• In case of turbines, the head is generally constant.

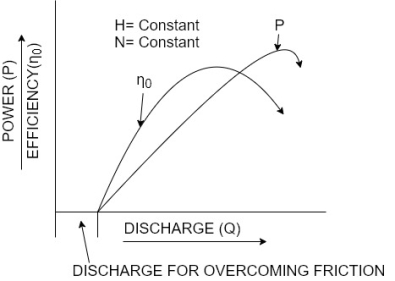
• For operating characteristics N and H are constant and hence the variation of power and efficiency with respect to discharge Q are plotted.
• The power curve for turbines shall not pass through the origin because certain amount of discharge is needed to produce power to overcome initial friction.
• Hence the power and efficiency curves will be slightly away from the origin on the x-axis, as to overcome initial friction certain amount of discharge will be required.
• Shows the variation of power and efficiency with respect to discharge.

Constant efficiency curves or Muschel curves or iso-efficiency curves

• These curves are obtained from speed versus efficiency and speed versus discharge curves for different gate opening.
• For a given efficiency from the    curves, there are two speeds.
• From 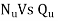curves, corresponding to two values of speeds there are two values of discharge.

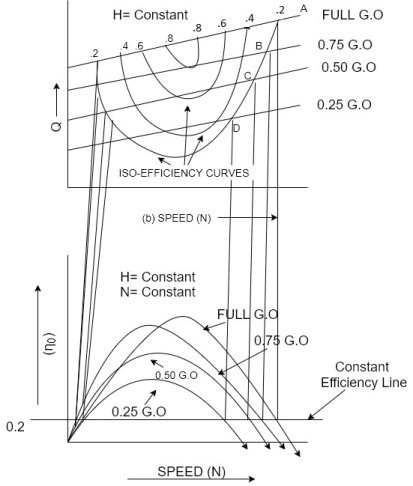
• Hence for a given efficiency there are two values of discharge for the particular gate opening.
• This means for a given efficiency there are two values of speeds and two values of discharge for a given gate opening.
• If the efficiency is maximum there is only one value.
• These two values of speed and two values of discharge corresponding to particular gate opening are plotted as shown in figure.
• The procedure is repeated for different gate opening and the curves Q vs N are plotted.
• The points having the same efficiency are called iso- efficiency curves.
• These curves are helpful for determining the zone of constant efficiency and for predicting the performance of the turbine at various efficiencies.
• For plotting the iso-efficiency curves horizontal lines representing the same efficiency are drawn on the       speed curves.
• The points at which these lines cut the efficiency curves at various gate openings are transferred to the corresponding Q~ speed curves.
• The points having the same efficiency are less then joined by a smooth curve.
• These smooth curves represent the ISO efficiency curve.

4.12     Selection of water turbines

Some of the Factors affecting the Selection of Hydraulic Turbines

1. Head
2. Specific speed
3. Rotational speed
4. Efficiency of the turbine

Based on Head

Based on head requirement following Turbines are selected

Based on Specific Speed

Specific speed plays an important role for selecting the type of the turbine. Also the performance of a turbine can be predicted by knowing the specific speed of the turbine. The type of turbine for different specific speed is given in Table below

Cavitation is most commonly seen in reaction turbines. So, while choosing a turbine, the cavitation factor for that particular turbine should be assessed to see if it is in a safe zone or not. The cavitation factor is determined by the turbine's specific speed. It is critical, particularly in the case of Kaplan, propeller, and bulb turbines.

Based on Rotational speed

The turbine's rotational speed is determined by the turbine's specific speed, frequency, and number of pairs of poles in the electric generator. As a result, the specified turbine's specific speed should provide the equivalent amount of generator rotation speed.

Based on Efficiency of turbine

Efficiency of turbines = Francis Turbine > Kaplan Turbine > Pelton Turbine

In general, the turbine's efficiency is highest when it is operating at a specified load. When a part-load or overload problem occurs, efficiency suffers, which is costly.  Kaplan turbines are preferred in this circumstance. 

References:

1. Introduction to fluid mechanics and Fluid machines by S.K Som, Gautam Biswas, S Chakraborty.

2. Fluid mechanics and machines by R.K Bansal.

3. F. M. White, Fluid Mechanics, 6th Ed., Tata McGraw-Hill, 2008.

4. Fluid Mechanics and Its Applications by V.K. Gupta et.al.

5. Fluid Mechanics by Yunus Cengel.