Unit – 2
Second law of thermodynamics and Entropy
A thermal energy reservoir (TER) is defined as a large body with infinite heat capacity that can absorb or reject an infinite amount of heat without causing significant changes in its thermodynamic coordinates. The changes that occur in the large body as heat enters or exits it are so slow and minute that all processes within it are quasi-static.
The source is the thermal energy reservoir TER from which heat Q1 is transferred to the system operating in a heat engine cycle. The sink is the thermal energy reservoir TER, to which heat Q2 is rejected from the system during a cycle.
A typical source is a constant-temperature furnace that continuously burns fuel, and a typical sink is a river, sea, or the atmosphere itself.
A mechanical energy reservoir (MER) is a large body surrounded by an adiabatic impermeable wall that can store work as potential energy (a raised weight or wound spring) or kinetic energy (such as a rotating flywheel). Within a MER, all processes of interest are essentially quasi-static. An MER receives and delivers mechanical energy in a quasi-statistic manner.
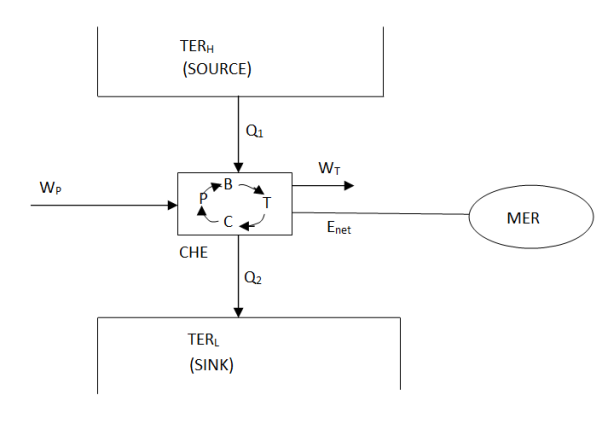
Fig 1
Above figure show a cyclic heat engine exchanging heat with a source and a sink and delivering W(net) in a cycle to an MER
Whether it is coal, oil, gas, or nuclear power, 80 percent of the world's electricity is derived from heat sources, and almost all of the energy conversion processes used to convert thermal energy to electrical energy include an intermediate step of converting heat energy to mechanical energy in some form of heat engine. To meet this demand, a wide range of energy conversion systems that optimise the conversion process to the available heat source have been developed.
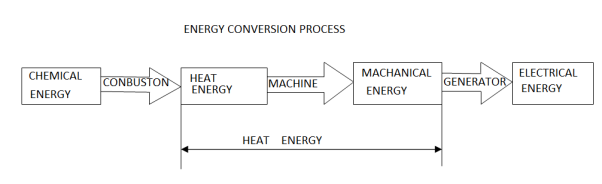
Fig 2
Despite over 250 years of development since James Watt's steam engine was first fired up, the best conversion efficiency achieved today for combined cycle steam and gas turbine systems is only around 60%. Steam turbines typically have efficiency rates of 35 percent to 45 percent, piston engines have rates of 20 percent to 30 percent, and OTEC ocean thermal power plants have rates as low as 3 percent.
Carnot investigated the efficiency of heat engines in 1824, which was expanded upon by Chaperon, who provided analytical tools in 1834, Kelvin, who stated the Second Law of Thermodynamics in 1851, and Clausius, who introduced the concept of entropy in 1865.
At any given point in time, every thermodynamic system exists in a specific state defined by the properties of its constituents such as heat, temperature, pressure, volume, density, entropy, and phase (liquid, gas, etc.). Thermodynamics is concerned with the conversions of heat and other forms of energy in the system, as well as the associated energy flows.
A thermodynamic cycle involves the application of energy in one form to change the state of the system, followed by the extraction of energy in a different form to return the system to its original state. In a heat engine, energy is applied as heat to change the state of a working fluid and then extracted as mechanical work to return the working fluid to its initial state. A heat engine, in other words, is a system in which energy is exchanged between an energy conversion system and its surroundings.
Although the working fluid in a heat engine may operate in a closed cycle, the "system" and "state of the system" are defined to include both the physical "engine" and the working environment or surroundings.
Key takeaways
Every thermodynamic system exists in a particular state which is defined by the properties of its components such as heat, temperature, pressure, volume, density, entropy, and phase (liquid, gas etc.) at a given point in time. Thermodynamics concerns the conversions between heat and other forms of energy in the system and the related energy flows
In a thermodynamic cycle net heat transfer takes place to the system and a net work transfer from the system. A heat engine executes Heat Engine cycle. Its Working Fluid may be in the form of Gas or Liquid.
It receives heat from heat source and produces the mechanical work and remainder of energy is rejected to heat sink.
“The heat engine is a device that transfers energy from an object at a higher temperature to an object at a lower temperature when work is done on the system.”
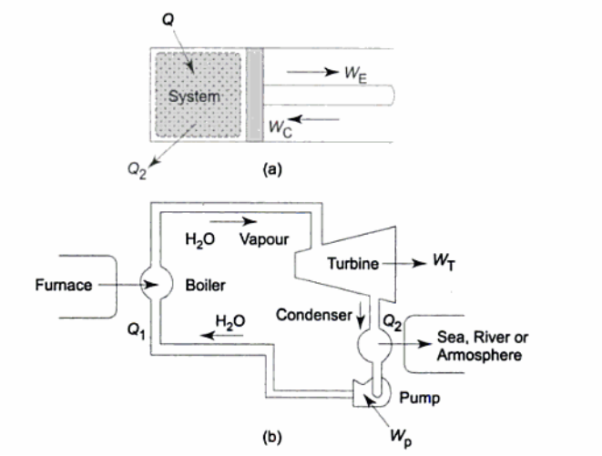
Fig 3
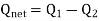
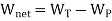
As,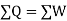 
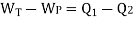
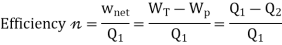
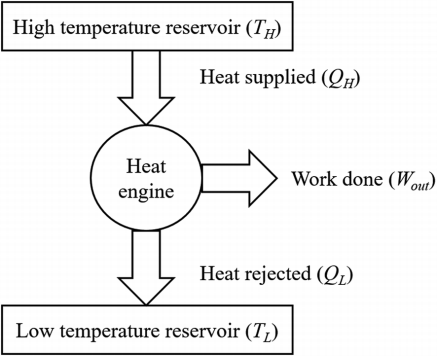
Fig 4
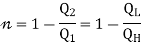
Or
Example of Heat Engine:
- Gasoline and diesel engines
- Jet engines
- Steam turbines
The reverse heat engine is a device that transfers energy from an object at a lower temperature to an object at a higher temperature by doing work on the system.
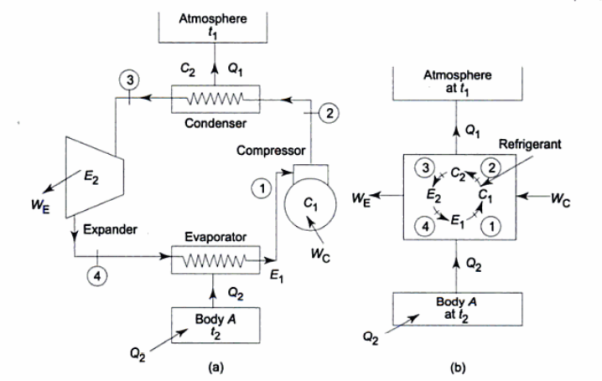
Fig 5
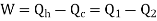
There are two Types of Reversed Heat Engine explained below.
It utilizes heat transfer from Low to High Temperature. i.e., Qc = Q2 and delivers Qh = Q1. This requires work input, as Temp is flowing from Cold to Hot. Which produces Heat Transfer. Qc comes from outside air (Temp below freezing to Indoor Space)
Compressor raises the temperature & pressure of gas and forces it into condenser coils, that are inside the heated space. The Gas is converted into Liquid. Liquid flows back through expansion valve (Pressure Reducing). Liquid when cooled through expansion returns to outer evaporator.
Compressor squeeze gas particles, leading to generation of high pressure. So, temperature also increases. These gas particles pass through tubes which comes in contact with outer air. The gas cools & condensates, which goes into evaporator through expansion valve. Gas spreads out and pressure drops, leading to increase in temperature. A fan blows over this.
Here, Efficiency is Measured through Coefficient of Performance.
Quality of Heat pump is judged by how much energy is transferred by heat into warm space (Qh). Compared with how much input work (W) is required.
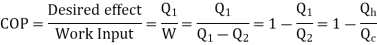
The functioning Is same as Heat Pump, But the difference is
Air Conditioner = “Heat is transferred outdoors from inside a room “.
Refrigerator = ‘Heat is moved out of the inside into surrounding”
Quality of Refrigerator/AC is judged by how much energy is removed by heat Qc from cold, compared with how much work (W) is required.
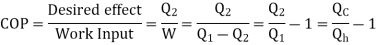
Key Takeaways:
- For hear engine
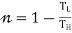
- For heat Pump
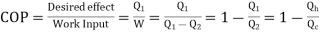
- For Refrigerator
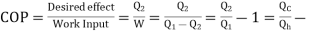
Second Law of Thermodynamics:
STATEMENTS OF SECOND LAW OF THERMODYNAMICS:
The second law of thermodynamics has two statements put forward by two scientists.
- Clausius statement: “It is impossible for a self-acting machine working in a cyclic process unaided by any external agency, to convey heat from a body at a lower temperature to a body at a higher temperature”. In other words, heat cannot flow from a colder to a hotter body.
- Kelvin Planck statement: “It is impossible to construct an engine, which while operating in a cycle produces no other effect except to extract heat from a single reservoir and do equivalent amount of work”.
i.e., “A heat engine can never be 100% efficient,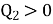 
. Which means always there a heat rejection.
If 
means 
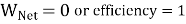. i.e., Only 1 Reservoir is working. Which violates Kelvin-Plank Statement. This is Known as PMM 2.
Although the Clausius and Kelvin-Planck statements appear to be different, they are equivalent in the sense that a violation of either statement implies violation of other.
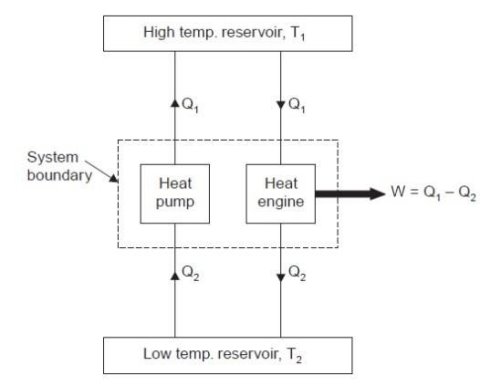
Fig 6
Consider a higher temperature reservoir T1 and low temperature reservoir T2. Fig. Shows a heat pump which requires no work and transfers an amount of Q2 from a low temperature to a higher temperature reservoir (which is a violation of the Clausius statement).
Let an amount of heat Q1 (greater than Q2) be transferred from high temperature reservoir to heat engine which develops a net work, W = Q1 – Q2 and rejects Q2 to the low temperature reservoir. Since there is no heat interaction with the low temperature, it can be eliminated. The combined system of the heat engine and heat pump acts then like a heat engine exchanging heat with a single reservoir, which is the violation of the Kelvin-Planck statement.
The reversible process is an ideal process that never occurs, whereas the irreversible process is a natural process that occurs frequently in nature. When we tear a page from a book, we can't go back and 'un-tear' it. This is an irreversible process. Water can be condensed in the form of rain when it evaporates. This is a process that can be reversed.
Reversible Process
A thermodynamic process is reversible if it can be reversed in such a way that both the system and its surroundings return to their original states, with no other changes occurring anywhere else in the universe. It means that at the end of the reverse process, both the system and its surroundings are returned to their initial states.
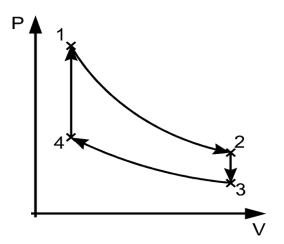
Fig 7
In the figure above, the system has undergone a change from state 1 to state 2. The reversible process can reverse completely and there is no trace left to show that the system had undergone thermodynamic change. During the reversible process, all the changes in state that occur in the system are in thermodynamic equilibrium with each other.
Internally reversible process
If no irreversibility’s occur within the system's boundaries, the process is internally reversible. A system goes through a series of equilibrium states in these processes, and when the process reverses, the system goes through exactly the same equilibrium states while returning to its initial state.
Externally reversible process
No irreversibility’s occur outside the system boundaries during an externally reversible process. Heat transfer between a reservoir and a system is an externally reversible process if the system and reservoir have the same temperature at the point of contact.
A process can be reversible only when its satisfying two conditions
- Dissipative force must be absent.
- The process should occur in infinite small time.
Fig 8
In layman's terms, a reversible process is one that can be completely reversed. This means that the system's final properties can be perfectly reversed back to the original properties. Only if the changes in the process are infinitesimally small can the process be perfectly reversible. Because it is impossible to trace these extremely small changes in such a short period of time in practise, the reversible process is also an ideal process. The changes that take place during the reversible process are in balance with one another.
Irreversible Process
Irreversible processes occur as a result of deviating from the curve, which reduces the amount of overall work done. An irreversible process is one that deviates from equilibrium in thermodynamic terms. In terms of pressure and volume, it occurs when the pressure (or volume) of a system change so dramatically and instantly that the volume (or pressure) does not have time to stabilise.
Fig 9
Allowing a certain volume of gas to escape into a vacuum is a classic example of an irreversible process. The system and surroundings are not in equilibrium during the expansion process because pressure is released on a sample, and it is allowed to occupy a large space. Little work is done here. However, significant work is required, along with a corresponding amount of energy dissipation as heat flows to the environment. This is done to reverse the process.
THE CARNOT VAPOR CYCLE
The Carnot cycle is the most efficient cycle when operating between two temperatures. As a result, it is natural to consider the Carnot cycle first as a potential ideal cycle for vapour power plants.
The Carnot cycle, on the other hand, is not a good model for power cycles.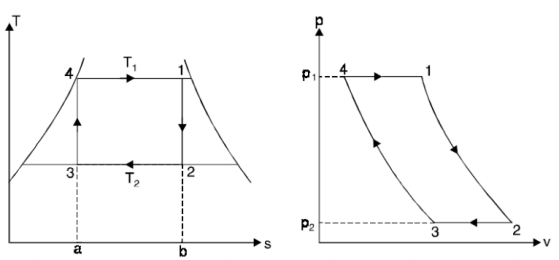
Fig 10
- Process 4-1: 1 kg of boiling water at temperature T1 is heated to form wet steam of dryness fraction x1. Thus, heat is absorbed at constant temperature T1 and pressure p1 during this operation.
- Process 1-2: steam is expanded isentropically to temperature T2 and pressure p2. The point ‘2’ represents the condition of steam after expansion.
- Process 2-3: heat is rejected at constant pressure p2 and temperature T2. As the steam is exhausted it becomes wetter and cooled from 2 to 3.
- Process 3-4: the wet steam at ‘3’ is compressed isentropically till the steam regains its original state of temperature T1 and pressure p1.
Thus, cycle is completed.
Net work done = Heat supplied – heat rejected
= T1 (s2 - s3) - T2 (s2 - s3) = (T1 – T2) (s2 - s3)
Carnot Efficiency η = Work done / Heat supplied = (T1 – T2) (s2 - s3) / T1 (s2 - s3) = (T1 – T2) / T1
Limitations or Impracticalities of Carnot Cycle:
Though Carnot cycle is simple (thermodynamically) and has the highest thermal efficiency for given values of T1 and T2, yet it is extremely difficult to operate in practice because of the following reasons:
- It is difficult to compress a wet vapour isentropically to the saturated state as required by the process 3-4.
- It is difficult to control the quality of the condensate coming out of the condenser so that the state ‘3’ is exactly obtained.
- The efficiency of the Carnot cycle is greatly affected by the temperature T1 at which heat is transferred to the working fluid. Since the critical temperature for steam is only 374°C, therefore, if the cycle is to be operated in the wet region, the maximum possible temperature is severely limited.
- The cycle is still more difficult to operate in practice with superheated steam due to the necessity of supplying the superheat at constant temperature instead of constant pressure.
Some of these problems could be eliminated by executing the Carnot cycle in a different way, as shown in Fig. B.
Fig 11
This cycle, on the other hand, has additional issues, such as isentropic compression to extremely high pressures and isothermal heat transfer at variable pressures.
As a result, we conclude that the Carnot cycle is not a realistic model for vapour power cycles and cannot be approximated in actual devices.
Carnot engine
A Carnot engine, also known as a Carnot heat engine, is an idealised engine whose operation is completely reversible. To complete one cycle, this engine employs an ideal gas as the working substance and employs a 4-stroke process.
It takes heat Q1 from source and rejects heat Q2 to sink and performing an amount of work W=Q1−Q2
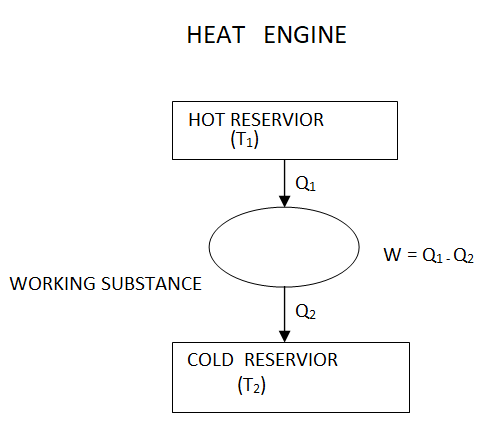
Fig 12
The Carnot's engine is a reversible engine working between two temperature limits.
The complete cycle functions are given below
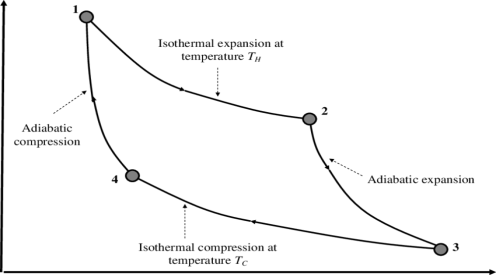
Fig 13 P-V Diagram
1) Reversible Isothermal expansion heat addition at the constant temperature T1 or TH
2) Reversible Adiabatic expansion of ideal gas. In this process, the temperature of the ideal gas falls from source temperature T1 to sink temperature T2.
3) Reversible Isothermal compression of ideal gas at sink temperature T2 or TC. In doing so, it rejects heat Q2 to the sink.
4) Reversible Adiabatic compression of ideal gas where the temperature naturally raises from T2 to T1 and thus the working substance returns to its original state completing the cycle.
The efficiency is given as
η= Work done / Heat input
Thus, W=Q1−Q2 and heat input is obviously Q1
This gives, η= W/Q1
=1−Q2/Q1
It may be shown thermodynamically that Q2/Q1 = T2/T1.
Key takeaways
1) The Carnot's engine is a reversible engine working between two temperature limits.
2) The efficiency is given as
η= Work done / Heat input
Thus, W=Q1−Q2 and heat input is obviously Q1
This gives, η= W/Q1
=1−Q2/Q1
It is impossible for any heat engine to be more efficient than a Carnot engine when operating between two given temperatures:
ηmax = ηcarnot
Consider a heat engine drawing heat Q1 from a heat reservoir at temperature T1, delivering work W and dumping heat Q2 into a heat sink at temperature T2.
The heat engine operates in cycles, that is, it takes in heat Q1, does work W, dumps heat Q2, and in the end returns back to its original unchanged state.
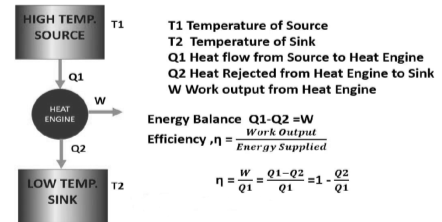
Fig 14
Consider the net change in entropy ΔS of the universe:
The heat reservoir releases a heat Q1 at a constant temperature T1. Thus, the change in its entropy is
∆S1 = -Q1/T1
The heat sink accepts heat Q2 at a constant temperature T2. Thus, the change in its entropy is
∆S2 = Q2/T2
Thus, the net change in entropy of the universe is
∆S=∆S1+ ∆S2
= Q2/T2 – Q1/T1
Using the second law of thermodynamics, ΔS≥0, which implies
Q2/T2-Q1/T1≥ 0
Q2/T2 ≥ Q1/T1
Q2/Q1 ≥ T2/T1
1-Q2/Q1≤ 1-T2/T1
Since the left-hand side represents the efficiency of the given heat engine (η) and the right-hand side is the efficiency of a Carnot engine,
η ≤ ηcarnot=ηmax=ηcarnot
Carnot Theorem corollaries:
It states that “The efficiency of all reversible heat engines operating between the same temperature levels is the same”.
ηA=ηB
Meaning: “Efficiency of all reversible heat engines operating between the same heat reservoirs are the same, the efficiency of reversible engine is independent of the nature of amount of working substance undergoing the cycle.
The working medium has not been mentioned in the Carnot cycle considerations in this section. As a result, they are not limited to an ideal gas and can hold for Carnot cycles in any medium. We previously calculated the Carnot efficiency using an ideal gas as a medium, and the temperature definition used in the ideal gas equation was not critical to the thermodynamic arguments. We can define a thermodynamic temperature scale that is independent of the working medium in more detail. Consider the situation depicted in the diagram below. Figure 6.2, which includes three reversible cycles T1 has a high temperature heat reservoir and T3 has a low temperature heat reservoir. The ratio of the magnitudes of the heat absorbed and rejected in a Carnot cycle has the same value for all systems for any two temperatures T1, T2.
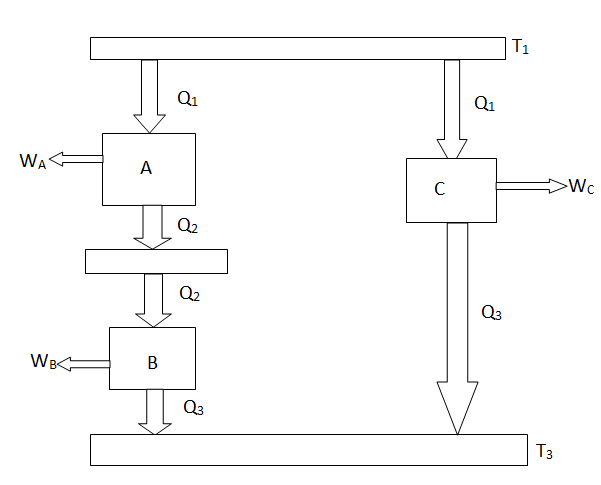
Fig 15: Arrangement of heat engines to demonstrate the thermodynamic temperature scale
We choose the cycles so Q1is the same for A and C. Also, Q3 is the same for B and C. For a Carnot cycle
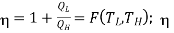is only a function of temperature.
Also
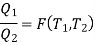
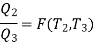
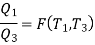
But
Hence
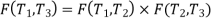
We thus conclude that F (T1,T2) has the form f(T1)/f(T2) and
Similarly F (T2,T3)= f(T2)/f(T3). The ratio of the heat exchanged is therefore
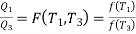
In general,
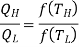
As a result, the ratio of heat exchanged varies with temperature. We could choose any monotonic function, and one option is the simplest: T = f (T) This is the thermodynamic temperature scale, QH/QL = TH/TL. The temperature defined in this way is the same as the temperature of an ideal gas; the thermodynamic temperature scale and the ideal gas scale are equivalent.
This machine violates the second law of thermodynamics because it continuously absorbs heat energy from a thermal reservoir and completely converts the absorbed heat energy into an equivalent amount of work.
This machine will be completely efficient, or we can say that perpetual motion machines of the second kind will be more efficient than the ideal Carnot cycle, which is not possible.
As a result, we can conclude that perpetual motion machines of the second kind do not exist because they violate the second law of thermodynamics.
A graphical representation of PMM2 is shown in the figure below.
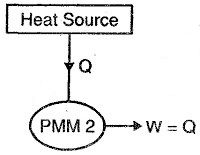
Fig 16
CLAUSIUS INEQUALITY:
The integral of dQ / T is always less than or equal to zero.
∮ dQ / T ≤ 0
This inequality holds true for all cycles in the universe, with no exceptions.
Consider a system connected to a thermal energy reservoir at a constant thermodynamic (i.e., absolute) temperature of TR via a reversible cyclic device to demonstrate the validity of the Clausius inequality.
The cyclic device receives heat ∂QR from the reservoir and supplies heat Q to the system, the temperature at the boundary being T (a variable), while producing work ∂Wrev.
The system produces work ∂Wsys as a result of this heat transfer.
Balancing the combined system identified by dashed lines yield
ΔWc = δQR - dEc
Considering that the cyclic device is a reversible one, we have
δQR / TR = δQ / T
Eliminating ∂QR from the two relations above yields
ΔWc = TR δQ / T - dEc
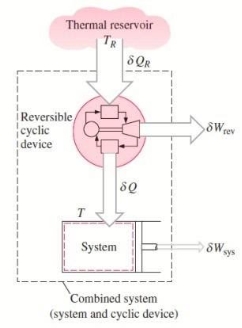
Fig 17
We let the system go through one cycle while the cyclic device goes through an integral number of cycles. The preceding relationship then becomes
Wc = TR ∮ dQ / T
The net work for the combined cycle is represented by ∂WC, which is the cyclic integral of WC.
During a cycle, it appears that the combined system exchanges heat with a single thermal energy reservoir while involving (producing or consuming) work Wc. We reason that Wc cannot be a work output and thus cannot be a positive quantity based on the Kelvin-Planck statement of the second law, which states that no system can produce a net amount of work while operating in a cycle and exchanging heat with a single thermal energy reservoir.
∮ dQ / T ≤ 0
Entropy is defined as a measure of randomness or disorder of a system.
Aside from the general definition, there are several definitions for this concept.
We do not consider the microscopic details of a system from the standpoint of entropy in thermodynamics. Entropy, on the other hand, is used to describe a system's behaviour in terms of thermodynamic properties such as temperature, pressure, entropy, and heat capacity.
This thermodynamic description took into account the systems' state of equilibrium. Meanwhile, the statistical definition developed later focused on the thermodynamic properties defined in terms of the statistics of a system's molecular motions. The entropy of a molecular system is a measure of its disorder.
By the Clausius definition, if an amount of heat Q flows into a large heat reservoir at temperature T above absolute zero, then the entropy increase is ΔS = Q/T. This equation effectively gives an alternate definition of temperature that agrees with the usual definition. Assume that there are two heat reservoirs R1 and R2 at temperatures T1 and T2 (such as the stove and the block of ice). If an amount of heat Q flows from R1 to R2, then the net entropy change for the two reservoirs is
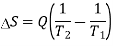
The condition ΔS ≥ 0 determines the maximum possible efficiency of heat engines—that is, systems such as gasoline or steam engines that can do work in a cyclic fashion. Suppose a heat engine absorbs heat Q1 from R1 and exhausts heat Q2 to R2 for each complete cycle. By conservation of energy, the work done per cycle is W = Q1 – Q2, and the net entropy change is ∆S=Q2/T2-Q1/T1
To make W as large as possible, Q2 should be as small as possible relative to Q1. However, Q2 cannot be zero, because this would make ΔS negative and so violate the second law. The smallest possible value of Q2 corresponds to the condition ΔS = 0, yielding (Q2/Q1) MIN=T2/T1as the fundamental equation limiting the efficiency of all heat engines. A process for which ΔS = 0 is reversible because an infinitesimal change would be sufficient to make the heat engine run backward as a refrigerator.
Which is positive provided that T1 > T2. Thus, the observation that heat never flows spontaneously from cold to hot is equivalent to requiring the net entropy change to be positive for a spontaneous flow of heat. If T1 = T2, then the reservoirs are in equilibrium, no heat flows, and ΔS = 0.
Properties of Entropy
- It is a thermodynamic function.
- It is a state function. It depends on the state of the system and not the path that is followed.
- It is represented by S but in the standard state, it is represented by S°.
- It’s SI unit is J/Kmol.
- It’s CGS unit is cal/Kmol.
- Entropy is an extensive property which means that it scales with the size or extent of a system.
- Entropy order: gas>liquid>solids
Entropy Change and Calculations
During entropy change, a process is defined as the amount of heat emitted or absorbed isothermally and reversibly divided by the absolute temperature. Entropy formula is given as.
∆S = qrev,iso/T
If we add the same quantity of heat at a higher temperature and lower temperature, randomness will be maximum at a lower temperature. Hence, it suggests that temperature is inversely proportional to the entropy.
Total entropy change, ∆Stotal =∆Ssurroundings+∆Ssystem
Total entropy change is equal to the sum of entropy change of system and surroundings.If the system loses an amount of heat q at a temperature T1, which is received by surroundings at a temperature T2
So, ∆Stotal can be calculated
∆Ssystem=-q/T1
∆Ssurrounding=q/T2
∆Stotal=-q/T1+q/T2
●If∆Stotal is positive, the process is spontaneous.
●If∆Stotal is negative, the process is non-spontaneous.
●If∆Stotal is zero, the process is at equilibrium.
Entropy changes during the isothermal reversible expansion of an ideal gas
∆S = qrev,iso/T
According to the first law of thermodynamics,
∆U=q+w
For the isothermal expansion of an ideal gas, ∆U = 0
qrev = -wrev = nRTln(V2/V1)
Therefore,
∆S = nRln(V2/V1)
Entropy Change during Reversible Adiabatic Expansion
For an adiabatic process heat exchange will be zero(q=0), therefore reversible adiabatic expansion is taking place at a constant entropy (isentropic),
q = 0
Therefore,
∆S = 0
Even though the reversible adiabatic expansion is isentropic, irreversible adiabatic expansion is not isentropic.
∆S not equal to Zero.
Key takeaways
1) The net entropy change for the two reservoirs is
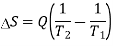
2) Total entropy change, ∆Stotal =∆Ssurroundings+∆Ssystem
3) Temperature. Entropy formula is given as;
∆S = qrev,iso/T
Entropy changes of pure substances
Because most substances' thermodynamic properties are too complex to be expressed by simple equations, they are presented in the form of tables.
Many working fluids can be used in thermo-systems. Water is one of the most commonly used working fluids. This is the only liquid in this section.
The thermodynamic properties that are commonly used are:
- Temperature (T), oC or oF
- Pressure (P), Pa or psia
- Specific volume (v) (the volume per unit mass), m3/kg or ft3/lb
- Specific internal energy (u), kJ/kg or Btu/lb
- Specific enthalpy (h), kJ/kg or Btu/lb
Specific entropy (s) (Which will be introduced in the following section), kJ/(kg-K) or Btu/(lb-R)
Saturated Liquid and Saturated Vapor
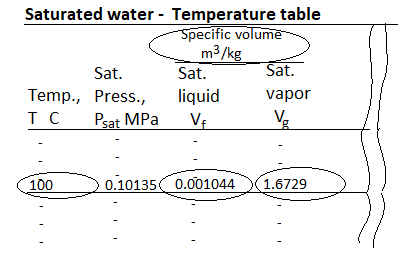
Fig 18 Saturated Water Table
The saturation temperature is the temperature at which a pure substance changes phase at a given pressure. Water has a saturation temperature of 100 oC at 1 atm. The pressure at which a pure substance changes phase at a given temperature is known as the saturation pressure. Water has a saturation pressure of 1 atm at 100 degrees Celsius. The saturation temperature and pressure are interdependent.
There are two kinds of saturated water tables. Both tables contain the same data. The only distinction is that the properties are listed as a function of either temperature or pressure.
The properties listed in the tables include
- Saturation pressure (Psat) for a given temperature or saturation temperature (Tsat) for a given pressure
- Specific volume of saturated liquid (vf) and saturated vapor (vg)
- Specific internal energy of saturated liquid (uf), saturated vapor (ug), and vaporization (ufg = ug - uf)
- Specific enthalpy of saturated liquid (hf), saturated vapor (hg), and vaporization (hfg = hg - hf) or latent heat of vaporization.
Specific entropy of saturated liquid (sf), saturated vapor (sg), and vaporization (sfg = sg - sf)
Saturated Mixture
During the vaporization process of water, the substance is a mixture of saturated liquid and saturated vapor. Quality (x) is defined to describe the fraction of saturated vapor in the mixture.
x = mvapor/mtotal
Where
mvapor = mass of vapor in the mixture
mtotal = total mass of the mixture
mtotal = mliquid + mvapor = mf + mg
Quality is assigned a value between 0 and 1. According to its definition, x equals 1 for saturated vapour and 0 for saturated liquid.
Saturated mixtures are biphasic systems. It can be treated as a homogeneous mixture for convenience, and the properties of this mixture are simply the average properties of the saturated liquid and saturated vapour. For instance, the specific volume of the mixture can be calculated using
Vav = Vf + Vg
mtotal vav = mf vf + mg vg
vav = mf vf/mtotal + mg vg/mtotal
= vf (1 - mg/mtotal) + vg mg/mtotal
= vf (1 - x) + vg x
= vf + vfg x
Rearranging the above equation to give an expression for the quality x as
x = (vav - vf)/vfg
Based on this equation, quality can be determined from the horizontal distance on the T-v or P-v diagram as shown in the figure.
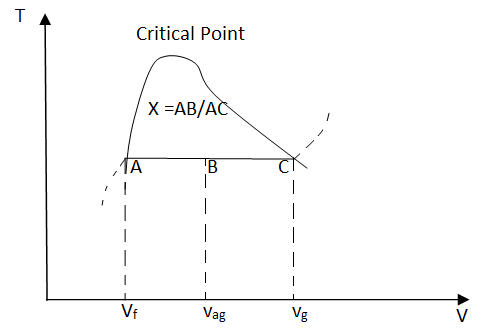
Fig 19 Quality is related to the horizontal distance on T-v diagram
The above process can be repeated for u and h
uav = uf + ufg x
hav = hf + hfg x
Superheated Vapor
Fig 20 Superheated Water Table
Temperature and pressure are independent of each other because superheated vapour is a single-phase substance. The properties of superheated vapours are listed as a function of both temperature and pressure in the superheated vapour tables. Among the properties listed are v, u, h, and s. The saturation temperature for the pressure is given in parentheses after the pressure value.
Superheated vapor can be characterized by
- P <Psat at a given T
- T >Tsat at a given P
- v > vg at a given P or T
- u >ug at a given P or T
h > hg at a given P or T
Sub cooled Liquid
Fig 21 Sub cooled Water Table
The subcooled liquid water tables have the same format as the superheated vapour tables. In the absence of compressed liquid data, it is common practise to estimate the properties of compressed liquid using saturated liquid data based on the given temperature. The following approximation can be used to reduce the error for h.
Subcooled liquid can be characterized by
- P >Psat at a given T
- T <Tsat at a given P
- v <vf at a given P or T
- u <uf at a given P or T
h <hf at a given P or T
The entropy of a pure substance is determined from tables in the same manner as other properties such as v, u, and h. The value of entropy at a specified state is determined just like any other property.
- Compressed liquid: from tables
- Saturated liquid (sf): from tables
- Saturated7 mixture: s = sf + xsfg
Where
x = quality
sfg = sg - sf
- Saturated vapor (sg): from tables
- Superheated vapor: from tables
If the compressed liquid data are not available, the saturated liquid at the same temperature can be used to approximate the compressed liquid's entropy.
From 2nd law,
By, first law for a closed-flow system
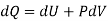
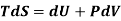
Again, from Enthalpy
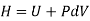
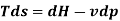
The above two Tds thermodynamic equations relate to properties of the system.
 | Any process and for any system | Reversible & Irreversible |
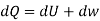 | Any process under closed stationary system |
|
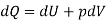 | Closed system when only PdV is present | Reversible (Quasi-static) process |
 |
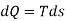| Reversible process |
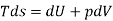 | Any process under closed stationary system | Reversible & Irreversible |
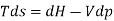 | Relates properties of closed system. It doesn’t have any path function | Holds good for any process |
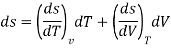
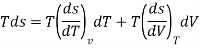
As,
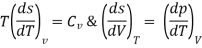
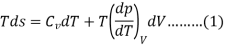
If S=S (T, P)
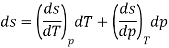
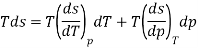
As,
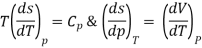
The entropy of the isolated system is a measure of the system's irreversibility. The greater the irreversibility, the greater the entropy of the system. As a result, the reversible process is an ideal process that never occurs in reality. This means that a certain amount of irreversibility is always present in the system, and that the entropy of the isolated system is always increasing, never decreasing. Let us remember that an isolated system can always be formed by combining any system and its surroundings within a single boundary.
“An irreversible process always tends to bring the isolated system into greater disarray. An isolated system always tends to increase in entropy. The entropy of a system can be roughly defined as a measure of the degree of molecular disorder present in the system. When heat is applied to a system, the disorderly motion of the molecules increases, as does the system's entropy. When the heat is removed from the system, the opposite happens.”
The first and second law of thermodynamics can be Summarizing in Clausius two statements:
- The energy of the world (universe) is constant.
- The entropy of the world tends towards a maximum.
As a result, the entropy of the isolated system tends to increase and reaches its maximum value at the point of equilibrium. When the system reaches equilibrium, the entropy increase becomes zero.
Let a system change from state 1 to state 2 by a reversible process A and return to state 1 by another reversible process B. Then 1A2B1 is a reversible cycle. Therefore, the Clausius inequality gives:
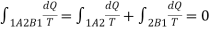
If the system is restored to the initial state from 1 to state 2 by an irreversible process C, then 1A2C1 is an irreversible cycle. Then the Clausius inequality gives:
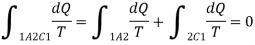
Subtracting the above equation from the first one,
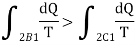
Since the process 2B1 is reversible,
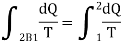
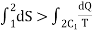
In general
Where the equality sign indicates a reversible process and the inequality sign indicates an irreversible process.
Let us now use the above result to calculate the entropy change of the universe when a system interacts with its surroundings and exchanges energy as heat.
Let Tsur and Tsys be the temperatures of the surroundings and the system such that Tsur >Tsys Let dQ represent the energy transfer as heat from the surroundings to the system during the given irreversible process.
DSsys = dQ/Tsys
DSsur = -dQ/Tsur
DSuni = dSsys + dSsur = (dQ/T) sys - (dQ/T) sur >0
DSuni >0 (since Tsur>Tsys)
If the system is isolated, there is no change in the entropy of the surroundings and DS = 0, for an isolated system. Therefore, the entropy of an isolated system either increases or, in the limit, remains constant.
When the system's process is reversible, the equality sign holds true; when there is any irreversibility in the process, the inequality sign holds true. This is commonly referred to as the principle of entropy increase. Irreversible or spontaneous processes can occur only in the direction that increases the entropy of the universe or an isolated system. These processes cannot occur in a decreasing entropy direction.
For an isolated system,
DS > 0, for irreversible processes
DS = 0, for reversible processes
DS < 0, the process is impossible
Property diagrams are excellent visual aids in thermodynamic process analysis. In previous chapters, we used P-v and T-v diagrams extensively in conjunction with the first law of thermodynamics. It is very useful in the second law analysis to plot the processes on diagrams with entropy as one of the coordinates. The temperature-entropy and enthalpy-entropy diagrams are two commonly used diagrams in second-law analysis. Consider the entropy defining equation (Eq). It can be rearranged as follows:
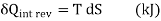…….1
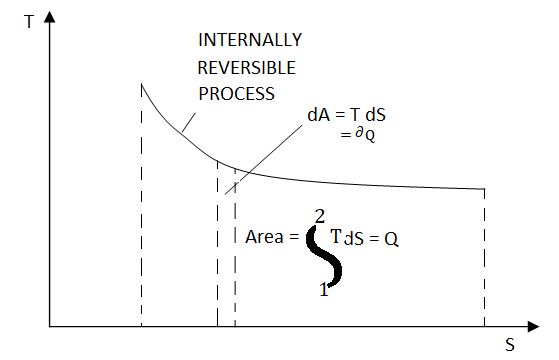
Figure 22 On a T-S diagram
The area under the process curve represents the heat transfer for internally reversible processes.
Equation 1as shown in Fig 17dQrev int corresponds to a differential area on a T-S diagram. The total heat transfer during an internally reversible process is determined by integration to be
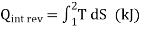….2
Equation 2 denotes the area under the process curve on a T-S diagram. As a result, we conclude that heat transfer during an internally reversible process is represented by the area under the process curve on a T-S diagram. This is similar to the area under the process curve on a P-V diagram representing reversible boundary work. For processes that are internally (or completely) reversible, the area under the process curve represents heat transfer. The term "irreversible processes" has no meaning in this context. Equations 1 and 2 can also be expressed in terms of unit mass as
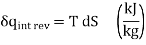
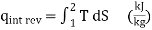…….3,4
To carry out the integrations in Equations 2 and 4, one must first understand the relationship between T and s during a process. The internally reversible isothermal process is one example of a special case in which these integrations are simple. It produces
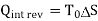(kJ)
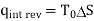(kJ/kg)
5 or 6, where T0 is the constant temperature and S is the system's entropy change during the process. On a T-s diagram, an isentropic process is easily identified as a vertical line segment. This is to be expected because an isentropic process does not involve heat transfer, so the area under the process path must be zero (Fig. 23).
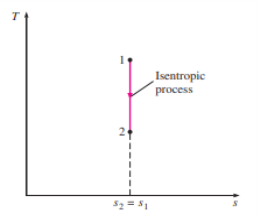
Figure 23 the isentropic process appears as a vertical line segment on a T-s diagram.
T-s diagrams are useful tools for visualising the second-law aspects of processes and cycles and are thus widely used in thermodynamics. The water T-s diagram is shown in the appendix in Fig. A–9. The enthalpy-entropy diagram is another common engineering diagram that is useful in the analysis of steady-flow devices such as turbines, compressors, and nozzles.
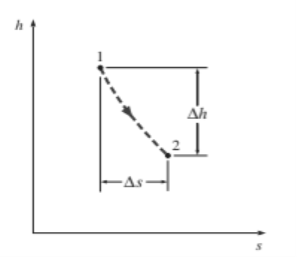
Figure 24 for adiabatic steady-flow devices
The vertical distance h on an h-s diagram represents work, and the horizontal distance s represents irreversibility.
The coordinates of an h-s diagram represent two important properties: enthalpy, which is a primary property in the first-law analysis of steady-flow devices, and entropy, which accounts for irreversibility during adiabatic processes. In analysing the steady flow of steam through an adiabatic turbine, for example, the vertical distance h between the inlet and exit states is a measure of the turbine's work output, and the horizontal distance s is a measure of the process's irreversibility (Fig. 7–18). The h-s diagram is also called a Mollier diagram.
According to 3rd law, the entropy of a perfect crystal at zero Kelvin (Absolute zero) is equal to zero. At absolute zero the system must be in a state with the minimum possible energy.
Zero entropy datum is chosen at 0 C or 275 K
The third law defines an absolute reference point for determination of entropy at any other temperature. The entropy of a perfect crystal lattice is defined by Nernst’s equation.
- Absolute zero Temperature
- Third law is defined by Nernst’s equation
- At absolute zero temp it has minimum energy
References:
- Basic and Applied Thermodynamics by PK Nag, MCGRAW HILL INDIA.
- Thermodynamics for Engineers by Kroos & Potter, Cengage Learning.
- Thermodynamics by Shavit and Gutfinger, CRC Press.
- Thermodynamics- An Engineering Approach by Cengel, MCGRAW HILL INDIA.
- Basic Engineering Thermodynamics, Joel, Pearson.
