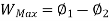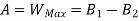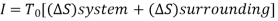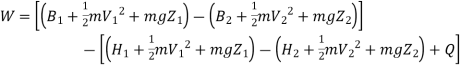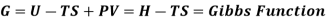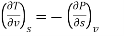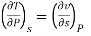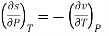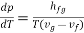Unit – 3
Availability and Irreversibility
According to thermodynamics sources of energy is Classified as High grade & Low-grade energy.
High Grade | Low Grade |
Mechanical Work | Heat or Thermal energy |
Electrical energy | Nuclear fission or fusion |
Water power | Fossil fuels |
Wind power |
|
Kinetic energy of a Jet |
|
Tidal Power |
|
Low grade energy cannot be completely converted into high grade energy by 2nd law of thermodynamics. The part of energy which is left after conversion is known as Available energy.
That rejected energy is called as Unavailable energy.
Key Takeaway:
- The part of energy which is left after conversion is known as Available energy.
- That rejected energy is called as Unavailable energy
Availability:
Availability is defined as the Max useful work which can be obtained during a process in which the system comes in equilibrium with its surroundings.
| Initial Values | Final Values |
Internal Energy | U | U0 |
Entropy | S | S0 |
Volume | V | V0 |
Note:
The heat of the system is being exchanged with the environment, it may be both reversible and irreversible.
Useful work is given by,
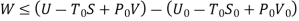
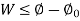
Where,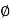 
is availability function, i.e., a composite function of both
System and environment.
Thus, the useful work is ≤ the decrease in the availability function.
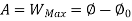
A= Availability
This work is obtained from a decrease in the internal energy of system & heat removed from environment.
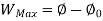
A system has two equilibrium states then,
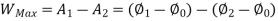
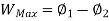
Availability in steady flow:
A mass m is flowing in the system then,
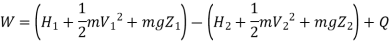
Assuming KE & PE are negligible
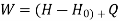
Entropy at entrance & exit = S & 
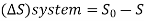
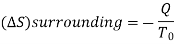
From entropy,
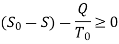
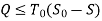
Useful work,
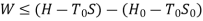
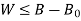
B is called availability function for steady state flow also known as Keenan Function.
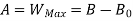
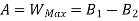
The availability & Unavailable quantity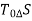 
are also called Energy & Anergy respectively.
Irreversibility:
The work done in idealized Process is always more than actual Process. The difference between these two is called irreversibility (Degradation or Dissipation).
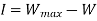
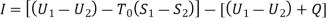
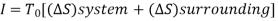
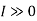
Irreversibility in steady flow:
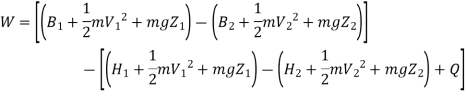
The same expression for irreversibility applies to both flow and non-flow process.
Key Takeaway:
According to the Second Law of Thermodynamics, no real process can be completely isentropic. Or, to put it another way, no real process can use all of the exergy in a system. The goal of engineering is to reduce the generation of entropy. Second-law efficiencies assess how successfully entropy generation has been reduced in a device by comparing real processes to an equivalent idealised isentropic process using thermal efficiencies or COPs: Think of the amount of exergy not used as the energy lost due to the generation of entropy. Engineering aims to maximise the use of exergy. Hence these formulas can be rewritten in terms of exergy:
Heat Engines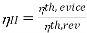 
Fridge/Heat Pump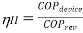 
Work-Producing Device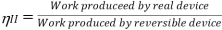 
Work-Consuming Device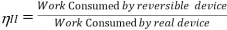 
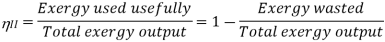
From 1st Law,
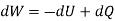
It is assumed that the system exchanges energy only with the environment at Temp T0.
As,
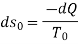
So,
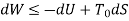
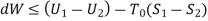
As,
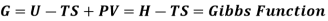
Key Takeaway:
Quantities such as internal energy (U), volume, pressure, and temperature can be used to specify the state of a system, and you've probably heard of entropy (S) and free energy (G). These properties define the system's current state and are independent of how the system arrived at that state. All of these variables are defined as State functions, which are solely dependent on the system's state.
Work (w) and heat (q) are properties that are affected by the path taken between states, which is referred to as a path function.
Differentials of state functions are exact (dP, dV, dG,)
Differentials of Path functions are inexact (dw, dq)
On integration of exact differential, the result depends only on the final and initial points, but not on the path chosen.
But, On integration of an inexact differential, the path will have a huge influence in the result, even if starting and ending points are same.
State Function Examples:
DU=TdS−PdV
DH=TdS+VdP
DA=−SdT−PdV
DG=−SdT+VdP
State Function after differentiation:
DU=T(S,V)dS−P(S,V)dV
DH=T(S,P)dS+V(S,P)dP
DA=−S(T,V)dT−P(T,V)dV
DG=−S(T,P)dT+V(T,P)dP
As the differentials are exact, we can derive a few new relationships like,
As
G=G(T,P)
So,
DG=(∂G∂T)PdT+(∂G∂P)TdP
As,
(∂G∂T)P=−S & (∂G∂P)T=V
Hence,
−(∂S∂P)T=(∂V∂T)P
Some thermodynamic properties can be directly measured, but many others cannot. As a result, some relationships between these two groups must be established in order to evaluate properties that cannot be measured directly. The derivations are based on the fact that properties are point functions and that any two independent, intensive properties can completely specify the state of a simple, compressible system.
Some Mathematical Preliminaries
Thermodynamic properties have exact differentials and are continuous point functions. A property of a single component system can be denoted by the general mathematical function z = z. (x, y). For example, this function could be the pressure P = P. (T, v). The total z differential is denoted as.
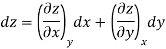
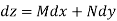
Where
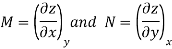
Taking the partial derivative of M with respect to y and of N with respect to x yields.
and 
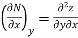
The following is true because properties are continuous point functions with exact differentials.
The Maxwell relations are the equations that relate the partial derivatives of the properties P, v, T, and s of a simple compressible substance to each other. They are calculated using the four Gibbs equations. The first two Gibbs equations are those derived from internal energy u and enthalpy h.
Du= T ds- Pdv
Dh= T ds + v dP
The definitions of the Helmholtz function and the Gibbs function g result in the second two Gibbs equations.
a= u - Ts
Da = du - T ds - sdT
Da = sdT - Pdv
g = h - Ts
Dg = dh – T – ds - sdT
Dg = sdT + v dP
The Maxwell relations are obtained by equalising the second mixed partial derivatives of these four functions.
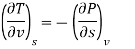
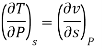
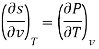
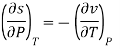
Now we develop two more important relations for partial derivatives—the reciprocity and the cyclic relations. Consider the function z = z (x, y) expressed as x = x (y, z). The total differential of x is
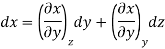
Now combine the expressions for dx and dz.
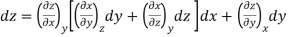
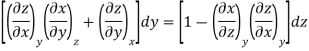
Since y and z are independent of each other, the terms in each bracket must be zero. Thus, we obtain the reciprocity relation that shows that the inverse of a partial derivative is equal to its reciprocal.
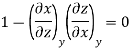
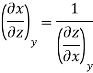
The second relation is called the cyclic relation
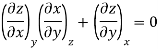
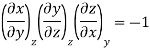
Key Takeaway:
There are three states of matter: solid, liquid, and gas. Only two of these three states can coexist in general equilibrium. Whenever a solid changes into a liquid or a liquid change into a vapour, the temperature remains constant. During the transition from one state to another This temperature, while pressure-dependent, is unique to each substance. When changing from a solid to a liquid state, the characteristic temperature is known as the melting point of the solid, and when changing from a liquid to a vapour state, the temperature is known as the boiling point of the liquid. The melting or boiling point has a specific value at a specific pressure, and vice versa. Using the second law of thermodynamics, it is possible to obtain a relationship showing how melting and boiling points vary with pressure.
The idea is to run a Carnot engine between temperatures and T-dT for a two-phase medium and observe the phase change. The Clausius-Clapeyron equation, which gives the slope of the vapour pressure curve, can then be used to derive an important relationship. We could then measure the slope of the vapour pressure curve for various substances and compare it to the Clausius-Clapeyron equation.
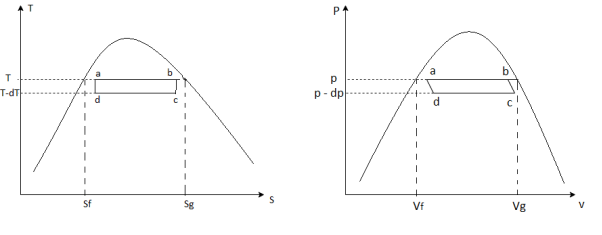
Figure (a) depicts the infinitesimal Carnot cycle abcd (b). Between states a and b, heat is absorbed. The amount of heat required to vaporise an arbitrary amount of mass m.
The system must be supplied with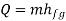 
The thermal efficiency of a Carnot cycle can be calculated using the first and second laws of thermodynamics.
Hence, for the infinitesimal cycle considered above
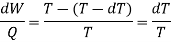
The work along bc and da nearly cancel, so the network is the difference between the work along and ab and cd and dW, which can be represented by the rectangle abcd.
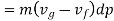
Substituting Equations (1) and (3) into (2) we obtain
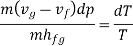
Rearranging terms yields the Clausius-Clapeyron equation, which defines the slope of the vapour pressure curve:
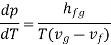
The beauty is that we have discovered a general relationship between experimentally measurable quantities based on first principles (1st and 2nd laws of thermodynamics). Clapeyron's latent heat equation holds true for both liquid-to-vapour and solid-to-liquid state changes. In the latter case, hfg will represent the fusion latent.
Key Takeaway:
There is a pressure drop associated with flow through a restriction like valves, capillary tube, porous plug etc.
• The enthalpy of the fluid remains a constant.
• The temperature of a fluid may increase, decrease, or remain constant during a throttling process.
• The behaviour of fluids in such flows is described by the Joule-Thomson coefficient. The Joule-Thomson coefficient is defined as:
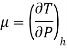
The Joule-Thomson coefficient is a measure of the change in temperature with pressure during a constant-enthalpy process.
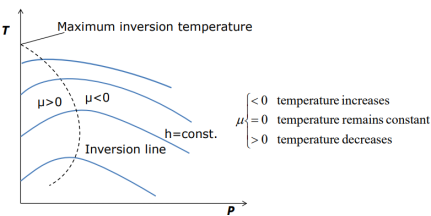
Some h= constant lines on the T-P diagram pass through a point of zero slope or zero Joule-Thomson coefficient
•The line that passes through these points is called the inversion line, and the temperature at a point where a constant-enthalpy line intersects the inversion line is called the inversion temperature.
• The slopes of the h=constant lines are negative (μ0) to the left of the inversion line.
Key Takeaway
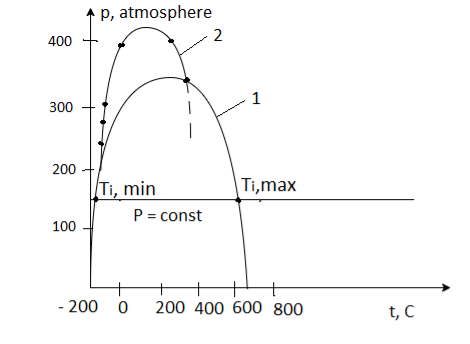
It is a curve defined on a phase diagram that bounds the region of phases (states) of a substance in which the substance transitions from higher pressure to lower pressure (throttling), including temperature drop.
Throttling causes the substance (a gas or liquid) to heat up beyond this region. At the two inversion points (Ti, max), the constant-pressure line (isobar p = constant) intersects the inversion curve (Ti, min). The upper point is in the region of the substance's gaseous state, and the lower point is in the liquid state.
Materials expand when heated by a coefficient of expansion β. It is represented in equation form as,
ΔV = Vo β ΔT
Were,
Change in volume = ΔV
Initial volume = Vo
Coefficient of volume expansion= β
Temperature increase = ΔT
Compressibility β is defined as the reciprocal of bulk modulus (k) and is equal to the fractional change in volume divided by the stress (pressure) applied to the body.
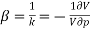(1)
Consider the ideal gas as an example of isothermal and adiabatic compressibility.
For the isothermal process, we have an equation (for one mole of gas for simplicity)
PV= constant
We differentiate this to get
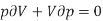
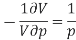
The left-hand side of this expression is isothermal compressibility (see equation (1)). Thus
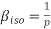
Now we have the equation for adiabatic process
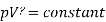
We differentiate this to have
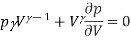
A little rearrangement yields
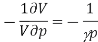
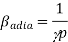
Since is always greateer than 1, therefore from equations (2) and (3) it is clear that
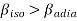
Key Takeaway:
- ΔV = Vo β ΔT
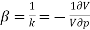
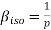
References:
- Basic and Applied Thermodynamics by PK Nag, MCGRAW HILL INDIA.
- Thermodynamics for Engineers by Kroos& Potter, Cengage Learning.
- Thermodynamics by Shavit and Gutfinger, CRC Press.
- Thermodynamics- An Engineering Approach by Cengel, MCGRAW HILL INDIA.
- Basic Engineering Thermodynamics, Joel, Pearson.
