Unit-2
A cam is a mechanical component used for transmitting motion to a follower by direct contact. The driver of the system is known as the cam and the driven oneis called the follower. In a pair of cam and follower, the cam normally rotates, whereas the follower may translate or oscillate. A common example around us is the cam shaft of an automobile engine, where the cams drive the push rods (as the followers) in order to open and close the valves in synchronization with the emotion of the pistons.
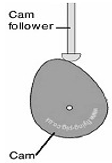
Fig. 1: Cam and follower
Cams are the devices used for converting rotation motion into reciprocating motion. The motion created can be complex or regular and simple and irregular. As the cam rotates, turned by the circular motion, the cam follower traces the surface of the cam transmitting its motion to the required mechanism. The design of cam follower is quite important in the way the profile of the cam is followed. A fine pointed follower will more accurately trace the outline of the cam. This more accurate movement is at the expense of the strength of the camfollower.
2.2.1 Classification of Cams
Cams can be classified based on their physical shape.
Disk or plate cam: The disk (or plate) cam has an irregular contour to impart a specific motion to the follower. The follower moves in a plane perpendicular to the axis of rotation of the cam shaft and is held in contact with the cam by springs or gravity.
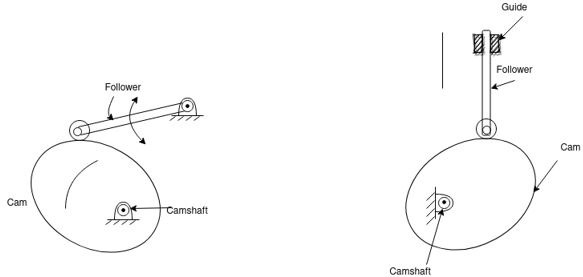
Fig. 2: Disk or plate arm
Cylindrical cam: The cylindrical cam has a groove cut along its cylindrical surface. The roller follows the groove, and the follower moves in a plane parallel to the axis of rotation of the cylinder.
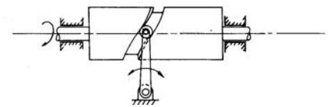
Fig. 3: Cylindrical cam
Translating cam:
The translating cam is a contoured or grooved plates liding on a guiding surface(s). The follower may oscillate (Fig.3 a) or reciprocate (Fig. 3b). The contour or the shape of the groove is determined by the specified motion of the follower.
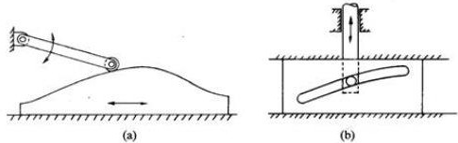
Fig. 4: Translating cam
2.2.2 Classification of Followers
Based on surface in contact
Knife edge
Roller follower
Flat faced
Spherical follower
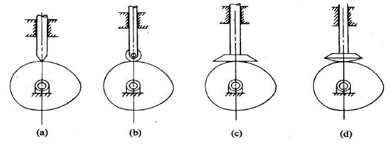
Fig. 5: Follower classification based on surface in contact
Based on type of motion
Oscillating
Translating
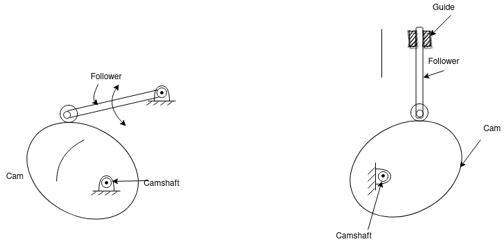
Fig. 6: Follower classification based on type of motion
Based on line of motion
Radial follower: The lines of movement of in-line cam followers pass through the centers of the camshafts.
Off-set follower: For this type, the lines of movement are offset from the centers of the Cam shafts.
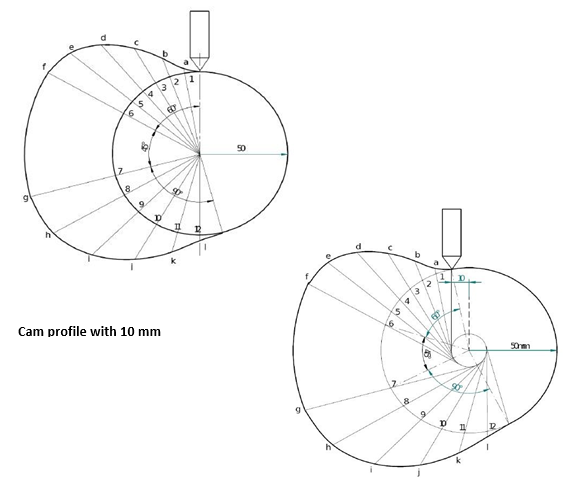
Fig. 7: Classification of cam on the basis of line of motion
Key Takeaway
Based on surface in contact, based on type of motion, Based on line of motion.
When the contacting end of the follower has a sharp knife edge, it is known as knife edge follower. It has limited use as it produces maximum wear. It is having poor performance.
The cam profile for knife edge is shown below:
Example for cam profile for knife edge for following conditions:
Follower type = Knife edged, in-line; lift = 50mm; base circle radius = 50mm; outstroke with SHM, for 60°cam rotation; dwell for 45°cam rotation; return stroke with SHM, for 90° cam rotation; dwell for the remaining period. (2) Draw the cam profile for the same operating condition so f with the follower offset by 10mm to the left of cam center.
Fig. 8: Displacement Diagram for knife edge follower
Cam Profile
Key takeaway
Knife edge follower has limited use as it produces maximum wear that is why it is having poor performance.
2.4.1 For Uniform Velocity
The abscissa represents the time or angular displacement of the cam in degrees. The ordinate represents the displacement, or velocity or acceleration of the follower.
Since the follower moves with uniform velocity during its rise and return stroke, therefore the slope of the displacement curves must be constant. In other words, AB1 and C1D must be straight line.
The periods during which the follower remains at rest are known as dwell periods, as shown by lines B1C and DE as in figure (a).
From fig (c), we see that the acceleration or retardation of the follower at the beginning and at the end of each stroke is infinite. This is due to the fact that the follower is required to start from rest and has to gain velocity within no time.
This is only possible if the acceleration or retardation at the beginning and at the end of each stroke is infinite.
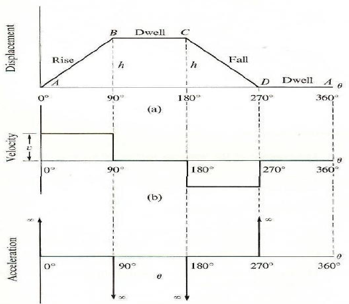
Fig. 9: Displacement, velocity and acceleration diagram for uniform velocity
Follower motion with modified uniform velocity:
It has been observed in the displacement diagrams of the follower of motion with uniform velocity that the acceleration of the follower becomes in finite at the beginning and ending of rise and return strokes. In order to prevent this, the displacement diagrams are slightly modified and in the modified form, the velocity of the follower varies uniformly during the initial stage and at the end of each stroke. Accordingly, the displacement to the follower varies in parabolic pattern during the same periods. The displacement, velocity and acceleration patterns are as shown in fig. 10.
Fig. 10: Diagram for modified uniform velocity
Key Takeaway
The acceleration or retardation of the follower at the beginning and at the end of each stroke is infinite therefore it is necessary to have
Modified diagram of uniform.
2.4.2 For Uniform Acceleration
Divide the angular displacement of the cam during out (φ0) into any number of equal numbers (say eight) and draw the vertical lines through these points as shown in figure below and numbered these points as A, 1,2,3,4,5,6,7and 8.
Divide the vertical passes through point 4 into eight equal parts (height =h=stroke of cam) and numbered as a, b, c, d, e, f, g and h.
Joining point, A to points a, b, c, d to obtain corresponding points B, C, D, and E on the lines passing through 1, 2, 3 and 4 respectively.
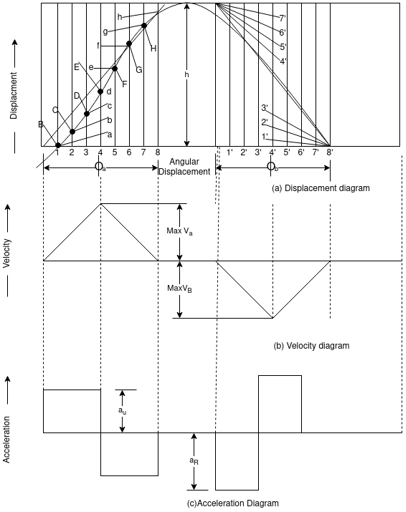
Fig.11: Displacement, velocity and acceleration diagram for uniform acceleration
Similarly joining point J to point’s e, f, and g to obtain corresponding point F, G, and H on the lines passing through 5, 6, and 7 respectively.
Join these points with free hand to draw the required parabolic displacement curve.
Let,h=stroke of the follower, ῳ= Angular velocity of cam, φ0 and φR= Angular displacement during out stroke of the follower.
Time required for the follower during outstroke, t0=φ0/ῳ
Mean stroke of the follower during outstroke, v0=h/t0
Since, the maximum velocity=2*mean velocity
v0=2h/t0 =2ῳh/φ0
As acceleration and deceleration are constant so,
Maximum acceleration=Maximum velocity/Time to attain maximum velocity
From the diagram we see that for attaining the maximum velocity the time required is half of the total time, therefore, maximum acceleration, a0=v0/(t0/2) = 2ῳh/φ0(φ0 / 2ῳ)
Similarly, for return stroke, VR=2ῳh/φR
aR=4ῳ2h/φ2R
NOMENCLATURE OF CAMS
Cam Profile: The contour of the working surface of the cam.
Trace Point: The point at the knife edge of a follower, or the center of a roller, or the center of a spherical face.
Pitch Curve: The path of the tracer point.
Base Circle: The smallest circle drawn, tangential to the cam profile, with its center on the axis of the cam shaft. The size of the base circle determines the size of the cam.
Prime Circle: The smallest circle which can be drawn from the center of the cam and tangent to the pitch curve.
Prime circle radius = Base circle radius for knife edge and flat faced follower.
Prime circle radius = Prime circle radius is the sum of Base circle radius along with radius of roller for roller follower.
Pressure Angle: The angle between the normal to the pitch curve and the direction of Motion of the follower at the point of contact.
Lift of stroke: It is the maximum travel of the follower from its lowest position to the topmost position. The maximum rise is called lift.
Pitch Point: It is a point on the curve having maximum pressure angle.
Pitch Circle: It is the circle drawn from the center of the cam through the pitch points.
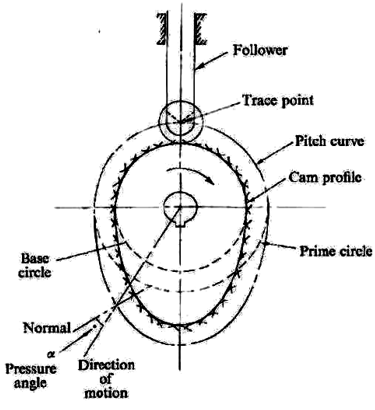
Fig.12: Nomenclature of cam profile
A toothed wheel that engages another toothed mechanism in order to change the speed or direction of transmitted motion.
Fig. 13: Diagram of a gear
A gear is a component within a transmission device that transmits rotational force to another gear or device. A gear is different from a pulley in that a gear is a round wheel which has linkages that mesh with other gear teeth, allowing force to be fully transferred without slippage. Depending on their construction and arrangement, geared devices can transmit forces at different speeds, torques, or in a different direction, from the power source. The most common situation is for a gear to mesh with another gear.
Gear’s most important feature is that gears of unequal sizes (diameters) can be combined to produce a mechanical advantage, so that the rotational speed and torque of the second gear are different from that of the first.
To overcome the problem of slippage as in belt drives, gears are used which produce positive drive with uniform angular velocity.
Key takeaway
A gear is a component within a transmission device that transmits rotational force to another gear or device. A gear is different from a pulley and its functions as well as designs varies from each other.
Gears or toothed wheels may be classified as follows:
According to the position of axes of the shafts, the axes of the two shafts between which the motion is to be transmitted, may be
2.6.1 Spur Gear
Teeth is parallel to axis of rotation can transmit power from one shaft to another parallel shaft. Spur gears are the simplest and most common type of gear. Their general form is a cylinder or disk. The teeth project radically, and with these "straight-cut gears".
Spur gears are gears in the same plane that move opposite of each other because they are meshed together. Gear ‘A’ is called the ‘driver’ because this is turned by a motor. As gear ‘A’ turns it meshes with gear ‘B’ and it begins to turn as well. Gear ‘B’ is called the ‘driven’ gear.
External gear makes external contact, and the internal gear (right side pair) makes internal contact.
APPLICATIONS OF SPUR GEAR
Electrical screwdriver, dancing monster, oscillating sprinkler, windup alarm clock, washing machine and clothes dryer.
2.6.2 Parallel Helical Gear
The teeth on helical gears are cut at an angle to the face of the gear. When two teeth on a helical gear system engage, the contact starts at one end of the tooth and gradually spreads as the gears rotate, until the two teeth are in full engagement.
Fig. 15: Parallel helical gear
This gradual engagement makes helical gears operate much more smoothly and quietly than spur gears. For this reason, helical gears are used in almost all car transmissions. Because of the angle of the teeth on helical gears, they create a thrust load on the gear when they mesh. Devices that use helical gears have bearings that can support this thrust load.
One interesting thing about helical gears is that if the angles of the gear teeth are correct, they can be mounted on perpendicular shafts, adjusting the rotation angle by 90 degrees.
Fig. 16: Parallel helical gear
2.6.3 Herringbone gears
To avoid axial thrust, two helical gears of opposite hand can be mounted side by side, to cancel resulting thrust forces. These are called double helical or herringbone gears
Fig. 17: Herringbone gear
Applications of Herringbone Gears
The most common application is in power transmission. They utilize curved teeth for efficient, high capacity power transmission. This offers reduced pulsation due to which they are highly used for extrusion and polymerization. Herringbone gears are mostly used on heavy machinery.
2.6.4 Rack and pinion
Rack and pinion gears are used to convert rotation (From the pinion) into linear motion (of the rack). A perfect example of this is the steering system on many cars. The steering wheel rotates a gear which engages the rack. As the gear turns, it slides the rack either to the right or left, depending on which way you turn the wheel. Rack and pinion gears are also used in some scales to turn the dial that displays your weight.
Fig. 18: Rack and pinion
GEARS FOR CONNECTING INTERSECTING SHAFTS
1. Straight Bevel Gear
Bevel gears are useful when the direction of a shaft's rotation needs to be changed. They are usually mounted on shafts that are 90 degrees apart, but can be designed to work at other angles as well. The teeth on bevel gears can be straight, spiral or hypoid. Straight bevel gear teeth actually have the same problem as straight spur gear teeth as each tooth engages, it impacts the corresponding tooth all a tonce.
Fig. 19: BEVEL GEAR
Just like with spur gears, the solution to this problem is to curve the gear teeth. These spiral teeth engage just like helical teeth: the contact starts at one end of the gear and progressively spreads across the whole tooth.
Fig.20: SPIRAL BEVEL GEAR
On straight and spiral bevel gears, the shafts must be perpendicular to each other, but they must also be in the same plane. If you were to extend the two shafts past the gears, they would intersect
The bevel gear has many diverse applications such as locomotives, marine applications, automobiles, printing presses, cooling towers, power plants, steel plants, railway track inspection machines, etc.
NON-INTERSECTING AND NON-PARALLEL
WORM AND WORMGEAR
Worm gears are used when large gear reductions are needed. It is common for worm gears to have reductions of 20:1, and even up to 300:1 or greater.
Many worm gears have an interesting property that no other gear set has: the worm can easily turn the gear, but the gear cannot turn the worm. This is because the angle on the worm is so shallow that when the gear tries to spin it, the friction between the gear and the worm holds the worm in place.
Fig.21: Worm and worm gear
This feature is useful for machines such as conveyor systems, in which the locking feature can act as a brake for the conveyor when the motor is not turning. One other very interesting usage of worm gears is in the torsion differential, which is used on some high- performance cars and trucks. They are used in right-angle or skew shaft drives. The presence of sliding action in the system even though results in quieter operation, it gives rise to considerable frictional heat, hence, they need good lubrication for heat dissipation and for improving the efficiency. High reductions are possible which results in compact drive.
Key Takeaway
Gear has been mainly classified into three major categories intersecting gear, non-intersecting and parallel gear.
It states that the common normal at the point of contact between a pair of teeth must always pass through the pitch point.
Proof:
Consider two bodies (1) and (2) representing the portion of the two gears in mesh.
At a point C on the tooth profile gear (1) is in contact with a point D on the tooth profile of gear (2).
Let n-n be the common normal at point C and D on the respective curves.
Let, ῳ1= Instantaneous angular velocity of gear (1),
ῳ2=Instantaneous angular velocity of gear (2)
vc=Linear velocity of C, and vd=Linear velocity of D
Now, vc=ῳ1AC, in direction perpendicular to AC.
vd=ῳ2BD, in direction perpendicular to BD.
As both gears should be in contact so one surface may slide relatives to other along the common normal as it will lead to separation of gear teeth.
Component of vc along n-n= vccosα, Component of vd along n-n= vdcosß
Relative motion along n-n= vccosα-vdcosß
For proper contact: vccosα-vdcosß=0
There are two forms of tooth:
Involute teeth profile:
An involute teeth profile is defined as the locus of a point on a straight line which rolls without slipping on the circumference of a circle. The circle on which the straight lines rolls is known as the base circle.
Let A be the point on a base circle. First divide circle in equal number of parts, example, Ap1=P1P2=P2P3 etc. Draw the tangents at points P1, P2, P3 etc. Cut the length equals to AP1, AP2, and AP3 on the tangents made from points P1, P2 and P3 and mark the points as A1, A2 and A3.
Join all the points, will form an involute teeth profile. For such teeth profile, normal at any point of an involute is a tangent to the base circle.
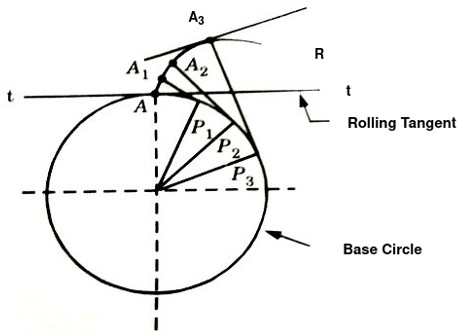
Fig. 22: Involute teeth
Cycloidal Teeth profile:
It is a locus of a point on the circumference of the circle that rolls without slipping on a fixed straight line. When a circle rolls without slipping on the circumference of another circle, the locus of a point on the circle is known as epicyloid. If a circle rolls without slipping inside the circumference of another circle, the locus of the point on the circle is known as hypocycloid.
Let APB is a circle inside which a circle H rolls. When rolling starts, A is the point of contact. As the circle rolls, the locus of point A, gives a path ALP which is hypocloid. A small portion of the curve near the pitch circle is used for the flank of the tooth.
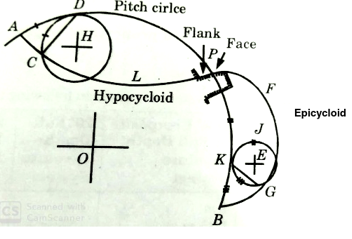
Fig. 23: Cycloidal tooth profile
Let a circle E rotates or rolls outside the pitch circle, then the locus of its point of contact form an epicycloids PFB. A small portion of the curve near the pitch circle is used for the face of the tooth.
The following four systems of gear teeth are commonly used in practice:
The 14.50 composite systems are used for general purpose gears. It is stronger but has no interchange ability. The tooth profile of this system has cycloidal curves at the top and bottom and involute curve at the middle portion.
The tooth profile of the 14.50 full depth involute system was developed for use with gear hobs for spur and helical gears.
The tooth profile of the 200 full depth involute systems may be cut by the hobs. The increase of the pressure angle from14.50 to 200 results in a stronger tooth, because the tooth acting as a beam is wider at the base.
The 200 stub involute systems have a strong tooth to take heavy loads.
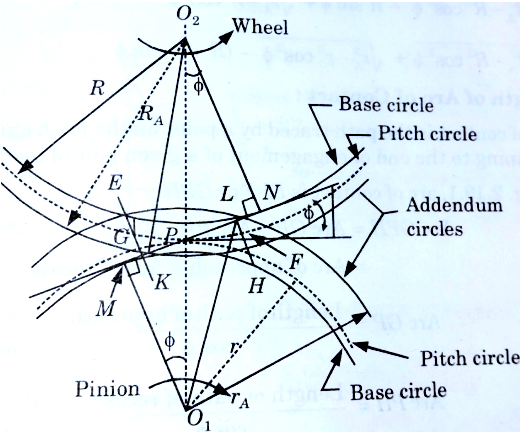
Fig.24: Length of path of contact
Let a pinion with centre O1 driving a wheel with centre O2.
When the pinion rotates in clockwise direction, the contact between a pair of involute teeth begins at K (on the flank near the base circle of pinion) an ends at L (outer end of the tooth face on the pinion).
MN is the common normal at the point of contact as well as acts as common tangent to the base circles.
Hence, KL is the length of path of contact where K is the intersection point of the addendum circle of pinion and common tangent.
From figure given below, KL=KP+PL
=Path of approach + Path of recess
Length of path of contact =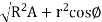 
+
Key takeaway
+
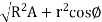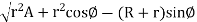, is used to derive length of path of contact.
It is defined as the ratio of the length of the arc of contact to the circular pitch.
Contact ratio=Length of arc of contact/p
Where, p=circular pitch=πm
Minimum number of teeth on the gear wheel to avoid interference:
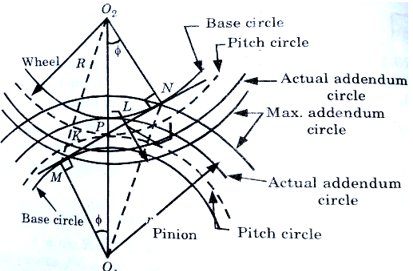
Fig.25: Interference of gear
Let T = Minimum number of teeth required on the wheel to avoid interference.
Aωm = Addendum of the wheel,
Where, Aω= A constant, which is multiplied by module to get addendum of wheel,
m = Module,
R = Pitch circle radius of wheel,
R = mT/2
G = Gear ratio = T/t = R/r, and
Φ = Pressure angle or angle of obliquity.
From ∆O2MP,
(O2M)2 = (O2P)2 + (PM)2 – 2 × O2M × PM cos (∠O2PM)
= R2 + r2 sin2ϕ – 2 Rr sinϕ cos (90° + ϕ )
= R2 + r2 sin2ϕ + 2 Rr sin2ϕ
[ ∵ PM = O1 P sin ϕ = r sin ϕ ]
= R2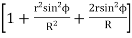
= R2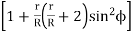
O2M =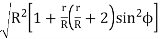 
= mT/2 
[∵ R = mT/2, r/R= t/T = 1/G]
O2M = mT/2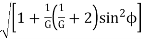 
Addendum of the gear wheel = O2M – O2P
Aωm = mT/2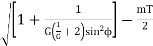 
T =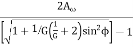
For G = 1, we have
T = 
Key Takeaway
Minimum number of teeth required on the wheel to avoid interference.
T =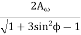 
Minimum number of teeth required on the pinion in order to avoid interference.
Let t = Minimum number of teeth on the pinion required to avoid interference,
Apm = Addendum of the pinion,
Ap = Fraction by which the standard addendum of one module for the pinion should be multiplied to avoid interference, and
r = mt/2 = Pitch circle radius of pinion.
From ∆O1NP, (Refer Figure given),
(O1N)2 = (O1P)2 + (PN)2 – 2O1P × PN cos (∠O1PN)
= r2 + R2 sin2ϕ – 2rR sin ϕ cos ( 90° + ϕ)
= r2 + R2 sin2 ϕ+2rR sin2ϕ
= r2 [1+R2/r2 sin2ϕ + 2R/r sin2ϕ]
= r2 [ 1+ R/r (R/r + 2) sin2ϕ]
= r2 [ 1+ (T/t + 2) T/t sin2ϕ]
O1N = r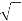 
Addendum of the pinion = O1N – O1P
Apm = mt/2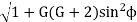 
- mt/2
Apm = mt/2 [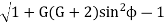 
]
t =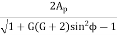 
For G = 1,
= 
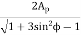
From above result, we concluded that for G =1, both gear and pinion required same number of teeth to avoid interference.
Key Takeaway
t = Minimum number of teeth on the pinion required to avoid interference,
t=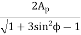
A gear train is two or more gear working together by meshing their teeth and turning each other in a system to generate power and speed. It reduces speed and increases torque. To create large gear ratio, gears are connected together to form gear trains. They often consist of multiple gears in the train. The smaller gears are one-fifth of the size of the larger gear. Electric motors are used with the gear systems to reduce the speed and increase the torque. Electric motor is connected to the driving end of each train and is mounted on the test platform. The output end of the gear train is connected to a large magnetic particle brake that is used to measure the output torque.
Types of gear trains
The most common of the gear train is the gear pair connecting parallel shafts. The teeth of this type can be spur, helical or herringbone. Only one gear for each axis, the angular velocity is simply the reverse of the tooth ratio. The main limitation of a simple gear train is that the maximum speed change ratio is 10:1. For larger ratio, large sizes of gear trains are required. The sprockets and chain in the bicycle is an example of simple gear train. When the paddle is pushed, the front gear is turned and that meshes with the links in the chain. The chain moves and meshes with the links in the rear gear that is attached to the rear wheel. This enables the bicycle to move.
Compound Gear Train
For large velocities, compound arrangement is preferred. Two keys are keyed to a single shaft. A double reduction train can be arranged to have its input and output shafts in a line, by choosing equal center distance for gears and pinions. Two or more gears may rotate about a single axis.
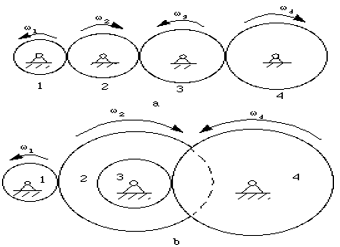
Fig. 26: Simple and compound gear train
Reverted Gear train:
A reverted gear train is one in which the first and the last gear are on the same axis. This arrangement finds its use in speed reducers, clocks to connect hours hand to minutes hand, machine tools etc.
Planetary Gear Train (Epi-cyclic Gear Train)
Planetary gears solve the following problem. Let's say you want a gear ratio of 6:1 with the input turning in the same direction as the output. One way to create that ratio is with the following three-gear train:
Fig. 27: Planetary gear train
In this train, the blue gear has six times the diameter of the yellow gear (giving a 6:1 ratio). The size of the red gear is not important because it is just there to reverse the direction of rotation so that the blue and yellow gears turn the same way. However, imagine that you want the axis of the output gear to be the same as that of the input gear. A common place where this same-axis capability is needed is in an electric screwdriver. In that case, you can use a planetary gear system, as shown here:
In this gear system, the yellow gear (the sun) engages all three red gears (the planets) simultaneously. All three are attached to a plate (the planet carrier), and they engage the inside of the blue gear (the ring) instead of the outside. Because there are three red gears instead of one, this gear train is extremely rugged. The output shaft is attached to the blue ring gear, and the planet carrier is held stationary -- this gives the same 6:1 gear ratio. Another interesting thing about planetary gear sets is that they can produce different gear ratios depending on which gear you use as the input, which gear you use as the output, and which one you hold still. For instance, if the input is the sun gear, and we hold the ring gear stationary and attach the output shaft to the planet carrier, we get a different gear ratio. In this case, the planet carrier and planets orbit the sun gear, so instead of the sun gear having to spin six times for the planet carrier to make it around once, it has to spin seven times. This is because the planet carrier circled the sun gear once in the same direction as it was spinning, subtracting one revolution from the sun gear. So, in this case, we get a 7:1reduction.
You could rearrange things again, and this time hold the sun gear stationary, take the output from the planet carrier and hook the input up to the ring gear. This would give you a 1.17:1 gear reduction. An automatic transmission uses planetary gear sets to create the different gear ratios, using clutches and brake bands to hold different parts of the gear set stationary and change the inputs and outputs.
Planetary gear trains have several advantages. They have higher gear ratios. They are popular for automatic transmissions in automobiles. They are also used in bicycles for controlling power of pedaling automatically or manually. They are also used for power train between internal combustion engine and an electric motor.
Applications
Gear trains are used in representing the phases of moon on a watch or clock dial. It is also used for driving a conventional two-disk lunar phase display off the day-of-the-week shaft of the calendar.
Velocity ratio of Gear trains
We know that the velocity ratio of a pair of gears is the inverse proportion of the diameters of their pitch circle, and the diameter of the pitch circle equals to the number of teeth divided by the diametric pitch. Also, we know that it is necessary for the mating gears to have the same diametral pitch so that to satisfy the condition of correct meshing. Thus, we infer that the velocity ratio of a pair of gears is the inverse ratio of their number of teeth.
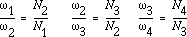
For the ordinary gear trains, we have
These equations can be combined to give the velocity ratio of the first gear in the train to the lastgear:
Epicyclic means one gear revolving upon and around another. The design involves planet and sun gears as one orbit, the other like a planet around the sun. Here is a picture of a typical gear box.
Fig. 29: Sun and planet gear train
References
1.Ghosh Malik, Theory of Mechanism and Machines, East-West Pvt. Ltd.
2. Hannah and Stephans, Mechanics of Machines, Edward Arnolde Publication.
3. R L Norton, Kinematics and Dynamics of Machinery, First Edition, McGraw Hill Education
(India) P Ltd. New Delhi
4. Sadhu Singh, Theory of Machines, Pearson
5. D.K. Pal, S.K. Basu, Design of Machine Tools, Oxford &Ibh Publishing Co Pvt. Ltd.
6. Dr. V. P. Singh, Theory of Machine, Dhanpatrai, and sons.
7. C. S. Sharma & Kamlesh Purohit, “Theory of Machine and Mechanism”, PHI.
8. Mr. C. Ravindran, Department of Mechanical Engineering S.C.E, Vijaya mangalam.
