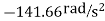Unit - 3
Force Analysis
Equilibrium: A rigid body is said to be in equilibrium if it continues it continues its state of motion
The conditions of equilibrium can be written mathematically as:
∑M=0
∑F=0
Static force Analysis
The analysis is carried out by determining all the forces and couples acting on all the pairs. In this analysis, we ignore the forces due to acceleration. Only the effects of external forces applied to the mechanism are considered.
Necessary conditions for static equilibrium of a body for a planar system:
A body is said to be in static equilibrium if it remains in its state of rest or motion. The necessary conditions of static equilibrium are as follows:
(i) The vector sum of all the forces on body must be zero, that is ∑F=0.
(ii) The vector sum of all the moment about any arbitrary point must be zero, that is, ∑M=0.
If the body is planar or of 2-Dimensional system, motion then the conditions of static of static equilibrium are as follows:
(i) ∑Fx=0, that is, sum of all the horizontal components must be zero.
(ii) ∑Fy=0, that is, sum of all the vertical components must be zero.
(iii) ∑M=0, that is, sum of all the moment about any arbitrary point must be zero.
Key takeaway:
(iii) The vector sum of all the forces on body must be zero, that is ∑F=0.
(iv) The vector sum of all the moment about any arbitrary point must be zero, that is, ∑M=0. For a body to be in a static equilibrium.
Question 1: What are the conditions for a body to be equilibrium under the action of two forces, three forces and two forces and a torque?
Answer: Two forces System- Fig. 1, shows a member under the action of two forces. The body will be equilibrium if
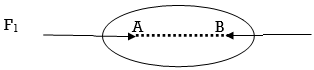
Fig. 1: Two forces System
Three Force Systems: Fig. 2 shows a three forces system. The body will be will be in equilibrium if,
Fig. 2: Three force System
3. These forces intersect at a single point, that point is known as point of concurrency.
Two Forces and a torque System:
Let us consider a link that is hinged at its one end and free to rotate about the hinged point.
A force F1 is acting at free end, and a force F2, is acting at the hinged point and a torque T is acting on the link in clockwise sense.
The system will be in equilibrium if,
The forces are equal in magnitude and parallel to each other with opposite direction that is F1=F2.
These forces form a couple which is equal and opposite to the applied torque that is,
F1h=F2h=T
Key takeaway:
F1h=F2h=T is the important formula for two forces and torque system during static equilibrium for equal and opposite torque.
Inertia: It is a property of matter by virtue of which a body resists any change in its states, either rest or motion.
It states that “the inertia force and couples, the external forces and torques on a body together give statical equilibrium”.
Inertia Force, Fi=-ma
Inertia Couples Ci=-Igα, where,
m= Mass of body,
a= Acceleration of centre of mass of body.
Ig= Moment of inertia about an axis passing through the centre of mass and perpendicular to plane of rotation of body.
α= Angular acceleration of the body.
Let, F1, F2, F3= External forces acting on the body, and
T1, T2, T3 = External torques on the body about its centre of mass.
Now, according to the principle, ∑F+Fi=0, and ∑T+Ci=0.
The above equations are similar to the equation of body in static equilibrium.
Equivalent offset inertia force: Equivalent offset inertia force is the inertia force which produces joint effect of inertia force and inertia couple that is, an equivalent offset inertia force is used to replace inertia force and inertia couple.
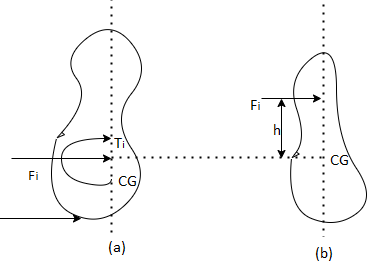
Fig.3: Equivalent Inertia Force
Equivalent offset inertia force can be found by displacing the line of action of inertia force from the centre of mass by a perpendicular displacement h such that the torque so produced is equal to the inertia couple acting on the body.
From the fig. 4, it is clear that Fi acting at a distance h from CG of the body produces same effect as the effect is produced by Fi and Ti,
That is Ti=Couple produced by force Fi
Ti= Ci,
Fi *h = Ci
h = Ci/Fi
Key takeaway: “The inertia force and couples, the external forces and torques on a body together give statical equilibrium”. This is statement is the statement of principle and given by the formula. ∑F+Fi=0, and ∑T+Ci=0
Question 2: The crank of a slider crank mechanism rotates at constant speed of 250 rpm. The crank is 150 mm and the connecting rod is 500 mm long. Determine the angular velocity and the angular acceleration of the connecting rod at the crank angle of 45 degree from the inner dead centre position.
Answer:
Given : N=250 rpm ,r=150mm=0.15 m, l=500mm=0.5 m, 
=45
To find i. Angular velocity
ii. Angular acceleration
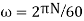
2. We know that
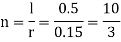
3. Now, angular velocity of connection rod is.
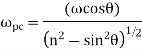
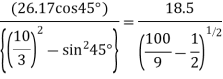
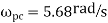
4. Angular acceleration of connecting rod,
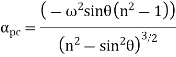
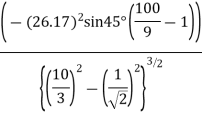
A rigid body is an idealization of a body that does not deform or change shape. Formally it is defined as a collection of particles with the property that the distance between particles remains unchanged during the course of motions of the body. Like the approximation of a rigid body as a particle, this is never strictly true. All bodies deform as they move. However, the approximation remains acceptable as long as the deformations are negligible relative to the overall motion of the body.
A rigid body executes plane motion when all parts of the body move in parallel planes. It follows that all particles in a rigid body moves in a circular paths about the axis of rotation, and all lines in the body in which are perpendicular to the axis of rotation rotate through the same angle in the same time.
We can use Newton’s equations for particles to derive equations of motion of a rigid body. A rigid body which is constrained to move in a plane, has three degrees of freedom, and hence it has three independent equations of motion which relates the forces in the plane to accelerations.
Dynamic force analysis is the evaluation of input forces or torques and joint forces, considering motion of member.
The dynamic analysis of a planar mechanism reveals all the joint reaction forces, including the driving torque required to generate a prescribed steady state motion. It is well known that by D’ Alembert principle, a dynamic problem can be converted into static problem.
(i) Piston Effort: Piston effort is defined as the net or effective force applied on the piston.
Let A1=Area of cover end
A2= Area of piston rod end
P1=Pressure on the cover end, and
P2 = Pressure on the rod end
M= mass of the reciprocating parts.
Force on piston due to gas pressure
Fg= p1A1-p2A2
Inertia force, Fi=m×r×ῳ2[cosθ+(cos 2θ)/n]
Inertia force is in opposite direction of the acceleration of the piston
If a friction force Ff is present then, Net effective force on the piston, F=Fg-Fi-Ff
In a vertical engine, the weight of position also acts on the piston, hence net effective force on the piston, F= Fg+mg-Fi-Ff
(ii) Force along the connecting Rod:
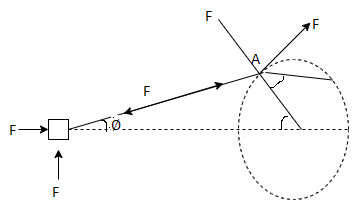
Fig. 4: Force along connecting rod
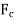
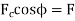
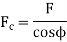
3. Thrust on the sides of cylinder:
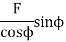
4. Crank pin efforts and crank effort
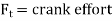
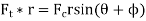
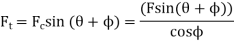
iii. Crank effort,
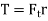
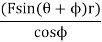
5. Thrust on the bearing
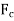
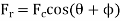
Key Takeaway:
Force on piston due to gas pressure Fg= p1A1-p2A2, Inertia force, Fi=m×r×ῳ2[cosθ+(cos 2θ)/n] are important formulas during designing of piston.
T=Ft*r
=F/cosß[sin(θ+ß)]
=Fr/cosß[sinθ cosß +cosθ sinß]
=Fr[(sinθ+cosß) (sinθ/n)(1/√(1/n(n2-sin2θ)]
=Fr[sinθ+(sin2θ)/2
Also, r sin(θ+ß)=OD cosß
T=Ft*r
=F/cosß[rsin(θ+ß)]
The turning moment diagram (also known as crank-effort diagram) is the graphical representation of the turning moment or crank-effort for various positions of the crank. It is plotted on cartesian co-ordinates, in which the turning moment is taken as the ordinate and crank angle as abscissa.
3.7.1 Turning Moment Diagram for a Single Cylinder Double Acting Steam Engine
A turning moment diagram for a single cylinder double acting steam engine is shown in Fig. 16.1. The vertical ordinate represents the turning moment and the horizontal ordinate represents the crank angle.
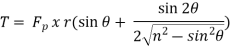
We know that the turning moment on the crankshaft is written as:
From the above expression, we see that the turning moment (T) is zero, when the crank angle (θ) is zero. It
The turning moment in crank shaft is maximum when the crank angle is 90° and it is again zero when crank angle is 180°.
This is shown by the curve abc in Fig. given above and it represents the turning moment diagram for outstroke. The curve cde is the turning moment diagram for in stroke and is somewhat similar to the curve abc.
Since the work done is the product of the turning moment and the angle turned, therefore the area of the turning moment diagram represents the work done per revolution. In actual practice, the engine is assumed to work against the mean resisting torque, as shown by a horizontal line AF. The height of the ordinate a represents the mean height of the turning moment diagram. Since it is assumed that the work done by the turning moment per revolution is equal to the work done against the mean resisting torque, therefore the area of the rectangle a AFe is proportional to the work done against the mean resisting torque.
3.7.2 Turning Moment Diagram for a Four Stroke IC Engine
A turning moment diagram for a four-stroke cycle internal combustion engine is shown in Fig. We know that in a four-stroke cycle internal combustion engine, there is one working stroke after the crank has turned through two revolutions, i.e.720° (or 4 π radians).
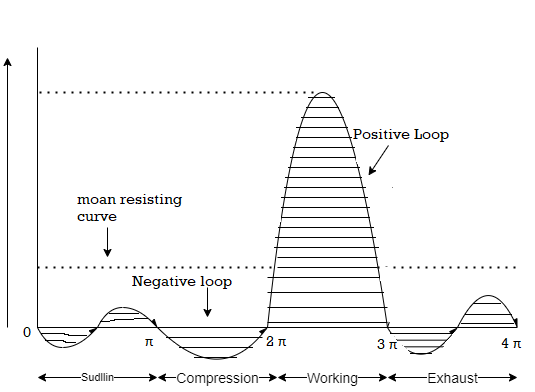
Fig. 6: Turning moment diagram for a four-stroke cycle internal combustion engine.
Since the pressure inside the engine cylinder is less than the atmospheric pressure during the suction stroke, therefore a negative loop is formed as shown in Fig. 16.2. During the compression stroke, the work is done on the gases, therefore a higher negative loop is obtained. During the expansion or working stroke, the fuel burns and the gases expands, therefore a large positive loop is obtained. In this stroke, the work is done by the gases. During exhaust stroke, the work is done on the gas, therefore a negative loop is formed. It may be noted that the effect of the inertia forces on the piston is taken into account in Fig.6.
3.7.3 Turning Moment Diagram for a Multi-cylinder Engine
A separate turning moment diagram for a compound steam engine having three cylinders and the resultant turning moment diagram is shown in Fig. The resultant turning moment diagram is the sum of the turning moment diagrams for the three cylinders. It may be noted that the first cylinder is the high pressure cylinder, second cylinder is the intermediate cylinder and the third cylinder is the low pressure cylinder. The cranks, in case of three cylinders, are usually placed at 120° to each other.
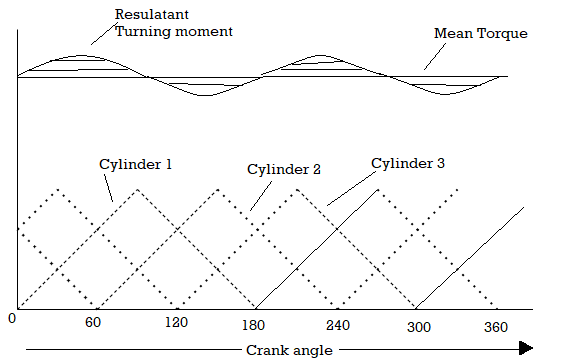
The fluctuation of speed can be defined as the variation in speeds of device or object (crank shaft) during a cycle and the difference between the maximum and minimum speeds during a cycle is called the maximum fluctuation of speed.
LetN1 and N2 = Maximum and minimum speeds in r.p.m. during the cycle, and
N =mean speed in r.p.m =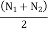 
Coefficient of fluctuation of speed.
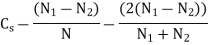
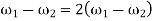
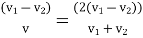(in terms of linear speeds)
The coefficient of fluctuation of speed is a limiting factor in the design of flywheel. It varies depending upon the nature of service to which the flywheel is employed.
In case of steam engines, internal combustion engines, reciprocating compressors and pumps, the energy is developed during one stroke and the engine is to run for the whole cycle on the energy produced during this one stroke. For example, in internal combustion engines, the energy is developed only during expansion or power stroke which is much more than the engine load and no energy is being developed during suction, compression and exhaust strokes in case of four stroke engines and during compression in case of two stroke engines. The excess energy developed during power stroke is absorbed by the flywheel and releases it to the crankshaft during other strokes in which no energy is developed, thus rotating the crankshaft at a uniform speed. A little consideration will show that when the flywheel absorbs energy, its speed increases and when it releases energy, the speed decreases. Hence a flywheel does not maintain a constant speed, it simply reduces the fluctuation of speed. In other words, a flywheel controls the speed variations caused by the fluctuation of the engine turning moment during each cycle of operation.
In machines where the operation is intermittent like *punching machines, shearing machines, riveting machines, crushers, etc., the flywheel stores energy from the power source during the greater portion of the operating cycle and gives it up during a small period of the cycle. Thus, the energy from the power source to the machines is supplied practically at a constant rate throughout the operation.
Energy Stored in a fly wheel:
A flywheel is shown in Fig. We have discussed in that when a flywheel absorbs energy, its speed increases and when it gives up energy, its speed decreases.
Let m= Mass of the flywheel in kg,
k = Radius of gyration of the flywheel in meters
I = Mass moment of inertia of the flywheel about its axis of rotation in kg -
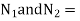maximum and minimum speeds during the cycle in r.p.m
N =mean speed during the cycle in r.p.m =
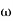= mean angular speed during the cycle in r.p.m =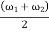
= coefficient of fluctuation of speed =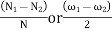 
We know that the mean kinetic energy of the fly wheel.
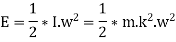
As the speed of the fly wheel changes from 
the maximum fluctuation of energy.
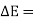maximum K.E – minimum K.E
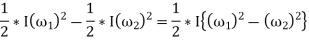
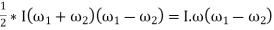-------1
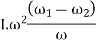
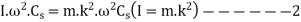
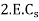(in N- m or joules) 
Expression for Dimensions of Flywheel:
D= mean diameter of rim.
R= mean radius of rim.
A= cross- sectional area of rim.
P= density of rim material
N = speed of flywheel
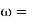Angular velocity of flywheel.
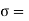Tensile (or hoop) stress due to centrifugal force , and
V= linear velocity at the mean radius.
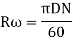
2. Consider a small element of rim which subtends an angle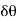 
at the centre of the flywheel.
3. Volume of the small element and, mass of the small element = AR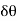 
Dm=Density ×volume
=
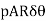
4. Centrifugal force that acts radially outwards
=
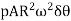
5. Vertical component of dF= dF sin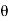 
= 
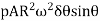
6. Total vertical upward force tending to burst the rim across the diameter XY,
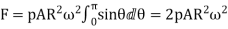………1
7. This vertical upward force will produce hoop stress (or centrifugal stress or circumferential stress) and it is resisted by 2p , such that
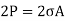…………….2
8. On equating eq. (1)and eq. (2)
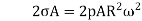
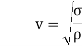
the mass of rim, m= volume × density
=
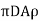
Using equations (1) and (2), we can find the value of the mass radius and cross- sectional area of the rim.
If the cross- sectional area of the rim is rectangular then,
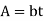, where
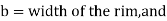
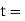Thickness of the rim
Key takeaway:
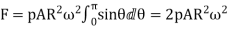and 
are important formulas while expressing the dimensions of a flywheel.
The fluctuation of energy may be determined by the turning moment diagram for one complete cycle of operation. Consider the turning moment diagram for a single cylinder double acting steam engine as shown in Fig. 16.1. We see that the mean resisting torque line AF cuts the turning moment diagram at points B, C, D and E. When the crank moves from a to p, the work done by the engine is equal to the area aBp, whereas the energy required is represented by the area aABp. In other words, the engine has done less work (equal to the area a AB) than the requirement. This amount of energy is taken from the flywheel and hence the speed of the flywheel decreases. Now the crank moves from p to q, the work done by the engine is equal to the area pBbCq, whereas the requirement of energy is represented by the area pBCq. Therefore, the engine has done more work than the requirement. This excess work (equal to the area BbC) is stored in the flywheel and hence the speed of the flywheel increases while the crank moves from p toq.
Similarly, when the crank moves from q to r, more work is taken from the engine than is developed. This loss of work is represented by the area C c D. To supply this loss, the flywheel gives up some of its energy and thus the speed decreases while the crank moves from q to r. As the crank moves from r to s, excess energy is again developed given by the area D d E and the speed again increases. As the piston moves from s to e, again there is a loss of work and the speed decreases. The variations of energy above and below the mean resisting torque line are called fluctuations of energy. The areas BbC, CcD, DdE, etc. represent fluctuations of energy.
A little consideration will show that the engine has a maximum speed either at q or at s. This is due to the fact that the flywheel absorbs energy while the crank moves from p to q and from r to s. On the other hand, the engine has a minimum speed either at p or at r. The reason is that the flywheel gives out some of its energy when the crank moves from a to p and q to r. The difference between the maximum and the minimum energies is known as maximum fluctuation of energy.
Determination of Maximum Fluctuation of Energy
A turning moment diagram for a multi-cylinder engine is shown by a wavy curve in Fig. The horizontal line A G represents the mean torque line. Let a1, a3, a5 be the areas above the mean torque line and a2, a4 and a6 be the areas below the mean torque line. These areas represent some quantity of energy which is either added or subtracted from the energy of the moving parts of the engine.
Let the energy in the flywheel at A = E, then from Fig. , we have Energy at B = E + a1
Energy at C = E + a1– a2
Energy at D = E + a1 – a2 + a3 Energy at E = E + a1 – a2 + a3 – a4
Energy at F = E + a1 – a2 + a3 – a4 + a5 Energy at G = E + a1 – a2 + a3 – a4 + a5 – a6
= Energy at A (i.e. cycle repeats after G)
Let us now suppose that the greatest of these energies is at B and least at E.
Expression for maximum fluctuation of energy
Let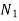 
= maximum speed during the cycle.
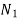= minimum speed during the cycle.
N = mean speed of flywheel =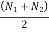
And 
= co-efficient of fluctuation of speed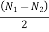 
The mean kinetic energy of the flywheel
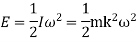
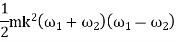
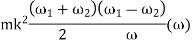
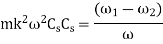
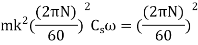
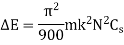
Key takeaway:
The difference between the maximum and the minimum energies is known as maximum fluctuation of energy and this formula is very useful while calculating maximum fluctuation of energy,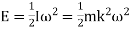 
References
1. Ghosh Malik, Theory of Mechanism and Machines, East-West Pvt. Ltd.
2. Hannah and Stephans, Mechanics of Machines, Edward Arnolde Publication.
3. R L Norton, Kinematics and Dynamics of Machinery, First Edition, McGraw Hill Education (India) P Ltd. New Delhi
4. Sadhu Singh, Theory of Machines, Pearson
5. D.K. Pal, S.K. Basu, Design of Machine Tools, Oxford &Ibh Publishing Co Pvt. Ltd.
6. Dr. V. P. Singh, Theory of Machine, Dhanpatrai, and sons.
7. C. S. Sharma & Kamlesh Purohit, “Theory of Machine and Mechanism”, PHI.
8. Mr. C. Ravindran, Department of Mechanical Engineering S.C.E, Vijayamangalam.
