UNIT 2
Projections of Planes
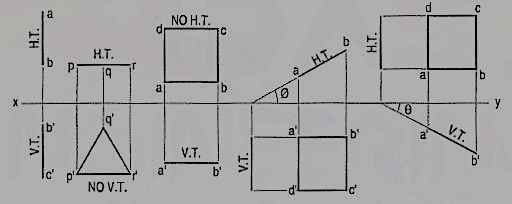
Perpendicular to both the reference planes (fig 1):
A square ABCD is perpendicular to both the planes. Its H.T. And V.T. Are in a straight-line perpendicular to xy.
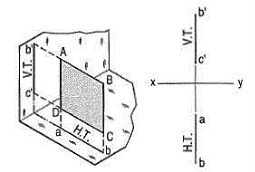
The front view b'c' and the top view ab of the square are both lines coinciding with the V.T. And the H.T. Respectively.
Perpendicular to one plane and parallel to the other plane:
a) Plane, perpendicular to the H.P. And parallel to the V.P. [fig. 12-2(i)]. A triangle PQR is perpendicular to the H.P. And is parallel to the V.P. Its H.T. Is parallel to xy. It has no V.T.
The front view p'q'r' shows the exact shape and size of the triangle. The top view pqr is a line parallel to xy. It coincides with the H.T.
(b) Plane, perpendicular to the V.P. And parallel to the H.P. [fig. 12-2(ii)]. A square ABCD is perpendicular to the V.P. And parallel to the H.P. Its V.T. Is parallel to xy. It has no H.T.
The top view abed shows the true shape and true size of the square. The front view a'b' is a line, parallel to xy. It coincides with the V.T.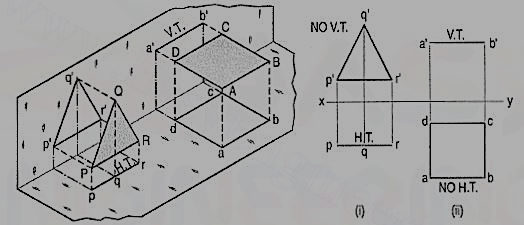
Perpendicular to one plane and inclined to the other plane:
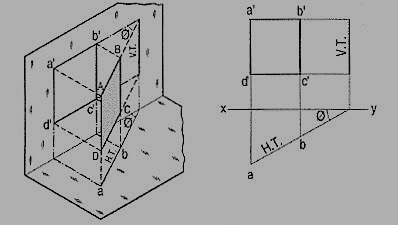
A square ABCD is perpendicular to the H.P. And inclined at an angle φ to the V.P. Its V.T. Is perpendicular to xy. Its H.T. Is inclined at φ to xy.
Its top view ab is a line inclined at φ to xy. The front view a'b'c'd' is smaller than ABCD.
(b) Plane, perpendicular to the V.P. And inclined to the H.P. (fig. 12-4).
A square ABCD is perpendicular to the V.P. And inclined at an angle θ to the H.P. Its H.T. Is perpendicular to xy. Its V.T. Makes the angle e with xy. Its front view a'b' is a line inclined at θ to xy. The top view abed is a rectangle which is smaller than the square ABCD.
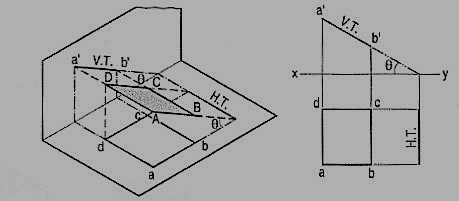
Fig. 36 shows the projections and the traces of all these perpendicular planes by third-angle projection method.
Projection of planes parallel to one of the reference planes:
The projection of a plane on the reference plane parallel to it will show its true shape. Hence, beginning should be made by drawing that view. The other view which will be a line, should then be projected from it.
Note: When the plane is parallel to the H.P.: The top view should be drawn first, and the front view projected from it.
Problem:
An equilateral triangle of 50 mm side has its V.T. Parallel to and 25mm above xy. It has no H.T. Draw its projections when one of its sides is inclined at 45° to the V.P.
As the V.T. Is parallel to xy and as there is no H.T. The triangle is parallel to the H.P. Therefore, begin with the top view.
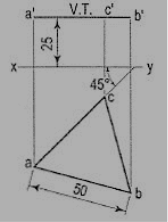
(i) Draw an equilateral triangle abc of 50 mm side, keeping one side, say ac, inclined at 45° to xy.
(ii) Project the front view, parallel to and 25 mm above xy, as shown in fig. 7.
When the plane is parallel to V.P.
Beginning should be made with the front view and the top view projected from it.
Problem:
A square ABCD of 40 mm side has a corner on the H.P. And 20 mm in front of the V.P. All the sides of the square are equally inclined to the H.P. And parallel to the V.P. Draw its projections and show its traces.

As all the sides are parallel to the V.P., the surface of the square also is parallel to it. The front view will show the true shape and position of the square.
(i) Draw a square a'b'c'd' in the front view with one corner in xy and all its sides inclined at 45° to xy.
(ii) Project the top view keeping the line ac parallel to xy and 30 mm below it. The top view is its H.T. It has no V.T.
Projections of planes inclined to one reference plane and perpendicular to other:
When a plane is inclined to a reference plane, its projections may be obtained in two stages. In the initial stage, the plane is assumed to be parallel to that reference plane to which it must be made inclined. It is then tilted to the required inclination in the second stage.
1) Plane, Inclined to the H.P. And perpendicular to the V.P.:
When the plane is inclined to the H.P. And perpendicular to the V.P., in the initial stage, it is assumed to be parallel to the H.P. Its top view will show the true shape. The front view will be a line parallel to xy. The plane is then tilted so that it is inclined to the H.P. The new front view will be inclined to xy at the true inclination. In the top view the corners will move along their respective paths (parallel to xy).
Problem:
A regular pentagon of 25 mm side has one side on the ground. Its plane is inclined at 45° to the H.P and perpendicular to the V.P. Draw its projections and show its traces.
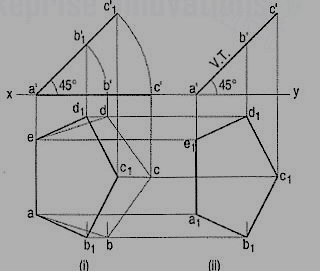
Assuming it to be parallel to the H.P.
(i) Draw the pentagon in the top view with one side perpendicular to xy [fig. 9 (i)]. Project the front view. It will be the line a'c' contained by xy.
(ii) Tilt the front view about the point a', so that it makes 45° angle with xy.
(iii) Project the new top view ab1c1d1e upwards from this front view and horizontally from the first top view. It will be more convenient if the front view is reproduced in the new position separately and the top view projected from it, as shown in fig. 9 (ii). The V.T. Coincides with the front view and the H.T. Is perpendicular to xy, through the point of intersection between xy and the front view-produced.
2) Plane, inclined to the V.P. And perpendicular to the H.P.:
In the initial stage, the plane may be assumed to be parallel to the V.P. And then tilted to the required position in the next stage.
Problem:
Draw the projections of a circle of 50 mm diameter, having its plane vertical and inclined at 30° to the V.P. Its center is 30 mm above the H.P. And 20 mm in front of the V.P. Show also its traces.
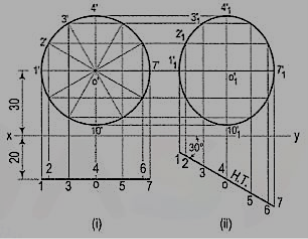
A circle has no corners to project one view from another. However, many points, say twelve, equal distances apart, may be marked on its circumference.
(i) Assuming the circle to be parallel to the V.P., draw its projections. The front view will be a circle [fig. 10 (i)], having its center 30 mm above xy. The top view will be a line, parallel to and 20 mm below xy.
(ii) Divide the circumference into twelve parts (with a 30°-60° set- square) and mark the points as shown. Project these points in the top view. The centre O will coincide with the point 4.
(iii) When the circle is tilted, to make 30° angle with the V.P., its top view will become inclined at 30° to xy. In the front view all the points will move along their respective paths (parallel to xy). Reproduce the top view keeping the centre o at the same distance, viz. 20 mm from xy and inclined at 30° to xy [fig. 10 (ii)].
(iv) For the final front view, project all the points upwards from this top view and horizontally from the first front view. Draw a freehand curve through the twelve points 1'1, 2'1 etc. This curve will be an ellipse.
Projection of oblique planes:
When a plane has its surface inclined to one plane and an edge or a diameter or a diagonal parallel to that plane and inclined to the other plane, its projections are drawn in three stages.
(1) If the surface of the plane is inclined to the H.P. And an edge (or a diameter or a diagonal) is parallel to the H.P. And inclined to the V.P.,
(i) in the initial position the plane is assumed to be parallel to the H.P. And an edge perpendicular to the V.P.
(ii) It is then tilted to make the required angle with the H.P. As already explained, its front view in this position will be a line, while its top view will be smaller in size.
(iii) In the final position, when the plane is turned to the required inclination with the V.P., only the position of the top view will change. Its shape and size will not be affected. In the final front view, the corresponding distances of all the corners from xy will remain the same as in the second front view.
If an edge is in the H.P. Or on the ground, in the initial position, the plane is assumed to be lying in the H.P. Or on the ground, with the edge perpendicular to the V.P. If a corner is in the H.P. Or on the ground, the line joining that corner with the center of the plane is kept parallel to the V.P.
(2) Similarly, if the surface of the plane is inclined to the V.P. And an edge (or a diameter or a diagonal) is parallel to the V.P. And inclined to the H.P.,
(i) in the initial position, the plane is assumed to be parallel to the V.P. And an edge perpendicular to the H.P.
(ii) It is then tilted to make the required angle with the V.P. Its top view in this position will be a line, while its front view will be smaller in size.
(iii) When the plane is turned to the required inclination with the H.P., only the position of the front view will change. Its shape and size will not be affected. In the final top view, the corresponding distances of all the corners from xy will remain the same as in the second top view.
If an edge is in the V.P., in the initial position the plane is assumed to be lying in the V.P. With an edge perpendicular to the H.P. If a corner is in the V.P., the line joining that corner with centre of the plane is kept parallel to the H.P.
Problem:
1. A square ABCD of 50 mm side has its corner A in the H.P., its diagonal AC inclined at 30° to the H.P. And the diagonal BO inclined at 45° to the V.P. And parallel to the H.P. Draw its projections.
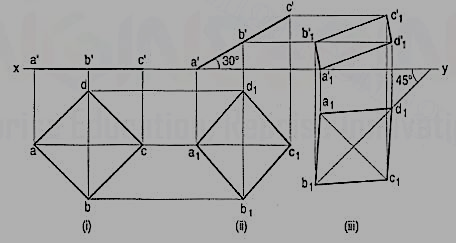
In the initial stage, assume the square to be lying in the H.P. With AC parallel to the V.P.
(i) Draw the top view and the front view. When the square is tilted about the corner A so that AC makes 30° angle with the H.P., BO remains perpendicular to the V.P. And parallel to the H.P.
(ii) Draw the second front view with a'c' inclined at 30° to xy, keeping a' or c' in xy. Project the second top view. The square may now be turned so that BO makes 45° angle with the V.P. And remains parallel to the H.P. Only the position of the top view will change. Its shape and size will remain the same.
(iii) Reproduce the top view so that b1d1 is inclined at 45° to xy. Project the final front view upwards from this top view and horizontally from the second front view.
2. Draw the projections of a circle of 50 mm diameter resting in the H.P. On a point A on the circumference, its plane inclined at 45° to the H.P. And
(a) the top view of the diameter AB making 30° angle with the V.P.;
(b) the diameter AB making 30° angle with the V. P.

Draw the projections of the circle with A in the H.P. And its plane inclined at 45° to the H.P. And perpendicular to the V.P. [fig. 12(i) and fig. 12(ii)].
(a) In the second top view, the line a1b1 is the top view of the diameter AB. Reproduce this top view so that a1b1 makes 30° angle with xy [fig. 12(iii)]. Project the required front view.
(b) If the diameter AB, which makes 45° angle with the H.P., is inclined at 30° to the V.P. Also, its top view a1b1 will make an angle greater than 30° with xy. This apparent angle of inclination is determined as described below.
Draw any line a1b2 equal to AB and inclined at 30° to xy [fig. 12(iv)]. With a1 as center and radius equal to the top view of AB, viz. a1b1, draw an arc cutting rs (the path of B in the top view) at b3. Draw the line joining a1 with b3, and around it, reproduce the second top view. Project the final front view. It is evident that a1b3 is inclined to xy at an angle ϕ which is greater than 30°.
3. A thin 30°-60° set-square has its longest edge in the V.P. And inclined at 30° to the H.P. Its surface makes an angle of 45° with the V.P. Draw its projections.
In the initial stage, assume the set-square to be in the V.P. With its hypotenuse perpendicular to the H.P.
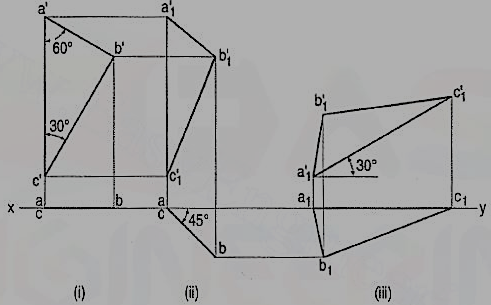
(i) Draw the front view a'b'c' and project the top view ac in xy.
(ii) Tilt ac around the end a so that it makes 45° angle with xy and project the front view a'1b'1c'1.
(iii) Reproduce the second front view a'1b'1c'1 so that a'1b'1 makes an angle of 30° with xy. Project the final top view a1b1c1.
Reference:
- Engineering Drawing Dhananjay A.Jolhe Tata McGraw Hill Education.
- Engineering Drawing Basant Agarwal C.M Agarwal Tata McGraw Hill Education
- Engineering Drawing M.B.Shah, B.C. Rana Pearson Education, India
- A Text book of Engineering Graphics M.I. Dhabhade Association of Technical Authors, Pune.