UNIT-3
Complex Numbers with Application
A number of the form a+ib is known as complex number, where ‘a’ and ‘b’ are two real numbers and i(iota) = 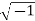 .
.
In a complex number ‘a’ is the real part and ‘b’ is the imaginary part.
If a = 0 , then the imaginary number becomes pure imaginary, same as b = 0 then the number becomes real.
A complex number is always denoted by ‘z’.
The real part of a complex number is denoted by R(z) and imaginary part is denoted by I(z).
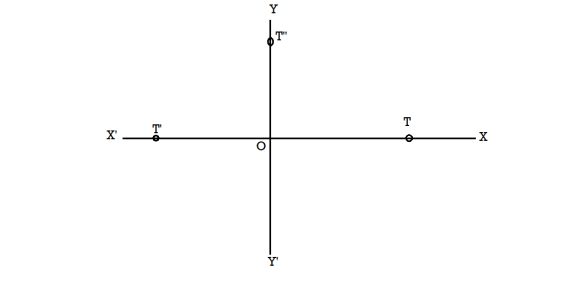
Geometrical representation of imaginary numbers-
Suppose OT is a positive number which is ‘x’ and OT’ = -x
And,
-x = (-1)x = (i)²x = i(ix) which is on OX’.
It represents that the multiplication of the real number x by ‘i’ twice gives to the rotation of OT through two right angles to reach OT’.
That means, the multiplication of x by ‘i’ is equivalent to the rotation of x through one right angle to reach OT’’.
Therefore y-axis (ordinate) is known as an imaginary axis.
Geometric representation of a complex number-
Geometric representation of a complex number is explained by Argand diagram.
Consider axis X’OX and Y’OY are perpendicular to each other with all the positive real numbers along OX and negative real axis along X’O.
As we read above the multiplication of the real number by i is equivalent to the rotation of its direction through 90 degree.
So that all the positive imaginary numbers along OY and negative imaginary number along OY’.
Suppose there is a point M on OY represent the number iy.
Make the rectangle OLPM , so that the Cartesian co-ordinate (x,y) represent a complex number z = x + iy.
The diagram which represent a complex number ‘z’ geometrically is called Argand’s diagram.
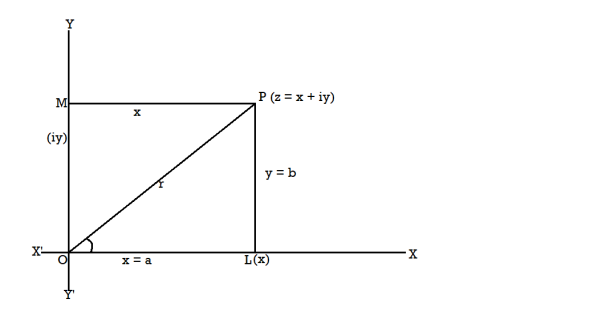
The distance OP is the modulus and the angle is argument of x+iy.
Properties of complex numbers-
1. Equality of complex numbers-
Suppose we have two complex numbers 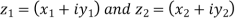 , then these two numbers will be equal only if their real and imaginary parts are equal.
, then these two numbers will be equal only if their real and imaginary parts are equal.
Such that, if 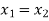 and
and 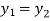 are equal then
are equal then 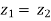 .
.
2. Sum of complex numbers-
Suppose we have two complex numbers 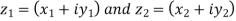 , then their sum will be,
, then their sum will be,
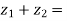
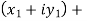
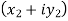 =
= 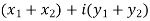
= X + iY , which is complex number.
3. Difference of complex numbers-
Suppose we have two complex numbers 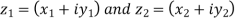 , then their difference will be,
, then their difference will be,
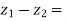
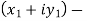
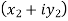 =
= 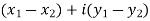
= X - iY , which is complex number.
4. Product of complex numbers-
Suppose we have two complex numbers 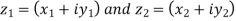 , then their product will be,
, then their product will be,
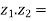
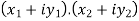 =
= 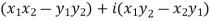 - which is complex number.
- which is complex number.
5. Division of complex numbers-
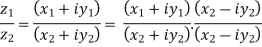
= 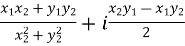 - which is complex number.
- which is complex number.
Note- every complex number can be written in the polar form as-
z = r(cos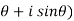
Real and imaginary parts are-
R(z) = r cos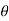 - real part I(z) = r sin
- real part I(z) = r sin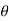 - Imaginary part
- Imaginary part
Here 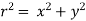 and angle
and angle 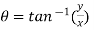
Here , r = 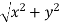 , which is called the modulus of the complex number z = (x+iy) and denoted by |z|.
, which is called the modulus of the complex number z = (x+iy) and denoted by |z|.
Angle 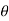 is known as argument of the complex number.
is known as argument of the complex number.
Example: Multiply 3+4i by 3-2i.
Sol. Suppose 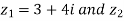 = 3-2i then
= 3-2i then
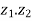 = (
= (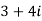 )( 3-2i)
)( 3-2i)
= 9 – 6i + 12i – 8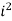
= 9 – 6i + 12i – 8(-1)
= 9 + 6i + 8
= 17 + 6i
Example: If x = cos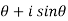 , then prove that 1 +
, then prove that 1 + 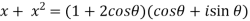
Sol. Here we are given,
x = cos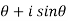 , then
, then
1 + 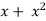 = 1 + (cos
= 1 + (cos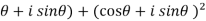
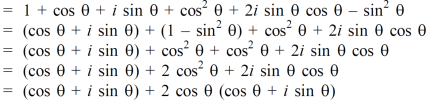
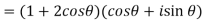
Hence proved.
Example: If x = cos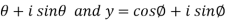 , then prove that,
, then prove that,
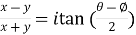
Sol. We are given,
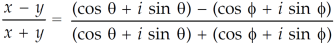

On solving we get,
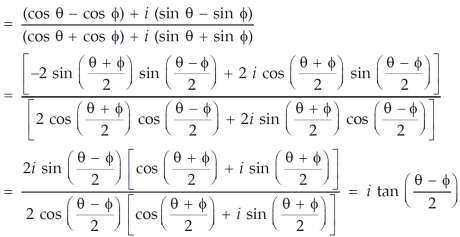
Standard form of a complex number is x + iy.
Conjugate of a complex number-
Suppose we have a complex number z = x +iy , then its conjugate will be
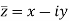
That means , when two complex numbers with different signs of imaginary parts are called conjugate of each other.
Note- the sum and product of a complex number and its conjugate complex are both real.
Example: conjugate complex of z = 3 + 5i is 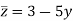
Modulus and Argument of a complex number-
Suppose we have a complex number z = x + iy , then changing its coordinates to polar coordinates,
Put x = r cosθ and y = r sinθ , r = 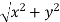 ,
,
Then cosθ = 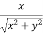 and sinθ=
and sinθ= 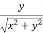
When we take the positive value of root, then this values is called modulus or absolute value of the complex number x + iy and its is denoted by |x + iy|
And angle θ is called argument or amplitude of the complex numver z and denoted by arg.z
The value of θ lies between –π to +π . Which is called the principal value of argument.
There are three types of complex numbers-
1. In Cartesian form – z = x + iy
2. In polar form - z = r(cos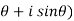
3. In exponential form - r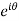
Note-
If we have two complex numbers 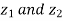 then-
then-
1. |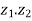 |= |
|= |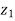 ||
||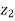 | and amp(
| and amp(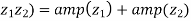
2. 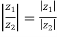 and
and 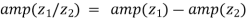
3. |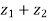 |
|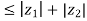
4. |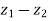 |
|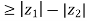
5. |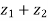 |² +|
|² +|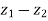 |² = 2(|
|² = 2(|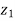 |² + |
|² + |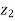 |²)
|²)
Example-1: Find out the modulus and principal argument of the following complex number-
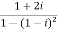 .
.
Sol. Here we have,
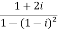
Now, 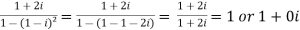
Then, |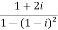 | = |1 + 0i| =
| = |1 + 0i| = 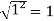
Now, we know that the principal argument is 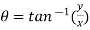
Principal argument of 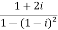 = principal arg of 1 + 0i
= principal arg of 1 + 0i
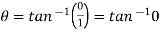 =
= 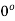
Therefore, modulus = 1 and argument = 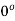
Example-2: If 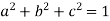 and b + ic = (1 + a)z , then prove that
and b + ic = (1 + a)z , then prove that
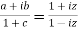
Sol. It is given that,
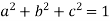 and b + ic = (1 + a)z
and b + ic = (1 + a)z
We can write the second condition as-
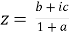
Using right hand side,
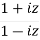 =
= 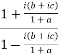
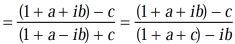
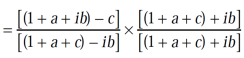
It becomes,
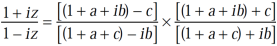
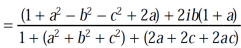
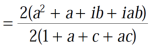
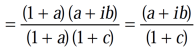
Example-3: If arg(z+1) = π/6 and arg (z – 1) = 2π/3 , then find the complex number.
Sol. Let us suppose, the complex numver is
z = x + iy ……………..(1)
Then,
z+1 = (x+1) + iy
The argument is also given,
Arg(z+1) = 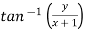 = π/6
= π/6
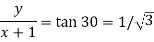
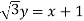 ……………(1)
……………(1)
Now,
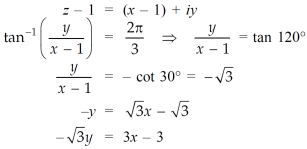
Adding this result with equation (1), we get,
0 = 4x – 2
4x = 2
X = ½
Put the value in (1), we get
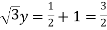
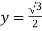
Therefore we got the values of x and y-
Put these values in (1) , we will get the complex number-
z = 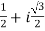
Which is the required complex number.
Example-4: If 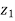 and
and 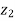 are two complex numbers and |
are two complex numbers and |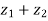 |= |
|= |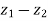 | then show that
| then show that
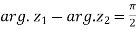
Sol. Let us suppose, two complex numbers are-
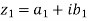
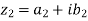
But it is given that,
|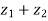 |= |
|= |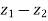 |, put the values , we get
|, put the values , we get
|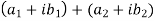 | = |
| = |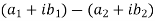 |
|
|(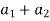 )+i(
)+i(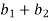 )| = |(
)| = |(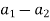 ) + i(
) + i(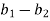 )|
)|
(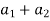 )² + (
)² + (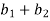 )² = (
)² = (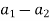 )² + (
)² + (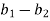 )²
)²
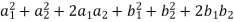 =
= 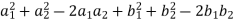
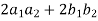 =
= 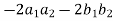
It becomes,
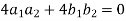
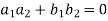 ……………………….(1)
……………………….(1)
Now,
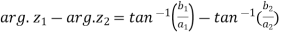
= 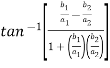
= 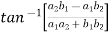
From equation-1:
= 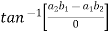 = =
= = 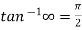
So that,
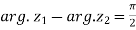
We can define De’Moivre’s theorem as-
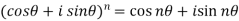
Proof: Let’s prove it by using exponential function-
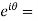 (
(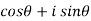 )
)
Put power of ‘n’ on both sides, we get,
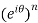 =
= 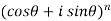
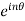 =
= 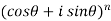
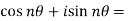
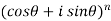 .
.
Example-1: Prove that
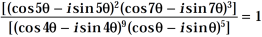
Sol. Here we will use De’Moivre’s theorem,
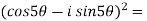
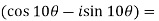
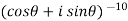
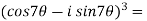
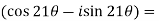
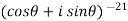
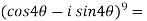
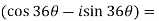
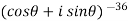
Put these values in LHS,
= 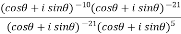 =
= 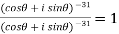
Example-2: Evaluate 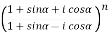
Sol. As we know that from trigonometry,
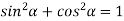
Or,
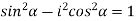 as
as 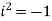
Or,
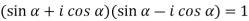 …………. (1)
…………. (1)
Add 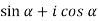 on both sides of eq. (1) , we get
on both sides of eq. (1) , we get
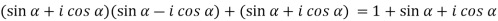
(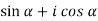 )(
)(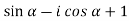 ) =
) = 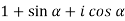
(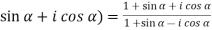
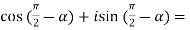
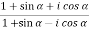
Or
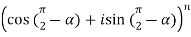 =
= 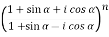
Which becomes,
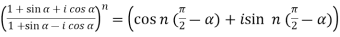 Ans.
Ans.
Example-3: Prove that
1. 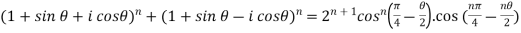
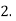
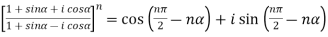
Sol. 1.
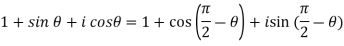
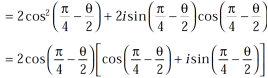
Similarly, we get
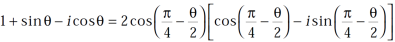
So that
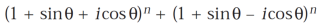
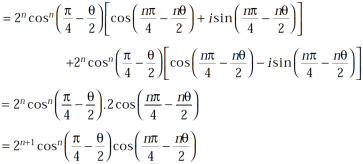
Using the above results, we will solve the second condition-
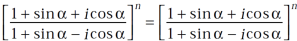
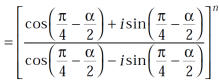
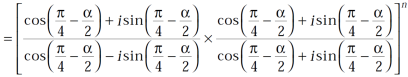
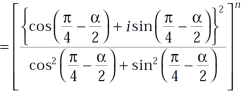
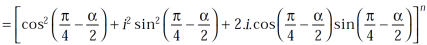
Use 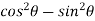 =
= 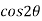 and
and 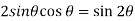 , we get
, we get
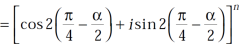
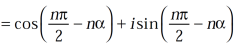 hence proved
hence proved
As we know that 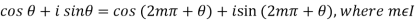
The root of a complex number-
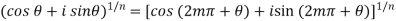
= 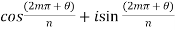
Put m = 0 , 1 , 2 ,,,, n-1 , we get the following values of 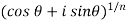
Put m = 0, 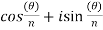
Put m = 1, 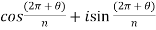
Put m = 2, 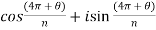
Put m = 3, 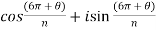
Put m = n – 1, 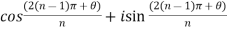
Put m = n , 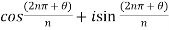 which can be written as –
which can be written as –
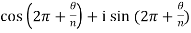
Or
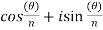
Here we notice that we got the same values for m = 0 and m = n. So that the values for m = n , n+1 , n+2 will be the repetition of the first n values we already obtained.
Example-1: Solve 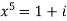 , also find the continued product of the roots.
, also find the continued product of the roots.
Sol. Here we have,
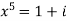
= 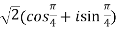
Then,
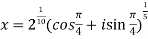
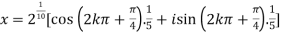
= 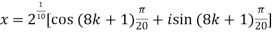
We will obtain the roots by putting k = 0 , 1 , 2 ,3,4….
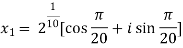

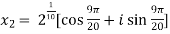

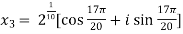

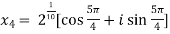

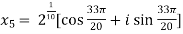
Now find the product of all these,
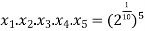
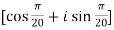 .
.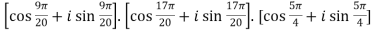 .
.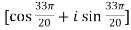
= 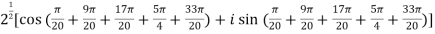
= 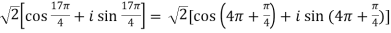
= 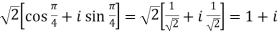 .
.
Example-2: Find the equations whose roots are given below-
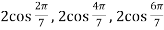
Sol. Let y = 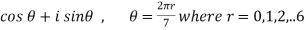 …………….(1)
…………….(1)
Then 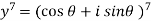
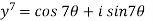
Implying 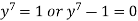
(y-1)(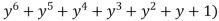 =0 ………..(2)
=0 ………..(2)
Ignoring the factor ( y – 1) , we get
(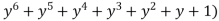 =0 ………. (3)
=0 ………. (3)
Its roots will be,
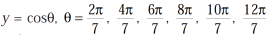
Divide equation-3 , we get
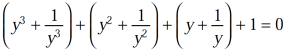
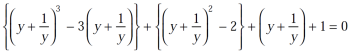
Let x = (y + 1/y) = 2 cosθ then 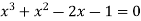 ……….. (4)
……….. (4)
Since, the repeated roots are-
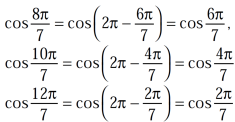
Hence the roots of equation (4) are-
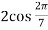 ,
, 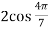 ,
, 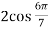 ,
,
Circular function-
As we already know,
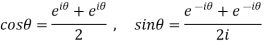
So that, we can define the circular functions of a complex variable z by-

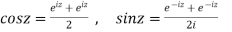
Hyperbolic function-
Hyperbolic functions are-
1. 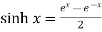 4.
4. 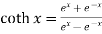
2. 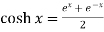 5.
5. 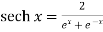
3. 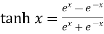 6.
6. 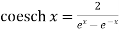
7. 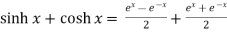 =
= 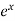
8. 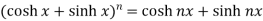
Some important formulae for hyperbolic functions-
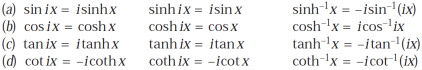
And others are-
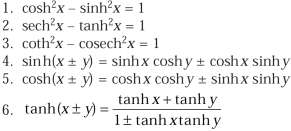
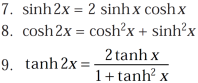
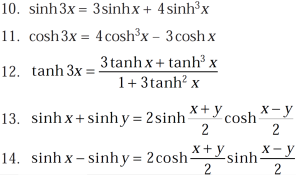
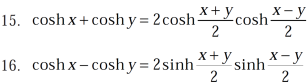
Example-1: prove that
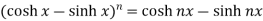
Sol. Here first we will take LHS-
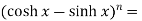
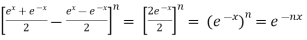 ……….(1)
……….(1)
Now , RHS
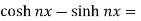
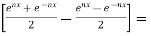
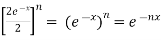
Therefore,
LHS = RHS
Example-2: If 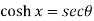 , then prove that
, then prove that
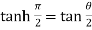
Sol. We have,
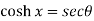
Put the value of cosh x, we get
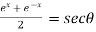
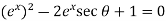
Solving the quadratic equation –
We get the value of 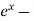
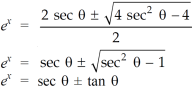
Now for the value of 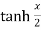 -
-
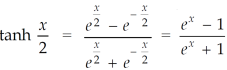
Using the above values, we get
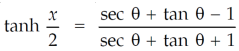
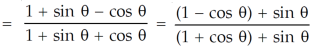
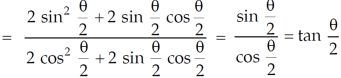
Hence proved
Example-3: If 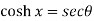 , then prove that
, then prove that
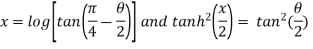
Sol. 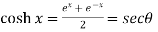 becomes on solving further-
becomes on solving further-
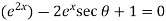
On solving the quadratic equation, we get
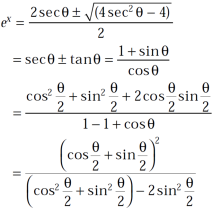
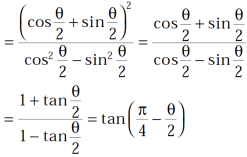
Implying,
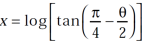
Now, 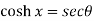 implies-
implies-
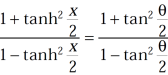 …………………(1)
…………………(1)
Since,

Then by using componendo and dividendo
Equation-1 becomes,
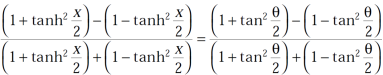
That means,
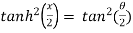
The relation between circular and hyperbolic functions is-
1. 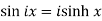
2. 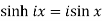
3. 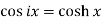
4.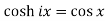
5.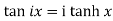
6. 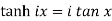
Example: If 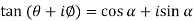 , then prove that-
, then prove that-
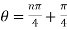
Sol. Here we are given,
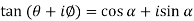
So that,
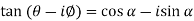
But,
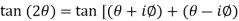
Using trigonometric formulae,
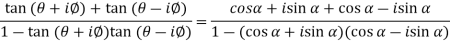
= 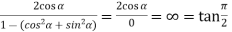
So that,
2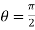
For general values,
2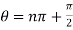 which is
which is
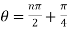
Suppose we have 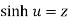 , then u can be written as-
, then u can be written as- 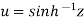 .
.
We can defined other functions too. Like- 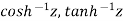
Important results-
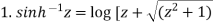
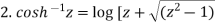
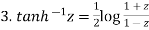
Example-1: Prove that 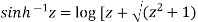
Sol. Suppose 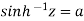 then
then 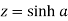
And,
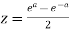
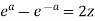
Or,
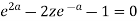
On solving the quadratic equation, we get-
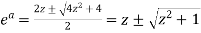
Then,
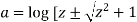 ]
]
Or,
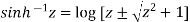
Hence proved.
Example-2: Prove that 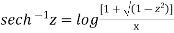
Sol. Suppose 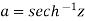 then
then 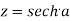
Here 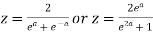
It becomes,
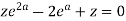
Solving quadratic equation-
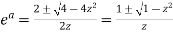
Take positive sign only-
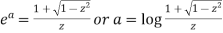
Or we can write-
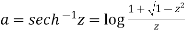 . hence proved.
. hence proved.
Similarly we can prove the results for other functions.
Example-3: Prove that 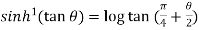
Sol. Using the formula- 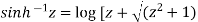
We get,
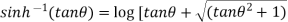
=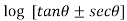
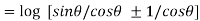
=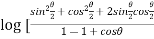 ]
]
= 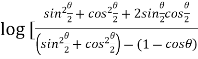 ]
]
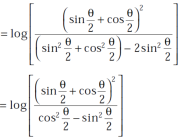
Take cos
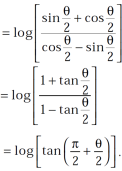
Hence proved.
Separation of real and imaginary parts of circular functions-
1. 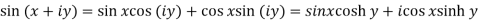
2. 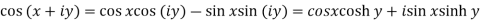
3.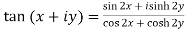
Example-1: If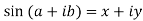 , then prove that-
, then prove that-
1. 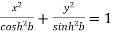
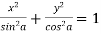
Sol. We know that,
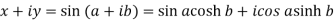
Equating the real and imaginary parts-
x = 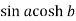 and y =
and y = 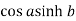
Then,
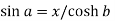 and
and 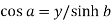
Squaring and adding the above two results, we get-
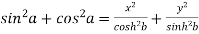
Which is-
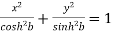 proved.
proved.
Now for second function-
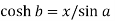 and
and 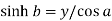
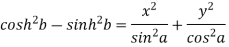
Which becomes-
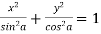
Example-2: If 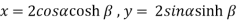 , then prove that-
, then prove that-
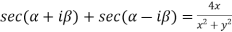
Sol. We take left hand side-
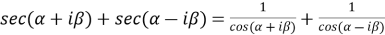
= 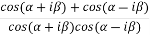
= 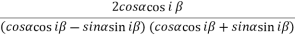
=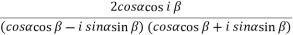
= 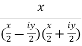
= 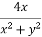
Hence proved
Separation of real and imaginary parts of hyperbolic functions-
1. 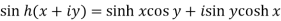
2. 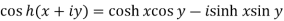
3.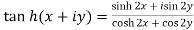
Example-3: If 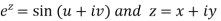 , then prove that-
, then prove that-
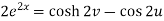
Sol. We have,
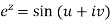
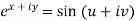

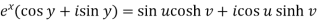
Equating real and imaginary parts-
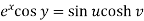 ………………..(1)
………………..(1)
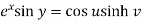 ……………………..(2)
……………………..(2)
Squaring and adding these two equations, we get
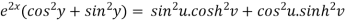
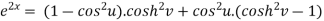
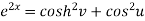
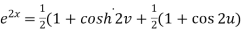
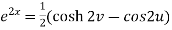
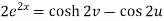
Suppose we have two complex numbers ‘z’ and ‘w’
And 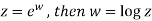
Similarly if , 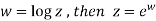
The general value of log z is defined by-
Log z = log z + 2nπi
Example-1: Show that for real values of a and b-
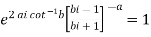
Sol. Let us consider-
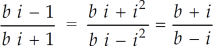
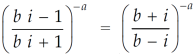
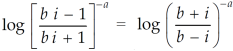
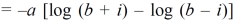
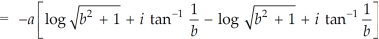
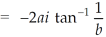
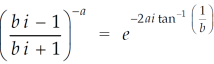
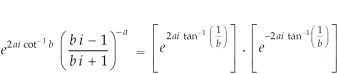
Which is equals to 1.
Example-2: Show that 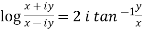
Sol. Suppose,
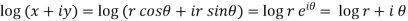
Same as-
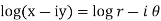
Put these value in LHS, we get
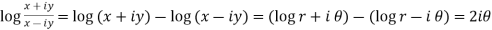
= 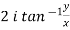
Hence proved.
Example-3: If 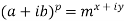 , then prove that
, then prove that 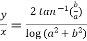
Sol. Here we have,
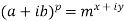
Taking log on both sides,
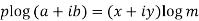
Implying,
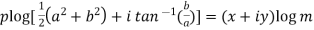
Equating real and imaginary parts-
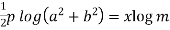 ………………. (1)
………………. (1)
And,
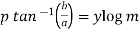 ……………………(2)
……………………(2)
Divide equation(2) by (1), we get
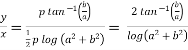
Hence proved.