UNIT-4

REDUCTION FORMULAE AND CURVE TRACING

4.1 Reduction formula

A formula of the form,

= g(x) +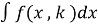

Where k<n, is called a reduction formula.

(a). Reduction formula for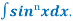                               

Let,                 Iⁿ = 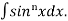   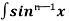 =  sinxdx , if n>1

Taking 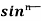 ¹x as first function and sinx as second function, integrate by parts,

Iⁿ = -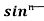¹x cosx – (n -1) 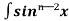cosx(-cosx)dx

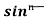= -¹x cosx  + (n - 1) 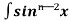cos²xdx

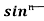= -¹x cosx  + (n - 1) 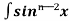( 1 - sin²x) dx

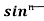= -¹x cosx  + (n - 1) 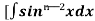- 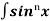dx

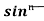=  -¹x cosx  + (n - 1) [ Iⁿ ‾ ² - Iⁿ]

By solving above

Iⁿ  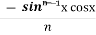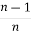=   + Iⁿ‾²

This is the reduction formula for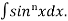

Example: Evaluate 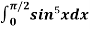by using reduction formula.

Solution:  we know that,

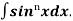
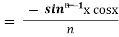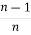     + Iⁿ‾²,     here   Iⁿ‾² =

Now using this formula,

=

=

=

=

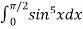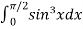
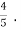
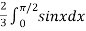
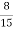
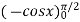
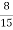
(b). Reduction formula for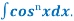     

Similarly we can get the formula for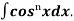       

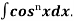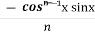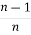  =    + Iⁿ‾²       

We can use the following formulas to get the result easily,

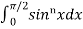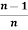  = . .    ,       only if n is odd and n ≥3

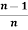= . . . ,       only if n is even and n ≥2

We apply same formula for cos x.

Example2: evaluate .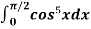

Solution: we will apply reduction formula to evaluate,

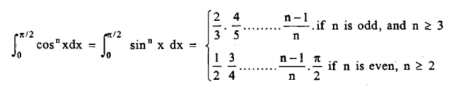
So, here n = 5, which is odd,   we will get ,

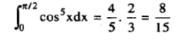
(C) Reduction formula for: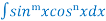

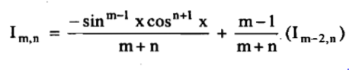
Where.

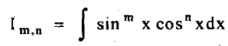
Example1: Evaluate 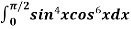by using reduction formula,

Solution:  here, m = 4, n = 6,

Now we will apply above reduction formula,

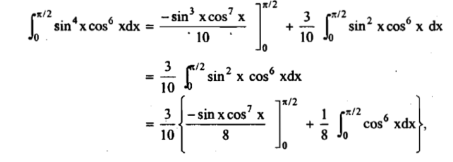
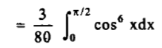
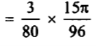
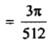
Example2: Evaluate 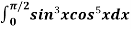by using reduction formula.

Solution:     Here we can see that, m = 3 and n = 5,

Now we will apply reduction formula,

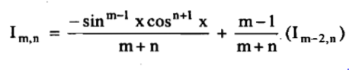
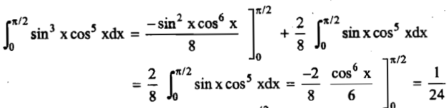
Curve tracing -  An introduction

A picture explains more clearly than words and numbers. A curve which is the image of functional relationship gives us a lot information about the relation. We can get information analyzing the equation itself but the associated curve is often easy and understandable.

Let’s study about how to trace the curves of various equations in different forms like Cartesian, parametric and polar.

Important definitions for curve tracing

Here are some terms that we use in curve tracing:

1. Double point- when a curve passes two times through this point is known as double point.

2. Node- a double point at which two real tangents can be drawn.(tangents should not be coincide)

3. Cusp -  a double point is a cusp when two tangents are coincide on it.

Tracing a curve- Cartesian form

Let us the equation of a curve is f(x,y)=0 , now we will learn few steps to simplify tracing of this curve.

1. The first step to find out the region of the plane. For example no point in the curve x= y² in second and third quadrant as we will always get a positive value on x-axis. That means our curve will lie on first and fourth quadrant only.

2. The second step is to find out If the curve is symmetrical about any line or origin.

Some examples of symmetrical curves are as below-

                                                                                                         Y

            Y

                                                       X                                                        O                                       X   

Symmetric about the x-axis                                                 Symmetric about origin

Steps to determine the symmetry of a curve:

1. If all the powers of x in function f(x,y)=0 are even, then f(x,y)= f(-x,y) and the curve is always symmetrical about y-axis. Similarly we can draw the conclusion about x-axis

2.If f(x,y)= 0 & f(-x,-y)= 0 , then the curve is symmetrical about the origin.

3. If the equation of the curve does not change when we interchange x and y then it is symmetrical about the line y= x

Let’s understand this with the help of following table-

4. The next step to determine the points where curve intersects the axes. If we put y = 0 in f(x,y)=0 and solve the equation, we get the points interecting on x-axis. Smilarly we get point on y- axis.

5. Now we try to locate the points for discontinuity of the function.

6. Calculate dy/dx to locate the portion where the curve is rising( dy/dx>0) or falling(dy/dx<0)

7. Calculate d²y/dx² to locate maxima and minima and the point of inflection

For maxima = dy/dx = 0,  d²y/dx²<0      &     for minima = dy/dx = 0,  d²y/dx²>0

For point of inflection -  d²y/dx² = 0

8. The next step is to find the asymptotes,

9. Another point to determine the singular point. The shape of the curve at these points generally more complex.

10. Finally plot the points as many as we can. Also try to draw tangents to the curve at some points(calculate the derivative). Now join the plotted point by a smooth curve.

Now we will understand curve tracing with some easy examples:

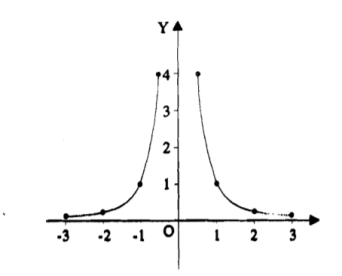
Example-:  Trace the curve y = 1/x².

Sol.          As we can see y- coordinates of the curve can not be negative. So the                                              curve must be above x-axis. The curve is also symmetric about y-axis so we can draw the graph only in single side.

Here, we will find the first and second derivatives-

So, dy/dx= -2/x³ and  d²y/dx² = 6/ x⁴    ,  here  dy/dx <0 for all x>0 so we can say that the function is non- increasing so the graph falls as we increase x.

Also second derivative is also non zero so there are no point of inflection.

Here the curve is x²y=1 (rewritten), here both the axes are asymptotes of the curve.

Here is the figure of the curve-:

Example-2: Trace the curve y= (x+2)²(x-1).

Sol. Here first we check the slant asymptotes (there is no vertical asymptote)

So, p =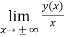

=

=

=

=  ) = +

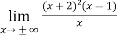
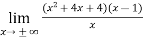
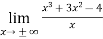
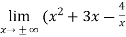Since p is infinity then the function has no slant asymptotes.

Now we will find the point of intersection with axes:

Y(0)= -4;

Put y(x)= 0,     (x+2)²(x-1)= 0

We get by solving,       X1= -2,     x2= 1

Now calculate the first derivative,

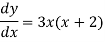
Here we will find stationary point by putting first derivative equal to zero:

3x(x+2) = 0

X1 = 0,   x2 = -2

X= -2 is maximum and x= 0 is minimum point.

The value of the function at these points will be:

Y= -4, 0

Now we will find second derivative:

Now, d²y/dx² = 6x+6,

So the function is strictly upward for:

X<-1,

And strictly downward for

x>-1,

Hence x= -1 is the inflection point

We get    y(-1)= -2

Here is the figure of curve:

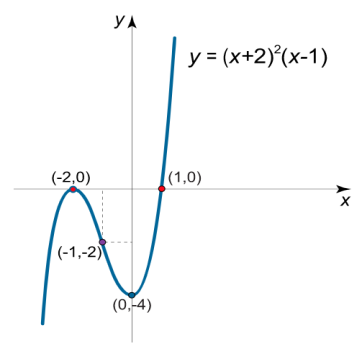
Tracing a curve- parametric form

Before we start tracing curves of the equations in parametric form, here first we understand the definition of parametric equations:

Parametric equations:

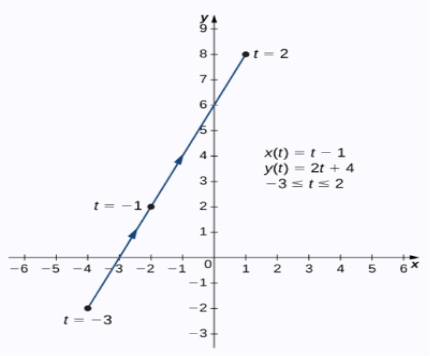
If x and y are the continuous functions of “t” on an interval I  , then the equations:

x = x(t)

And

y= y(t)

Are called parametric equations and t is called the parameter.

Now let’s understand how to trace the curves in parametric by examples:

Example1: trace the curve of the following parametric equations:

,     x(t) = t-1 ,     y(t) = 2t+4         -3<

Sol.  Here we will create the table for t, x(t) and y(t)  , t is independent variable in both case,

Here value of t lies between -3 to 2.

By plotting these set of point we get a curve as below.

Arrows in the graph indicates the orientation of the graph.

Tracing a curve- polar form

To trace the polar curve r = f (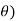 we follow the following steps:

1. Symmetry – (a) if the equation is an even function of 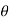, then the curve is symmetrical about the initial line.

(b)  if the equation is an even function of r, then the curve is symmetrical about the origin/

(C ). If the equation remains same if we change 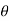by - 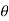and r by –r then the curve is symmetric about the line through the pole and perpendicular to the initial line.

2. Region- Find the reason for 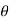for which r is defined and real

3. Table- make table for the values of r determined by .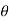

4. Angle 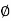-  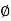 is the angle between the radius vector and tangent to the curve;

= )

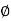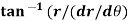Then angle 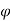= 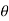+ 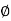, tangents to the curve can be determined by angle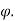

5. Asymptotes-   find the asymptotes of the curve.

Now we will understand of tracing of polar equations by an example:

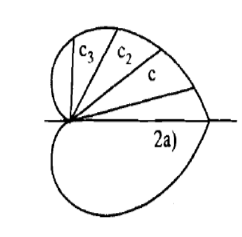
Example: Trace the curve r = a(1+ cos.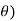

Sol.    Here we can see clearly cos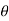 = cos(-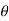), hence the curve is symmetric about initial line.

Since -1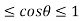, the curve lies inside the circle r = 2a

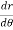= -asin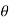 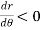    , when  0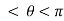, thus r decreases as 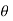increases in the interval 0 to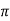 

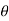	0
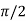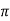r	2a	a	0

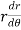= - cot (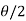) = tan( 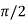 + 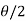),      this shows the angle between r and 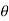and the tangent is 0 or  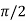   according to  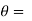 0 or 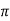. Hence the line joining a point on the curve to the origin is orthogonal to the tangent when  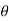 = 0 and coincides with