UNIT 2
PARTIAL DIFFERENTIATION 1
Let 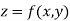
Then partial derivative of z with respect to x is obtained by differentiating z with respect to x treating y as constant and is denoted as

Then partial derivative of z with respect to y is obtained by differentiating z with respect to y treating x as constant and is denoted as
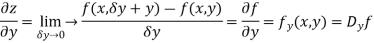
Partial derivative of higher order:
When we differentiate a function depend on more than one independent variable, we differentiate it with respect to one variable keeping other as constant.
A second order partial derivative means differentiating twice
In general 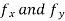 are also function of x and y and so these can be further partially differentiated with respect to x and y.
are also function of x and y and so these can be further partially differentiated with respect to x and y.
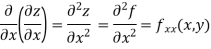
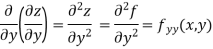
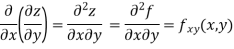
In general 
Notation:
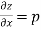
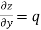

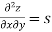
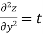
Generalization: If 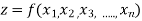
Then the partial derivative of z with respect to  is obtained by differentiating z with respect to
is obtained by differentiating z with respect to 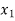 treating all the other variables as constant and is denoted by
treating all the other variables as constant and is denoted by
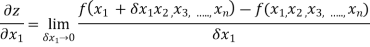
Example1:If 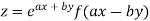 . Then prove that
. Then prove that
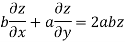
Given 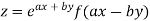
Partially differentiating z with respect to x keeping y as constant
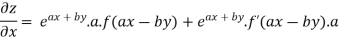
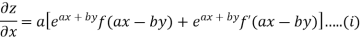
Again partially differentiating given z with respect to y keeping x as constant
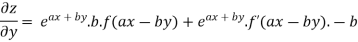
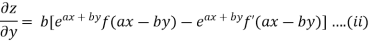
On b.eq(i) +a.eq(ii) we get
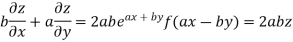
Hence proved.
Example2 : If 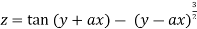
Show that 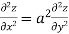
Given 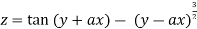
Partially differentiating z with respect to x keeping y as constant
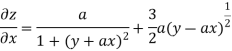
Again partially differentiating z with respect to x keeping y as constant
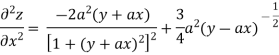
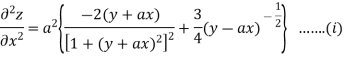
Partially differentiating z with respect to y keeping x as constant
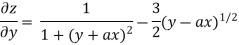
Again partially differentiating z with respect to y keeping x as constant
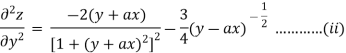
From eq(i) and eq(ii) we conclude that
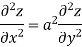
Example3 : Find the value of n so that the equation
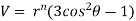
Satisfies the relation 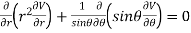
Given 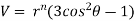
Partially differentiating V with respect to r keeping 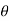 as constant
as constant
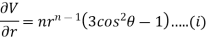
Again partially differentiating given V with respect to 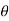 keeping r as constant
keeping r as constant
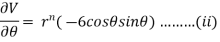
Now, we are taking the given relation
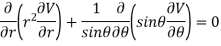
Substituting values using eq(i) and eq(ii)
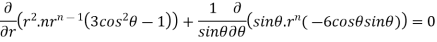
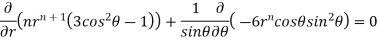
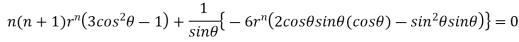
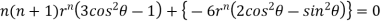
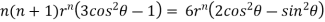
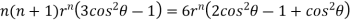
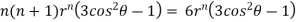
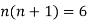
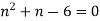
On solving we get 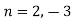
Example 4 : If 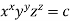 then show that when
then show that when 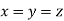
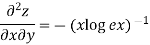
Given 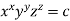
Taking log on both side we get

Partially differentiating with respect to x we get

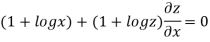
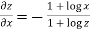 …..(i)
…..(i)
Similarly partially differentiating with respect y we get
 ……(ii)
……(ii)
LHS 
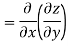
Substituting value from (ii)
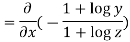
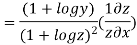
Again substituting value from (i) we get
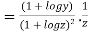 .(
.(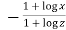 )
)
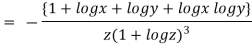
When 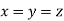
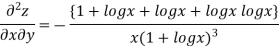
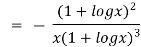
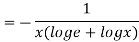
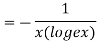
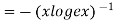
=RHS
Hence proved
Example5 :If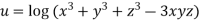
Then show that 
Given 
Partially differentiating u with respect to x keeping y and z as constant
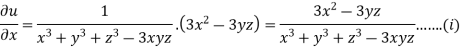
Similarly paritially differentiating u with respect to y keeping x and z as constant
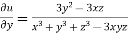 …….(ii)
…….(ii)
 ……..(iii)
……..(iii)
LHS: 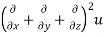
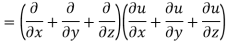
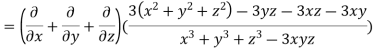
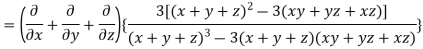
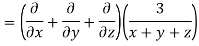
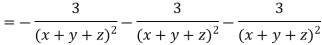

Hence proved
Homogenous Function: A function of the form
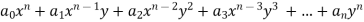
In this every term if of degree n, so it is called as homogenous function of degree n.
Rewriting the above as
= 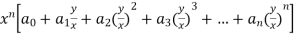
=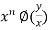
Thus every function which can be expressed as above form is called a homogenous function of degree n in x and y.
Generalization: A function 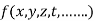 is an homogenous equation of degree n in
is an homogenous equation of degree n in 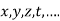 if it can be expressed as
if it can be expressed as 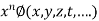
Euler’s Theorem:
If u be an homogenous function of degree n in x and y, then
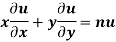
Proof: Given u is an homogenous function of degree n in x and y. So it can be rewrite as
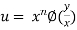 ……(i)
……(i)
Partially differentiating u with respect to x we get

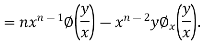
Again partially differentiating u with respect to y we get
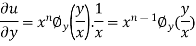
Therefore 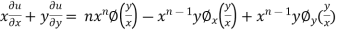
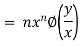
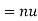
Thus 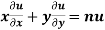
Hence proved
Corollary: If u is a homogenous function of degree n in x and y then

As we know that by Euler’s theorem
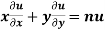 ……(i)
……(i)
Partially differentiating (i) with respect to x we get
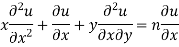
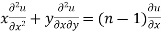 …..(ii)
…..(ii)
Partially differentiating (i) with respect to y we get
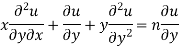
 …..(iii)
…..(iii)
Multiplying x by (ii) and y by (iii) then on adding we get
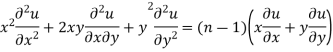
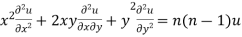 by using (i)
by using (i)
Thus 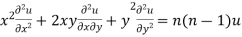
Note: We can directly use the Euler’s theorem and its corollary to solve the problems.
Example1 Show that 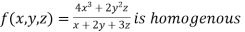
Given 
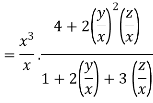
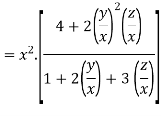
Therefore f(x,y,z) is an homogenous equation of degree 2 in x, y and z
Example2 If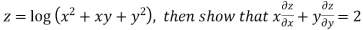
Let 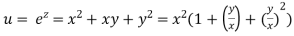
Thus u is an homogenous function of degree 2 in x and y
Therefore by Euler’s theorem
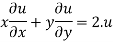
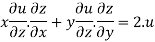
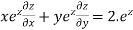 substituting the value of u
substituting the value of u
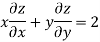
Hence proved
Example3If 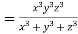 , find the value of
, find the value of 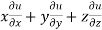
Given 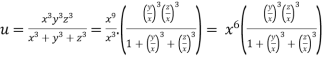
Thus u is an homogenous function of degree 6 in x ,y and z
Therefore by Euler’s theorem
Example4 If 
Given 
Thus u is an homogenous equation of degree -1 in x and y
Therefore by Euler’s theorem


Chain rule for two sets of independent variables
If u=u(x,y) and the two independent variables x,y are each a function of two new independent variables s,t then we want relations between their partial derivatives.
1.when u =u(x,y),


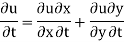
Conversely, when u= u(s,t).
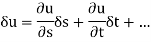
Then when s =s(x,y) and t =t(x,y).
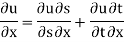

Example:1
Solve the following using chain Rule
Y=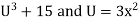
Solution:
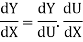
Then ,
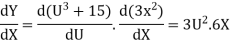
Substituting U =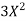 in the above we have
in the above we have
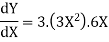
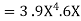
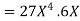

Example 2:
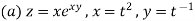
There really isn’t all that much to do here other than using the formula
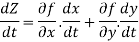
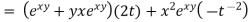
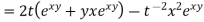
So, technically we’ve computed the derivative .However ,we should probably go ahead and substitute in for x and y as well doing this gives
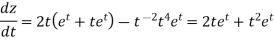
Right actually have been easier to just substitute in for x and y in the original function and just compute the derivative.
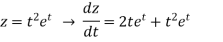
Reference Books:
1. A text book of Applied Mathematics Volume I and II by J.N. Wartikar and P.N. Wartikar
2. Higher Engineering Mathematics by Dr. B. S. Grewal
3. Advanced Engineering Mathematics by H. K. Dass
4. Advanced Engineering Mathematics by Erwins Kreyszig