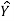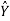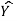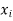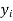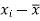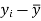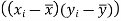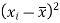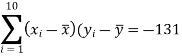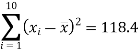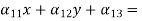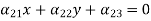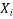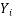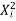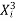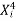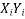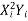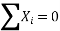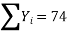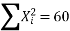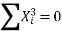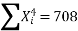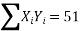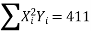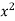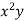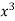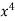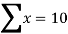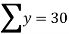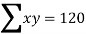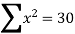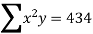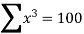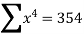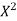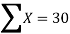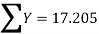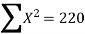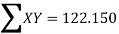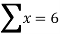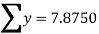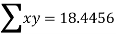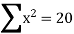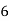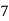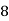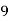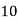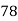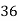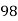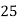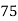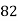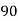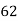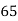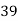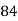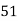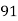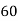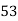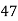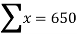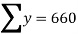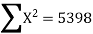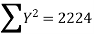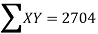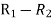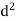UNIT 5
Statistics
Curve Fitting of Type y=axb Algorithm
In this article we are going to develop an algorithm for fitting curve of type
y = axb using least square regression method.
Procedure for fitting y = axb
We have,
y = axb ----- (1)
Taking log on both side of equation (1), we ge
log(y) = log(axb)
log(y) = log(a) + log(xb)
log(y) = log(a) + b*log(x) ----- (2)
Now let Y = log(y), A = log(a) and X = log(x)
then equation (2) becomes,
Y = A + bX ----- (3),
Now we fit equation (3) using least square regression as:
1. Form normal equations:
∑Y = nA+ b ∑X
∑XY = A∑X + b∑X2
2. Solve normal calculations as simultaneous equations for A and b
3. We calculate a from A using:
a = exp(A)
4. Substitute the value of a and b in
y= axb to find line of best fit.
Example 1:
Fit a least square line for the following data. Also find the trend values and show that ∑(Y–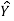 )=0 ∑(Y–
)=0 ∑(Y–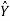 )=0.
)=0.
X | 1 | 2 | 3 | 4 | 5 |
Y | 2 | 5 | 3 | 8 | 7 |
Solution:
X | Y | XY | X2 |
| Y– |
1 | 2 | 2 | 1 | 2.4 | -0.4 |
2 | 5 | 10 | 4 | 3.7 | +1.3 |
3 | 3 | 9 | 9 | 5.0 | -2 |
4 | 8 | 32 | 16 | 6.3 | 1.7 |
5 | 7 | 35 | 25 | 7.6 | -0.6 |
∑X=15 | ∑Y=25 | ∑XY=88 | ∑X 2=55 | Trend Values | ∑(Y-
|
The equation of least square line Y=a +bX
Normal equation for ‘a’ ∑Y=na+b 25=5a+15b —- (1)
Normal equation for ‘b’ ∑XY = a∑X+b∑X2 88=15a+55b —-(2)
Eliminate a a from equation (1) and (2), multiply equation (2) by 3 and subtract from equation (2).
Eliminate a from equation (1) and (2), multiply equation (2) by (3) and subtract from equation (2). Thus we get the values of a and b
Here a=1.1 and b=1.3 , the equation of least square line becomes
Y=1.1+1.3X
example 2:
using least square method to fit a straight line of the following data
X | 8 | 2 | 11 | 6 | 5 | 4 | 12 | 9 | 6 | 1 |
y | 3 | 10 | 3 | 6 | 8 | 12 | 1 | 4 | 9 | 14 |
Solution:
First we calculate 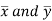 for the given data
for the given data
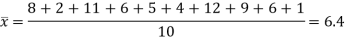
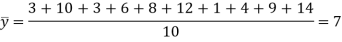
Now we calculate 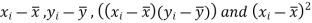
i |
|
|
|
|
|
|
1 | 8 | 3 | 1.6 | -4 | -6.4 | 2.56 |
2 | 2 | 10 | -4.4 | 3 | -13.2 | 19.36 |
3 | 11 | 3 | 4.6 | -4 | -18.4 | 21.16 |
4 | 6 | 6 | -0.4 | -1 | 0.4 | 0.16 |
5 | 5 | 8 | -1.4 | 1 | -1.4 | 1.96 |
6 | 4 | 12 | -2.4 | 5 | -12 | 5.76 |
7 | 12 | 1 | 5.6 | -6 | -33.6 | 31.36 |
8 | 9 | 4 | 2.6 | -3 | -7.8 | 6.76 |
9 | 6 | 9 | -0.4 | 2 | -0.8 | 0.16 |
10 | 1 | 14 | -5.4 | 7 | -37.8 | 29.16 |
|
|
|
|
|
|
|
Calculate the slope
m = 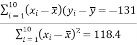 = -131/118.4
= -131/118.4 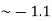
calculate the y-intercept
use the formula to calculate the y-intercept
b = 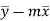
= 7-(-1.1*6.4)
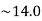
The required line equation is
Y= -1.1x+14.0
Second-order curve
A plane curve whose rectangular Cartesian coordinates fulfil an algebraic calculation of the second degree:
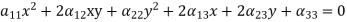
Equation need not define a real geometrical form, but to reserve generality in such situations one says that it describes an imaginary second-order curve. Depending on the values of the coefficients of the equation it can be changed by parallel movement and rotation of the coordinate system through some angle to one of the 9 canonical forms given under, to each of which there agrees a definite class of curves. Viz.,
non-degenerate curves:
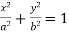 , ellipses (cf. Ellipse);
, ellipses (cf. Ellipse);
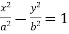 , hyperbolas (cf. Hyperbola);
, hyperbolas (cf. Hyperbola);
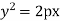 , parabolas (cf. Parabola);
, parabolas (cf. Parabola);
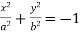 , imaginary ellipses;
, imaginary ellipses;
degenerate curves:
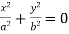 , pairs of imaginary intersecting lines;
, pairs of imaginary intersecting lines;
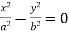 , pairs of real intersecting lines;
, pairs of real intersecting lines;
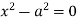 , pairs of real parallel lines;
, pairs of real parallel lines;
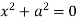 , pairs of imaginary parallel lines;
, pairs of imaginary parallel lines;
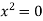 ,a pair of coincident real lines.
,a pair of coincident real lines.
A second-order curve that has a unique centre of symmetry (the centre of the second-order curve) is named a central curve. The coordinates of the centre of a second-order curve are determined by the explanation of the system
|
A second-order curve without a centre of symmetry or with an indefinite centre is named a non-central curve.
Example 1:
X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Y | 2 | 6 | 7 | 8 | 10 | 11 | 11 | 10 | 9 |
Solution:
X |
|
|
|
|
|
|
|
1 | -4 | 2 | 16 | -64 | 256 | -8 | 32 |
2 | -3 | 6 | 9 | -27 | 81 | -8 | 54 |
3 | -2 | 7 | 4 | -8 | 16 | -14 | 28 |
4 | -1 | 8 | 1 | -1 | 1 | -8 | 8 |
5 | 0 | 10 | 0 | 0 | 0 | 0 | 0 |
6 | 1 | 11 | 1 | 1 | 1 | 11 | 11 |
7 | 2 | 11 | 4 | 8 | 16 | 22 | 44 |
8 | 3 | 10 | 9 | 27 | 81 | 30 | 90 |
9 | 4 | 9 | 16 | 64 | 256 | 36 | 144 |
N=0 |
|
|
|
|
|
|
|
∑Y i =Na+b∑X i +c∑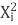
∑X i Y i =a∑X i +b∑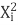 +c∑
+c∑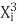
∑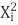 Y i =a∑
Y i =a∑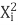 +b∑
+b∑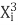 +c∑
+c∑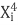
The required parabola is of the form y= ax2+bx+c
∴74=9a+b(0)+60c∴9a+60c=74…(i)
51=a(0)+60b+0c ∴60b=51 ∴b=5160 =0.85411=60a+0b+708 c∴60a+708c=411…(ii)
Solving (i) and (ii) simultaneously, we get
a=10.004 , c=-0.267
The Equation of parabola is therefore,
y=10.004+0.85X−0.267X 2
=10.004+0.85(x−5)−0.267(x−5) 2
=10.004+0.85x−4.25−0.267(x 2 −10x+25)
=10.004+0.85x−4.25−0.267x 2 +2.67x−6.675
∴ y = −0.921+3.52x−0.267x 2
Example 2:
Find the least square approximation of degree two to the data
X | 0 | 1 | 2 | 3 | 4 |
y | -4 | -1 | 4 | 11 | 20 |
Solution:
x | y | xy |
|
|
|
|
0 | -4 | 0 | 0 | 0 | 0 | 0 |
1 | -1 | -1 | 1 | -1 | 1 | 1 |
2 | 4 | 8 | 4 | 16 | 8 | 16 |
3 | 11 | 33 | 9 | 99 | 27 | 81 |
4 | 20 | 80 | 16 | 320 | 64 | 256 |
|
|
|
|
|
|
|
the normal equations are:
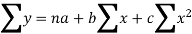
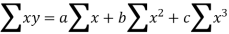
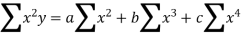
Here,
n = 5, 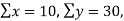
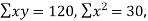
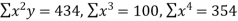
by substituting all the above values in normal equations we get,
30 = 5a+10b+30c
120=10a+30b+100c
434=30a+100b+354c
By solving the above equations we get
a = -4, b=2,c=1.
Therefore the required polynomial is
Y= -4x+2x+x2 and errors =0
Example 1:
Determine the constants a and b by the method of least square such that 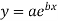
X | 2 | 4 | 6 | 8 | 10 |
y | 4.077 | 11.084 | 30.128 | 81.897 | 222.62
|
Solution:
The given relation is 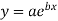
Taking logarithms on both sides we get,
log y = log a+ bx…..(1)
let,
log y = Y
x = X
log a = A
b = B
now we have,
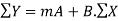 ….(2)
….(2)
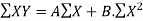 ….(3)
….(3)
Now we need to find 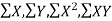
X=x | Y =ln(y) |
| xy |
2 | 1.405 | 4 | 2.810 |
4 | 2.405 | 16 | 9.620 |
6 | 3.405 | 36 | 20.430 |
8 | 4.405 | 44 | 35.240 |
10 | 5.405 | 100 | 54.050 |
|
|
|
|
The normal equations to fit the straight line is
Y = logey
Y= ln(y)
17.025 = 5A +30B…..(4) 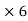
122.150 = 30A+220B….(5)
By solving 4 and 5 we get
30A +180B = 102.15…(4)
30A+220B = 122.150…(5)
We get a = 0.405 ,b = 0.5
A =log a 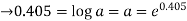
a = 1.499
since we have X=x and Y=y
log y=Y,
And we know y= aebx
Y = (1.499)e0.5x is the required exponential curve.
Example 2:
Fit the curve of the form y= aebx for the following data
X | 0 | 2 | 4 |
y | 8.12 | 10 | 31.82 |
Solution:
The given relation is 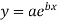
Taking logarithms on both sides we get,
log y = log a+ bx logee…..(1)
the required normal equations are,
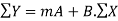 ….(2)
….(2)
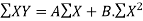 ….(3)
….(3)
We have n=3
x | y | Y= logey | xy | X2 |
0 | 8.12 | 2.0943 | 0 | 0 |
2 | 10 | 2.3026 | 4.6052 | 4 |
4 | 31.82 | 3.4601 | 13.8404 | 16 |
|
|
|
|
|
The normal equations become
3A +6b = 7.8750
6A + 20 b = 18.4456
By solving the above two equations we get
A = 1.361 and b = 0.3415
Since A =logea 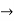 a = e1.361 = 6.9317
a = e1.361 = 6.9317
The curve of the fit is 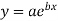
Thus,the required equation is,
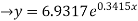
Whenever two variables x and y are so related that an increase in the one is accompanied by an increase or decrease in the other, then the variables are said to be correlated.
For example, the yield of crop varies with the amount of rainfall.
If an increase in one variable corresponds to an increase in the other, the correlation is said to be positive. If increase in one corresponds to the decrease in the other the correlation is said to be negative. If there is no relationship between the two variables, they are said to be independent.
Perfect Correlation: If two variables vary in such a way that their ratio is always constant, then the correlation is said to be perfect.
KARL PEARSON’S COEFFICIENT OF CORRELATION:
rbetween two variables x and y is defined by the relation
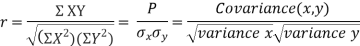
Where,X = x –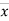 , Y = y –
, Y = y –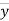
i.e. X, Y are the deviations measured from their respective means,
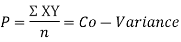
Example:Ten students got the following percentage of marks in Economics and Statistics
Calculate the 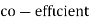 of correlation.
of correlation.
Roll No. |
|
|
|
|
|
|
|
|
|
|
Marks in Economics |
|
|
|
|
|
|
|
|
|
|
Marks in |
|
|
|
|
|
|
|
|
|
|
Solution:. Let the marks of two subjects be denoted by 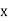 and
and 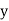 respectively.
respectively.
Then the mean for 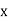 marks
marks 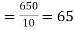 and the mean ofy marks
and the mean ofy marks 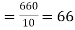
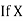 and
and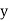 are deviations ofx’s and
are deviations ofx’s and 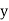 ’s from their respective means, then the data may be arranged in the following form:
’s from their respective means, then the data may be arranged in the following form:
x | y | X=x-65 | Y=y-66 | X2 | Y2 | XY |
78 36 98 25 75 82 90 62 65 39 | 84 51 91 60 68 62 86 58 53 47 | 13 -29 33 -40 10 17 25 -3 0 -26 | 18 -15 25 -6 2 -4 20 -8 -13 -19 | 169 841 1089 1600 100 289 625 9 0 676 | 324 225 625 36 4 16 400 64 169 361 | 234 435 825 240 20 -68 500 24 0 494
|
|
|
|
|
|
|
|
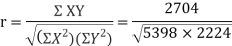
If the scatter diagram indicates some relationship between two variables 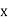 and
and 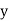 , then the dots of the scatter diagram will be concentrated round a curve. This curve is called the curve ofregression. Regression analysis is the method used for estimating the unknown values of one variable corresponding to the known value of another variable.
, then the dots of the scatter diagram will be concentrated round a curve. This curve is called the curve ofregression. Regression analysis is the method used for estimating the unknown values of one variable corresponding to the known value of another variable.
LINE OF REGRSSION
When the curve is a straight line, it is called a line of regression. A line of regression is the straight line which gives the best fit in the least square sense to the given frequency.
Example:Find the correlation 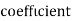 betweenx and
betweenx and 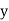 , when the lines ofregression are:
, when the lines ofregression are: 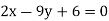 and
and 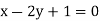
Solution. Let the line of regression ofx on 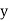 be
be 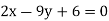
Then, the line ofregressionofy on 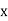 is
is 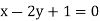
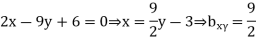
and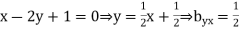
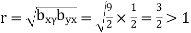 which is not possible. So our choice of regression line is incorrect.
which is not possible. So our choice of regression line is incorrect.
The regression line ofx on 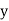 is
is 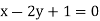
And, the regression line ofy on 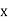 is
is 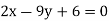
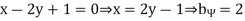
And 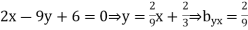
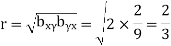
Hence the correlation coefficient between 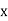 and
and 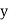 is
is 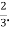
Example: The following regression equations were obtainedfrom a correlation table:
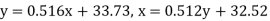
Find the value of 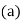 the correlation coefficient,
the correlation coefficient,
(b) the mean 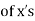 and
and
(c) the mean of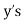
Solution.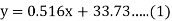
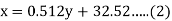
(a) From (1), 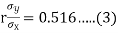
(b) From (2), 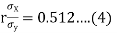
From (3) and (4)
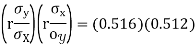
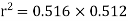
Coefficient of correlation 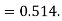
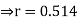
(b) (1) and (2) pass through the point 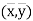 .
.
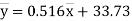 (5)
(5)
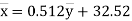 (6)
(6)
On solving (5) and (6), we get
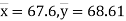
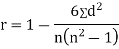
Solution. Let  be the ranks of
be the ranks of  individuals corresponding to two characteristics.
individuals corresponding to two characteristics.
Assuming nor two individuals are equal in either classification, each individual takes the values 1, 2, 3, 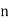 and hence their arithmetic means are, each
and hence their arithmetic means are, each
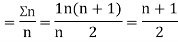
Let 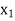 ,
, 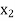 ,
, 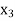 ,
, 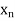 be the values of variable
be the values of variable 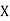 and
and 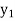 ,
, 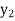 ,
, 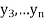 those of
those of 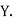
Then 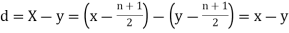
where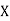 and y are deviations from the mean.
and y are deviations from the mean.
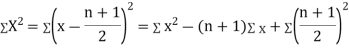
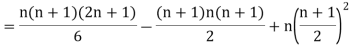
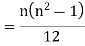
Clearly, 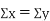 and
and 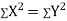
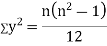
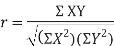
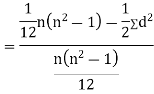
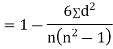
SPEARMAN’S RANK CORRELATION COEFFICIENT:
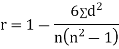
where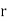 denotes rank coefficient of correlation and
denotes rank coefficient of correlation and 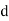 refers to the difference ofranks between paired items in two series.
refers to the difference ofranks between paired items in two series.
Example:Compute Spearman’s rank correlation coefficient r for the following data:
Person | A | B | C | D | E | F | G | H | I | J |
Rank Statistics | 9 | 10 | 6 | 5 | 7 | 2 | 4 | 8 | 1 | 3 |
Rank in income | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Solution:
Person | Rank Statistics | Rank in income | d= |
|
A | 9 | 1 | 8 | 64 |
B | 10 | 2 | 8 | 64 |
C | 6 | 3 | 3 | 9 |
D | 5 | 4 | 1 | 1 |
E | 7 | 5 | 2 | 4 |
F | 2 | 6 | -4 | 16 |
G | 4 | 7 | -3 | 9 |
H | 8 | 8 | 0 | 0 |
I | 1 | 9 | -8 | 64 |
J | 3 | 10 | -7 | 49 |
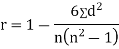
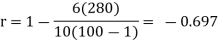
Example:IfXand Yare uncorrelated random variables, 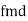 the
the 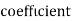 of correlation between
of correlation between 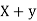 and
and 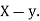
Solution.
Let 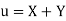 and
and 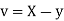
Then 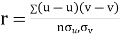
Now 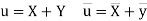
Similarly 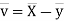
Now 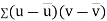
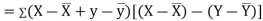
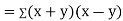
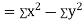
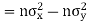
Also 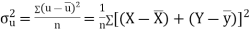
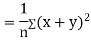
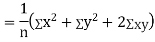
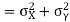 (As
(As 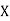 and
and 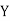 are not correlated, we have
are not correlated, we have 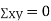 )
)
Similarly 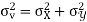
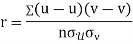
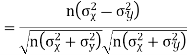
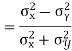
Reference Books:
1. A text book of Applied Mathematics Volume I and II by J.N. Wartikar and P.N. Wartikar
2. Higher Engineering Mathematics by Dr. B. S. Grewal
3. Advanced Engineering Mathematics by H. K. Dass
4. Advanced Engineering Mathematics by Erwins Kreyszig