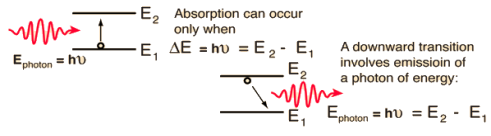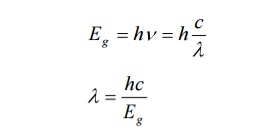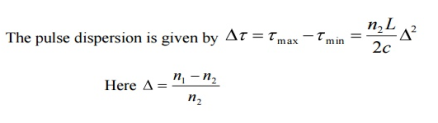UNIT-5
LASERS AND FIBRE OPTICS
Introduction
LASER stands for “Light Amplification by Stimulated Emission of Radiation”.
L = Light
A = Amplification (by)
S = Stimulated
E = Emission (of)
R = Radiation
The principle of laser amplification is stimulated emission.
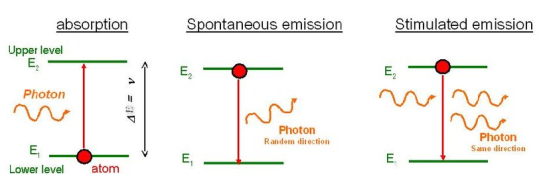
Let us discuss Einstein’s theory of the interaction of electromagnetic radiation with matter. He proposed that electromagnetic radiation interacts with matter in the following three steps.
- Stimulated Absorption
- Spontaneous Emission
- Stimulated Emission
Stimulated Absorption:
Let E1 and E2 be the energies of the ground and excited states of an atom. Suppose, if a photon of energy hν= E1− E2 interacts with an atom present in the ground state, the atom gets excitation from ground state E1 to excited state E2. This process is called stimulated absorption. Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons.
Stimulated absorption rate ∝ Number of atoms in the ground state
∝ The density of photons Spontaneous emission
|
Figure 1: Interaction of Radiation with Matter
Spontaneous Emission:
Let E1 and E2 be the energies of the ground and excited states of an atom. Suppose, if a photon of energy hν= E1− E2 interacts with an atom present in the ground state, the atom gets excitation from ground stateE1 to excited state E2. The excited atom does not stay a long time in the excited state. The excited atom gets de-excitation after its lifetime by emitting a photon of energy hν= E1− E2. This process is called spontaneous emission. Also Spontaneous means by its own. Here excited atom comes to the ground state on its own so it is named as spontaneous emission.
The spontaneous emission rate depends upon the number of atoms present in the excited state.
Spontaneous emission ∝ rate number of atoms in the excited state
Stimulated Emission:
This phenomenon is responsible for producing laser light. Let E1and E2 be the energies of the ground and excited states of an atom. Suppose, if a photon of energy hν= E1− E2 interacts with an atom present in the ground state, the atom gets excitation from ground stateE1 to excited state E2. Let, a photon of energy hν= E1− E2 interacts with the excited atom within their lifetime; the atom gets de-excitation to the ground state by emitting another photon. These photons have the same phase and it follows coherence. This phenomenon is called stimulated emission.
Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons.
Stimulated emission rate ∝ number of atoms in the excited state
∝ Density of photons
EINSTEIN’S COEFFICIENTS
The distribution of atoms in the two energy levels will change by absorption or emission of radiation. Einstein introduced three empirical coefficients to quantify the change of population of the two levels. Let N1 be the number of atoms per unit volume with energy E1 and N2 be the number of atoms per unit volume with energy E2. Let ‘n’ be the number of photons per unit volume at frequency ‘υ’ such that hυ= E1− E2.
Then, the energy density of photons ρ(υ) = nhυ
|
Figure 2: Interaction of photons with atoms
When these photons interact with atoms, both upward (absorption) and downward (emission) transition occurs.
At the equilibrium, the upward transitions must be equal to downward transitions.
Upward Transition
Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons.
We have seen above that
Stimulated absorption rate ∝ N1 i.e. Number of atoms in the ground state
∝ ρ(υ) i.e. Density of photons spontaneous emission
Stimulated absorption rate = B12N1ρ(υ) ……… (1)
Where B12 is the Einstein coefficient of stimulated absorption.
Downward transition
The spontaneous emission rate depends upon the number of atoms present in the excited state.
Spontaneous emission rate ∝ N2 i.e. number of atoms in the excited state
Spontaneous emission rate = A21N2 ……… (2)
Where A21 is the Einstein coefficient of spontaneous emission.
Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons.
Stimulated emission rate ∝ N2 i.e. number of atoms in the excited state
∝ ρ(υ) i.e. Density of photons
Stimulated emission rate = B21N2ρ(υ) ……… (3)
If the system is in equilibrium the upward transitions must be equal to downward transitions.
upward transitions = downward transitions
B12N1ρ(υ) = A21N2 + B21N2ρ(υ) ……… (4)
B12N1ρ(υ) - B21N2ρ(υ) = A21N2
(B12N1- B21N2) ρ(υ) = A21N2
ρ(υ) =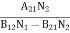
………(5)
Divide with B21N2 in numerator and denominator in the right side of the above equation,
ρ(υ) =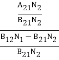 
= 
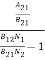………(6)
ρ(υ) =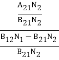 
= 
=
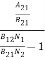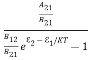………(7)
We know from Maxwell Boltzmann distribution law
= 
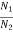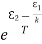……… (8)
And also from Planck’s law, the radiation density
ρ(υ) =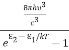 
………(9)
Comparing the two equations (7) and (9)
=
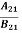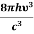and 
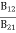=1 ……… (10)
The above relations are referred to as Einstein relations.
From the above equation for non-degenerate energy levels, the stimulated emission rate is equal to the stimulated absorption rate at the equilibrium condition.
= 
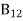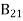………(11)
Key Takeaways
LASER stands for “Light Amplification by Stimulated Emission of Radiation”.
Einstein gave his theory of the interaction of electromagnetic radiation with matter. He proposed that electromagnetic radiation interacts with matter in the following three steps. Stimulated Absorption, Spontaneous Emission and Stimulated Emission
Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons.
The spontaneous emission rate depends upon the number of atoms present in the excited state.
Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons.
The Einstein relations is given as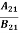 
=
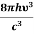and 
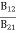=1
The laser light exhibits some peculiar properties compare with the conventional light. Those are
1. Highly monochromatic
2. Highly coherence
3. Highly directionality
4. Highly intense
5. Laser Speckles
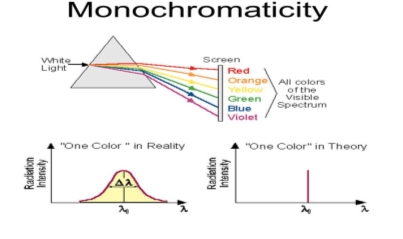
1. Highly monochromatic
Monochromatic light means a light containing a single colour or wavelength. The photons emitted from ordinary light sources have different energies, frequencies, wavelengths, or colours. Ordinary light is a mixture of waves having different frequencies or wavelengths. The light waves of laser have a single wavelength or colour.
|
Figure 3: Monochromatic
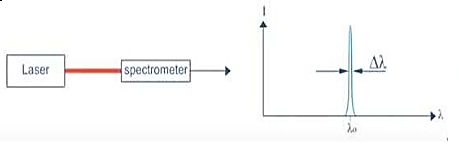
Therefore, laser light covers a very narrow range of frequencies or wavelengths.
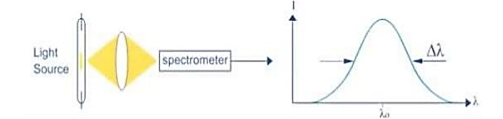
Hence The laser light is more monochromatic than that of a conventional light source. This may be due to the stimulated characteristic of laser light. The bandwidth of the conventional monochromatic light source is 1000 Å. But the bandwidth of an ordinary light source is 10 Å. For high sensitive laser source is 10-8 Å.
|
Figure 4: Intensity- wavelength graph for light and laser
2. Highly coherence
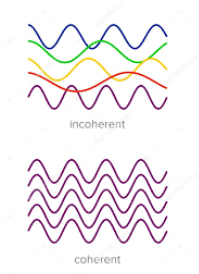
Definition: - A predictable correlation of the amplitude and phase at any one point with another point is called coherence.
|
Figure 5: Incoherence and coherence
Two waves are said to be coherent, the waves must have
In the case of conventional light, the property of coherence exhibits between a source and its virtual source whereas in the case of laser the property coherence exists between any two or more light waves.
There are two types of coherence
- Temporal coherence
- Spatial coherence
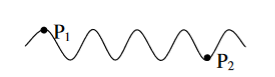
Temporal coherence (or longitudinal coherence): -
The predictable correlation of amplitude and phase at one point on the wave train w. r. at another point on the same wave train, then the wave is said to be temporal coherence
To understand this, let us consider two points P1 and P2 on the same wave train, which is continuous as shown in the figure.
|
Figure 6: Wave train
Suppose the phase and amplitude at any one point is known, then we can easily calculate the amplitude and phase for any other point on the same wave train by using the wave equation
y= a sin (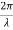
(ct-x))
Where ‘a’ is the amplitude of the wave and ‘x’ is the displacement of the wave at any instant of time ‘t’.
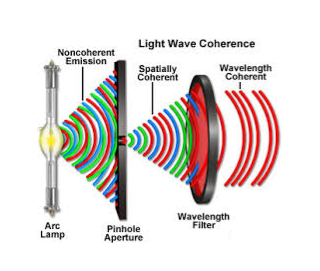
Spatial coherence (or transverse coherence) The predictable correlation of amplitude and phase at one point on the wave train w. r. t another point on a second wave, then the waves are said to be spatial coherence (or transverse coherence)
|
Figure 7: Spatial coherence
3. Highly directionality
The light ray coming from an ordinary light source travels in all directions, but laser light travels in a single direction. For example, the light emitted from torchlight spreads 1km distance it spreads 1 km distance. But the laser light spreads a few centimetres distance even it travels lacks kilometre distance.
The directionality of the laser beam is expressed in terms of divergence
∆θ =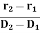
Where r1 and r2 are the radii of laser beam spots at distances of D1 and D2 respectively from the laser source.
4. Highly Intense or Brightness
We know that the intensity of a wave is the energy per unit time flowing through a unit's normal area. Laser light is highly intense than conventional light. A one mill watt He-Ne laser is highly intense than the sun intensity. This is because of the coherence and directionality of the laser. Suppose when two photons each of amplitude a are in phase with other, then young’s principle of superposition, the resultant amplitude of two photons is 2a and the intensity is 4a2. Since in laser many numbers of photons are in phase with each other, the amplitude of the resulting wave becomes na and hence the intensity of the laser is proportional to n2a2. So 1mW He-Ne laser is highly intense than the sun.
In an ordinary light source, the light spreads out uniformly in all directions. If you look at a 100 Watt lamp filament from a distance of 30 cm, the power entering your eye is less than 1/1000 of a watt. If you look at laser beam X (caution: don’t do it at home, direct laser light can damage your eyes) X, then all the power in the laser would enter your eye. Thus, even a 1 Watt laser would appear many thousand times more intense than a 100 Watt ordinary lamp.
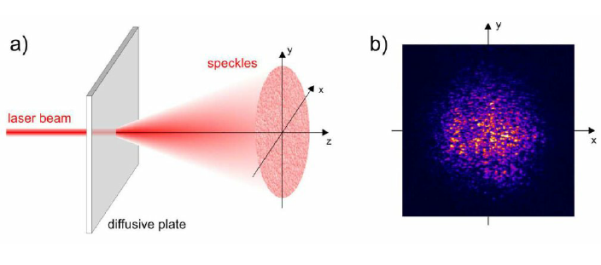
5. Laser Speckles
The term speckle refers to a random granular pattern that can be observed when a highly coherent light beam is diffusely reflected at a surface with a complicated structure. This phenomenon results from the interference of different reflected portions of the incident beam with random relative optical phases.
|
Figure 8: Laser Speckles
Even minor changes of the conditions, such as of the illuminated spot or the direction of the incident laser beam, can change the detailed shape of a speckle pattern.
When laser light that has been scattered off a rough surface falls on another surface, it forms an "objective speckle pattern". If a photographic plate or another 2-D optical sensor is located within the scattered light field without a lens, a speckle pattern is obtained whose characteristics depend on the geometry of the system and the wavelength of the laser.
Key Takeaways
The laser light exhibits some peculiar properties compare with the conventional light. Laser light is highly monochromatic, coherence, directionality, intense and Laser Speckles.
A predictable correlation of the amplitude and phase at any one point with another point is called coherence.
There are two types of coherence: Temporal coherence and Spatial coherence.
The directionality of the laser beam is expressed in terms of divergence
∆θ =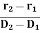
The intensity of a wave is the energy per unit time flowing through a unit's normal area.
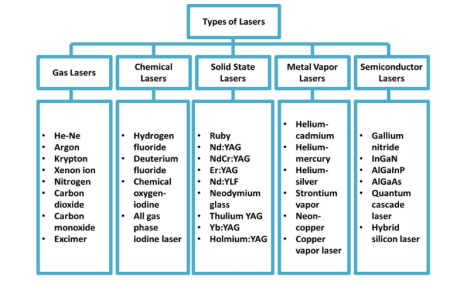
5.3.1 TYPES OF LASERS
Lasers are classified into 5 types based on the type of laser medium used:
Gas Laser
Chemical Laser
Solid-State Laser
Metal-Liquid Laser
Semiconductor Laser
|
Figure 9: Types of Laser
We will discuss three type of laser to give you a better idea how it works.
SOLID-STATE LASERS (RUBY LASER)
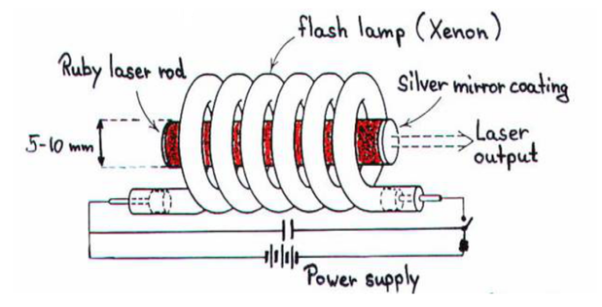
Ruby laser is a three-level solid-state laser and was constructed by Maiman in 1960. Ruby laser is one of the few solid-state lasers that produce visible light. It emits deep red light of wavelength 694.3 nm.
Construction
A ruby laser consists of three important elements: laser medium, the pump source, and the optical resonator.
Laser Medium
Ruby (Al2O3+Cr2O3) is a crystal of Aluminium oxide, in which 0.05% of Al+3 ions are replaced by the Cr+3 ions. The colour of the rod is pink. The active medium or laser medium in the ruby rod is Cr+3 ions. In ruby laser, 4cm length and 5mm diameter rod is generally used. The ruby has good thermal properties.
|
Figure 10: Ruby laser
The pump source
We know that population inversion is required to achieve laser emission. Population inversion is the process of achieving a greater population of a higher energy state than the lower energy state. To achieve population inversion, we need to supply energy to the laser medium i.e. to ruby crystal.
Xenon flash tube emits thousands of joules of energy in few milliseconds, but only a part of that energy is utilized by the chromium ions while the rest energy heats the apparatus. A cooling arrangement is provided to keep the experimental set up at normal temperatures.
Optical resonator
Working of ruby laser:
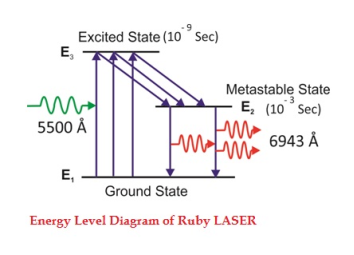
Consider a ruby laser medium consisting of three energy levels E1, E2, E3 with N number of electrons.
We assume that the energy levels will be E1 < E2 < E3. The energy level E1 is known as the ground state or lower energy state, the energy level E2 is known as the metastable state, and the energy level E3 is known as the pump state.
Let us assume that initially most of the electrons are in the lower energy state (E1) and only a tiny number of electrons are in the excited states (E2 and E3).
The energy level diagram of chromium ions is shown in the figure. The chromium ions get excitation into higher energy levels by absorbing 5500Å of wavelength radiation. The excited chromium ions stay in the level E3 for a short interval of time (10-8 to 10-9 Sec). After their life, most of the chromium ions are de-excited from E3 to E1 and a few chromium ions are de-excited from E3 to E2.
|
Figure 11: Energy Level diagram of ruby laser
Due to the continuous working of the flash lamp, the chromium ions are excited to a higher state E3 and returned to the E2 level. After a few milliseconds, the level E2 is more populated than the level E1 and hence the desired population inversion is achieved. The state of population inversion is not a stable one. The process of spontaneous transition is very high. When the excited chromium ion passes spontaneously from E3 to E2it emits one photon of wavelength 6943 Å. The photon reflects back and forth by the silver ends and until it stimulates an excited chromium ion in the E2 state and it to emit a fresh photon in phase with the earlier photon. The process is repeated again and again until the laser beam intensity is reached a sufficient value. When the photon beam becomes sufficiently intense, it emerges through the partially silvered end of the rod. The wavelength 6943 Å is in the red region of the visible spectrum.
The laser requires high pumping power
The efficiency of a ruby laser is very small
It is a pulse laser
Application of ruby laser
Ruby lasers are in optical photography
Ruby lasers can be used for the measurement of plasma properties such as electron density and temperature.
Ruby lasers are used to remove the melanin from the skin.
Ruby laser can be used for the recording of holograms.
Key Takeaways
Ruby laser is a three-level solid-state laser.
A ruby laser consists of three important elements: laser medium, the pump source, and the optical resonator.
Ruby laser is one of the few solid-state lasers that produce visible light. It emits deep red light of wavelength 694.3 nm.
HELIUM - NEON GAS LASER
Ruby laser is a pulse laser, even it has high intense output. For continuous laser beams, gas lasers are used. Using gas lasers, we can achieve high coherence, high directionality, and high monochromaticity beam. The output power of the gas laser is generally in few milliwatts.
- The helium-neon laser consists of three essential components:
- Pump source (high voltage power supply)
- Gain medium (laser glass tube or discharge glass tube)
- Resonating cavity
Pump source
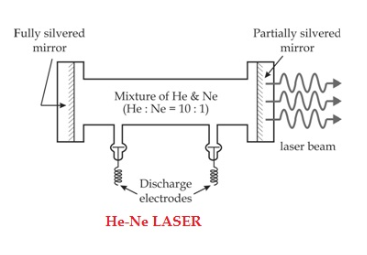
The gain medium of a helium-neon laser is made up of a mixture of helium and neon gas contained in a glass tube at low pressure. In the He-Ne gas laser, the He and Ne gases are taken in the ratio 10:1 in the discharge tube.
Gain medium
In He-Ne laser 80cm length and 1cm diameter discharge are generally used. The out power of these lasers depends on the length of the discharge tube and the pressure of the gas mixture. Therefore, to achieve population inversion, we need to pump electrons from the lower energy state of the helium. In He-Ne laser, neon atoms are the active centres and have energy levels suitable for laser transitions while helium atoms help in exciting neon atoms.
|
Figure 12: He-Ne Laser
Two reflecting mirrors are fixed on either end of the discharge tube, in that, one is partially reflecting and the other is fully reflecting. The fully silvered mirror will completely reflect the light whereas the partially silvered mirror will reflect most of the light but allows some part of the light to produce the laser beam.
WORKING
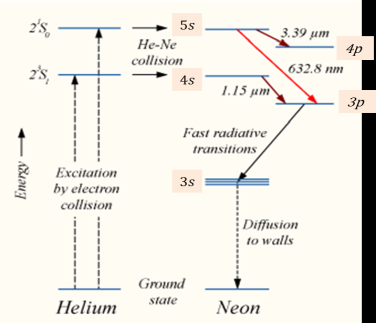
When the electric discharge is passing through the gas mixture, the electrons accelerated towards the positive electrode. During their passage, they collide with He atoms and excite them into higher levels. 23s1 and 21s0 form the ground state of the He atom. In higher levels, 23s1 and 21s0, the lifetime of The atoms is more. So there is a maximum possibility of energy transfer between He and Ne atoms through atomic collisions. When He atoms present in the levels 23s1 and 21s0 collide with the Ne atom's present ground state, the Ne atoms get excitation into higher levels 4s and 5s.
Due to the continuous excitation of Ne atoms, we can achieve the population inversion between the higher levels 4s and 5s and lower levels 3p and 4p. The various transitions 5s to 4p, 4s to 3p, and 5s to 3p leads to the emission of wavelengths 3.93μm, 1.51μm, and 6328 Å or 632.8μm.
|
Figure 13: Energy Level diagram of He-Ne Laser
ADVANTAGES OF HELIUM-NEON LASER
- The helium-neon laser emits laser light in the visible portion of the spectrum.
- High stability
- Low cost
- Operates without damage at higher temperatures
DISADVANTAGES OF HELIUM-NEON LASER
- Low efficiency
- Low gain
- Helium-neon lasers are limited to low power tasks
APPLICATIONS OF HELIUM-NEON LASERS
- Helium-neon lasers are used in industries.
- Helium-neon lasers are used in scientific instruments.
- Helium-neon lasers are used in the college laboratories
Key Takeaways
Helium-Neon laser is a type of gas laser in which a mixture of helium and neon gas is used as a gain medium.
The helium-neon laser was the first continuous-wave laser ever constructed.
The helium-neon laser consists of three essential components Pump source (high voltage power supply), Gain medium (laser glass tube or discharge glass tube), Resonating cavity
The helium-neon laser operates at a wavelength of 632.8 nanometres (nm), in the red portion of the visible spectrum.
SEMICONDUCTOR LASER
Semiconductor Laser
Semiconductor lasers represent one of the most important classes of lasers in use today, not only because of the large variety of direct applications in which they are involved but also because they have found widespread use as pumps for solid-state lasers.
Semiconductor lasers require, for the active medium, a direct gap material, and accordingly, the normal elemental semiconductors like Si or Ge cannot be used. The majority of semiconductor-laser materials are based on a combination of elements belonging to the third group of the periodic table such as Al, Ga, in with elements of the fifth group such as N, P, As, Sb. Examples include the best known GaAs as well as some ternary AlGaAs, InGaAs, and quaternary InGaAsP alloys.
InGaN semiconductor lasers the best candidates for semiconductor laser emission in the very important blue-green spectral region. Semiconductor laser materials are not limited to III–V compounds, however. For the blue-green end of the spectrum, we note that wide-gap semiconductors are using a combination between elements of the second group (such as Cd and Zn) and the sixth group (S, Se).
PRINCIPLE
When a p-n junction diode is forward biased, the electrons from the n – region and the holes from the p- region cross the junction and recombine with each other.
During the recombination process, the light radiation (photons) is released from a certain specified direct bandgap semiconductor like Ga-As. This light radiation is known as recombination radiation.
The photon emitted during recombination stimulates other electrons and holes to recombine. As a result, stimulated emission takes place which produces laser.
|
Figure 14: Semiconductor Laser
CONSTRUCTION
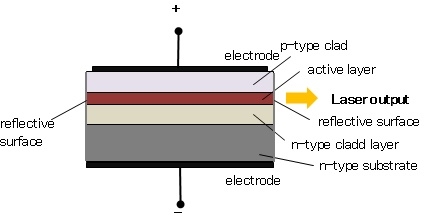
This light is not a laser yet; it is confined within the active layer because the refractive index of the clad layers is lower than that of the active layer. Besides both ends of the active layer act as a reflecting mirror where the light reciprocates in the active layer. Then, the light is amplified by the stimulated emission process and laser oscillation is generated.
The photon emission is stimulated in a very thin layer of PN junction (in order of few microns). The electrical voltage is applied to the crystal through the electrode fixed on the upper surface. The end faces of the junction diode are well polished and parallel to each other. They act as an optical resonator through which the emitted light comes out.
|
Figure 15: Construction of semiconductor Laser
WORKING
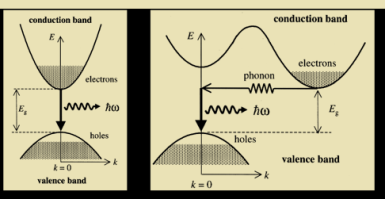
The region around the junction contains a large number of electrons in the conduction band and a large number of holes in the valence band.
If the population density is high, a condition of population inversion is achieved. The electrons and holes recombine with each other and this recombination produces radiation in the form of light.
When the forward-biased voltage is increased, more and more light photons are emitted and the light production instantly becomes stronger. These photons will trigger a chain of stimulated recombination resulting in the release of photons in phase.
|
Figure 16: Energy Level diagram of Semiconductor Laser
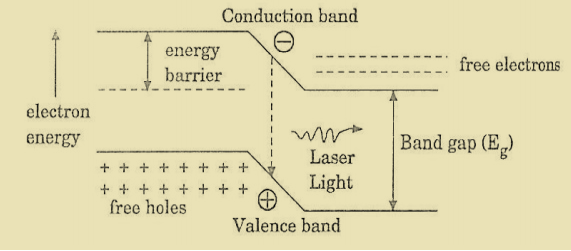
After gaining enough strength, it gives out the laser beam of wavelength 8400Å. The nature of output is a continuous wave or pulsed output. The power output from this laser is 1mW. The wavelength of laser light is given by
|
Where Eg is the bandgap energy in joule.
ADVANTAGES
It is very small in dimension.
The arrangement is simple and compact.
- It exhibits high efficiency.
- It is operated with lesser power than a ruby and CO2 laser.
- The laser output can be easily increased by controlling the junction current
- It requires very little auxiliary equipment
- It can have a continuous wave output or pulsed output.
DISADVANTAGES
- It is difficult to control the mode pattern and mode structure of the laser.
- The output is usually from 5 degrees to 15 degrees i.e., the laser beam has a large divergence.
- The purity and monochromaticity are power than other types of laser
- Threshold current density is very large (400A/mm2).
- It has poor coherence and poor stability.
APPLICATION
- It is widely used in fibre optic communication
- It is used to heal the wounds by infrared radiation
- It is also used as a pain killer
- It is used in laser printers and CD writing and reading.
Key Takeaways
It is a solid-state semiconductor laser. It is a specifically fabricated p-n junction diode.
Semiconductor laser is based on the principle that when a p-n junction diode is forward biased, the electrons from the n – region and the holes from the p- region cross the junction and recombine with each other.
During the recombination process, the light radiation (photons) is released from a certain specified direct bandgap semiconductor like Ga-As. This light radiation is known as recombination radiation.
The photon emitted during recombination stimulates other electrons and holes to recombine. As a result, stimulated emission takes place which produces laser.
A semiconductor laser is a device that causes laser oscillation by flowing an electric current to the semiconductor.
Semiconductor lasers require, for the active medium, a direct gap material, and accordingly, the normal elemental semiconductors like Si or Ge cannot be used.
5.3.2 APPLICATIONS OF LASER
Applications of lasers because of unique property of laser beam such as coherence, monochromacity, directionality, and high intensity, they are widely used in various fields like
1. Communication
2. Computers
3. Chemistry
4. Photography
5. Industry
6. Medicine
7. Military
8. Scientific Research
1. Communication
In case of optical communication semiconductors laser diodes are used as optical sources and its band width is (1014Hz) is very high compared to the radio and microwave communications. More channels can be sent simultaneously Signal cannot be tapped as the band width is large, more data can be sent. A laser is highly directional and less divergence, hence it has greater potential use in space crafts and submarine. It is used in optical fiber communications to send information over large distances with low loss. Laser light is used in underwater communication networks. Lasers are used in space communication, radars and satellites.
2. Computers
In LAN (local area network), data can be transferred from memory storage of one computer to other computer using laser for short time. Lasers are used in CD-ROMS during recording and reading the data. Lasers are used in computer printers.
3. Chemistry
Lasers are used in molecular structure identification Lasers are also used to accelerate some chemical reactions. Using lasers, new chemical compounds can be created by breaking bonds between atoms are molecules.
4. Photography
Lasers can be used to get 3-D lens less photography. Lasers are also used in the construction of holograms.
5. Industry
Lasers can be used to blast holes in diamonds and hard steel. Lasers are also used as a source of intense heat Carbon dioxide laser is used for cutting drilling of metals and non-metals, such as ceramics plastics glass etc. High power lasers are used to weld or melt any material. Lasers are also used to cut teeth in saws and test the quality of fabric. It is used to cut glass and quartz, used in electronic industries for trimming the components of Integrated Circuits (ICs). Lasers are used for heat treatment in the automotive industry. Laser light is used to collect the information about the prefixed prices of various products in shops and business establishments from the bar code printed on the product. Ultraviolet lasers are used in the semiconductor industries for photolithography. Photolithography is the method used for manufacturing printed circuit board (PCB) and microprocessor by using ultraviolet light. It is also used to drill aerosol nozzles and control orifices within the required precision.
6. Medicine
Pulsed neodymium laser is employed in the treatment of liver cancer. Argon and carbon dioxide lasers are used in the treat men of liver and lungs. Lasers used in the treatment of Glaucoma.
Lasers used in endoscopy to scan the inner parts of the stomach. Lasers used in the elimination of moles and tumors which are developing in the skin tissue and hair removal. It is also used for bloodless surgery.
Lasers are used to destroy kidney stones, in cancer diagnosis and therapy also used for eye lens curvature corrections. Lasers are used to study the internal structure of microorganisms and cells. It is used to create plasma. Lasers are used to remove the caries or decayed portion of the teeth.
7. Military
Lasers can be used as a war weapon. High energy lasers are used to destroy the enemy air-crofts and missiles. Lasers can be used in the detection and ranging likes RADAR. Laser range finders are used to determine the distance to an object. The ring laser gyroscope is used for sensing and measuring very small angle of rotation of the moving objects.
Lasers can be used as a secretive illuminators for reconnaissance during night with high precision.
8. Scientific research
Lasers are used in the field of 3D-photography Lasers used in Recording and reconstruction of hologram. Lasers are employed to create plasma. Lasers are used in Raman spectroscopy to identify the structure of the molecule and to count the number of atoms in a substance. Lasers are used in the Michelson- Morley experiment. A laser beam is used to confirm Doppler shifts in frequency for moving objects. A laser helps in studying the Brownian motion of particles. With the help of a helium-neon laser, it was proved that the velocity of light is same in all directions. Lasers are used to measure the pollutant gases and other contaminants of the atmosphere. Lasers help in determining the rate of rotation of the earth accurately. Lasers are used for detecting earthquakes and underwater nuclear blasts. A gallium arsenide diode laser can be used to setup an invisible fence to protect an area.
OPTICAL FIBRE
A cable that is used to transmit the data through fibres (threads) or plastic (glass) is known as an optical fibre cable. This cable includes a pack of glass threads that transmits modulated messages over light waves.
Principle: Optical Fibre works on the principle of Total Internal Reflection.
Principle: Optical Fibre works on the principle of Total Internal Reflection.
Total internal reflection:-
When the light ray travels from denser medium to rarer medium the refracted ray bends away from the normal. When the angle of incidence is greater than the critical angle, the refracted ray again reflects into the same medium. This phenomenon is called total internal reflection. The refracted ray bends towards the normal as the ray travels from rarer medium to denser medium. The refracted ray bends away from the normal as it travels from denser medium to rarer medium.
|
Figure 17: Total Internal Reflection
When light passes from a medium with one index of refraction (m1), to another medium with a lower index of refraction (m2), it bends or refracts away from an imaginary line perpendicular to the surface (normal line). As the angle of the beam through m1 becomes greater with respect to the normal line, the refracted light through m2 bends further away from the line.
At one particular angle (critical angle), the refracted light will not go into m2, but instead will travel along the surface between the two media (sine [critical angle] = n2/n1 where n1 and n2 are the indices of refraction [n1 is greater than n2]). If the beam through m1 is greater than the critical angle, then the refracted beam will be reflected entirely back into m1 (total internal reflection), even though m2 may be transparent.
In physics, the critical angle is described with respect to the normal line. In fiber optics, the critical angle is described with respect to the parallel axis running down the middle of the fiber. Therefore, the fiber-optic critical angle = (90 degrees - physics critical angle).
In an optical fiber, the light travels through the core (m1, high index of refraction) by constantly reflecting from the cladding (m2, lower index of refraction) because the angle of the light is always greater than the critical angle. Light reflects from the cladding no matter what angle the fiber itself gets bent at, even if it's a full circle.
Because the cladding does not absorb any light from the core, the light wave can travel great distances. However, some of the light signal degrades within the fiber, mostly due to impurities in the glass. The extent that the signal degrades depends upon the purity of the glass and the wavelength of the transmitted light
When the angle of incidence (θ1) is progressively increased, there will be progressive increase of refractive angle (θ2). At some condition (θ1) the refractive angle (θ2) becomes 90o to the normal. When this happens the refracted light ray travels along the interface. The angle of incidence (θ1) at the point at which the refractive angle (θ1) becomes 90 degree is called the critical angle.
It is denoted by θc. The critical angle is defined as the minimum angle of incidence (θ1) at which the ray strikes the interface of two media and causes an angle of refraction (θ2) equal to 90o. Figure 17 shows critical angle refraction
Hence at critical angle θ1= θc and θ2= 90o .
Using Snell‘s law: n1 sin θ1 = n2 sin θ2
n1 sin θc = n2 sin90o
sin θc = n2 / n1
θc = sin-1 (n2 / n1)
The actual value of critical angle is dependent upon combination of materials present on each side of boundary.
CHARACTERISTICS OF OPTICAL FIBRE
- It has a large bandwidth.
- The optical frequency of 2 x 1014 Hz can be used and hence the system has higher bandwidth.
- Thus optical fibres have greater information-carrying capacity due to greater bandwidth.
- In an optical fibre system transmission losses are as low as 0.1 db/km.
- Optical fibre is of small size and lightweight as compared to electrical fibre.
- Optical fibre communication is free from electromagnetic interference.
- Optical fibre does not carry high voltage and current hence they are safer than electrical cable.
- Optical Fibres are flexible and have high tensile strength. Thus can be bent or twisted easily.
|
Figure 18: Optical Fibre
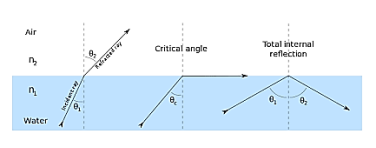
CONSTRUCTION OF OPTICAL FIBRE
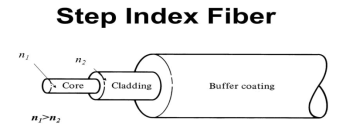
It consists of a very thin fibre of silica or glass or plastic of a high refractive index called the core. The core has a diameter of 10 um to 100 um. The core is enclosed by a cover of glass or plastic called cladding. The refractive index of the cladding is less than that of the core (which is a must condition for the working of the optical fibre). The difference between the two indicates is very small of order 10-3. The core and the cladding are enclosed in an outer protective jacket made of plastic to provide strength to the optical fibre. The refractive index can change from core to cladding abruptly (as in step-index fibre) or gradually (as in graded-index fibre).
|
Figure 19 : Representation of Optical Fibre
WORKING OF OPTICAL FIBRE
When a ray of light is incident on the core of the optical fibre at a small angle, it suffers refraction and strikes the core-cladding interface, As the diameter of the fibre is very small hence the angle of incidence is greater than the critical angle. Therefore, the ray suffers total internal reflection at the core-cladding interface and strikes the opposite interface. At this interface also, the angle of incidence is greater than the critical angle, so it again suffers total internal reflection. Thus, the ray of light reaches the other end of the fibre after suffering repeated total internal reflections along the length of the fibre. At the other end, the ray suffers refraction and emerges out of the optical fibre.
We can see that the light travels in the core in a guided manner. Hence the communication through the optical fibre is sometimes referred to as an optical waveguide.
Key Takeaways
A cable that is used to transmit the data through fibres (threads) or plastic (glass) is known as an optical fibre cable. This cable includes a pack of glass threads that transmits modulated messages over light waves.
Principle: Optical Fibre works on the principle of Total Internal Reflection.
It consists of a very thin fibre of silica or glass or plastic of a high refractive index called the core. The core has a diameter of 10 um to 100 um.
The core is enclosed by a cover of glass or plastic called cladding. The refractive index of the cladding is less than that of the core.
The core and the cladding are enclosed in an outer protective jacket made of plastic to provide strength to the optical fibre.
Light propagates inside an optical fiber by virtue of multiple TIRs at the core-cladding interface. The refractive index of the core glass is greater than that of the cladding. This meets the first condition for a TIR. All the light energy that is launched into the optical fiber through its tip does not get guided along the fiber. Only those light rays propagate through the fiber which is launched into the fiber at such an angle that the refracted ray inside the core of the optical fiber is incident on the core-cladding interface at an angle greater than the critical angle of the core with respect to the cladding.
1. Optical fiber is basically a solid glass rod. The diameter of rod is so small that it looks like a fiber.
2. Optical fiber is a dielectric waveguide. The light travels like an electromagnetic wave inside the waveguide. The dielectric waveguide is different from a metallic waveguide which is used at microwave and millimeter wave frequencies.
3. In a metallic waveguide, there is a complete shielding of electromagnetic radiation but in an optical fiber the electromagnetic radiation is not just confined inside the fiber but also extends outside the fiber.
4. The light gets guided inside the structure, through the basic phenomenon of total internal reflection.
5. The optical fiber consists of two concentric cylinders; the inside solid cylinder is called the core and the surrounding shell is called the cladding. (See Fig 12)
|
Figure 20: Schematic of an optical fiber
6. For the light to propagate inside the fiber through total internal reflections at core-cladding interface, the refractive index of the core must be greater than the refractive index of the cladding. That is n1>n2.
SIMPLE RAY MODEL
|
Figure 21: (optical fiber with core, cladding and total internally reflected ray)
For propagation of light inside the core there are two possibilities.
1. A light ray is launched in a plane containing the axis of the fiber. We can then see the light ray after total internal reflection travels in the same plane i.e., the ray is confined to the plane in which it was launched and never leave the plane. In this situation the rays will always cross the axis of the fiber. These are called the Meridional rays. (Figure 21)
2. The other possibility is that the ray is not launched in a plane containing the axis of the fiber.
For example if the ray is launched at some angle such that it does not intersect the axis of the fiber, then after total internal reflection it will go to some other plane. We can see that in this situation the ray will never intersect the axis of the fiber. The ray essentially will spiral around the axis of fiber. These rays are called the Skew rays.
So it can be concluded that if the light is to propagate inside an optical fiber it could be through two types of rays
a) Meridional rays: The rays which always pass through the axis of fiber giving high optical intensity at the center of the core of the fiber.
b) Skew Rays: The rays which never intersect the axis of the fiber, giving low optical intensity at the center and high intensity towards the rim of the fiber.
Propagation of Meridional Rays
|
Figure 22: Propagation of Meridional Rays
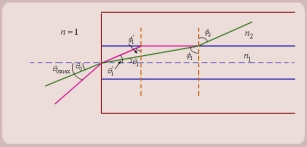
Let us consider figure 22. A ray is launched from outside (air) at an angle θ0 , from the axis of the fiber.
The question is, under what conditions the ray is ultimately guided inside the core due to total internal reflections at the core cladding boundary.
Let the ray makes an angle θ1 with the axis of the fiber inside the core, and let the ray make an angle ϕ1 with core -cladding interface. Let ϕ2 be the angle of refraction in the cladding.
If ϕ1 < critical angle the ray is refracted in cladding. The ray which goes to cladding is lost and is not useful for communication. The ray which is confined to the core is useful for optical communication.
Now as we increase the launching angle θ0, the angle θ1 also increases. Since θ1 + ϕ1 =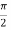 
ϕ1 decreases and at some point becomes less than the critical angle. When ϕ1 equals the critical angle, ϕ2 equals 
. The maximum launching angle then corresponds to ϕ2 =
.
Let us apply Snell’s law at the launching point and at the core-cladding interface for the maximum launching angle θ0max. For this case let θ1 = θ’1 and ϕ1 = ϕ’1
we then have
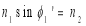(since 
)
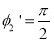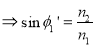
now,
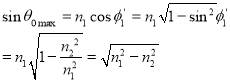
So the sine of the maximum angle at which the ray will be guided inside the fiber is given by square root of the difference of squares of the refractive indices of the core and cladding. The quantity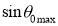
is called the numerical aperture of an optical fiber. The NA is a measure of the power launching efficiently of an optical fiber.
Key Takeaways
Light propagates inside an optical fiber by virtue of multiple TIRs at the core-cladding interface.
The refractive index of the core glass is greater than that of the cladding.
Optical fiber is a dielectric waveguide. The light travels like an electromagnetic wave inside the waveguide.
If the light is to propagate inside an optical fiber it could be through two types of rays; Meridional rays and Skew Rays.
The quantity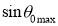
is called the numerical aperture of an optical fiber. The NA is a measure of the power launching efficiently of an optical fiber. It is given by NA = ( n12- n22 )1/2
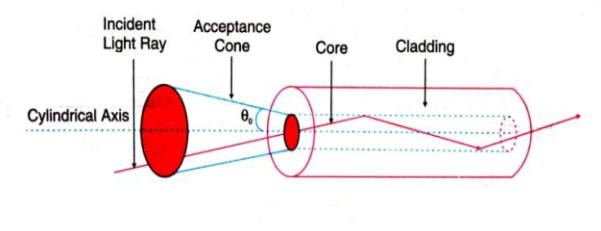
ACCEPTANCE ANGLE
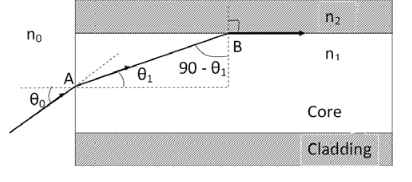
Definition:- Acceptance angle is defined as the maximum angle of incidence at the interface of air medium and core medium for which the light ray enters into the core and travels along with the interface of core and cladding.
Let n0 be the refractive indices of air
n1 be the refractive indices of core
n2 be the refractive indices of cladding
|
Figure 23: Acceptance angle
Let a light ray OA is an incident on the interface of air medium and core medium with an angle of incidence θ0
The light ray refracts into the core medium with an angle of refraction θ1 and the refracted ray AB is again incident on the interface of core and cladding with an angle of the incident (90- θ1)
If (90- θ1) is equal to the critical angle of core and cladding media then the ray travels along with the interface of core and cladding along the path BC. If the angle of the incident at the interface of air and core θ1< θ0 then (90- θ1) will be greater than the critical angle. Therefore,
The total internal reflection takes place.
According to Snell’s law at point A
n0 Sin θ0 = n1 Sin θ1
Sin θ0= (n1 / n0) Sin θ1 ………(1)
According to Snell’s law at point B
n1 Sin(90- θ1) = n2 Sin90 ………(2)
n1 Cosθ1 = n2 as (Sin90=1)
Cosθ1 = n2 /n1
Sinθ1 = (1-Cos2 θ1)1/2
Sinθ1= (1- (n2 /n1)2)1/2
Sinθ1= ( n12- n22 )1/2/ n1 ………(3)
We know Sin θ0= (n1 / n0) Sin θ1 from equation (1)
Substitute the value of Sinθ1 from equation (3)
Sinθ0= (n1 / n0) *( n12- n22 )1/2/ n1
On simplification
Sinθ0= ( n12- n22 )1/2/ n0
θ0=Sin-1 ( n12- n22 )1/2/ n0
Acceptance Angle is θ0=Sin-1 ( n12- n22 )1/2/ n0 ………(4)
ACCEPTANCE CONE
Acceptance angle is the maximum angle that a light ray can have relative to the axis of the fibre and propagate down the fibre. Thus, only those rays that are incident on the face of the fibre making angles less than θ0 will undergo repeated total internal reflections and reach the other end of the fibre. Hence, larger acceptance angles make it easier to launch light into fibre.
|
Figure 24: Acceptance cone
In three dimensions, the light rays contained within the cone having a full angle 2θ0 are accepted and transmitted along with the fibre as shown in figure 24. Therefore, the cone is called the acceptance cone. Light incident at an angle beyond θ0 refracts through the cladding and corresponding optical energy is lost.
NUMERICAL APERTURE
Definition: -Numerical aperture is defined as the light gathering capacity of an optical fibre and it is directly proportional to the acceptance angle. Numerically it is equal to the sin of the acceptance angle.
NA = Sin(acceptance angle)
NA = Sin {Sin-1 (( n12- n22 )1/2/ n0)} from equation (4)
NA = (( n12- n22 )1/2/ n0) ………(5)
If the refractive index of the air medium is unity i.e. n0=1 put in (5)
NA = ( n12- n22 )1/2 ………(6)
Fractional change in refractive index
∆= (n1- n2)/ n1
n1∆ = (n1- n2) ………(7)
from equation (6), we have
NA = {( n1- n2 )( n1+n2 )}1/2
NA = { n1∆ (n1+n2 )}1/2 as n1∆ = (n1- n2) by Eq(7)
NA = { n1∆ 2n1}1/2 n1 ≈ n2, so n1+n2 =2n1
NA = n1{2∆}1/2
This gives the relation between Numerical aperture and Fractional change in refractive index.
Key Takeaways
Acceptance angle is defined as the maximum angle of incidence at the interface of air medium and core medium for which the light ray enters into the core and travels along with the interface of core and cladding.
Acceptance Angle is given by θ0=Sin-1 ( n12- n22 )1/2/ n0
In three dimensions, the light rays contained within the cone having a full angle 2θ0 are accepted and transmitted along with the fibre. Therefore, the cone is called the acceptance cone.
Numerical aperture is defined as the light gathering capacity of an optical fibre and it is directly proportional to the acceptance angle. Numerically it is equal to the sin of the acceptance angle.
Numerical aperture is given by NA = n1{2∆}1/2
The types of optical fibres depend on the refractive index, materials used, and mode of propagation of light.
The classification based on the materials used is as follows:
Plastic Optical Fibres: The polymethylmethacrylate is used as a core material for the transmission of light.
Example:
Core: polymethyl methacrylate : Cladding: Co- Polymer
Core: Polystyrene : Cladding: Methyl methacrylate
Glass Fibres: It consists of extremely fine glass fibres.
Example:
Core: SiO2 Cladding: SiO2
Core: GeO2- SiO2 Cladding: SiO2
The classification based on the mode of propagation of light is as follows:
Mode of propagation:
Light propagates as electromagnetic waves through an optical fibre. All waves, having ray directions above the critical angle will be trapped within the fibre due to total internal reflection. However, all such waves do not propagate through the fibre. Only certain ray directions are allowed to propagate. The allowed directions correspond to the modes of the fibre. In simple terms, modes can be visualized as the possible number of paths of light in an optical fibre.
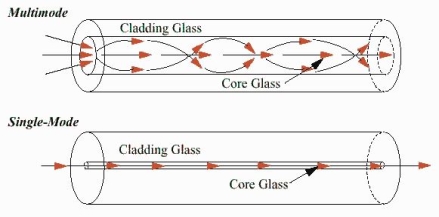
Single-Mode Fibres:
These fibres are used for long-distance transmission of signals. In general, the single-mode fibres are step-index fibres. These types of fibres are made from doped silica. It has a very small core diameter so that it can allow only one mode of propagation and hence called single-mode fibres.
The cladding diameter must be very large compared to the core diameter. Thus in the case of single-mode fibre, the optical loss is very much reduced. The structure of a single-mode fibre is given below.
Structure:
Core diameter: 5-10μm
Cladding diameter: Generally around 125μm
Protective layer: 250 to 1000μm
Numerical aperture: 0.08 to 0.10
Bandwidth: More than 50MHz km.
Application:
Because of high bandwidth, they are used in long-haul communication systems.
|
Figure 25: Single Mode and Multimode Fibre
Multimode Fibres:
These fibres are used for short-distance transmission of signals. The multi-mode fibres are useful in manufacturing both for step-index and graded-index fibres. The multi-mode fibres are made by multi-component glass compounds such as Glass – Clad Glass, Silica – Clad – Silica, doped silica, etc. Here the core diameter is very large compared to single-mode fibres, so that it can allow many modes to propagate through it and hence called Multi-mode fibres. The cladding diameter is also larger than the diameter of the single-mode fibres. The structure of the multimode fibre is as shown in the figure above.
Structure:
Core diameter : 50-350μm
Cladding diameter : 125μm - 500μm
Protective layer : 250 to 1100μm
Numerical aperture : 0.12 to 0.5
Bandwidth : Less than 50MHz km.
The total number of modes possible for such an electromagnetic waveguide is
|
Application:
Because of its less bandwidth, it is very useful in short-haul communication systems.
The classification based on the refractive index is as follows:
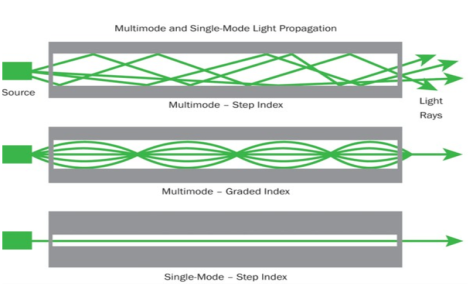
Step Index Single-mode Fibres
It consists of a core surrounded by the cladding, which has a single uniform index of refraction. Step index-single mode fibres: A single-mode step-index fibre consists of a very thin core of uniform refractive index surrounded by a cladding of refractive index lower than that of the core. The refractive index abruptly changes at the core-cladding boundary. Light travels along a side path, i.e., along the axis only. So zero-order modes are supported by Single Mode Fibre.
|
Figure 26: Step Index Single-mode Fibres
Step Index-Multimode fibres
A multimode step-index fibre consists of a core of uniform refractive index surrounded by a cladding of refractive index lower than that of the core. The refractive index abruptly changes at the core-cladding boundary. The core is of large diameter. Light follows zigzag paths inside the fibre. Many such zigzag paths of propagation are permitted in Multi-Mode Fibre. The Numerical Aperture of a Multi-mode fibre is larger as the core diameter of the fibre is larger
|
Figure: 27 Step Index-Multimode fibres
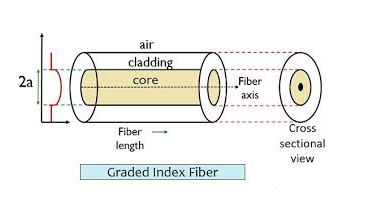
Graded Index Fibres:
The refractive index of the optical fibre decreases as the radial distance from the fibre axis increases. GRIN fibre is one in which the refractive index varies radially, decreasing continuously in a parabolic manner from the maximum value of n1, at the center of the core to a constant value of n2 at the core-cladding interface.
In graded-index fibre, light rays travel at different speeds in different parts of the fibre because the refractive index varies throughout the fibre. Near the outer edge, the refractive index is lower. As a result, rays near the outer edge travel faster than the rays at the center of the core. Because of this, rays arrive at the end of the fibre at approximately the same time. In effect light rays that arrive at the end of the fibre are continuously refocused as they travel down the fibre. All rays take the same amount of time in traversing the fibre. This leads to small pulse dispersion.
Figure 28: Graded Index Fibres
|
For a parabolic index fibre, the pulse dispersion is reduced by a factor of about 200 in comparison to step-index fibre. It is because of this reason that first and second-generation optical communication systems used near parabolic index fibres.
Key Takeaways
The types of optical fibres depend on the refractive index, materials used, and mode of propagation of light.
The classification based on the materials is of two type plastic optical fibres and glass fibres.
The classification based on the mode of propagation is of two type single mode fibre and multimode fibre.
The classification based on the refractive index is of three types step index single mode fibre, step index multimode fibre and graded index fibre.
NORMALIZED FREQUENCY Or V-NUMBER
An optical fibre is characterized by one more important parameter, known as V-number which is more generally called normalized frequency of the fibre. It is given by the relation
V – number determines how many modes a fiber can support, it is given by,
V =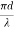 
NA
Where d is the diameter of the core,
l is the wavelength of light used
NA is the numerical aperture of the fibre.
V =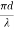
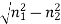
Or
V =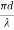
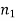
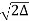
If V ≤ 2.405, then the fibre is single mode fibre (SMF)
If V > 2.405, then the fibre is multimode fibre (MMF)
Example: Consider a multimode step index fibre with n1 = 1.53 and n2 = 1.50 and λ= 1μm. If the core radius = 50 μm then calculate the normalized frequency of the fibre (V) and the number of guided mode.
Solution:
d = 2r = 2 x 50 x 10-6 m
V =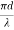 
NA =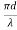
= 
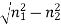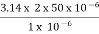
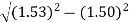
=94.72= normalized frequency
Total number of guided mode = M = V2/2 = 4486.
One of the important property of optical fiber is signal attenuation. It is also known as fiber loss or signal loss. The signal attenuation of fiber determines the maximum distance between transmitter and receiver. The attenuation also determines the number of repeaters required, maintaining repeater is a costly affair. Another important property of optical fiber is distortion mechanism. As the signal pulse travels along the fiber length it becomes broader. After sufficient length the broad pulses starts overlapping with adjacent pulses. This creates error in the receiver. Hence the distortion limits the information carrying capacity of fiber.
Attenuation in Optical Fibres
Attenuation is a measure of decay of signal strength or loss of light power that occurs as light pulses propagate through the length of the fibre
In optical fibres the attenuation is mainly caused by two physical factors absorption and scattering losses. Absorption is because of fibre material and scattering due to structural imperfection within the fibre.
Nearly 90 % of total attenuation is caused by Rayleigh scattering only. Micro bending of optical fibre also contributes to the attenuation of signal.
The rate at which light is absorbed is dependent on the wavelength of the light and the characteristics of particular glass. Glass is a silicon compound; by adding different additional chemicals to the basic silicon dioxide the optical properties of the glass can be changed.
The Rayleigh scattering is wavelength dependent and reduces rapidly as the wavelength of the incident radiation increases.
The attenuation of fibre is governed by the materials from which it is fabricated, the manufacturing process and the refractive index profile chosen.
Attenuation loss is measured in dB/km.
As attenuation leads to a loss of power along the fibre, the output power is significantly less than the couples power. Let the couples optical power is P (0) i.e. at origin (z =0). Then the power at distance z is given by,
P(z) = P(0)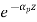 
Where, αp is fibre attenuation constant (per km).
αp = 
ln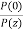 
αp (dB/km) = 10. 
log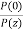 
αp (dB/km) = 4.343 αp/km
This parameter is known as fibre loss or fibre attenuation. Attenuation is also a function of wavelength.
Example: When mean optical power launched into an 8 km length of fibre is 12 μW, the mean optical power at the fibre output is 3 μW. Determine
Overall signal attenuation in dB.
The overall signal attenuation for a 10 km optical link using the same fibre with splices at 1 km intervals, each giving an attenuation of 1 dB.
Solution:
Given: z=8km
P (0) = 120 μW
P(z) = 3 μW
Overall attenuation is given by,
αp (dB/km) = 10. log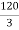 
= 16.02
Overall attenuation for 10 km,
Attenuation per km = αp (dB/km)
= 
= 
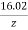
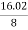= 2.00 dB/km
Attenuation in 10 km link = 2.00 x 10 = 20 dB
In 10 km link there will be 9 splices at 1 km interval. Each splices introducing attenuation of 1 dB.
Total attenuation = 20 dB + 9 dB = 29 dB
Losses in optical fiber:
Absorption loss
Scattering loss
Radiative loss or Bending loss
Dispersion loss
1. Absorption:
Absorption loss is because of the material composition and fabrication process of fiber. Absorption loss results in dissipation of some optical power as hear in the fiber cable. Although glass fibres are extremely pure, some impurities still remain as residue after purification. The amount of absorption by these impurities depends on their concentration and light wavelength.
Usually absorption of light occurs due to imperfections of the atomic structure such as missing molecules, (OH-), hydroxyl ions, high density cluster of atoms etc., which absorbs light.
a. Intrinsic absorption: Intrinsic absorption in the ultraviolet region is caused by electronic absorption bands. Basically, absorption occurs when a light particle (photon) interacts with an electron and excites it to a higher energy level. The main cause of intrinsic absorption in the infrared region is the characteristic vibration frequency of atomic bonds. In silica glass, absorption is caused by the vibration of silicon-oxygen (Si-O) bonds. The interaction between the vibrating bond and the electromagnetic field of the optical signal causes intrinsic absorption. Light energy is transferred from the electromagnetic field to the bond.
b. Extrinsic absorption: Extrinsic absorption is much more significant than intrinsic Caused by impurities introduced into the fiber material during manufacture – Iron, nickel, and chromium Caused by transition of metal ions to higher energy level. Modern fabrication techniques can reduce impurity levels.
2. Scattering:
Basically, scattering losses are caused by the interaction of light with density fluctuations within a fiber. Density changes are produced when optical fibres are manufactured.
Linear Scattering Losses: Linear scattering occurs when optical energy is transferred from the dominant mode of operation to adjacent modes. It is proportional to the input optical power injected into the dominant mode. Scattering is also a wavelength dependent loss, which occurs inside the fibres. Since the glass is used in fabrication of fibres, the disordered structure of glass will make some variations in the refractive index inside the fiber. As a result, if light is passed through the atoms in the fiber, a portion of light is scattered (elastic scattering). This type of scattering is called Raleigh scattering. Linear scattering is divided into two categories: Mie scattering and Rayleigh scattering.
Non- Linear Scattering Losses: Scattering loss in a fiber also occurs due to fiber non-linearity’s i.e. if the optical power at the output of the fiber does not change proportionately with the power change at the input of the fiber, the optical fiber is said to be operating in the non-linear mode. Non- Linear scattering is divided into two categories: Stimulated Raman Scattering and Stimulated Brillouin Scattering.
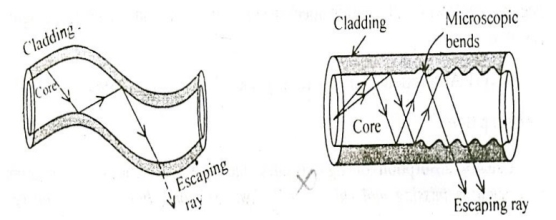
3. Radiative loss or Bending loss
Radiative losses also called bending losses. Radiative loss occurs when the fibre is curved. Radiative loss occurs in fibres due to bending of finite radius of curvature in optical fibres. The types of bends are
Macroscopic bends
Microscopic bends
a. Macroscopic bends: If the radius of the core is large compared to fiber diameter, it may cause large-curvature at the position where the fiber cable turns at the corner. At these corners the light will not satisfy the condition for total internal reflection and hence it escapes out from the fiber. This is called as macroscopic / macro bending losses. Also note that this loss is negligible for small bends.
|
Figure 29: Bending loss
b. Microscopic bends: Micro-bends losses are caused due to non-uniformities or micro bends inside the fiber as shown. This micro bends in fiber appears due to non-uniform pressures created during the cabling of the fiber or even during the manufacturing itself. This lead to loss of light by leakage through the fiber.
Dispersion Loss
Dispersion: A light pulse launched into a fibre decreases in the fibre. It also spreads during its travel. The pulse received at the output is wider than input pulse.
It means that the pulse becomes distorted as it is propagated through the fibre. Such a distortion arises due to dispersion effects.
Dispersion is typically measured in Nano seconds per kilometre (ns/km).
There are three mechanisms which contribute to the distortion of the light pulse in a fibre. They are known as:
- Material dispersion
- Wave guide dispersion
- Chromatic Dispersion
- Modal Dispersion
Material Dispersion
Material dispersion is also called as chromatic dispersion. Material dispersion exists due to change in index of refraction for different wavelengths. A light ray contains components of various wavelengths. The time delay is different for different wavelength components. This results in time dispersion of pulse at the receiving end of fibre.
Light waves of different wavelengths travel at different speeds in a medium. The short wavelength waves travel slower than long wavelength waves. Consequently, narrow pulses of light tend to broaden as they travel down the optical fibre. This is known as material dispersion.
The material dispersion for unit length (L = 1) is given by
D =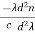 
Where c = Light velocity
λ = Center wavelength
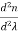= Second derivative of index of refraction w.r.t wavelength.
Negative sign shows that the upper sideband signal (lowest wavelength) arrives before the lower sideband (highest wavelength).
The unit of dispersion is: ps/nm/km. The amount of material dispersion depends upon the chemical composition of glass.
Example: An LED operating at 850 nm has a spectral width of 45 nm. What is the pulse spreading in ns/km due to material dispersion?
Solution:
Given: λ = 850 nm
σ = 45 nm
R.M.S pulse broadening due to material dispersion is given by,
σm= σLM
Considering length L = 1 metre
Dmat =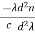 
For LED source operating at 850 nm,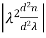 
= 0.025
M =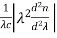 
by substituting all values we have
M = 9.8 ps/nm/km
σm= 441 ns/km
Waveguide Dispersion
Waveguide dispersion is caused by the difference in the index of refraction between the core and cladding, resulting in a ‘drag’ effect between the core and cladding portions of the power.
Waveguide dispersion is significant only in fibres carrying fewer than 5-10 modes. Since multimode optical fibres carry hundreds of modes, they will not have observable waveguide dispersion.
The group delay (τwg) arising due to waveguide dispersion.
τwg =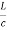 
[ n2 +n2 ∆ 
]
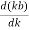Where, b = Normalized propagation
constant k = 2π / λ (group velocity)
Normalized frequency V,
V = ka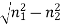 
τwg =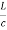 
[ n2 +n2 ∆ 
]
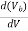The second term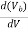 
is waveguide dispersion and is mode dependent term.
As frequency is a function of wavelength, the group velocity of the energy varies with frequency. This produces additional losses (waveguide dispersion). The propagation constant (b) varies with wavelength, the causes of which are independent of material dispersion.
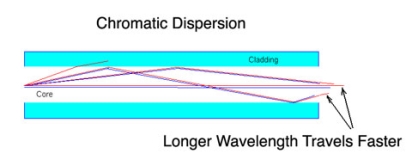
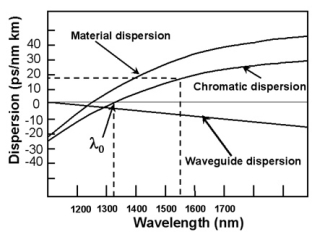
Chromatic Dispersion
The combination of material dispersion and waveguide dispersion is called chromatic dispersion. These losses primarily concern the spectral width of transmitter and choice of correct wavelength.
|
Figure 30: Chromatic Dispersion
Material dispersion and waveguide dispersion effects vary in opposite senses as the wavelength increased, but at an optimum wavelength, two effects almost cancel each other and chromatic dispersion is at minimum. Attenuation is therefore also at minimum and makes highly attractive Operating wavelength.
|
Figure 31: Dispersion-Wavelength variation
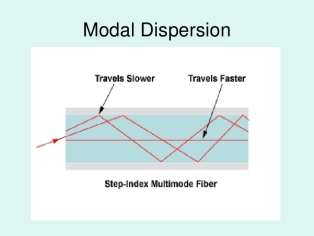
Modal Dispersion
As only a certain number of modes can propagate down the fibre, each of these modes carries the modulation signal and each one is incident on the boundary at a different angle, they will each have their own individual propagation times. The net effect is spreading of pulse; this form of dispersion is called modal dispersion.
|
Figure 32: Modal Dispersion
Modal dispersion takes place in multimode fibres. It is moderately present in graded index fibres and almost eliminated in single mode step index fibres.
Modal dispersion is given by
∆tmodal =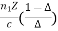 
Where ∆tmodal = Dispersion
n1= Core refractive index
Z = Total fibre length
c = Velocity of light in air.
The above equation can also be written as
∆tmodal =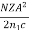 
The modal dispersion ∆tmodal describes the optical pulse spreading due to modal effects optical pulse width can be converted to electrical rise time through the relationship.
tr mod = 0.44 (∆tmodal) πr2
Key Takeaways
Attenuation is a measure of decay of signal strength or loss of light power that occurs as light pulses propagate through the length of the fibre
In optical fibres the attenuation is mainly caused by two physical factors absorption and scattering losses. Absorption is because of fibre material and scattering due to structural imperfection within the fibre.
Nearly 90 % of total attenuation is caused by Rayleigh scattering only. Micro bending of optical fibre also contributes to the attenuation of signal.
Losses in optical fiber can be Absorption loss, scattering loss, Radiative loss or Bending loss, Dispersion loss.
Absorption loss is because of the material composition and fabrication process of fiber. It can be Intrinsic absorption and Extrinsic absorption.
Scattering losses are caused by the interaction of light with density fluctuations within a fiber. It can be Linear scattering loss and Non- Linear Scattering Losses.
Radiative loss occurs in fibres due to bending of finite radius of curvature in optical fibres. The types of bends are Macroscopic bends and Microscopic bends.
It means that the pulse becomes distorted as it is propagated through the fibre. Such a distortion arises due to dispersion effects.
The pulse becomes distorted as it is propagated through the fibre. Such a distortion arises due to dispersion effects. There are three mechanisms which contribute to the distortion of the light pulse in a fibre. They are known as Material dispersion, Wave guide dispersion Chromatic Dispersion and Modal Dispersion.
Optical fibres are extensively used in a communication system.
Optical fibres are in the exchange of information between different computers
Optical fibres are used for the exchange of information in cable televisions, space vehicles, submarines, etc.
Optical fibres are used in the industry in security alarm systems, process control, and industrial auto machine.
Optical fibres are used in pressure sensors in biomedical and engine control.
Optical fibres are used in medicine, in the fabrication of endoscopy for the visualization of internal parts of the human body.
Sensing applications of optical fibres are Displacement sensor, Fluid level detector, Liquid level sensor, Temperature/pressure sensor, and Chemical sensors
Medical applications of optical fibres are Gastroscopy, Orthoscopic, Couldoscope, Peritonescope, and Fibrescope.
Let us discuss in detail the advantages of fibre optic communication
Optical fibre communication has more advantages than conventional communication.
1. Enormous Bandwidth
2. Low Transmission Loss
3. Electric Isolation
4. Signal Security
5. Small Size and Less Weight
6. Immunity Cross Talk
1. Enormous bandwidth: - The information-carrying capacity of a transmission system is directly proportional to the frequency of the transmitted signals. In the coaxial cable transmission, the bandwidth range is up to around 500MHz only. Whereas in optical fibre communication, the bandwidth range is large as 105 GHz.
2. Low transmission loss: - The transmission loss is very low in optical fibres (i.e. KmdB/2.0) than compare with the conventional communication system. Hence for long-distance communication fibres are preferred.
3. Electric isolation: - Since fibre optic materials are insulators, they do not exhibit earth and interface problems. Hence communicate through fibre even in an electrical dangerous environment.
4. Signal security: - The transmitted signal through the fibre does not radiate, unlike the copper cables, a transmitted signal cannot be drawn from fibre without tampering with it. Thus the optical fibre communication provides 100% signal security.
5. Small size and less weight: - The size of the fibre ranges from 10μm to 50μm, which is very small. The space occupied by the fibre cable is negligibly small compared to conventional electrical cables. Optical fibres are light in weight.
6. Immunity cross-talk: - Since the optical fibres are dielectric waveguides, they are free from any electromagnetic interference and radio frequency interference. Since optical interference among different fibres is not possible, cross talk is negligible even many fibres are cabled together.
Disadvantages of Optical Fibre
The disadvantages of optical fibre include the following
The main disadvantages of these cables are installation is expensive and difficult to fix together.
The optical fibre cables are very difficult to merge & there will be a loss of the beam within the cable while scattering.
Fibre optic cables are compact and highly vulnerable while fitting
These cables are more delicate than copper wires.
Special devices are needed to check the transmission of fibre cables.
Reference Books
- Fundamentals of Optics-Jenkins and White. McGraw Hill Publication
- A Text Book of Optics Subrahmanyam, BrijIal, S. Chand Publication
- Optics by Ajay Ghatak
- Engineering physics - Avadhanalu and Kshirsagar, S. Chand Publication
