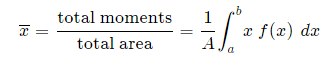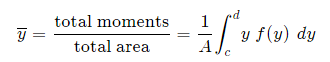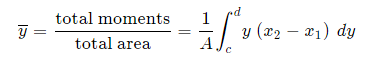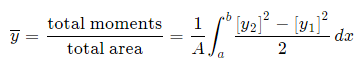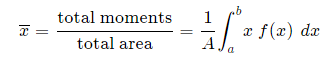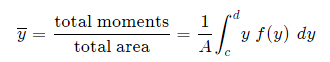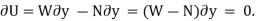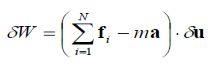UNIT-3
Centroids and Moments of Inertia
In Geometry, the centroid is an important concept related to a triangle. A triangle is a three-sided bounded figure with three interior angles. Based on the sides and angles, a triangle can be classified into different types such as
- Scalene triangle
- Isosceles triangle
- Equilateral triangle
- Acute-angled triangle
- Obtuse-angled triangle
- Right-angled triangle
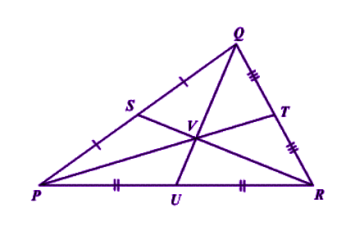
The centroid is the centre point of the object. The point in which the three medians of the triangle intersect is known as the centroid of a triangle. It is also defined as the point of intersection of all the three medians. The median is a line that joins the midpoint of a side and the opposite vertex of the triangle. The centroid of the triangle separates the median in the ratio of 2: 1. It can be found by taking the average of x- coordinate points and y-coordinate points of all the vertices of the triangle.
The centroid theorem states that the centroid of the triangle is at 2/3 of the distance from the vertex to the mid-point of the sides.
|
Fig 1
Suppose PQR is a triangle having a centroid V. S, T and U are the midpoints of the sides of the triangle PQ, QR and PR, respectively. Hence as per the theorem;
QV = 2/3 QU,
PV = 2/3 PT and RV = 2/3 RS
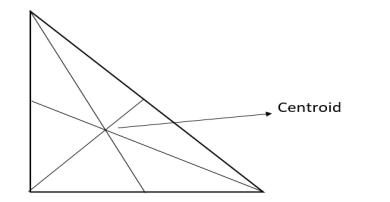
Centroid of a Right Angle Triangle
The centroid of a right angle triangle is the point of intersection of three medians, drawn from the vertices of the triangle to the midpoint of the opposite sides.
|
Fig 2
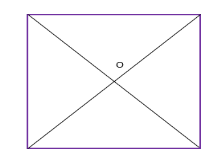
The point where the diagonals of the square intersect each other is the centroid of the square. As we all know, the square has all its sides equal. Hence it is easy to locate the centroid in it. See the below figure, where O is the centroid of the square.
|
Fig 3
The properties of the centroid are as follows:
- The centroid is the centre of the object.
- It is the centre of gravity.
- It should always lie inside the object.
- It is the point of concurrency of the medians.
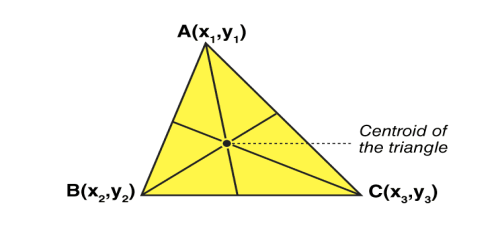
Let’s consider a triangle. If the three vertices of the triangle are A(x1, y1), B(x2, y2), C(x3, y3), then the centroid of a triangle can be calculated by taking the average of X and Y coordinate points of all three vertices. Therefore, the centroid of a triangle can be written as:
Centroid of a triangle = ((x1+x2+x3)/3, (y1+y2+y3)/3)
|
Fig 4
Centroid Formula for Different Shapes
Here, the list of centroid formula is given for different geometrical shapes.
Shapes | Figure | x̄ | ȳ | Area |
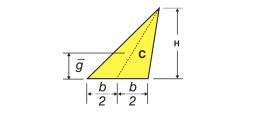
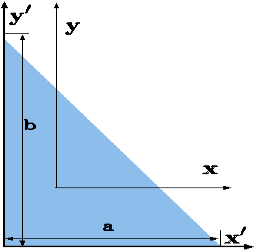
Triangular area |
| – | h/3 | bh/2 |
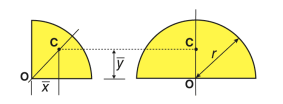
Quarter-circular area |
| 4r/3π | 4r/3π | πr2/4 |
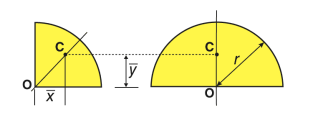
Semi-circular area |
| 0 | 4r/3π | πr2/2 |
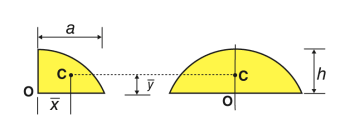
Quarter-elliptical area |
| 4a/3π | 4b/3π | πab/4 |
Semi elliptical area |
| 0 | 4b/3π | πab/2 |
Semi parabolic area |
| 3a/8 | 3h/5 | 2ah/3 |
Parabolic area |
| 0 | 3h/5 | 4ah/3 |
Parabolic spandrel |
| 3a/4 | 3h/10 | ah/3 |
Key Takeaways
1) Centroid of a triangle = ((x1+x2+x3)/3, (y1+y2+y3)/3)
2) The centroid is the centre point of the object. The point in which the three medians of the triangle intersect is known as the centroid of a triangle
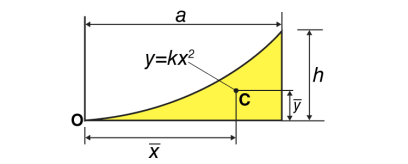
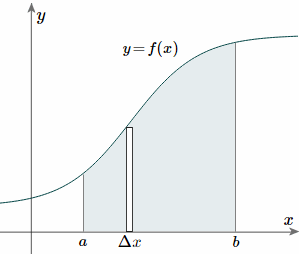
Taking the simple case first, we aim to find the centroid for the area defined by a function f(x), and the vertical lines x = a and x = b as indicated in the following figure.
|
Fig 5
To find the centroid, we use the same basic idea that we were using for the straight-sided case above. The "typical" rectangle indicated is x units from the y-axis, and it has width Δx (which becomes dx when we integrate) and height y = f(x)
Generalizing from the above rectangular areas case, we multiply these 3 values x, f(x) and Δx, which will give us the area of each thin rectangle times its distance from the x-axis), then add them. If we do this for infinitesimally small strips, we get the x-coordinates of the centroid using the total moments in the x-direction, given by:
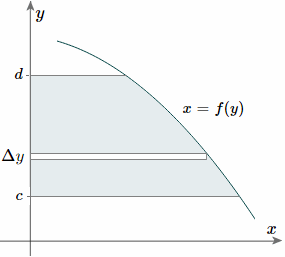
And, considering the moments in the y-direction about the x-axis and re-expressing the function in terms of y, we have:
|
Fig 6
Notice this time the integration is with respect to y, and the distance of the "typical" rectangle from the x-axis is y units. Also note the lower and upper limits of the integral are c and d, which are on the y-axis.
Of course, there may be rectangular portions we need to consider separately. (I've used a different curve for the y case for simplification.)
Alternate method: Depending on the function, it may be easier to use the following alternative formula for the y-coordinate, which is derived from considering moments in the x-direction (Note the "dx" in the integral, and the upper and lower limits are along the x-axis for this alternate method).
|
This is true since for our thin strip (width dx) the centroid will be half the distance from the top to the bottom of the strip. Another advantage of this second formula is there is no need to re-express the function in terms of y.
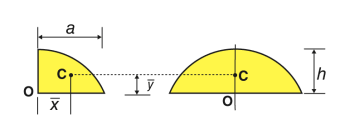
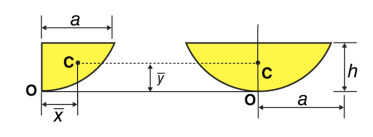
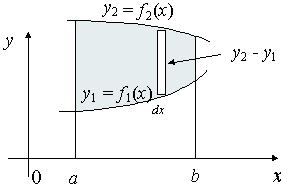
Centroids for Areas Bounded by 2 Curves
|
Fig 7
We extend the simple case given above. The "typical" rectangle indicated has width Δx and height y2 − y1, so the total moments in the x-direction over the total area is given by:
|
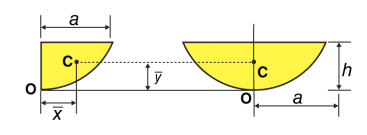
For the y coordinate, we have 2 different ways we can go about it.
Method 1: We take moments about the y-axis and so we'll need to re-express the expressions x2 and x1 as functions of y.
|
Method 2: We can also keep everything in terms of x by extending the "Alternate Method" given above:
Centroids of Composite sections ( 1D, 2D)
|
First Moments of Areas and Lines
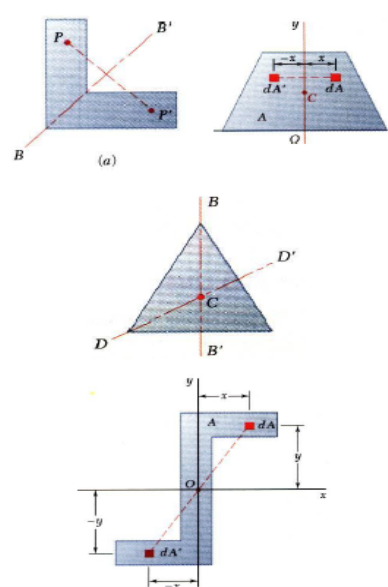
•An area is symmetric with respect to an axis BB’ if for every point P there exists a point P’ such that PP’ is perpendicular to BB’ and is divided into two equal parts by BB’.
•The first moment of an area with respect to a line of symmetry is zero.
•If an area possesses a line of symmetry, its centroid lies on that axis
•If an area possesses two lines of symmetry, its centroid lies at their intersection.
•An area is symmetric with respect to a center O if for every element dA at (x,y) there exists an area dA’ of equal area at (-x,-y).
•The centroid of the area coincides with the center of symmetry.
|
Fig 8
Key Takeaways
Centroid formula:
|
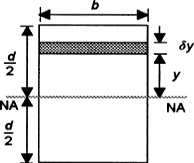
The integral ∫ y2 dA defines the second moment of area I about an axis and can be obtained by considering a segment of area δA some distance y from the neutral axis, writing down an expression for its second moment of area and then summing all such strips that make up the section concerned, i.e. integrating. As indicated in the discussion of the general bending equation, the second moment of area is needed if we are to relate the stress produced in a beam to the applied bending moment.
As an illustration of the derivation of a second moment of area from first principles, consider a rectangular cross-section of breadth b and depth d . For a layer of thickness δy a distance y from the neutral axis, which passes through the centroid, the second moment of area for the layer is:
Second moment of area of strip=y2δA=y2b δy
The total second moment of area for the section is thus:
Second moment of area=∫limits from −d/2 to d/2) y2bdy=bd3/12
|
Fig 9
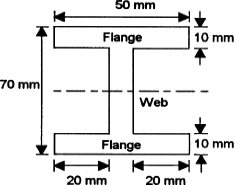
Determine the second moment of area about the neutral axis of the I-section shown in Figure 10.
|
Fig 10
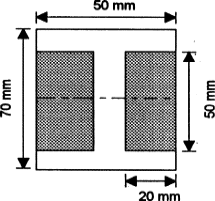
We can determine the second moment of area for such a section by determining the second moment of area for the entire rectangle containing the section and then subtracting the second moments of area for the rectangular pieces ‘missing’
|
Fig11
Thus for the rectangle containing the entire section, the second moment of area is given by I = bd3/12 = (50 × 703)/12 = 1.43 × 106mm4. Each of the ‘missing’ rectangles will have a second moment of area of (20 × 503)/12 = 0.21 × 106 mm4. Thus the second moment of area of the I-section is 1.43 × 106 − 2 × 0.21 × 106 = 1.01 × 106mm4
The product of inertia is defined as
The x and y terms inside the integral denote the centroidal position of the differential area measured from the y and x axes, respectively. Similar to moments of inertia discussed previously, the value of product of inertia depends on the position and orientation of selected axes. It is possible for the product of inertia to have a positive, negative, or even a zero value.
|
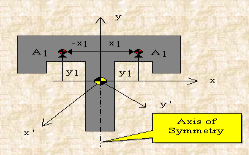
Fig 12
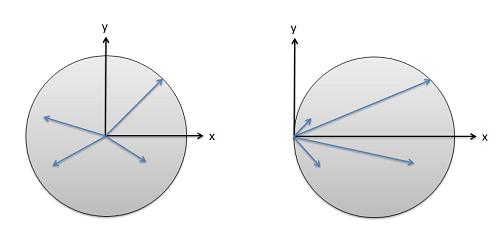
For example, either x or y represents an axis of symmetry, then the product of inertia Ixy would be zero. To see why this is the case, take a look at the figure to the right. Consider the small area A1 to the right of y axis at the distance of x1. Then consider a similar area to the left of this axis of symmetry at the distance of -x1. Since both areas are at the same vertical position from the x-axis, they have the same value of y. The contribution from the left area is -x1yA1 and that from the right is x1yA1 which add up to zero. Since every point on one side of the axis of symmetry has an equal counterpart on the other side, the total value of the integral would be zero.
However, if we were to consider the product of inertia with respect to the x' and y' axes, then Ix'y' would not be zero. We will have more discussion about the product of inertia in the section on principal axes.
For a general three-dimensional body, it is always possible to find 3 mutually orthogonal axes (an x, y, z coordinate system) for which the products of inertia are zero, and the inertia matrix takes a diagonal form. In most problems, this would be the preferred system in which to formulate a problem. For a rotation about only one of these axis, the angular momentum vector is parallel to the angular velocity vector. For symmetric bodies, it may be obvious which axis is principle axis. However, for an irregular-shaped body this coordinate system may be difficult to determine by inspection; we will present a general method to determine these axes in the next section. But, if the body has symmetries with respect to some of the axis, then some of the products of inertia become zero and we can identify the principal axes.
For instance, if the body is symmetric with respect to the plane  then, we will have
then, we will have 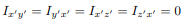 and
and 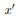 will be a principal axis. This can be shown by looking at the definition of the products of inertia.
will be a principal axis. This can be shown by looking at the definition of the products of inertia.
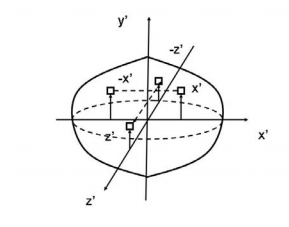
|
Fig 13
The integral for, say,  can be decomposed into two integrals for the two halves of the body at either side of the plane
can be decomposed into two integrals for the two halves of the body at either side of the plane . The integrand on one half
. The integrand on one half 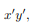 will be equal in magnitude and opposite in sign to the integrand on the other half (because
will be equal in magnitude and opposite in sign to the integrand on the other half (because 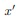 will change sign). Therefore, the integrals over the two halves will cancel each other and the product of inertia
will change sign). Therefore, the integrals over the two halves will cancel each other and the product of inertia 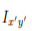 will be zero. (As will the product of inertia
will be zero. (As will the product of inertia 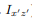 ) Also, if the body is symmetric with respect to two planes passing through the center of mass which are orthogonal to the coordinate axis, then the tensor of inertia is diagonal, with
) Also, if the body is symmetric with respect to two planes passing through the center of mass which are orthogonal to the coordinate axis, then the tensor of inertia is diagonal, with 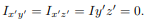
|
Fig 14
Another case of practical importance is when we consider axisymmetric bodies of revolution. In this case, if one of the axes coincides with the axis of symmetry, the tensor of inertia has a simple diagonal form. For an axisymmetric body, the moments of inertia about the two axis in the plane will be equal. Therefore, the moment about any axis in this plane is equal to one of these. And therefore, any axis in the plane is a principal axis. One can extend this to show that if the moment of inertia is equal about two axis in the plane (IP P = Ixx), whether or not they are orthogonal, then all axes in the plane are principal axes and the moment of inertia is the same about all of them. In its inertial properties, the body behaves like a circular cylinder.
|
Fig 15
The tensor of inertia will take different forms when expressed in different axes. When the axes are such that the tensor of inertia is diagonal, then these axes are called the principal axes of inertia.
Key takeaways
1) Second moment of area of strip=y2δA=y2b δy
2) Thus for the rectangle containing the entire section, the second moment of area is given by I = bd3/12
The Transfer theorem is also known as Parallel Axis Theorem.
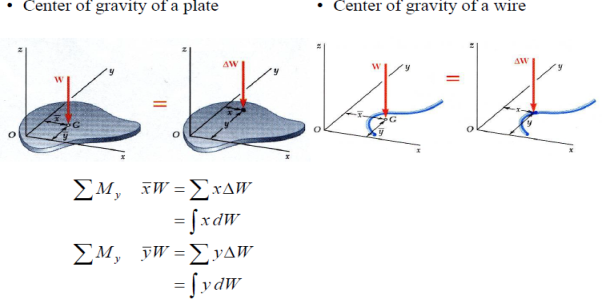
When we calculated the area and mass moments of inertia via integration, one of the first things we had to do was to select a point or axis we were going to take the moment of inertia about. We then measured all distances from that point or axis, where the distances were the moment arms in our moment integrals. Because the centroid of a shape is the geometric center of an area or volume, the average distance to any one point in a body is at a minimum.
If we pick a different point or axis to take the moment of inertia about then on average all the distances in our moment integral will be a little bit bigger Specifically the further we move from the centroid, the larger the average distances become.
|
Fig 16 The distance used in our moment integrals depends on the point or axis chosen. These distances will be at a minimum at the centroid and will get larger as we start further from the centroid.
Though this complicates our analysis, the nice thing is that the change in the moment of inertia is predicable. It will always be at a minimum when we take the moment of inertia about the centroid, or an axis going through the centroid. This minimum, which we will call Ic is the value we will look up in our moment of inertia table. From this minimum, or unadjusted value, we can find the moment of inertia value about any point Ip by adding an an adjustment factor equal to the area times distance squared for area moments of inertia, or mass times distance squared for mass moments of inertia.
IxxP=IxxC+A∗r2
IxxP=IxxC+m∗r2
This adjustment process with the equations above is the parallel axis theorem. The area or mass terms simply represent the area or mass of the part you are looking at, while the distance (r) represents the distance we are moving the axis we are taking the moment of inertia about. This may be a vertical distance, a horizontal distance, or a diagonal depending on the axis the moment or inertia is about.
|
Fig 17 The distance (r) in the Parallel Axis Theorem represents the distance we are moving the axis we are taking the moment or intent about.
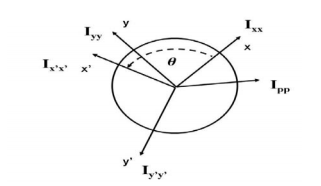
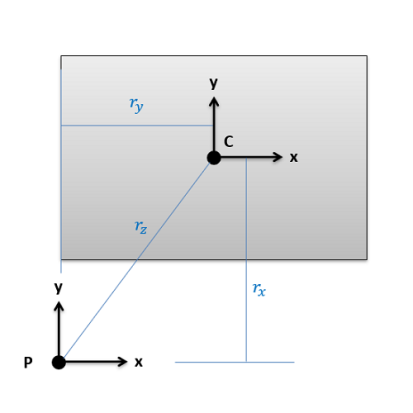
Say we are trying to find the moments of inertia of the rectangle above about point P. We would start by looking up Ixx, Iyy, and Jzz about the centroid of the rectangle (C) in the moment of inertia table. Then we would add on an area times distance squared term to each to find the adjusted moments of inertia about P. The distance we are moving the x axis for Ixx is the vertical distance rx, the distance we are moving the y axis for Iyy is the horizontal distance ry, and the distance we would move the z axis (which is pointing out of the page) for Jzz is the diagonal rz. Center of mass adjustments follow a similar logic, using mass times distance squared, where the distance represents how far you are moving the axis of rotation in three dimensional Spaces
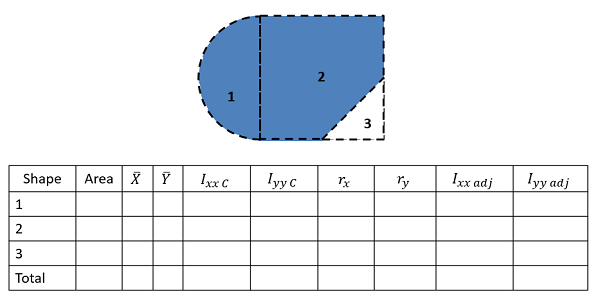
Using the Method of Composite Parts to Find the Moment of Inertia
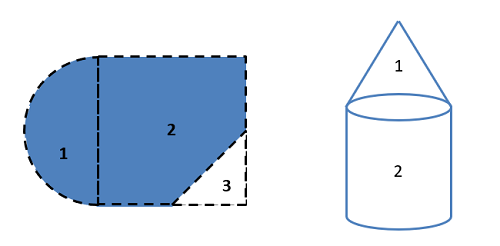
To find the moment of inertia of a body using the method of composite parts, you need to start by breaking your area or volume down into simple shapes. Make sure each individual shape is available in the moment of inertia table, and you can treat holes or cut-out’s as negative area or mass.
|
Fig 18 Start by breaking down your area or volume into simple parts and number those shapes. Holes or cut-outs will count as negative areas or masses.
Next you are going to create a table to keep track of values. Devote a row to each part that your numbered earlier, and include a final "total" row that will be used for some values. Most of the work of the method of composite parts is filling in this table The columns will vary slightly with what you are looking for, but you will generally need the following.
|
Fig 19 most work in the method of composite parts will revolve around filling out a table such as this one. This table contains the rows and columns necessary to find the rectangular area moments of inertia (Ixx and Iyy) for this composite body.
- The area or mass for each piece (area for area moments of inertia or mass for mass moments of inertia). Remember cut outs should be listed as negative areas or masses.
- The centroid or center of mass locations (X, Y and possibly Z coordinates). Most of the time, we will be finding the moment of inertia about centroid of the composite shape, and if that is not explicitly given to you, you will need to find that before going further. For more details on this, see the page "Centroids and Center of Mass via Method of Composite Parts".
- The moment of inertia values about each shape's centroid. To find these values you will plug numbers for height, radius, mass, etc. into formulas on the moment of inertia table. Do not use these formulas blindly though as you may need to mentally rotate the body, and thus switch equations, if the orientation of the shape in the table does not match the orientation of the shape in your diagram.
- The adjustment distances (r) for each shape. For this value you will want to determine how far the x-axis, y-axis, or z-axis moves to go from the centroid of the piece to the overall centroid, or point you are taking the moment of inertia about. To calculate these values generally, you will be finding the horizontal, vertical, or diagonal distances between piece centroids and the overall centroids that you have listed earlier in the table. See the parallel axis theorem section of this page earlier for more details.
- Finally, you will have a column of the adjusted moments of inertia. Take the original moment of inertia about the centroid, then simply add your area times r squared term or mass times r squared term for this adjusted value.
The overall moment of inertia of your composite body is simply the sum of all of the adjusted moments of inertia for the pieces, which will be the sum of the values in the last column (or columns if you are finding the moments of inertia about more than one axis).
Product of inertia
In addition to the moment of inertia, the product of inertia is commonly used. Here only the product of the area is defined and discussed. The product of inertia defined as
Ixixj=∫A xixjdA
For example, the product of inertia for xx and yy axes is
Ixy=∫AxydA
Product of inertia can be positive or negative value as oppose the moment of inertia. The calculation of the product of inertia isn't different much for the calculation of the moment of inertia. The units of the product of inertia are the same as for moment of inertia.
Same as for moment of inertia there is also similar theorem.
I x′y′ = ∫A x′y′dA = ∫A(x+Δx)(y+Δy)dA
Expanding equation above results in
I x′y′ = ∫AxydA+ ∫AxΔydA + ∫AΔxydA + ∫AΔxΔydA
The final form is
I x′y′ = Ixy + ΔxΔydA
There are several relationships should be mentioned
I xy =I yx
Symmetrical area has zero product of inertia because integration of odd function (asymmmertial function) left part cancel the right part.
|
Fig. 20 Product of inertia
The principle of virtual work was proposed by the Swiss mathematician Jean Bernoulli in the eighteenth century. It provides an alternative method for solving problems involving the equilibrium of a particle, a rigid body, or a system of connected rigid bodies.
The definitions of the work of a force and a couple can be presented in terms of the actual movements which are expressed by differential displacements having values of 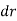 and
and 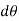 . Consider now an imaginary or virtual movement of a body in static equilibrium, which indicates a displacement or rotation that is assumed and does not actually exist. These movements are first-order differential quantities and will be denoted by the symbols
. Consider now an imaginary or virtual movement of a body in static equilibrium, which indicates a displacement or rotation that is assumed and does not actually exist. These movements are first-order differential quantities and will be denoted by the symbols 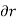 and
and 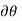 (delta r and delta
(delta r and delta 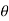 ), respectively. The virtual work done by a force having a virtual displacement
), respectively. The virtual work done by a force having a virtual displacement 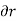 is
is
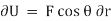
Similarly, when a couple undergoes a virtual rotation 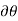 in the plane of the couple forces, the virtual work is
in the plane of the couple forces, the virtual work is

According to the principle of virtual work if a body is in equilibrium, then virtual displacement of the body is zero for all the algebraic sum of the virtual work which is done by all the forces and moments of couple that are acting on the body. Thus,
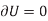
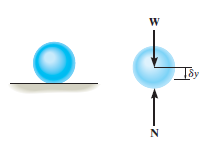
For example, consider the free-body diagram of the particle (ball) that rests on the floor, Fig. below. If we “imagine” the ball to be displaced downwards a virtual amount 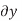 then the weight does positive virtual work
then the weight does positive virtual work 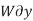 , and the normal force does negative virtual work
, and the normal force does negative virtual work 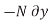 , For equilibrium the total virtual work must be zero, so that
, For equilibrium the total virtual work must be zero, so that
|
Fig 21
As seen from the above example, no added advantage is gained by solving particle and rigid-body equilibrium problems using the principle of virtual work. This is because for each application of the virtual-work equation, the virtual displacement, common to every term, factors out, leaving an equation that could have been obtained in a more direct manner by simply applying an equation of equilibrium.
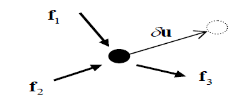
A particle of mass m is acted upon by a number of forces f1,f2….fN Suppose the particle undergoes a virtual displacement 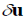 to reiterate, these impressed forces fi do not cause the particle to move, one imagines it to be incorrectly positioned a little away from the true equilibrium position.
to reiterate, these impressed forces fi do not cause the particle to move, one imagines it to be incorrectly positioned a little away from the true equilibrium position.
|
Fig 22
If the particle is moving with an acceleration a, the quantity -ma is treated as an inertial force. The total virtual work is then (each term here is the dot product of two vectors)
|
Now if the particle is in equilibrium by the action of the effective (impressed plus inertial) force then 
This can be expressed as follows:
The principle of virtual work (or principle of virtual displacements) if a particle is in equilibrium under the action of a number of forces (including the inertial force) the total work done by the forces for a virtual displacement is zero.
Alternatively, one can define the external virtual work  Wext and the virtual kinetic energy
Wext and the virtual kinetic energy 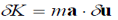 in which case the principle takes the form
in which case the principle takes the form 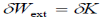 (compare with the work-energy principle
(compare with the work-energy principle
In the above, the principle of virtual work was derived using Newton’s second law. One could just as well regard the principle of virtual work as the fundamental principle and from it derive the conditions for equilibrium. In this case one can say that The principle of virtual work (or principle of virtual displacements)
a particle is in equilibrium under the action of a system of forces (including the inertial force) if the total work done by the forces is zero for any virtual displacement of the particle. The term kinematically admissible displacement is used to mean one that does not violate the constraints, and hence one arrives at the version of the principle which is often used in practice:
The principle of virtual work (or principle of virtual displacements):a particle is in equilibrium under the action of a system of forces (including the inertial force) if the total work done by the forces (excluding reaction forces) is zero for any kinematic ally admissible virtual displacement of the particle.
Key takeaways
1) The virtual work done by a force having a virtual displacement 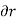 is
is
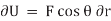
Beam –
It is horizontal structural member on which different types of loads can be supported. It takes load from floor or roof & transfers to column.
The beam may be sometimes constructed in the inclined position for architectural point of view.
Types of Beam: -
- Simply supported beam –
A beam which is just resting on the supports at the end without any connection is known as simply supported beam. It is generally used for vertical landing system.
|
Fig 23
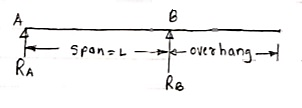
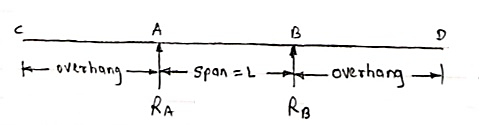
2. Overhanging Beam –
A beam which is supported at the intermediate point other than ends is called as overhanging beam. Here portion of beam is extended beyond the support
(singly overhanging beam)
b)
(doubly overhanging beam)
|
Fig 24
3. Cantilever Beam –
A beam which is fixed at one end is called as cantilever beam
|
Fig 25
Here, there are three reactions components:
- Vertical reaction at A (RVA)
- Horizontal reaction at A (RHA)
- Fixing moment at A (MA)
We can assume any direction for above components.
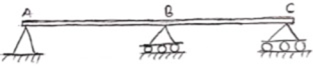
4. Continuous Beam:
A beam having more than two supports is called as continuous beam.
|
Fig 26
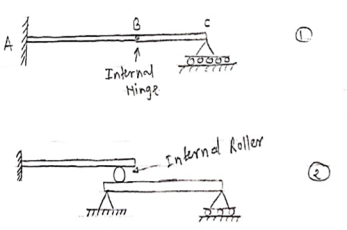
5. Compound Beam:
When two or more beams are joined together by using internal hinge; or when one beam rests over another beam by using internal roller, then such beam is called as compound beam.
|
Fig 27
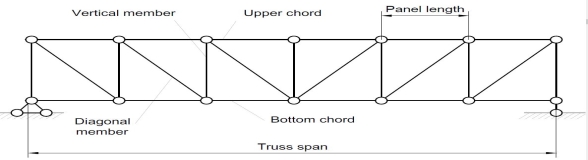
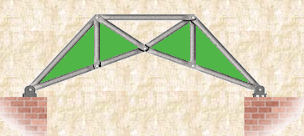
Trusses are simply defined as triangulation of members to make the stabilized structure. Triangulation is the stable configuration mathematically. Generally, a truss has the members called as top chord, bottom chord, vertical chord and diagonal chord. The main functions of the trusses are:
- Carrying the loads from the over structures
- Providing adequate lateral stability to the entire structure
|
Fig 28
There are some basic assumptions in the designing process. It should be clarified that the construction of the trusses should conform with the design assumptions to avoid the unwanted failures due to the dispersion of the forces and loads.
Following are the assumptions in truss design.
- Truss members will carry only the axial forces
- The nodes i.e. the connections of the members are designed as pinned joints so that moments won’t be transferred to the members of the truss
- All the external loads and the reactions are act only on the nodes
- Generally, the truss should be in a plane.
- Typically the members of the trusses are made as I sections, angles, T sections, Tube sections, Square sections and channel sections. I sections are more preferable as an optimized section in terms of the structural forces.
- Simple truss – indicates a single triangular truss. These trusses are most often used as the roof trusses.
- Planar truss – as the name implies it is a two dimensional truss. If all the members and the nodes are in a planar surface, then this truss is a planar truss.
- Space frame truss – Contrast to planar truss, the members and the nodes are located in the three dimensional space. Electrical and telecom towers are the one of the simplest example that we are seeing in the day to day life.
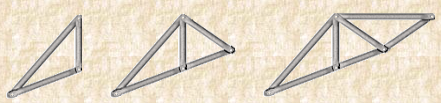
Simple Truss: It is possible to create a simple truss by joining three bars together to form a triangle. We can increase the size of the truss by adding two more members with an additional joint. By repeating this process, we can develop simple trusses with different shapes as shown below. The triangular building block assures internal stability of the truss structure as it is increased in size.
|
Fig 29
Although it is possible to have non-triangular cells in a simple truss, internal stability will not be guaranteed in that case.
Compound Truss: A compound truss is made up of simple trusses joined together to form a larger truss. The figure below shows a compound truss consisting of two simple trusses joined by a common joint and a bar. It is also possible to have multiple simple trusses joined together to create a larger compound truss. The connection of simple trusses then becomes a design issue determined based on the size of the resulting compound truss. Compound trusses are commonly used to support loads over long spans as in bridges.
|
Fig 30
Complex Truss: A complex truss uses a general layout of members different from that used in simple and compound trusses. It often incorporates overlapping members.
|
Fig 31
Key takeaways
1) Simple truss – indicates a single triangular truss. These trusses are most often used as the roof trusses.
2) Planar truss – as the name implies it is a two dimensional truss. If all the members and the nodes are in a planar surface, then this truss is a planar truss
Reference:
1. Engineering Mechanics: F. L. Singer
2. Engineering Mechanics: Timoshenko & Young
3. Engineering Mechanics: Bear & Johnston
4. Engineering Mechanics: I. H. Shames
5. Engineering Mechanics: A. Nelson