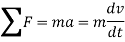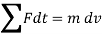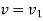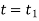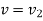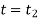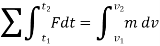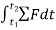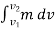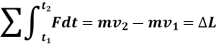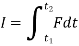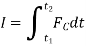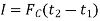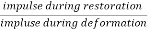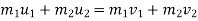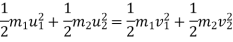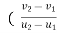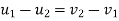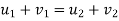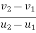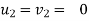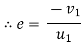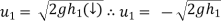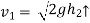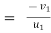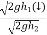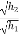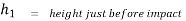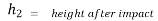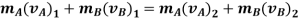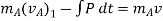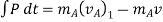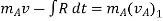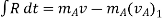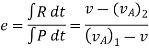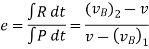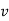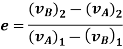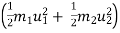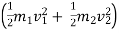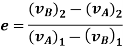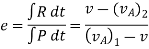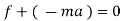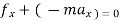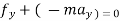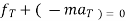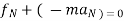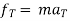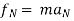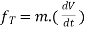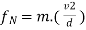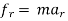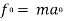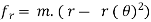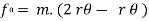UNIT-5
Collision of elastic bodies
The principle of energy conservation states that energy is neither created nor destroyed. It may transform from one type to another. Like the mass conservation principle, the validity of the conservation of energy relies on experimental observations; thus, it is an empirical law. No experiment has violated the principle of energy conservation yet. The common forms of energy include thermal, electrical, chemical, mechanical, kinetic, and potential. It may also be stated that the sum of all kinds of energy is constant.
∑Ek=constant
Where E denotes energy and subscript k refers to the different types of energy.
Many engineering applications involve transformation of energy between two or three types only. For instance, in dynamics problems, the conservation of energy accounts for two types of energy, i.e., kinetic and potential (in some cases frictional work), neglecting the effect of other forms like chemical, thermal, or electrical. In chemical reactions, the conservation of energy includes thermal and chemical energies, and the effect of other forms of energy is ignored. In most thermodynamic problems, the principle of energy conservation applied to nonreactive systems accounts for thermal and mechanical energies.
Law of Conservation of Energy Derivation
Considering the potential energy at the surface of the earth to be zero Let us see an example of a fruit falling from a tree.
Consider a point A, which is at height ‘H’ from the ground on the tree, the velocity of the fruit is zero hence potential energy is maximum there.
E = mgH ———- (1)
When the fruit is falling, its potential energy is decreasing and kinetic energy is increasing.
At point B, which is near the bottom of the tree, the fruit is falling freely under gravity and is at a height X from the ground, and it has speed as it reaches point B. So, at this point, it will have both kinetic and potential energy.
E = K.E + P.E
P.E = mgX ——— (2)
According to third equation of motion,
v2=2g (H–X)
1/ 2mv2=1/2 m.2g (H–X)
K.E=1/2 m.2g (H–X)
K.E=mg (H–X)
K.E=mg (H-X)——– (3)
Using (1) (2) and (3)
E = mg (H – X) + mgX
E = mg (H – X + X)
E = mgH
Similarly, if we see the energy at point C, which is at the bottom of the tree, it will come out to be mgH. We can see as the fruit is falling to the bottom and here, potential energy is getting converted into kinetic energy. So there must be a point where kinetic energy becomes equal to potential energy. Suppose we need to find that height ‘x’ from the ground. We know at that point,
K.E = P.E
P.E = K.E = E/2 ——– (4)
E2 is the new energy
Where, E = mgH2
H2 is the new height.
As the body is at height X from the ground,
P.E = mgX ——— (5)
Using (4) and (5) we get,
mgX = mgH / 2
X=H/2
H2 is referred to the new height
Law of Conservation of Energy Examples:
In Physics, most of the inventions rely on the fact that energy is conserved when it is transferred from one form to another. A number of electrical and mechanical devices operate solely on the law of conservation of energy. We will discuss a few examples here.
- In a torch, the chemical energy of the batteries is converted into electrical energy, which is converted into light and heat energy.
- In hydroelectric power plants, waterfalls on the turbines from a height. This, in turn, rotates the turbines and generates electricity. Hence, the potential energy of water is converted into the kinetic energy of the turbine, which is further converted into electrical energy.
- In a loudspeaker, electrical energy is converted into sound energy.
- In a microphone, sound energy is converted into electrical energy.
- In a generator, mechanical energy is converted into electrical energy.
- When fuels are burnt, chemical energy is converted into heat and light energy.
- Chemical energy from food is converted to thermal energy when it is broken down in the body and is used to keep it warm.
Key takeaways
1) When the fruit is falling, its potential energy is decreasing and kinetic energy is increasing
2) In a torch, the chemical energy of the batteries is converted into electrical energy, which is converted into light and heat energy.
Using kinematics, the equation of motion for a particle of m is given by,
Integrating above equation between limits
The term Since m is a positive scalar, the linear-momentum vector has the same direction as v. Linear impulse is a vector quantity that measures the effect of a force during the time the force acts. As time is a positive scalar quantity, the impulse acts in the same direction as the force. If the force is variable, the resulting impulse is given by
If the force is constant in magnitude and also in direction, the resulting impulse is given by
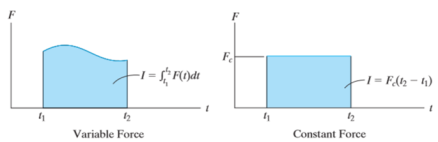
Graphically, magnitude of linear impulse is given by the area under the curve plotted on the force versus time plot.
Fig 1
|
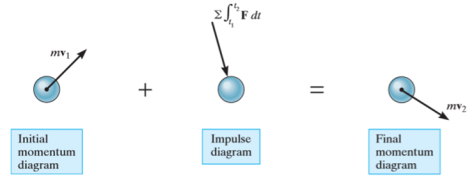
Principle of impulse momentum states that sum of all the impulses applied to the particle in a time period of motion of a particle is equal to the change in momentum of the particle.
Mathematically,
Initial momentum + sum of impulses = Final momentum
|
Fig 2
Work energy equation
The principle of work and kinetic energy (also known as the work-energy theorem) states that the work done by the sum of all forces acting on a particle equals the change in the kinetic energy of the particle. This definition can be extended to rigid bodies by defining the work of the torque and rotational kinetic energy.
|
Fig 3
Kinetic Energy: A force does work on the block. The kinetic energy of the block increases as a result by the amount of work. This relationship is generalized in the work-energy theorem.
The work W done by the net force on a particle equals the change in the particle’s kinetic energy KE:
W=ΔKE=1/ 2 mv2f−1/ 2mv2i
Where vi and vf are the speeds of the particle before and after the application of force, and m is the particle’s mass.
For the sake of simplicity, we will consider the case in which the resultant force F is constant in both magnitude and direction and is parallel to the velocity of the particle. The particle is moving with constant acceleration a along a straight line. The relationship between the net force and the acceleration is given by the equation F = ma (Newton’s second law), and the particle’s displacement d, can be determined from the equation
v2f=v2i+2ad
Obtaining
d=v2f−v2i / 2a
The work of the net force is calculated as the product of its magnitude (F=ma) and the particle’s displacement. Substituting the above equations yields:
W=F x d
=ma (v2f−v2i)/2a
=1/2mv2f −1/2mv2i
=KEf − KEi =ΔKE
Key takeaways
1) The equation of motion for a particle of m is given by,
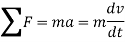
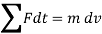
2) The work W done by the net force on a particle equals the change in the particle’s kinetic energy KE:
W=ΔKE=1/ 2 mv2f−1/ 2mv2i
Coefficient of Restitution (e)
It is the ratio of impulses during the restoration period and deformation period .it is denoting by e.
This is always positive and lies between o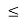 e
e 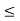 1.
1.
e =
|
When the impact takes place , the two object initially goes under the deformation for small duration & then , they tries to region their original shape , size
1] Perfectly elastic impact:-
In this impact, both bodies regain their shapes & size completely
I.e. there is complete restoration here
a] momentum is conserved along the line of impact
b] K.E. is also conserved .no loss of K.E. during impact
c] Coefficient of restitution (e) = 1 e= 1=
|
d] Both bodies separates after imput.
2] Perfectly plastic impact:-
In this impact both bodies are couple together after the impact and they move together with same velocity, here permanent deformation take place . so there is no restitution.
a] Here , momentum is conserved :-
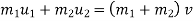
 Where
Where
V = common velocity of both bodies after Impact
.
b] K.E.is not conserved .there is loss of k.e. during impact.
Loss of K.E. = total k.e. before impact – total k. e. after impact
Loss of K.E. = 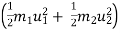 -
- 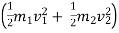
c] Both bodied move together after impact.
d] Coefficient of restitution (e) = 0
3) Partially elastic (semi elastic) impact
In this impact, both bodies do not regain their original shape & size completely. But there is a partial restoration.
a) Here momentum is conserved.
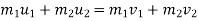
b) K.E. is not conserved .there is some loss in K.E
Initial K.E. > KE after impact
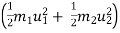 >
>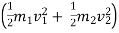
c] Coefficient of restitution is more than zero & less than 1
0 < e < 1
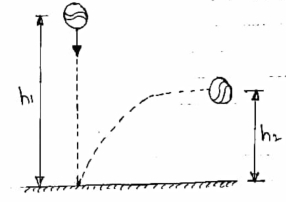
4) Impact with very large mass (infinite mass)
When a body of small collides with a body of very large mass as compared to first body, then the impact is considered as impact with infinite mass.
Ex .a ball is dropped on the floor
|
Fig 4
a) in this type of impact, low of conservation of momentum cannot be applied .
b] There is no loss I KE due to impact
c] Coefficient of restitution is
e = But velocity if floor before & after impact is zero.
Velocity of ball just before the impact when it is dropped frm height h1 is ,
After the impact ball rises to the height h2 then its velocity after the impact is e where
|
Impact of elastic bodies
Impact occurs when two bodies collide with each other in a very short period of time, resulting relatively huge (impulsive) forces to be exerted between the bodies.
Example: striking of a hammer on a nail, a golf club on a ball
There are two types on impact:
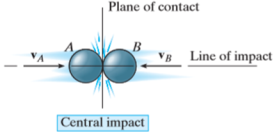
- Central Impact
Central impact occurs when the direction of motion of the mass centres of the two colliding particles is along a line passing through the mass centres of the particles. This line is called the line of impact which is perpendicular to plane of contact.
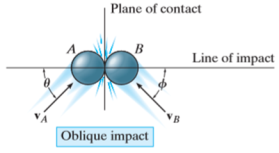
2. Oblique impact
When the motion of one or both of the particles make an angle with the line of impact, then the impact is said to be oblique impact
|
Fig 5
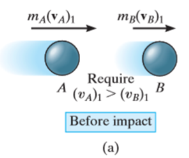
Consider two particles A and B involving the central impact of the shown in Fig. a
|
Fig 6
Let velocity of particle A is more than particle B.
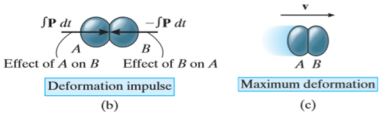
During the collision the particles must be considered as deformable or no rigid particles. The particles will undergo a period of deformation such that they exert an equal but opposite deformation impulse 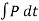 on each other.
on each other.
When the deformation becomes maximum the relative motion of particle will become zero. Hence, the particle will move with same velocity v.
|
Fig 7
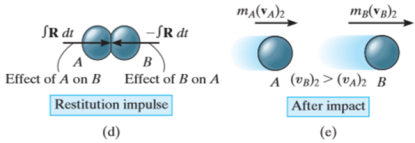
Then the particles will either return to their original shape or remain permanently deformed. This occurs after the period of restitution.
The equal but opposite restitution impulse 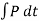 pushes the particles apart from each another, shown in fig d. In reality, the physical properties of any two bodies are such that the deformation impulse will always be greater than that of restitution.
pushes the particles apart from each another, shown in fig d. In reality, the physical properties of any two bodies are such that the deformation impulse will always be greater than that of restitution.
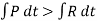
After the separation, the particles will have the final momenta as shown in Fig e.
|
Fig 8
Momentum for the system of particles is conserved as during the collision the internal impulses of deformation and restitution cancel each other.
Hence,
Applying impulse momentum equation for particle A during deformation phase (fig a, b and c), we get
Now, applying impulse momentum equation for particle A during restitution phase (fig c, d and e), we get
The ratio of the restitution impulse to the deformation impulse is called the coefficient of restitution.
Similarly, Coefficient of restitution can be established for particle B.
If velocity
|
When, e = 1, the collision between the two particles is perfectly elastic. In perfectly elastic collision, the deformation impulse is equal and opposite to the restitution impulse. This is the ideal case and is impossible to achieve this case.
When e = 0, the collision between the two particles is perfectly plastic. In this case there is no restitution impulse so that after collision both particles couple or stick together and move with a common velocity.
Key takeaways
1) K.E.is not conserved. there is loss of k.e. during impact. 2) Loss of K.E. = total k.e. before impact – total k. e. after impact 3) Loss of K.E. = 4) Coefficient of restitution can be expressed in terms of the particle’s initial and final velocities
5) The ratio of the restitution impulse to the deformation impulse is called the coefficient of restitution.
|
D’Alembert’s principle
It states that the sum of external force acting on a body and inertia force is always equal to zero.
∑
∑
2. For universal motion ∑ ∑
|
D’-ALMBERTS Principle for universal motion :-
D’-ALMBERTS Principle for universal motion in Cartesian coordinates:-
∑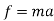
∑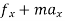
∑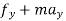
∑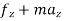
D’-ALMBERTS principle for curvilinear motion in path variables (tangential and normal coordinates) :-
∑ ∑ For radial and transverse coordinates :- ∑ Therefore, ∑
|
Reference:
1. Engineering Mechanics: F. L. Singer
2. Engineering Mechanics: Timoshenko & Young
3. Engineering Mechanics: Bear & Johnston
4. Engineering Mechanics: I. H. Shames
5. Engineering Mechanics: A. Nelson