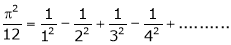Unit – 3
Fourier series
Content
3.1 Fourier series of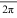 
periodic function
3.1 Fourier series of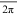 
periodic function
Periodic functios- if the value of the function( y-axis) repeats itself on x-axis, then the function is called periodic function.
Suppose f(x) is a function , then
If f(x) = f(x + t) = f( x + 2t) = …………….
Then t is called the periodic of the function f(x).
Suppose of we take sin x , then it repeats its value after the period of 2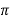
such that, we write this as
Sin x = sin ( x + 2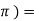
sin ( x + 4
) ………….
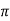We can say that sin x is a periodic function with the period of 2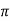
First we will define the Fourier series-
A series of the form,
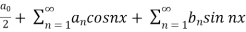
Is called fourier series , where
are constants.
Any periodic function can be expanded in the form of fourier series.
Determination of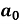 
, 
, 
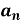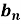of Fourier series-
We know that, the fourier series,
f(x) =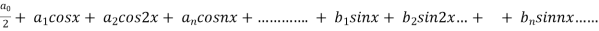 
------------ eq.(1)
To find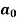 
–
Intergrate equation (1) on both sides, from 0 to 2π
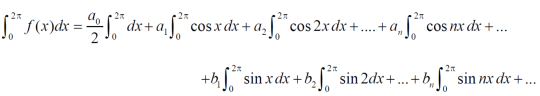
Which gives,
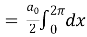
To find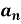 
-
Multiply each side of eq. (1) by cos nx and integrate from 0 to 2π
We get,
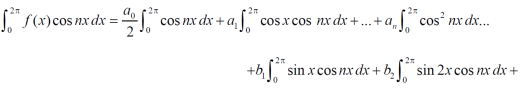
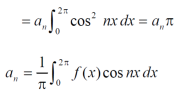
Similarly we can find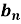 
by , multiplying eq. (1) by sin nx and integrating from 0 to 2π
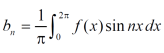
Example: Find the fourier series of the function f(x) = x where 0 < x < 2 π
Sol. We know that, from fourier series,
f(x) =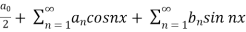 
First we will find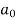 
,
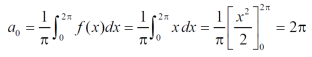
Now,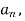 
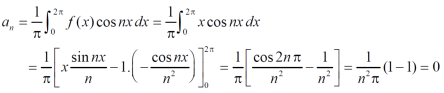
And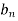 
,
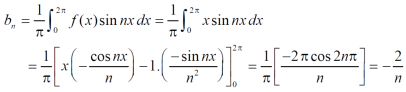
Put these value in fourier series, we get
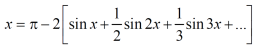
Example: Find the fourier series for f(x) = x / 2 over the interval 0 < x < 2π
And has period 2π
Sol. First we will find
= 
= 
=
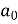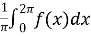
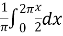
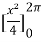
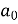= π
= π
Similarly,
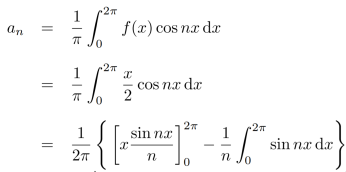
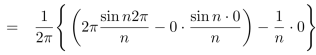
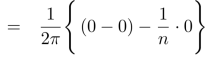
Which gives,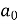 
= 0
Now,
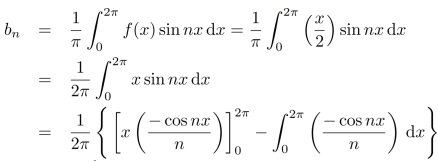
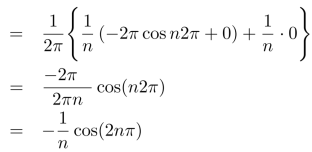
We get,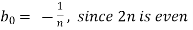 
We know that, the fourier series
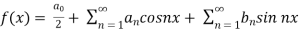
Put these values in fourier series, we get
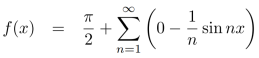
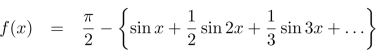
Let f(x) be a function defined in C < x < C + 2L such that
1) f(x) is defined and single valued in the given internal also.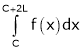 
exist.
2) f(x) may have finite number of finite discontinuities in the interval.
3) f(x) may have finite number of maxima or minima in the given interval.
As we know that the Fourier series is an expansion of periodic function f(x).
We can say that it is the expansion of the infinite sum of sines and cosines.
Fourier series make the orthogonality relationship of sin and cosine functions.
Orthogonality of the trigonometric functions-
1. Suppose there are two functions f and g , then the inner product of f and g on [a,b] is
< f , g> =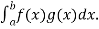 
2. f and g are orthogonal on [a,b] is <f,g> = 0.
The series of the functions
, 
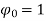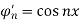and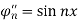 
for all n>=0
Are orthogonal on [ -p , p] , the associate orthogonal series expansion of a function f is,
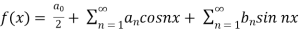
Definition:
Fourier Series
Let f(x) be a periodic function of period 2L. Defined in the internal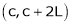 
and satisfied Dirichlet's conditions, then f(x) can be expressed as,
.
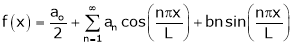Where ao, an, bn are called Fourier constant’s or Fourier coefficients and are given by,
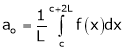
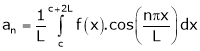
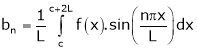
Note:
That there are only 4 intervals as below. i.e.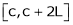 
is divided into following four intervals.
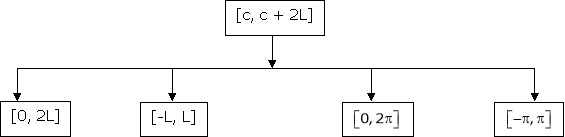
Note that for [0, 2L] we put c = 0
Hence Fourier series in this interval will be,
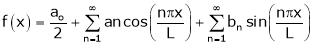
Where
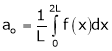
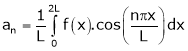
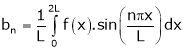
Simillarly, for the interval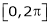 
we put c = 0,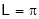 
Hence Fourier series in this interval will be
Where
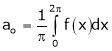
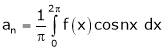
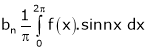
Note that for the interval [-L, L] i.e. put C = -L,
First we check whether f(x) is even function or odd.
Case I:-
If f(x) is even function. Then we get half range cosine series as,
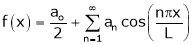
Where
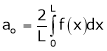
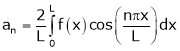
Case II:-
If f(x) is odd function. Then we get half range sine series as,
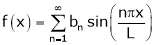
Where
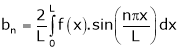
Simillarly
Note that for that interval 
i.e. put 
, 
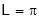
First we check wheatear f(x) is even or odd function.
Case I:-
If f(x) is even function then we get half range cosine series as
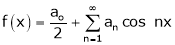
Where
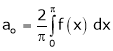
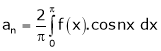
Case II:-
If f(x) is odd function then we get half range sine series as,
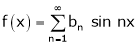
Where
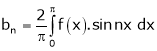
Note that
- For half range cosine series i.e. f(x) is even function bn = 0
- For half range sine series i.e. f(x) is odd function ao = an = 0
Exercise
Find the Fourier series of f(x) = x in the interval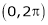 
Solution:
Here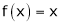 
; 
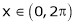
It’s Fourier series is given by
… (1)
Where
&
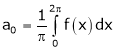
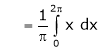
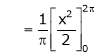
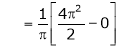
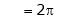
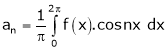
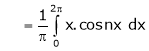
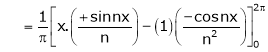
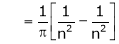
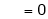
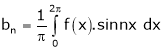
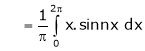
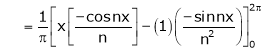
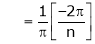
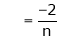
Hence the required Fourier series is
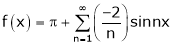
- Find the Fourier series for
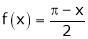in the interval 
Hence deduce that
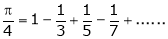
Solution:
Here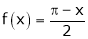 
; 
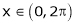
Hence it’s Fourier series is,
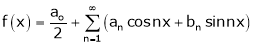… (1)
Where
&
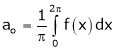
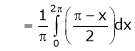
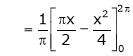
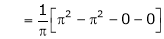
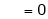
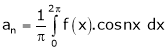
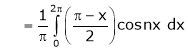
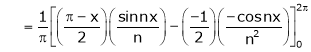
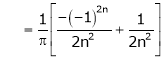
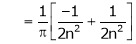
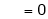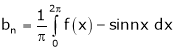
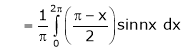
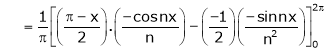
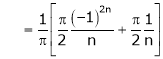
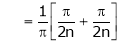
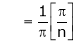
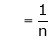
Hence equation (1) becomes
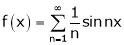
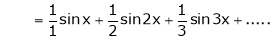
Put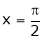 
we get
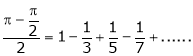
i.e.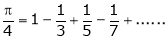 
2. Find a Fourier series expansion in the interval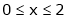 
for
; 
; 
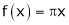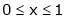
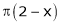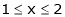
Solution:
Here
; 
; 
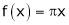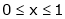
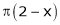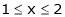
Hence it’s Fourier series expansion is,
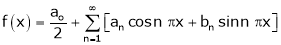… (1)
Where
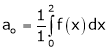
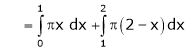
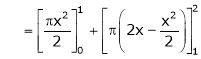
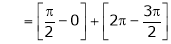
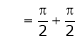
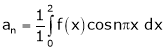
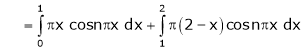
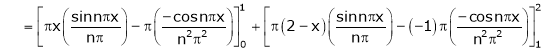
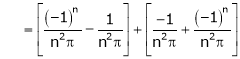
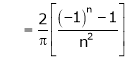
And
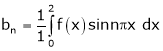
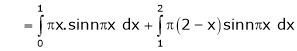
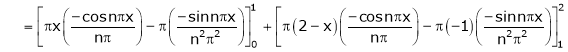
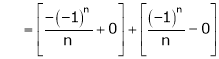
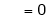
Hence equation (1) becomes
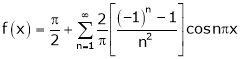
3. Find a Fourier series of
; 
; 
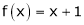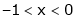
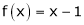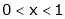
Solution:
Here
; 
; 
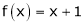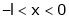
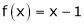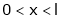
Here f(x) is odd function Hence we get half range sine series i.e.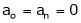 
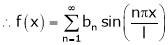… (1)
Where
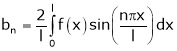
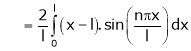
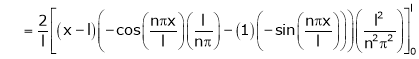
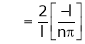
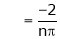
Hence equation (1) becomes,
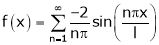
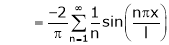
Odd function-
A function f(x), which is written as ,
f( - x ) = - f(x)
Is known as odd function.
The graph of the odd function looks like-
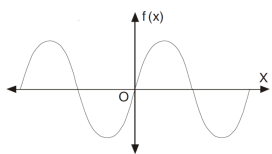
Tha graph of the function is symmetric about x-axis.
And the area under the curve from -π to π is always zero.(see fig)
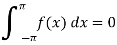
Even function-
If f(-x) = f(x) then the function is known as even function.
The graph of the function f(x) looks like-
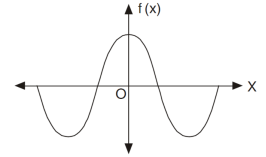
Area under the curve from -π to π will always be double the area from 0 to π
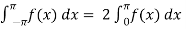
Expansion of an even function-
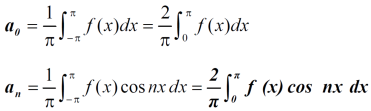
Here cos nx and f(x) are both even functions.
As we know that the product of two even numbers will be even.
Such as product of f(x) and cos nx will always be even.
Now,
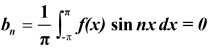
Here we see that sin nx is an odd function.
So that we do not need to find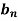 
That means the series of an even function contains cosine terms only.
Expansion of an odd function-
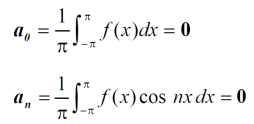
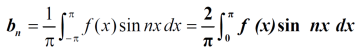
The series of the odd function contains only sine terms.
Example: Find the fourier expression of f(x) = x³ for –π < x < π.
Sol.
Here, we can see that f(x) Is an odd function
So that,
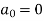and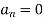 
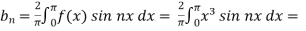
We will use here ,
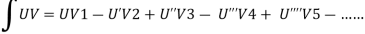
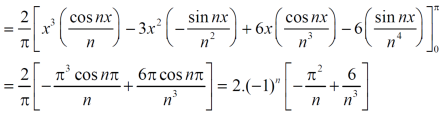
We get the value of f(x),
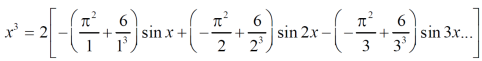
Example: Find the Fourier series expansion of the periodic function of period 2π.
f(x) = x² , -π≤x≤π
Sol. The given function is even, so that,
We will find 
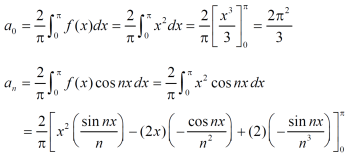
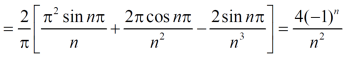
The fourier series will be ,
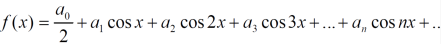
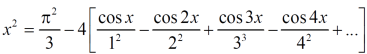
The function is defined in the interval(0,π) and it is immaterial whatever the function may be outside the interval (0,π)
To get the series of cosines only we suppose that f(x) is an even function in the interval (-π,π)
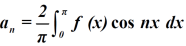
And bn = 0
To expand the as a sine series in the same interval and as an odd function.
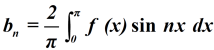
Bn = 0.
Example- Find a Fourier series for
; 
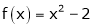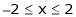
Solution:
Here
; 
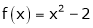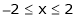
Since f(x) is even function hence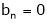 
It’s Fourier series is
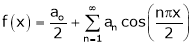… (1)
Where
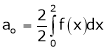
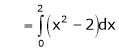
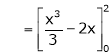
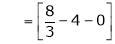
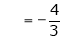
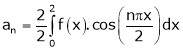
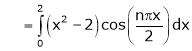
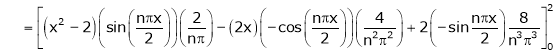
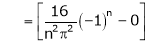
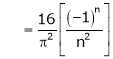
Hence equation (1) becomes,
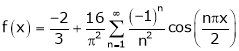
4. Find half range cosine series of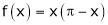 
in the interval 
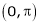and hence deduce that
a)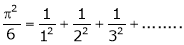 
b)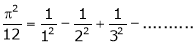 
Solution:
Here
; 
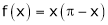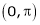
Hence it’s half range cosine series is,
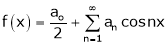… (1)
Where
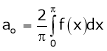
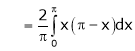
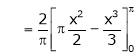
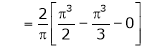
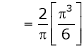
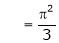
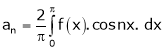
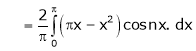
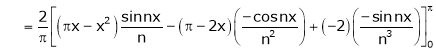
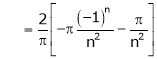
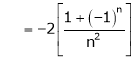
Hence equation (1) becomes,
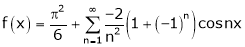
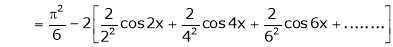
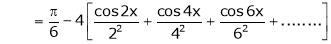… (2)
Put x = 0, we get
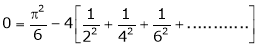
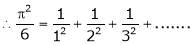
Hence the result
Put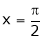 
we get,
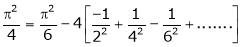
i.e. 
