UNIT 3 | unit 3 basic algorithms

PPS

UNIT- 3

Basic Algorithms

3.1 Basic Algorithms

Algorithm is a step-by-step procedure, which defines a set of instructions to be executed in a certain order to get the desired output. Algorithms are generally created independent of underlying languages, i.e. an algorithm can be implemented in more than one programming language.

From the data structure point of view, following are some important categories of algorithms −

Search− Algorithm to search an item in a data structure.
Sort− Algorithm to sort items in a certain order.
Insert− Algorithm to insert item in a data structure.
Update− Algorithm to update an existing item in a data structure.
Delete− Algorithm to delete an existing item from a data structure.

Characteristics of an Algorithm

Not all procedures can be called an algorithm. An algorithm should have the following characteristics −

Unambiguous− Algorithm should be clear and unambiguous. Each of its steps (or phases), and their inputs/outputs should be clear and must lead to only one meaning.
Input−An algorithm should have 0 or more well-defined inputs.
Output−An algorithm should have 1 or more well-defined outputs, and should match the desired output.
Finiteness− Algorithms must terminate after a finite number of steps.
Feasibility−Should be feasible with the available resources.
Independent−An algorithm should have step-by-step directions, which should be independent of any programming code.

How to Write an Algorithm?

There are no well-defined standards for writing algorithms. Rather, it is problem and resource dependent. Algorithms are never written to support a particular programming code.

As we know that all programming languages share basic code constructs like loops (do, for, while), flow-control (if-else), etc. These common constructs can be used to write an algorithm.

We write algorithms in a step-by-step manner, but it is not always the case. Algorithm writing is a process and is executed after the problem domain is well-defined. That is, we should know the problem domain, for which we are designing a solution.

Example

Let’s try to learn algorithm-writing by using an example.

Problem− Design an algorithm to add two numbers and display the result.

Step 1− START

Step 2− declare three integers a, b&c

Step 3− define values of a&b

Step 4− add values of a&b

Step 5− store output of step 4 to c

Step 6− print c

Step 7− STOP

Algorithms tell the programmers how to code the program. Alternatively, the algorithm can be written as −

Step 1− START ADD

Step 2− get values of a&b

Step 3− c ← a + b

Step 4− display c

Step 5− STOP

In design and analysis of algorithms, usually the second method is used to describe an algorithm. It makes it easy for the analyst to analyze the algorithm ignoring all unwanted definitions. He can observe what operations are being used and how the process is flowing.

Writing step numbers, is optional.

We design an algorithm to get a solution of a given problem. A problem can be solved in more than one ways.

Hence, many solution algorithms can be derived for a given problem. The next step is to analyze those proposed solution algorithms and implement the best suitable solution.

Algorithm Analysis

Efficiency of an algorithm can be analyzed at two different stages, before implementation and after implementation. They are the following −

A Priori Analysis−This is a theoretical analysis of an algorithm. Efficiency of an algorithm is measured by assuming that all other factors, for example, processor speed, are constant and have no effect on the implementation.
A Posterior Analysis−This is an empirical analysis of an algorithm. The selected algorithm is implemented using programming language. This is then executed on target computer machine. In this analysis, actual statistics like running time and space required, are collected.

We shall learn about a priori algorithm analysis. Algorithm analysis deals with the execution or running time of various operations involved. The running time of an operation can be defined as the number of computer instructions executed per operation.

Algorithm Complexity

Suppose X is an algorithm and n is the size of input data, the time and space used by the algorithm X are the two main factors, which decide the efficiency of X.

Time Factor− Time is measured by counting the number of key operations such as comparisons in the sorting algorithm.
Space Factor− Space is measured by counting the maximum memory space required by the algorithm.

The complexity of an algorithm f(n) gives the running time and/or the storage space required by the algorithm in terms of n as the size of input data.

Space Complexity

Space complexity of an algorithm represents the amount of memory space required by the algorithm in its life cycle. The space required by an algorithm is equal to the sum of the following two components −

A fixed part that is a space required to store certain data and variables, that are independent of the size of the problem. For example, simple variables and constants used, program size, etc.
A variable part is a space required by variables, whose size depends on the size of the problem. For example, dynamic memory allocation, recursion stack space, etc.

Space complexity S(P) of any algorithm P is S(P) = C + SP(I), where C is the fixed part and S(I) is the variable part of the algorithm, which depends on instance characteristic I. Following is a simple example that tries to explain the concept −

Algorithm: SUM(A, B)

Step 1 – START

Step 2 – C ← A + B + 10

Step 3 – Stop

Here we have three variables A, B, and C and one constant. Hence S(P) = 1 + 3. Now, space depends on data types of given variables and constant types and it will be multiplied accordingly.

Time Complexity

Time complexity of an algorithm represents the amount of time required by the algorithm to run to completion. Time requirements can be defined as a numerical function T(n), where T(n) can be measured as the number of steps, provided each step consumes constant time.

For example, addition of two n-bit integers takes n steps. Consequently, the total computational time is T(n) = c ∗ n, where c is the time taken for the addition of two bits. Here, we observe that T(n) grows linearly as the input size increases.

3.2 Searching

What is searching?

Searching is the process of finding a given value position in a list of values.
It decides whether a search key is present in the data or not.
It is the algorithmic process of finding a particular item in a collection of items.
It can be done on internal data structure or on external data structure.

Searching Techniques

To search an element in a given array, it can be done in following ways:

1. Sequential Search
2. Binary Search

1. Sequential Search

Sequential search is also called as Linear Search.
Sequential search starts at the beginning of the list and checks every element of the list.
It is a basic and simple search algorithm.
Sequential search compares the element with all the other elements given in the list. If the element is matched, it returns the value index, else it returns -1.

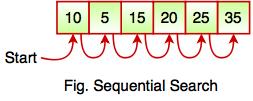
The above figure shows how sequential search works. It searches an element or value from an array till the desired element or value is not found. If we search the element 25, it will go step by step in a sequence order. It searches in a sequence order. Sequential search is applied on the unsorted or unordered list when there are fewer elements in a list.

The following code snippet shows the sequential search operation:

FunctionsearchValue(value, target)
{
      for (vari = 0; i<value.length; i++)
      {
             if (value[i] == target)
             {
                     return i;
             }
      }
      return -1;
}
searchValue([10, 5, 15, 20, 25, 35] , 25);   // Call the function with array and number to be searched

Example: Program for Sequential Search

#include <stdio.h>
int main()
{
   intarr[50], search, cnt, num;

   printf("Enter the number of elements in array\n");
   scanf("%d",&num);

   printf("Enter %d integer(s)\n", num);

   for (cnt = 0; cnt<num; cnt++)
   scanf("%d", &arr[cnt]);

   printf("Enter the number to search\n");
   scanf("%d", &search);

   for (cnt = 0; cnt<num; cnt++)
   {
      if (arr[cnt] == search)     /* if required element found */
      {
         printf("%d is present at location %d.\n", search, cnt+1);
         break;
      }
   }
   if (cnt == num)
      printf("%d is not present in array.\n", search);

   return 0;
}

Output:

sequential search output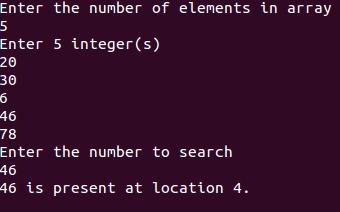

2. Binary Search

Binary Search is used for searching an element in a sorted array.
It is a fast search algorithm with run-time complexity of O(log n).
Binary search works on the principle of divide and conquer.
This searching technique looks for a particular element by comparing the middle most element of the collection.
It is useful when there are large number of elements in an array.

binary array

The above array is sorted in ascending order. As we know binary search is applied on sorted lists only for fast searching.

For example, if searching an element 25 in the 7-element array, following figure shows how binary search works: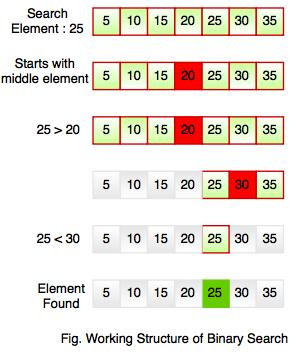

working structure binary search

Binary searching starts with middle element. If the element is equal to the element that we are searching then return true. If the element is less than then move to the right of the list or if the element is greater than then move to the left of the list. Repeat this, till you find an element.

Example: Program for Binary Search

#include<stdio.h>
#include<conio.h>

void main()
{
   int f, l, m, size, i, sElement, list[50]; //int f, l ,m : First, Last, Middle
   clrscr();

   printf("Enter the size of the list: ");
   scanf("%d",&size);

   printf("Enter %d integer values : \n", size);

   for (i = 0; i< size; i++)
      scanf("%d",&list[i]);

   printf("Enter value to be search: ");
   scanf("%d", &sElement);

   f = 0;
   l = size - 1;
   m = (f+l)/2;

   while (f <= l) {
      if (list[m] <sElement)
         f = m + 1;
      else if (list[m] == sElement) {
         printf("Element found at index %d.\n",m);
         break;
      }
      else
         l = m - 1;
      m = (f + l)/2;
   }
   if (f > l)
      printf("Element Not found in the list.");
   getch();
}

Output: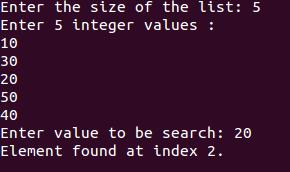

binary search output

3.3 Basic Sorting Algorithms (Bubble, Insertion and Selection)

Bubble Sort

In Bubble sort, Each element of the array is compared with its adjacent element. The algorithm processes the list in passes. A list with n elements requires n-1 passes for sorting. Consider an array A of n elements whose elements are to be sorted by using Bubble sort. The algorithm processes like following.

In Pass 1, A[0] is compared with A[1], A[1] is compared with A[2], A[2] is compared with A[3] and so on. At the end of pass 1, the largest element of the list is placed at the highest index of the list.
In Pass 2, A[0] is compared with A[1], A[1] is compared with A[2] and so on. At the end of Pass 2 the second largest element of the list is placed at the second highest index of the list.
In pass n-1, A[0] is compared with A[1], A[1] is compared with A[2] and so on. At the end of this pass. The smallest element of the list is placed at the first index of the list.

Algorithm :

Step 1: Repeat Step 2 For i = 0 to N-1
Step 2: Repeat For J = i + 1 to N - I
Step 3: IF A[J] > A[i]
SWAP A[J] and A[i]
[END OF INNER LOOP]
[END OF OUTER LOOP
Step 4: EXIT

Complexity

Scenario	Complexity
Space	O(1)
Worst case running time	O(n2)
Average case running time	O(n)
Best case running time	O(n2)

C Program

#include<stdio.h>
Void main ()
{
Int i, j,temp;
Int a[10] = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
For(i = 0; i<10; i++)
{
For(j = i+1; j<10; j++)
{
If(a[j] > a[i])
{
Temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
}
Printf("Printing Sorted Element List ...\n");
For(i = 0; i<10; i++)
{
Printf("%d\n",a[i]);
}
}

Output:

Printing Sorted Element List . . .

101

C++ Program

#include<iostream>
Using namespace std;
Int main ()
{
Int i, j,temp;
Int a[10] = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
For(i = 0; i<10; i++)
{
For(j = i+1; j<10; j++)
{
If(a[j] < a[i])
{
Temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
}
Cout <<"Printing Sorted Element List ...\n";
For(i = 0; i<10; i++)
{
Cout <<a[i]<<"\n";
}
Return 0;
}

Output:

Printing Sorted Element List ...

101

Java Program

Public class BubbleSort {
Public static void main(String[] args) {
Int[] a = {10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
For(int i=0;i<10;i++)
{
For (int j=0;j<10;j++)
{
If(a[i]<a[j])
{
Int temp = a[i];
a[i]=a[j];
a[j] = temp;
}
}
}
System.out.println("Printing Sorted List ...");
For(int i=0;i<10;i++)
{
System.out.println(a[i]);
}
}
}

Output:

Printing Sorted List . . .

101

C# Program

Using System;
Public class Program
{
Public static void Main()
{
Int i, j,temp;
Int[] a = {10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
For(i = 0; i<10; i++)
{
For(j = i+1; j<10; j++)
{
If(a[j] > a[i])
{
Temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
}
Console.WriteLine("Printing Sorted Element List ...\n");
For(i = 0; i<10; i++)
{
Console.WriteLine(a[i]);
}
}
}

Output:

Printing Sorted Element List . . .

101

Python Program

a=[10, 9, 7, 101, 23, 44, 12, 78, 34, 23]
For i in range(0,len(a)):
For j in range(i+1,len(a)):
If a[j]<a[i]:
Temp = a[j]
a[j]=a[i]
a[i]=temp
Print("Printing Sorted Element List...")
For i in a:
Print(i)

Output:

Printing Sorted Element List . . .

101

Rust Program

Fn main()
{
Let mut temp;
Let mut a: [i32; 10] = [10, 9, 7, 101, 23, 44, 12, 78, 34, 23];
For i in 0..10
{
For j in (i+1)..10
{
If a[j] < a[i]
{
Temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
}
Println!("Printing Sorted Element List ...\n");
For i in &a
{
Println!("{} ",i);
}
}

Output:

Printing Sorted Element List . . .

101

JavaScript Program

<html>
<head>
<title>
Bubble Sort
</title>
</head>
<body>
<script>
Var a = [10, 9, 7, 101, 23, 44, 12, 78, 34, 23];
For(i=0;i<10;i++)
{
For (j=0;j<10;j++)
{
If(a[i]<a[j])
{
Temp = a[i];
a[i]=a[j];
a[j] = temp;
}
}
}
Txt = "<br>";
Document.writeln("Printing Sorted Element List ..."+txt);
For(i=0;i<10;i++)
{
Document.writeln(a[i]);
Document.writeln(txt);
}
</script>
</body>
</html>

Output:

Printing Sorted Element List ...

101

PHP Program

<html>
<head>
<title>Bubble Sort</title>
</head>
<body>
<?php
$a = array(10, 9, 7, 101, 23, 44, 12, 78, 34, 23);
For($i=0;$i<10;$i++)
{
For ($j=0;$j<10;$j++)
{
If($a[$i]<$a[$j])
{
$temp = $a[$i];
$a[$i]=$a[$j];
$a[$j] = $temp;
}
}
}
Echo "Printing Sorted Element List ...\n";
For($i=0;$i<10;$i++)
{
Echo $a[$i];
Echo "\n";
}
?>
</body>
</html>

Output:

Printing Sorted Element List ...

101

Insertion Sort

Insertion sort is the simple sorting algorithm which is commonly used in the daily lives while ordering a deck of cards. In this algorithm, we insert each element onto its proper place in the sorted array. This is less efficient than the other sort algorithms like quick sort, merge sort, etc.

Technique

Consider an array A whose elements are to be sorted. Initially, A[0] is the only element on the sorted set. In pass 1, A[1] is placed at its proper index in the array.

In pass 2, A[2] is placed at its proper index in the array. Likewise, in pass n-1, A[n-1] is placed at its proper index into the array.

To insert an element A[k] to its proper index, we must compare it with all other elements i.e. A[k-1], A[k-2], and so on until we find an element A[j] such that, A[j]<=A[k].

All the elements from A[k-1] to A[j] need to be shifted and A[k] will be moved to A[j+1].

Complexity

Complexity	Best Case	Average Case	Worst Case
Time	Ω(n)	θ(n2)	o(n2)
Space			o(1)

Algorithm

Step 1: Repeat Steps 2 to 5 for K = 1 to N-1
Step 2: SET TEMP = ARR[K]
Step 3: SET J = K - 1
Step 4: Repeat while TEMP <=ARR[J]
SET ARR[J + 1] = ARR[J]
SET J = J - 1
[END OF INNER LOOP]
Step 5: SET ARR[J + 1] = TEMP
[END OF LOOP]
Step 6: EXIT

C Program

#include<stdio.h>
Void main ()
{
Int i,j, k,temp;
Int a[10] = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
Printf("\nprinting sorted elements...\n");
For(k=1; k<10; k++)
{
Temp = a[k];
j= k-1;
While(j>=0 && temp <= a[j])
{
a[j+1] = a[j];
j = j-1;
}
a[j+1] = temp;
}
For(i=0;i<10;i++)
{
Printf("\n%d\n",a[i]);
}
}

Output:

Printing Sorted Elements . . .

101

C++ Program

#include<iostream>
Using namespace std;
Int main ()
{
Int i,j, k,temp;
Int a[10] = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
Cout<<"\nprinting sorted elements...\n";
For(k=1; k<10; k++)
{
Temp = a[k];
j= k-1;
While(j>=0 && temp <= a[j])
{
a[j+1] = a[j];
j = j-1;
}
a[j+1] = temp;
}
For(i=0;i<10;i++)
{
Cout <<a[i]<<"\n";
}
}

Output:

Printing sorted elements...

101

Java Program

Public class InsertionSort {
Public static void main(String[] args) {
Int[] a = {10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
For(int k=1; k<10; k++)
{
Int temp = a[k];
Int j= k-1;
While(j>=0 && temp <= a[j])
{
a[j+1] = a[j];
j = j-1;
}
a[j+1] = temp;
}
System.out.println("printing sorted elements ...");
For(int i=0;i<10;i++)
{
System.out.println(a[i]);
}
}
}

Output:

Printing sorted elements . . .

101

C# Program

Using System;
Public class Program
{
Public static void Main()
{
Int i,j, k,temp;
Int[] a = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
Console.WriteLine("\nprinting sorted elements...\n");
For(k=1; k<10; k++)
{
Temp = a[k];
j= k-1;
While(j>=0 && temp <= a[j])
{
a[j+1] = a[j];
j = j-1;
}
a[j+1] = temp;
}
For(i=0;i<10;i++)
{
Console.WriteLine(a[i]);
}
}
}

Output:

Printing sorted elements . . .

101

Python Program

a=[10, 9, 7, 101, 23, 44, 12, 78, 34, 23]
For k in range(1,10):
Temp = a[k]
j = k-1
While j>=0 and temp <=a[j]:
a[j+1]=a[j]
j = j-1
a[j+1] = temp
Print("printing sorted elements...")
For i in a:
Print(i)

Output:

Printing sorted elements . . .

101

Swift Program

Import Foundation
Import Glibc
Var a = [10, 9, 7, 101, 23, 44, 12, 78, 34, 23];
Print("\nprinting sorted elements...\n");
For k in 1...9
{
Let temp = a[k];
Var j = k-1;
While j>=0 && temp <= a[j]
{
a[j+1] = a[j];
j = j-1;
}
a[j+1] = temp;
}
For i in a
{
Print(i);
}

Output:

Printing sorted elements...

101

JavaScript Program

<html>
<head>
<title>
Insertion Sort
</title>
</head>
<body>
<script>
Var txt = "<br>";
Var a = [10, 9, 7, 101, 23, 44, 12, 78, 34, 23];
Document.writeln("printing sorted elements ... "+txt);
For(k=0;k<10;k++)
{
Var temp = a[k]
j=k-1;
While (j>=0 && temp <= a[j])
{
a[j+1] = a[j];
jj = j-1;
}
a[j+1] = temp;
}
For(i=0;i<10;i++)
{
Document.writeln(a[i]);
Document.writeln(txt);
}
</script>
</body>
</html>

Output:

Printing sorted elements ...

101

PHP Program

<html>
<head>
<title>Insertion Sort</title>
</head>
<body>
<?php
$a = array(10, 9, 7, 101, 23, 44, 12, 78, 34, 23);
Echo("printing sorted elements ... \n");
For($k=0;$k<10;$k++)
{
$temp = $a[$k];
$j=$k-1;
While ($j>=0 && $temp <= $a[$j])
{
$a[$j+1] = $a[$j];
$j = $j-1;
}
$a[$j+1] = $temp;
}
For($i=0;$i<10;$i++)
{
Echo $a[$i];
Echo "\n";
}
?>
</body>
</html>

Output:

Printing sorted elements ...

101

Selection Sort

In selection sort, the smallest value among the unsorted elements of the array is selected in every pass and inserted to its appropriate position into the array.

First, find the smallest element of the array and place it on the first position. Then, find the second smallest element of the array and place it on the second position. The process continues until we get the sorted array.

The array with n elements is sorted by using n-1 pass of selection sort algorithm.

In 1st pass, smallest element of the array is to be found along with its index pos. Then, swap A[0] and A[pos]. Thus A[0] is sorted, we now have n -1 elements which are to be sorted.
In 2nd pas, position pos of the smallest element present in the sub-array A[n-1] is found. Then, swap, A[1] and A[pos]. Thus A[0] and A[1] are sorted, we now left with n-2 unsorted elements.
In n-1th pass, position pos of the smaller element between A[n-1] and A[n-2] is to be found. Then, swap, A[pos] and A[n-1].

Therefore, by following the above explained process, the elements A[0], A[1], A[2],...., A[n-1] are sorted.

Example

Consider the following array with 6 elements. Sort the elements of the array by using selection sort.

A = {10, 2, 3, 90, 43, 56}.

Pass	Pos	A[0]	A[1]	A[2]	A[3]	A[4]	A[5]
1	1	2	10	3	90	43	56
2	2	2	3	10	90	43	56
3	2	2	3	10	90	43	56
4	4	2	3	10	43	90	56
5	5	2	3	10	43	56	90

Sorted A = {2, 3, 10, 43, 56, 90}

Complexity

Complexity	Best Case	Average Case	Worst Case
Time	Ω(n)	θ(n2)	o(n2)
Space			o(1)

Algorithm

SELECTION SORT(ARR, N)

Step 1: Repeat Steps 2 and 3 for K = 1 to N-1
Step 2: CALL SMALLEST(ARR, K, N, POS)
Step 3: SWAP A[K] with ARR[POS]
[END OF LOOP]
Step 4: EXIT

SMALLEST (ARR, K, N, POS)

Step 1: [INITIALIZE] SET SMALL = ARR[K]
Step 2: [INITIALIZE] SET POS = K
Step 3: Repeat for J = K+1 to N -1
IF SMALL > ARR[J]
SET SMALL = ARR[J]
SET POS = J
[END OF IF]
[END OF LOOP]
Step 4: RETURN POS

C Program

#include<stdio.h>
Int smallest(int[],int,int);
Void main ()
{
Int a[10] = {10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
Int i,j,k,pos,temp;
For(i=0;i<10;i++)
{
Pos = smallest(a,10,i);
Temp = a[i];
a[i]=a[pos];
a[pos] = temp;
}
Printf("\nprinting sorted elements...\n");
For(i=0;i<10;i++)
{
Printf("%d\n",a[i]);
}
}
Int smallest(int a[], int n, int i)
{
Int small,pos,j;
Small = a[i];
Pos = i;
For(j=i+1;j<10;j++)
{
If(a[j]<small)
{
Small = a[j];
Pos=j;
}
}
Return pos;
}

Output:

Printing sorted elements...

101

C++ Program

#include<iostream>
Using namespace std;
Int smallest(int[],int,int);
Int main ()
{
Int a[10] = {10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
Int i,j,k,pos,temp;
For(i=0;i<10;i++)
{
Pos = smallest(a,10,i);
Temp = a[i];
a[i]=a[pos];
a[pos] = temp;
}
Cout<<"\n printing sorted elements...\n";
For(i=0;i<10;i++)
{
Cout<<a[i]<<"\n";
}
Return 0;
}
Int smallest(int a[], int n, int i)
{
Int small,pos,j;
Small = a[i];
Pos = i;
For(j=i+1;j<10;j++)
{
If(a[j]<small)
{
Small = a[j];
Pos=j;
}
}
Return pos;
}

Output:

Printing sorted elements...

101

Java Program

Public class SelectionSort {
Public static void main(String[] args) {
Int[] a = {10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
Int i,j,k,pos,temp;
For(i=0;i<10;i++)
{
Pos = smallest(a,10,i);
Temp = a[i];
a[i]=a[pos];
a[pos] = temp;
}
System.out.println("\nprinting sorted elements...\n");
For(i=0;i<10;i++)
{
System.out.println(a[i]);
}
}
Public static int smallest(int a[], int n, int i)
{
Int small,pos,j;
Small = a[i];
Pos = i;
For(j=i+1;j<10;j++)
{
If(a[j]<small)
{
Small = a[j];
Pos=j;
}
}
Return pos;
}
}

Output:

Printing sorted elements...

101

C# Program

Using System;
Public class Program
{
Public void Main() {
Int[] a = {10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
Int i,pos,temp;
For(i=0;i<10;i++)
{
Pos = smallest(a,10,i);
Temp = a[i];
a[i]=a[pos];
a[pos] = temp;
}
Console.WriteLine("\nprinting sorted elements...\n");
For(i=0;i<10;i++)
{
Console.WriteLine(a[i]);
}
}
Public static int smallest(int[] a, int n, int i)
{
Int small,pos,j;
Small = a[i];
Pos = i;
For(j=i+1;j<10;j++)
{
If(a[j]<small)
{
Small = a[j];
Pos=j;
}
}
Return pos;
}
}

Output:

Printing sorted elements...

101

Python Program

Def smallest(a,i):
Small = a[i]
Pos=i
For j in range(i+1,10):
If a[j] < small:
Small = a[j]
Pos = j
Return pos
a=[10, 9, 7, 101, 23, 44, 12, 78, 34, 23]
For i in range(0,10):
Pos = smallest(a,i)
Temp = a[i]
a[i]=a[pos]
a[pos]=temp
Print("printing sorted elements...")
For i in a:
Print(i)

Output:

Printing sorted elements...

101

Rust Program

Fn main ()
{
Let mut a: [i32;10] = [10, 9, 7, 101, 23, 44, 12, 78, 34, 23];
For i in 0..10
{
Let mut small = a[i];
Let mut pos = i;
For j in (i+1)..10
{
If a[j]<small
{
Small = a[j];
Pos=j;
}
}
Let mut temp = a[i];
a[i]=a[pos];
a[pos] = temp;
}
Println!("\nprinting sorted elements...\n");
For i in &a
{
Println!("{}",i);
}
}

Output:

Printing sorted elements...

101

JavaScript Program

<html>
<head>
<title>
Selection Sort
</title>
</head>
<body>
<script>
Function smallest(a, n, i)
{
Var small = a[i];
Var pos = i;
For(j=i+1;j<10;j++)
{
If(a[j]<small)
{
Small = a[j];
Pos=j;
}
}
Return pos;
}
Var a = [10, 9, 7, 101, 23, 44, 12, 78, 34, 23];
For(i=0;i<10;i++)
{
Pos = smallest(a,10,i);
Temp = a[i];
a[i]=a[pos];
a[pos] = temp;
}
Document.writeln("printing sorted elements ...\n"+"<br>");
For(i=0;i<10;i++)
{
Document.writeln(a[i]+"<br>");
}
</script>
</body>
</html>

Output:

Printing sorted elements ...

101

PHP Program

<html>
<head>
<title>Selection sort</title>
</head>
<body>
<?php
Function smallest($a, $n, $i)
{
$small = $a[$i];
$pos = $i;
For($j=$i+1;$j<10;$j++)
{
If($a[$j]<$small)
{
$small = $a[$j];
$pos=$j;
}
}
Return $pos;
}
$a = array(10, 9, 7, 101, 23, 44, 12, 78, 34, 23);
For($i=0;$i<10;$i++)
{
$pos = smallest($a,10,$i);
$temp = $a[$i];
$a[$i]=$a[$pos];
$a[$pos] = $temp;
}
Echo "printing sorted elements ...\n";
For($i=0;$i<10;$i++)
{
Echo $a[$i];
Echo "\n";
}
?>
</body>
</html>

Output:

Printing sorted elements ...

101

3.4 Finding roots of equations

The standard form of a quadratic equation is:

Ax2 + bx + c = 0, where

a, b and c are real numbers and

a != 0

The term b2-4ac is known as the discriminant of a quadratic equation. It tells the nature of the roots.

If the discriminant is greater than 0, the roots are real and different.
If the discriminant is equal to 0, the roots are real and equal.
If the discriminant is less than 0, the roots are complex and different.

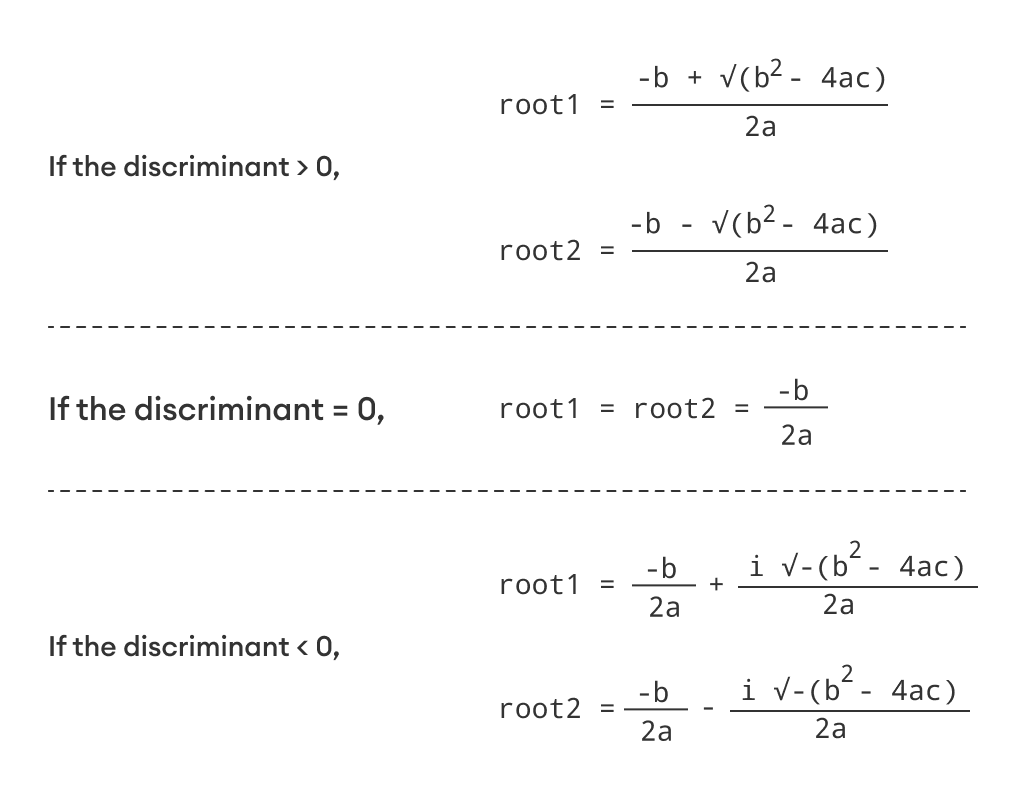
Formula to compute the roots of a quadratic equation

Figure: Roots of a Quadratic Equation

Program to Find Roots of a Quadratic Equation

#include <math.h>

#include <stdio.h>

Int main() {

Double a, b, c, discriminant, root1, root2, realPart, imagPart;

Printf("Enter coefficients a, b and c: ");

Scanf("%lf %lf %lf", &a, &b, &c);

Discriminant = b * b - 4 * a * c;

// condition for real and different roots

If (discriminant > 0) {

Root1 = (-b + sqrt(discriminant)) / (2 * a);

Root2 = (-b - sqrt(discriminant)) / (2 * a);

Printf("root1 = %.2lf and root2 = %.2lf", root1, root2);

}

// condition for real and equal roots

Else if (discriminant == 0) {

Root1 = root2 = -b / (2 * a);

Printf("root1 = root2 = %.2lf;", root1);

}

// if roots are not real

Else {

RealPart = -b / (2 * a);

ImagPart = sqrt(-discriminant) / (2 * a);

Printf("root1 = %.2lf+%.2lfi and root2 = %.2f-%.2fi", realPart, imagPart, realPart, imagPart);

}

Return 0;

}

Output

Enter coefficients a, b and c: 2.3

5.6

Root1 = -0.87+1.30i and root2 = -0.87-1.30i

In this program, the sqrt() library function is used to find the square root of a number.

3.5 Notion of order of complexity through example programs (no formal definition required)

Sometimes, there are more than one way to solve a problem. We need to learn how to compare the performance different algorithms and choose the best one to solve a particular problem. While analyzing an algorithm, we mostly consider time complexity and space complexity. Time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the length of the input. Similarly, Space complexity of an algorithm quantifies the amount of space or memory taken by an algorithm to run as a function of the length of the input.

Time and space complexity depends on lots of things like hardware, operating system, processors, etc. However, we don't consider any of these factors while analyzing the algorithm. We will only consider the execution time of an algorithm.

Lets start with a simple example. Suppose you are given an array

And an integer and you have to find if exists in array

Simple solution to this problem is traverse the whole array

And check if the any element is equal to

Fori : 1 to length of A

If A[i] is equal to x

Return TRUE

Return FALSE

Each of the operation in computer take approximately constant time. Let each operation takes

Time. The number of lines of code executed is actually depends on the value of . During analyses of algorithm, mostly we will consider worst case scenario, i.e., when is not present in the array . In the worst case, the if condition will run times where is the length of the array . So in the worst case, total execution time will be .for the if condition and for the return statement ( ignoring some operations like assignment of

As we can see that the total time depends on the length of the array

. If the length of the array will increase the time of execution will also increase.

Order of growth is how the time of execution depends on the length of the input. In the above example, we can clearly see that the time of execution is linearly depends on the length of the array. Order of growth will help us to compute the running time with ease. We will ignore the lower order terms, since the lower order terms are relatively insignificant for large input. We use different notation to describe limiting behavior of a function.

-notation:
To denote asymptotic upper bound, we use -notation. For a given function , we denote by (pronounced “big-oh of g of n”) the set of functions:
{ : there exist positive constants and such that for all

}

-notation:
To denote asymptotic lower bound, we use -notation. For a given function , we denote by (pronounced “big-omega of g of n”) the set of functions:
{ : there exist positive constants and such that for all

}

-notation:
To denote asymptotic tight bound, we use -notation. For a given function , we denote by (pronounced “big-theta of g of n”) the set of functions:
{ : there exist positive constants and such that for all

}

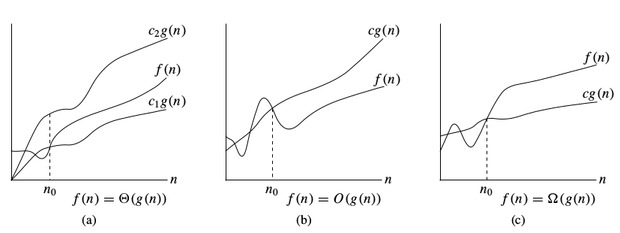
Time complexity notations

While analysing an algorithm, we mostly consider

-notation because it will give us an upper limit of the execution time i.e. the execution time in the worst case.

To compute

-notation we will ignore the lower order terms, since the lower order terms are relatively insignificant for large input.
Let

Lets consider some example:

Int count = 0;

For (inti = 0; i< N; i++)

For (int j = 0; j <i; j++)

Count++;

Lets see how many times count++ will run.

When

, it will run times.
When , it will run times.
When , it will run

Times and so on.

Total number of times count++ will run is

. So the time complexity will be

Int count = 0;

For (inti = N; i> 0; i /= 2)

For (int j = 0; j <i; j++)

Count++;

This is a tricky case. In the first look, it seems like the complexity is .for the loop and for loop. But its wrong. Lets see why.

Think about how many times count++ will run.

When

, it will run times.
When , it will run times.
When , it will run

Times and so on.

Total number of times count++ will run is

. So the time complexity will be

The table below is to help you understand the growth of several common time complexities, and thus help you judge if your algorithm is fast enough to get an Accepted ( assuming the algorithm is correct ).

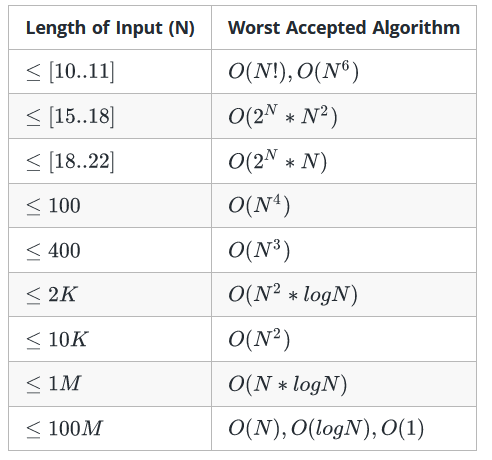
Text Books

(i) Byron Gottfried, Schaum's Outline of Programming with C, McGraw-Hill

(ii) E. Balaguruswamy, Programming in ANSI C, Tata McGraw-Hill

Reference Books

(i) Brian W. Kernighan and Dennis M. Ritchie, The C Programming Language, Prentice Hall of India.

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined