UNIT 3
WAVE-PARTICLE DUALITY
As we know in the Photoelectric Effect, the Compton Effect, and the pair production effect—radiation exhibits particle-like characteristics in addition to its wave nature. In 1923 de Broglie took things even further by suggesting that this wave–particle duality is not restricted to radiation, but must be universal.
In 1923, the French physicist Louis Victor de Broglie (1892-1987) put forward the bold hypothesis that moving particles of matter should display wave-like properties under suitable conditions.
All material particles should also display dual wave–particle behaviour. That is, the wave–particle duality present in light must also occur in matter.
So, starting from the momentum of a photon p = hν/c = h/λ.
We can generalize this relation to any material particle with nonzero rest mass. Each material particle of momentum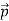 
behaves as a group of waves (matter waves) whose wavelength λ and wave vector 
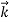are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed.
λ = 
=
…….(1) 
= 
…….(2)
Where ℏ = h/2π. The expression known as the de Broglie relation connects the momentum of a particle with the wavelength and wave vector of the wave corresponding to this particle. The wavelength λ of the matter wave is called de Broglie wavelength. The dual aspect of matter is evident in the de Broglie relation.
λ is the attribute of a wave while on the right-hand side the momentum p is a typical attribute of a particle. Planck’s constant h relates the two attributes. Equation (1) for a material particle is basically a hypothesis whose validity can be tested only by experiment.
However, it is interesting to see that it is satisfied also by a photon. For a photon, as we have seen, p = hν/c.
Therefore
= 
= λ
Example: What is the frequency of a photon with energy of 4.5 eV?
Solution:
E = (4.5 eV) x (1.60 x 10-19 J/eV) = 7.2 x 10-19 J
E = hf
h = 6.63 x 10-34 J x s
f = E / h = (7.2 x 10-19 J) / (6.63 x 10-34 J x s)
f = 1.1 x 1015 Hz
De Broglie’s Hypothesis: Matter Waves
Matter waves: According to De-Broglie, a wave is associated with each moving particle which is called matter waves.
As we know in the photoelectric effect, the Compton Effect, and the pair production effect radiation exhibits particle-like characteristics in addition to its wave nature. In 1923 de Broglie took things even further by suggesting that this wave–particle duality is not restricted to radiation, but must be universal:
All material particles should also display a dual wave–particle behaviour.
That is, the wave–particle duality present in light must also occur in matter. So, starting from the momentum of a photon p = h ν /c = h/λ, we can generalize this relation to any material particle with nonzero rest mass: each material particle of momentum 
behaves as a group of waves (matter waves) whose wavelength λ and wave vector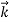
are governed by the speed and mass of the particle.
λ = 
= 
Wave has wavelength λ here h is Planck's constant and p is the momentum of the moving particle.
We have seen that microscopic particles, such as electrons, display wave behaviour. What about macroscopic objects? Do they also display wave features? They surely do. Although macroscopic material particles display wave properties, the corresponding wavelengths are too small to detect; being very massive, macroscopic objects have extremely small wavelengths.
At the microscopic level, however, the waves associated with material particles are of the same size or exceed the size of the system. Microscopic particles therefore exhibit clearly noticeable wave-like aspects.
The general rule is: whenever the de Broglie wavelength of an object is in the range of, or exceeds, its size, the wave nature of the object is detectable and hence cannot be neglected.
But if its de Broglie wavelength is much too small compared to its size, the wave behaviour of this object is undetectable.
For a quantitative illustration of this general rule, let us calculate in the following example the wavelengths corresponding to two particles, one microscopic (electron) and the other macroscopic (ball).
Example: What is the de Broglie wavelength associated with (a) an electron moving with a speed of 5.4×106 m/s, and (b) a ball of mass 150 g travelling at 30.0 m/s?
Solution:
(a)For the electron:
Mass m = 9.11×10–31 kg, speed v = 5.4×106 m/s.
Then, momentum
p = m v = 9.11×10–31 kg × 5.4 × 106 (m/s)
p = 4.92 × 10–24 kg m/s
De Broglie wavelength, λ = h/p = 6.63 x 10-34Js/ 4.92 × 10–24 kg m/s
λ= 0.135 nm
(b)For the ball:
Mass m’ = 0.150 kg,
Speed v ’= 30.0 m/s.
Then momentum p’ = m’ v’= 0.150 (kg) × 30.0 (m/s)
p’= 4.50 kg m/s
De Broglie wavelength λ’ = h/p’ =6.63 x 10-34Js/ 4.50 kg m/s =1.47 ×10–34 m
The de Broglie wavelength of electron is comparable with X-ray wavelengths. However, for the ball it is about 10–19 times the size of the proton, quite beyond experimental measurement.
With every physical observable there is associated a mathematical operator which is used in conjunction with the wavefunction. Suppose the wavefunction associated with a definite quantized value (eigenvalue) of the observable is denoted by Ψn (an eigenfunction) and the operator is denoted by Q. The action of the operator is given by
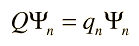
The mathematical operator Q extracts the observable value qn by operating upon the wavefunction which represents that particular state of the system. This process has implications about the nature of measurement in a quantum mechanical system. Any wavefunction for the system can be represented as a linear combination of the eigenfunctions Ψn, so the operator Q can be used to extract a linear combination of eigenvalues multiplied by coefficients related to the probability of their being observed.
With each measurable parameter in a physical system there is an associated quantum mechanical operator.
Need of operators arise because in quantum mechanics you are describing nature with waves (the wavefunction) rather than with discrete particles whose motion and dymamics can be described with the deterministic equations of Newtonian physics.
The operators associated with the parameters needed to describe the system. Some of those operators are listed below.
It is part of the basic structure of quantum mechanics that functions of position are unchanged in the Schrodinger equation, while momenta take the form of spatial derivatives. The Hamiltonian operator contains both time and space derivatives.
The quantum mechanical operator Q associated with a measurable property q must be Hermitian. Mathematically this property is defined by
Where Ψa and Ψb are arbitrary normalizable functions and the integration is over all of space. Physically, the Hermitian property is necessary in order for the measured values (eigenvalues) to be constrained to real numbers.
We are looking for expectation values of position and momentum knowing the state of the particle, i.e., the wave function ψ(x,t).
Position expectation:
= 
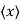What exactly does this mean?
It does not mean that if one measures the position of one particle over and over again, the average of the results will be given by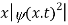 
On the contrary, the first measurement (whose outcome is indeterminate) will On the contrary, the first measurement (whose outcome is indeterminate) will collapse the wave function to a spike at the value actually obtained, and the subsequent measurements (if they're performed quickly) will simply repeat that same result.
Rather, <x> is the average of measurements performed on particles all in the state ψ, which means that either you must find some way of returning the particle to its original state after each measurement, or else you prepare a whole ensemble of particles, each in the same state ψ, and measure the positions of all of them: <x> is the average of these results. The position expectation may also be written as:
=
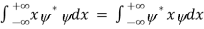To relate a quantum mechanical calculation to something you can observe in the laboratory, the "expectation value" of the measurable parameter is calculated. For the position x, the expectation value is defined as
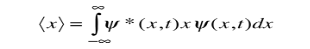
This integral can be interpreted as the average value of x that we would expect to obtain from a large number of measurements.
While the expectation value of a function of position has the appearance of an average of the function, the expectation value of momentum involves the representation of momentum as a quantum mechanical operator.
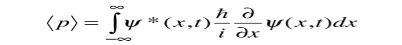
Where
Is the operator for the x component of momentum.
Since the energy of a free particle is given by
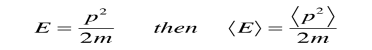
And the expectation value for energy becomes
For a particle in one dimension.
In general, the expectation value for any observable quantity is found by putting the quantum mechanical operator for that observable in the integral of the wavefunction over space:
Schrodinger wave equation, is the fundamental equation of quantum mechanics, same as the second law of motion is the fundamental equation of classical mechanics. This equation has been derived by Schrodinger in 1925 using the concept of wave function on the basis of de-Broglie wave and plank’s quantum theory.
Let us consider a particle of mass m and classically the energy of a particle is the sum of the kinetic and potential energies. We will assume that the potential is a function of only x.
So We have
E= K+V =
mv2+V(x) =
+V(x) ……….. (1)
By de Broglie’s relation we know that all particles can be represented as waves with frequency ω and wave number k, and that E= ℏω and p= ℏk.
Using this equation (1) for the energy will become
ℏω =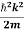 
+ V(x) ……….. (2)
A wave with frequency ω and wave number k can be written as usual as
ψ(x, t) =Aei(kx−ωt) ……….. (3)
The above equation is for one dimensional and for three dimensional we can write it as
ψ(r, t) =Aei(k·r−ωt) ……….. (4)
But here we will stick to one dimension only.
=−iωψ ⇒ ωψ=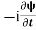
……….. (5)
=−k2ψ ⇒ k2ψ = -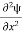 
……….. (6)
If we multiply the energy equation in Eq. (2) by ψ, and using(5) and (6) , we obtain
ℏ(ωψ) = 
ψ+ V(x) ψ ⇒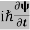 
= - 
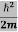
+ V(x) ψ ……….. (7)
This is the time-dependent Schrodinger equation.
If we put the x and t in above equation then equation (7) takes the form as given below
= - 
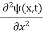+ V(x) ψ(x,t) ……….. (8)
In 3-D, the x dependence turns into dependence on all three coordinates (x, y, z) and the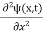 
term becomes ∇2ψ.
The term |ψ(x)|2 gives the probability of finding the particle at position x.
Let us again take it as simply a mathematical equation, then it’s just another wave equation. However We already know the solution as we used this function ψ(x, t) =Aei(kx−ωt) to produce Equations (5), (6) and (7)
But let’s pretend that we don’t know this, and let’s solve the Schrodinger equation as if we were given to us. As always, we will guess an exponential solution by looking at exponential behaviour in the time coordinate, our guess is ψ(x, t) =e−iωtf(x) putting this into Equation (7) and cancelling the e−iωt yields
= - 
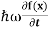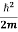
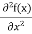+ V(x) f(x) ……….. (9)
We already know that E=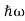
. However ψ(x, t) is general convention to also use the letter ψ to denote the spatial part. So, we will now replace f(x) with ψ(x)
Eψ = - 
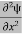+ V(x) ψ ……….. (10)
This is called the time-independent Schrodinger equation.
The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x.
The wave function ψ associated with a moving particle is not an observable quantity and does not have any direct physical meaning. It is a complex quantity. The complex wave function can be represented as
ψ(x, y, z, t) = a + ib
And its complex conjugate as
ψ*(x, y, z, t) = a – ib.
The product of wave function and its complex conjugate is
ψ(x, y, z, t)ψ*(x, y, z, t) = (a + ib) (a – ib) = a2 + b2
a2 + b2 is a real quantity.
However, this can represent the probability density of locating the particle at a place in a given instant of time.
The positive square root of ψ(x, y, z, t) ψ*(x, y, z, t) is represented as |ψ(x, y, z, t)|, called the modulus of ψ. The quantity |ψ(x, y, z, t)|2 is called the probability. This interpretation is possible because the product of a complex number with its complex conjugate is a real, non-negative number.
We should be able to find the particle somewhere, we should only find it at one place at a particular instant, and the total probability of finding it anywhere should be one.
For the probability interpretation to make sense, the wave function must satisfy certain conditions.
- The wave function must be single valued at each point.
- The probability of finding the particle at time t in an interval ∆x must be some number between 0 and 1.
- ψ must be finite everywhere.
- ψ must be continuous everywhere and
must also be continuous everywhere except where V(x) is infinite. - ψ (x) must vanish ψ
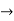0 as x
. - The wave function should satisfy the normalization condition. Normalization condition of a wave function ψ is mathematical statement of existence of the particle somewhere. So that if we sum up all possible values ∑|ψ(xi,t)|2∆xi we must obtain 1. The total probability of finding the particle anywhere must be one. Normalization condition is given as
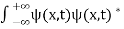dx =1
Only wave function with all these properties can yield physically meaningful result.
Physical significance of wave function
- The wave function ‘Ѱ’ has no physical meaning. It is a complex quantity representing the variation of a matter wave.
- The wave function Ѱ(r,t) describes the position of particle with respect to time .
- It can be considered as ‘probability amplitude’ since it is used to find the location of the particle.
- The square of the wave function gives the probability density of the particle which is represented by the wave function itself.
- More the value of probability density, more likely to find the particle in that region.
The Schrodinger equation also known as Schrodinger’s wave equation is a partial differential equation that describes the dynamics of quantum mechanical systems by the wave function. The trajectory, the positioning, and the energy of these systems can be retrieved by solving the Schrodinger equation.
All of the information for a subatomic particle is encoded within a wave function. The wave function will satisfy and can be solved by using the Schrodinger equation. The Schrodinger equation is one of the fundamental axioms that are introduced in undergraduate physics.
It is not possible to measure all properties of a quantum system precisely. Max Born suggested that the wave function was related to the probability that an observable has a specific value.
In any physical wave if ‘A’ is the amplitude of the wave, then the energy density i.e., energy per unit volume is equal to ‘A2’. Similar interpretation can be made in case of mater wave also. In matter wave, if ‘Ψ ‘is the wave function of matter waves at any point in space, then the particle density at that point may be taken as proportional to ‘Ψ2’. Thus, Ψ2 is a measure of particle density.
According to Max Born ΨΨ*=Ψ2 gives the probability of finding the particle in the state ‘Ψ’. i.e., ‘Ψ2’ is a measure of probability density. The probability of finding the particle in a volume (dv=dxdydz) is given by
= 
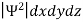
Since the particle has to be present somewhere, total probability of finding the particle somewhere is unity i.e., particle is certainly to be found somewhere in space. i.e.
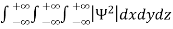=1
Or 
=1
This condition is called Normalization condition. A wave function which satisfies this condition is known as normalized wave function.
The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x.
Superposition is the ability of a quantum system to be in multiple states at the same time until it is measured. The superposition principle of quantum states, identified with the wave functions introduced by Schrödinger, is the fundamental property of quantum systems.
This principle provides the possibility to associate with two wave functions corresponding to the two pure states of the system, the third function which is an arbitrary linear combination of the two wave functions. A property of the quantum world is that this combination also corresponds to a physical state of the system. An analogous formulation takes place for two state vectors in a Hilbert space and the linear combination of these vectors.
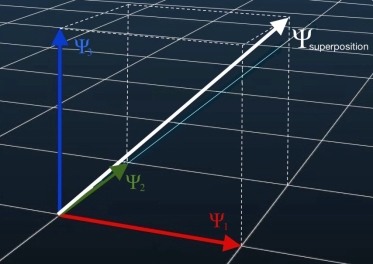
Figure:1
The foundation of quantum mechanics and the role of superposition principle were also discussed for quantum states, which are associated with the density matrices of density operators acting in the Hilbert space. The foundations of quantum optics were developed in connection with coherence properties of the electromagnetic-field states.
A phenomenon as interference of quantum states, described by the superposition principle of complex wave functions, is considered in the probability representation of quantum mechanics. In the probability picture, the interference is described by the nonlinear addition rule of the probabilities describing the superposed states; the rule provides the probabilities describing the superposition state, and this corresponds to the nonlinear addition rule of the projectors.
The superposition principle describes the interference phenomenon in quantum mechanics. Since the density operators
=|ψ1〉〈ψ1|
And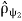 
=|ψ2〉〈ψ2|
Provide the expression for the density operator of superposition state |ψ〉〈ψ|, where vector |ψ〉is a linear combination of vectors|ψ1〉and|ψ2〉, the superposition principle can be formulated as an addition rule of the probabilities.
How do we account mathematically for the existence of the interference pattern in the double slit experiment with material particles such as electrons? An answer is offered by the superposition principle. The interference results from the superposition of the waves emitted by slits 1 and 2. If the functions
ψ1(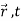
) and ψ2(
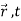), which denote the waves reaching the screen emitted respectively by slits 1 and 2, represent two physically possible states of the system, then any linear superposition
ψ(
) = 
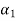ψ1(
) + 
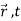ψ2(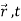
) …. (1)
Also represents a physically possible outcome of the system; ψ1 and ψ2 are complex constants.
This is the superposition principle. The intensity produced on the screen by opening only slit 1 is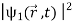 
and it is 
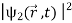when only slit 2 is open. When both slits are open, the intensity is
= 
= 
+ 
+ 
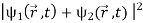
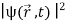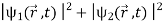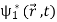
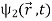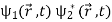… (2)
Where the asterisk denotes the complex conjugate. Note that (2) is not equal to the sum of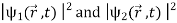 
it contains an additional term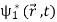 
+ 
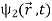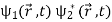
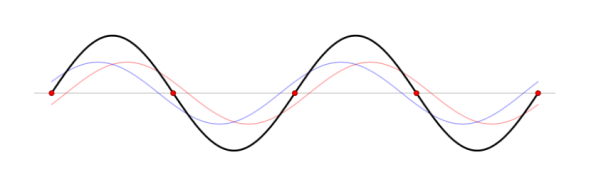
Figure: 2
This is the very term which gives rise in the case of electrons to an interference pattern similar to light waves. The interference pattern therefore results from the existence of a phase shift between 
and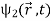 
. We can measure this phase shift from the interference pattern, but we can in no way measure the phases of 
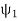and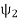 
separately.
We can summarize the double-slit results in three principles:
- Intensities add for classical particles: I = I1 + I2.
- Amplitudes, not intensities, add for quantum particles: ψ(
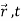) = ψ1(
) + ψ2(
) this gives rise to interference. - Whenever one attempts to determine experimentally the outcome of individual events for microscopic material particles (such as trying to specify the slit through which an electron has gone), the interference pattern gets destroyed. In this case the intensities add in much the same way as for classical particles: I = I1 + I2.
In computing, the concept of superposition has important implications for the way information will be processed and stored in the future. For example, today's classical computers process information in bits of one or zero, similar to a light switch being turned on or off. The quantum supercomputers of tomorrow, however, will process information as qubits -- one, zero or a superposition of the two states.
The state of a system does not have to be represented by a single wave function; it can be represented by a superposition of two or more wave functions. An example from the macroscopic world is a vibrating string; its state can be represented by a single wave or by the superposition (linear combination) of many waves. In this case the wavefunction can be represented by
|ψ〉= 
|ψi〉
Where the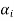 
are complex numbers. The quantity
P =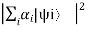 
Represents the probability for this superposition. If the states |ψi〉are mutually orthonormal, the probability will be equal to the sum of the individual probabilities:
P =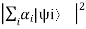 
= 
= P1 + P2+ P3 + P4 +…………..
Where Pi =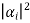
, Pi is the probability of finding the system in the state 
.
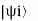A continuity equation is a differential equation that describes the conservative transport of some kind of quantity. Since mass, energy, momentum, and other natural quantities are conserved, a vast variety of physics may be described with continuity equations.
To set the stage we start with the Schrödinger Equation in Position Space.
= - 
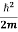∇2ψ(r,t) + V(r) ψ(r,t) ……….. (1)
And the complex conjugate of this equation
= - 
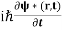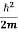∇2ψ*(r,t) + V(r) ψ*(r,t) ……….. (2)
The solution the Schrödinger Equation describes a particle with the normalised wave function ψ(r,t). Suppose a particle has a wave function ψ(r,t). We are interested in the probability of finding the particle.
We define the probability density as
ρ(r,t)=|ψ(r,t)|2
Since there is some chance of the particle moving into or out of r, this probability can change in time. At time t the probability dP(r,t) to find the particle at position r in the infinitesimal volume element dr3 is
DP(r,t)=|ψ(r,t)|2dr2=ρ(r,t)dr3
Now we multiply (1) by ψ∗(r,t) and (2) by ψ(r,t) and subtract (2) from (1). This gives
ψ∗(r,t)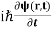
- ψ(r,t)
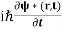= ψ∗(r,t) 
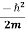∇2ψ(r,t) + V(r) ψ∗(r,t) ψ(r,t) - ψ(r,t) 
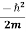∇2ψ*(r,t) - V(r) ψ(r,t)ψ*(r,t) ……….. (3)
On the LHS we can pull the derivative and iℏ in front to get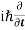 
ψ(r,t)ψ∗(r,t). On the RHS the potential terms simply cancel. So we have
|ψ(r,t)|2= ψ∗(r,t) 
∇2ψ(r,t) + - ψ(r,t) 
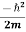∇2ψ*(r,t) ……….. (4)
Now we pull out the factor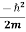 
and apply Greens first identity
∇⋅(ϕ∇ψ)=ϕ∇2ψ+∇ϕ∇ψ
On the RHS
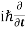|ψ(r,t)|2=
∇[ψ∗(r,t)∇ψ(r,t)−ψ(r,t)∇ψ∗(r,t)] ……….. (5)
Bringing iℏ on the other side we have
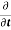|ψ(r,t)|2=
∇[ψ∗(r,t)∇ψ(r,t)−ψ(r,t)∇ψ∗(r,t)]
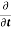|ψ(r,t)|2=∇
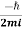[ψ(r,t)∇ψ∗(r,t)−ψ∗(r,t)∇ψ(r,t)] ………..(6)
We call the expression
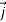(r,t)=
[ψ(r,t)∇ψ∗(r,t)−ψ∗(r,t)∇ψ(r,t)] ………..(7)
Is the probability current of the wave function ψ(r,t). Notice, j⃗ (r,t) is a real quantity since ψ(r,t)∇ψ∗(r,t) minus its complex conjugate gives an imaginary number, but we divide by i so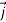 
(r,t) must be real.
Rewriting equation (7) using the probability density we find
The Continuity Equation for the probability density
= ∇. 
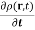(r,t) ……………(8)
With the probability current
(r,t) =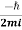 
[ψ(r,t)∇ψ∗(r,t)−ψ∗(r,t)∇ψ(r,t)]
This has the profound implication that the probability density is conserved
- ∇. 
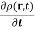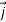(r,t) = 0 ……………(9)
Equation (9) should look familiar from E&M: it’s the same form as the equation for charge conservation. It says that the probability can change only by an amount equal to the flux of the “probability current ”J through the surface surrounding r. The current J therefore describes the flow of probability, the nearest thing we have in quantum mechanics to a description of the motion of a particle.
All the examples of continuity equations below express the same idea. Continuity equations are the (stronger) local form of conservation laws.
We shall now say that ρ is the probability of finding the electron in the volume element dV. ρ is called the probability density, and j is the probability current density.
We shall assume the potential V is independent of time. In this case the particle one dimensional Schrodinger equation can be solved using the method of separation of variables.
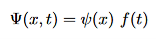
Recall that the one dimensional Schrodinger equation for a particle is
= - 
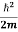
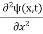+ V(x) ψ(x,t)
Which simplifies after separation to the following equation, where the left side depends only on time and the right side depends only on the position. The only way however for this to be true is if both sides are in fact constant, we call the constant E (this is in fact the energy of the particle as we show shortly after this).
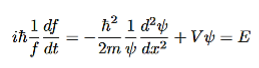
Which leads to
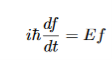
And
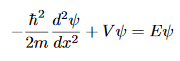
- The last equation is called The time-independent Schrodinger equation the solution of which correspond to a quantum state of definite energy (E).
In classical mechanics the total energy of a system (kinetic plus potential) is called hamiltonian H
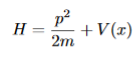
The corresponding Hamiltonian operator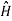 
can be obtained by substituting p with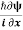 
Thus, the time-independent Schrodinger equation can be written as
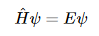
The expectation value of this operator is the total energy of the system (E) is
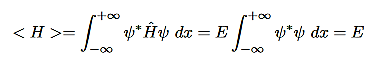
The standard deviation in H is given as
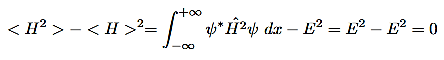
This means that repeated measurements on identical system described by the same state function will render the same energy
–Note that the system may have more than one allowable energy level
- The solution to original time dependent Schrodinger equation after separation becomes
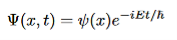
Although this solution depends on time, the probability density does not
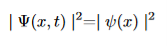
The same thing happens when calculating the expectation values of any dynamical variable Q(x,t)(Every expectation value is constant in time)
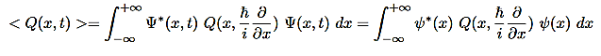
We say that the state function is stationary.
• The solution above is one of many other solutions to the time dependent Schrodinger equation, since the separation constant can take on any number of values. The acceptable values of E correspond to the allowable energy levels which can be discrete or continuous.
• Assuming discrete allowable energy levels ((E1,E2,E3,.....Emax), a much more general solution to the time dependent Schrodinger equation is of the form
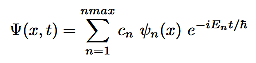
Where cn are constants to be determined from the initial state of the wave function Ψ(x,0)
• For a continuous energy spectrum
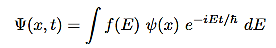
Where f(E) is a function of the energy E to be identified from the initial state of the wave function Ψ(x,0)
It so happens that every solution to the time dependent Schrodinger equation can be written in one of this form. It is simply a matter of finding the right constants (c1,c2,....)(for discrete energies) or f(E)for continuous energy spectrum so as to satisfy the initial condition of the problem.
The time independent Schrodinger Equation
………..(1)
For particles (such as electrons) bound in one dimensional potential wells. In general these solutions can be chosen to be real rather than complex functions which can often be considerable simplification. To see this let’s take the complex conjugate of the time independent SE given in Equation (1)
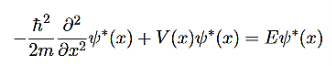………..(2)
Because all the factors which operate on ψ(x) are real, they don’t change under complex conjugation and hence ψ(x) and ψ∗(x) are equally valid solutions of the same potential V(x) with the same energy E.
Since the SE is a homogenous linear differential equation, we can always form new valid solutions by taking linear combinations of valid solutions. In particular, the solution ψr(x) which is constructed out of a general solutions ψ(x) and ψ∗(x) according to
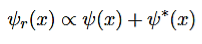………..(3)
Is an intrinsically real.
Of course exp(iϕ)×ψr(x) is an equally valid solution with any complex phase ϕ that one cares to choose.
Let us describe the general “potential well” illustrated below in hopefully familiar classical terms.
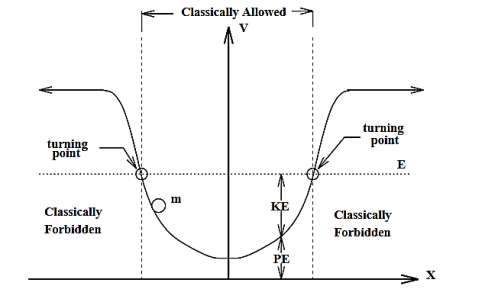
Figure:3
By a potential well, we mean a graph of potential energy as a function of coordinate x. In this well picture, we indicate a constant energy level (total potential plus kinetic energy) for the particle of mass m by the horizontal “dotted line”. The picture is meant to suggest conservation of energy i.e. the particle has the same total energy E= KE + PE independent of x. As a particle of mass m slides back and forth in x along the well much like a mass sliding down a frictionless valley, it constantly exchanges potential energy for kinetic energy while keeping a constant E.
The (energy) distance between the energy level and the potential curve rep-resents the kinetic energy since KE =E−V(x). Classically the kinetic energy is an intrinsically positive quantity because KE =mv2/2.
The classical turning points are the two intersections of the energy level and the potential well where the particle has zero kinetic energy.
In the region between the turning points E>V(x) and KE=E−V>0. Since the kinetic energy is positive this is a perfectly reasonable or “allowed” region for the particle to exist.
In the reason outside of the turning points, E<V(x) and KE=E−V<0 which is a classically “forbidden” condition. Classically the particle can never be found outside of the interval between the classical turning points.
Think of the particle as released from rest down at the left turning point on the frictionless gravitational valley represented by th potential, the particle picks up maximum speed at the bottom of the well, slows down as it approaches the right turning point. It stops at the right turning point, turns around and heads back down the well valley. Turning points where the particle turns around and reverses are aptly named.
If we have a particle in a box, where the ends of the box are absolute barriers that are infinitely high, then there is no probability of the particle existing outside the boundaries of the box. Since the particle’s wave function measures this probability, it has to be zero at the boundaries of the box, so that effectively pins down the particle at both ends. The fact that the wave function (in the case of the infinite square well) is a pure sine wave means that only those waves that go to zero at the ends of the box are permissible solutions, which in turn means that only multiples of half a full cycle of the sine wave are allowed as solutions, and since the energy of the particle is related to its wavelength, this requirement in turn puts restrictions on the allowable energies. That is, it is the act of confining the particle that results in the quantization of its energy, and the reason that confining the particle has this effect is that particle is defined by a wave function.
So ultimately it is the wave nature of the particle that causes the quantization. For potentials which go to infinity gradually (such as the harmonic oscillator) rather than abruptly (like the infinite square well), the particle is still being confined, but in a box with soft end points rather than hard ones. The wave is allowed to penetrate slightly into the barriers rather than be reflected from a hard surface, so its a bit like building a box with spongy walls rather than steel ones. There is a small chance that the particle can be found outside the end points of the box, but ultimately we are still confining the particle within a box. Going further with a qualitative description doesn’t help much, but we need to recognize that because the particle is still a wave, confining it within any type of box, no matter what type of endpoints the box has, will result in only certain wave functions being allowed. So ultimately it’s the boundary conditions that result in quantization of energy. The state of the particle is said to be bound by the potential or bound state.
What happens if the potential does not go to infinity at some point?
In that case, it is possible for the total energy of a particle to be greater than the maximum potential energy, which means that it is not restricted within a box. In that case, there is no restriction on energy levels of the particle, and in both the classical and quantum cases, the allowed energy levels are not quantized. In the quantum case, the particle still retains its wave-like qualities, but since the wave is not restricted by any barriers, there is no restriction on the allowable wavelengths, and thus, on the energies. The simplest example of such a case is that of the free particle, where a particle moves without any forces acting on it.
It should be added that potentials that don’t go to infinity at both ends can still give rise to bound states, if the total energy is less than the maximum value of the potential.
The point is that for a potential that is finite everywhere, any total energy that is greater than the maximum of the potential is possible, and these states are scattering states.
For a potential that goes to infinity at both ends, only bound, quantized states are possible. This is not to say that a particle whose total energy is greater than the maximum potential energy is unaffected by the presence of the potential.
If a particle, represented as a wave, travels in from the left(say) and encounters a potential barrier (or in fact, any change in the potential) at some point, then if the energy of the particle is greater than the barrier, there will be both reflected and transmitted components of the wave function past that point. Note that this doesn’t mean that the particle splits in two, with half of it being reflected and the other half transmitted. Rather, it is the wave function that effectively splits, and since the wave function is a measure of the probability of finding the particle at a given place and time, this means that there is now a certain probability that the particle (all of it!) will get reflected by the potential barrier, and another probability that it will get transmitted and proceed beyond the barrier.
These two types of quantum states are known as bound states (for states that are quantized, and in which the energy is constrained by a potential well that is infinite at both ends) and scattering states (for states where the potential fails to reach infinite height in either one or both directions).
