UNIT 4
FREE-PARTICLE SOLUTION
Our study of one-dimensional quantum mechanics begins with what you may think is a simple problem: that of a free particle. The Schrödinger equation for this system is as simple as it gets, after all, V(x) = 0.
A Free Particle
A particle is said to be free when no external force is acting on during its motion in the given region of space, and its potential energy V is constant.
Let us consider an electro is freely moving in space in positive x direction and not acted by any force, there potential will be zero. The Schrodinger wave equation reduces to
ψ +
E ψ =0
Substituting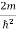 
E = k2
As the electron is moving in one direction (say x axis), then the above equation can be written as
+ k2 ψ =0
The general solution of the equation (2) is of the form ψ = ψ0e-iωt
The electron is not bounded and hence there are no restrictions on k. This implies that all the values of energy are allowed. The allowed energy values form a continuum and are given by
E =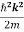 
The wave vector k describes the wave properties of the electron.
It is seen from the relation that E 
k2 Thus the plot of E as a function of k gives a parabola.
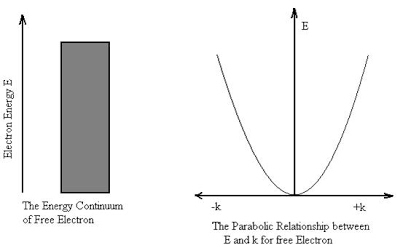
Figure 1
The momentum is well defined and, in this case given by
px ψ =
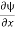
Therefore, according to uncertainty principle it is difficult to assign a position to the electron.
Let us consider a particle of mass ‘m’ in a deep well restricted to move in a one dimension (say x). Let us assume that the particle is free inside the well except during collision with walls from which it rebounds elastically.
The potential function is expressed as
V= 0 for 0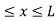
………. (1)
V=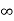 
for x <0, x>L ………. (2)
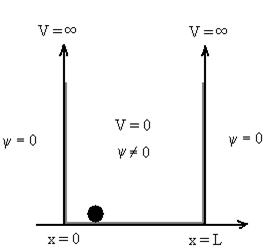
Figure 2: Particle in deep potential well
The probability of finding the particle outside the well is zero (i.e. Ѱ =0)
Inside the well, the Schrödinger wave equation is written as
ψ +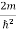
E ψ =0 …………….(2)
Substituting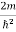 
E = k2 …………….(3)
Writing the SWE for 1-D we get
+ k2 ψ =0 …………….(4)
The general equation of above equation may be expressed as
ψ = Asin (kx + ϕ) …………….(5)
Where A and ϕ are constants to be determined by boundary conditions
Condition I: We have ψ = 0 at x = 0, therefore from equation
0 = A sinϕ
As A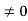 
then sinϕ =0 or ϕ=0 …………….(6)
Condition II: Further ψ = 0 at x = L, and ϕ=0 , therefore from equation (5)
0 = Asin kL
As A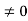 
then sinkL =0 or kL=nπ
k =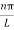 
…………….(7)
Where n= 1,2,3,4………
Substituting the value of k from (7) to (3)
)2 = 
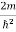E
This gives energy of level
En = 
n=1,2,3,4…so on …………….(8)
From equation En is the energy value (Eigen Value) of the particle in a well.
It is clear that the energy values of the particle in well are discrete not continuous.
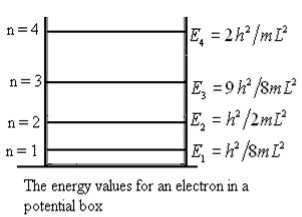
Figure:3
Using (6) and (7) equation (5) becomes, the corresponding wave functions will be
ψ = ψn = Asin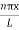
…………….(9)
The probability density
|ψ(x,t)|2 = ψ ψ*
|ψ(x,t)|2 = A2sin2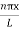
…………….(10)
The probability density is zero at x = 0 and x = L. Since the particle is always within the well
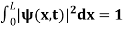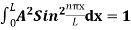
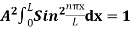
…………….(11)
=1
A =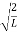 
Substituting A in equation (9) we get
ψ = ψn = 
sin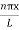
n=1,2,3,4….. …………….(12)
The above equation (12) is normalized wave function or Eigen function belonging to energy value En
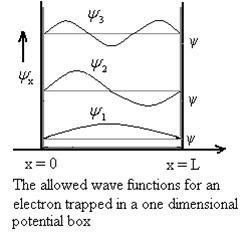
Figure 4: Wave function for Particle
We are looking for expectation values of position and momentum knowing the state of the particle, i.e., the wave function ψ(x,t).
Position expectation:
= 
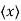What exactly does this mean?
It does not mean that if one measures the position of one particle over and over again, the average of the results will be given by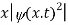 
On the contrary, the first measurement (whose outcome is indeterminate) will On the contrary, the first measurement (whose outcome is indeterminate) will collapse the wave function to a spike at the value actually obtained, and the subsequent measurements (if they're performed quickly) will simply repeat that same result.
Rather, <x> is the average of measurements performed on particles all in the state ψ, which means that either you must find some way of returning the particle to its original state after each measurement, or else you prepare a whole ensemble of particles, each in the same state ψ, and measure the positions of all of them: <x> is the average of these results. The position expectation may also be written as:
=
To relate a quantum mechanical calculation to something you can observe in the laboratory, the "expectation value" of the measurable parameter is calculated. For the position x, the expectation value is defined as
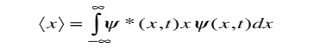
This integral can be interpreted as the average value of x that we would expect to obtain from a large number of measurements.
While the expectation value of a function of position has the appearance of an average of the function, the expectation value of momentum involves the representation of momentum as a quantum mechanical operator.
Where
Is the operator for the x component of momentum.
Since the energy of a free particle is given by
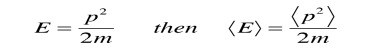
And the expectation value for energy becomes
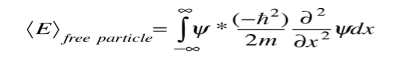
For a particle in one dimension.
In general, the expectation value for any observable quantity is found by putting the quantum mechanical operator for that observable in the integral of the wavefunction over space:
According to classical physics, given the initial conditions and the forces acting on a system, the future behaviour (unique path) of this physical system can be determined exactly. That is, if the initial coordinates
, velocity 
, and all the forces acting on the particle are known, the position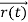 
, and velocity 
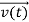are uniquely determined by means of Newton’s second law. So by Classical physics it can be easily derived.
Does this hold for the microphysical world?
Since a particle is represented within the context of quantum mechanics by means of a wave function corresponding to the particle’s wave, and since wave functions cannot be localized, then a microscopic particle is somewhat spread over space and, unlike classical particles, cannot be localized in space. In addition, we have seen in the double-slit experiment that it is impossible to determine the slit that the electron went through without disturbing it. The classical concepts of exact position, exact momentum, and unique path of a particle therefore make no sense at the microscopic scale. This is the essence of Heisenberg’s uncertainty principle.
In its original form, Heisenberg’s uncertainty principle states that: If the x-component of the momentum of a particle is measured with an uncertainty ∆px, then its x-position cannot, at the same time, be measured more accurately than ∆x = ℏ/(2∆px). The three-dimensional form of the uncertainty relations for position and momentum can be written as follows:
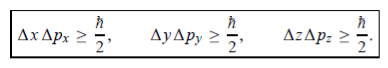
This principle indicates that, although it is possible to measure the momentum or position of a particle accurately, it is not possible to measure these two observables simultaneously to an arbitrary accuracy. That is, we cannot localize a microscopic particle without giving to it a rather large momentum.
We cannot measure the position without disturbing it; there is no way to carry out such a measurement passively as it is bound to change the momentum.
To understand this, consider measuring the position of a macroscopic object (you can consider a car) and the position of a microscopic system (you can consider an electron in an atom). On the one hand, to locate the position of a macroscopic object, you need simply to observe it; the light that strikes it and gets reflected to the detector (your eyes or a measuring device) can in no measurable way affect the motion of the object.
On the other hand, to measure the position of an electron in an atom, you must use radiation of very short wavelength (the size of the atom). The energy of this radiation is high enough to change tremendously the momentum of the electron; the mere observation of the electron affects its motion so much that it can knock it entirely out of its orbit.
It is therefore impossible to determine the position and the momentum simultaneously to arbitrary accuracy. If a particle were localized, its wave function would become zero everywhere else and its wave would then have a very short wavelength. According to de Broglie’s relation p = ℏ /λ,
Time Energy Uncertainty Relation
The momentum of this particle will be rather high. Formally, this means that if a particle is accurately localized (i.e., ∆x 
0), there will be total uncertainty about its momentum (i.e., ∆px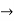 
∞).
Since all quantum phenomena are described by waves, we have no choice but to accept limits on our ability to measure simultaneously any two complementary variables.
Heisenberg’s uncertainty principle can be generalized to any pair of complementary, or canonically conjugate, dynamical variables: it is impossible to devise an experiment that can measure simultaneously two complementary variables to arbitrary accuracy. If this were ever achieved, the theory of quantum mechanics would collapse.
Energy and time, for instance, form a pair of complementary variables. Their simultaneous measurement must obey the time–energy uncertainty relation:
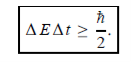
This relation states that if we make two measurements of the energy of a system and if these measurements are separated by a time interval ∆t, the measured energies will differ by an amount ∆E which can in no way be smaller than ℏ /∆t. If the time interval between the two measurements is large, the energy difference will be small. This can be attributed to the fact that, when the first measurement is carried out, the system becomes perturbed and it takes it a long time to return to its initial, unperturbed state. This expression is particularly useful in the study of decay processes, for it specifies the relationship between the mean lifetime and the energy width of the excited states.
In contrast to classical physics, quantum mechanics is a completely indeterministic theory. Asking about the position or momentum of an electron, one cannot get a definite answer; only a probabilistic answer is possible.
According to the uncertainty principle, if the position of a quantum system is well defined its momentum will be totally undefined.
1 Example: The uncertainty in the momentum of a ball travelling at 20m/s is 1×10−6 of its momentum. Calculate the uncertainty in position? Mass of the ball is given as 0.5kg.
Solution:
Given
v = 20m/s,
m = 0.5kg,
h = 6.626 × 10-34 m2 kg / s
Δp =p×1×10−6
As we know that,
P = m×v = 0.5×20 = 10kgm/s
Δp = 10×1×10−6
Δp = 10-5
Heisenberg Uncertainty principle formula is given as,
∆x∆p 
∆x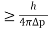 
∆x 
∆x =0.527 x 10-29 m
2 Example: The mass of a ball is 0.15 kg & its uncertainty in position to 10–10m. What is the value of uncertainty in its velocity?
Solution:
Given
m=0.15 kg.
h=6.6×10-34 Joule-Sec.
Δx = 10 –10 m
Δv=?
Δx.Δv ≥h/4πm
Δv≥h/4πmΔx
≥6.6×10-34/4×3.14×0.15×10–10
≥ 3.50×10–24m
Consider the following piecewise continuous, finite potential energy:
U=U0 x <0 (1)
U= 0 0
x
L (2)
U=U0 L < x. (3)
We want to solve Schroedinger’s Equation for this potential to get the wave functions and allowed energies for E < U0. We will refer to the three regions as regions 0, 1, and 2 with associated wave functions ψ0,ψ1,ψ2.
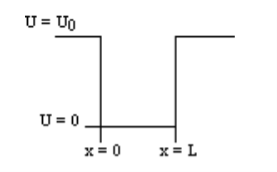
Figure 5: Finite Square Well Potential Energy
The time-invariant, non-relativistic Schroedinger’s equation is
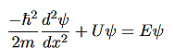(4)
That can be rearranged to give
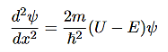(5)
It is convenient to define two new variables (both positive), one for regions 0 and 2, and one for region 1—they are wavenumbers:
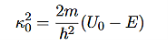(6)
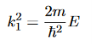(7)
And Schroedinger’s equation becomes
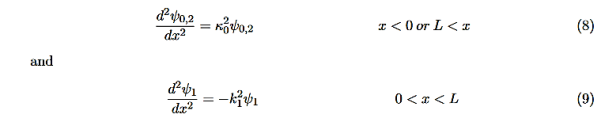
In regions 0 and 2 the general solution is a linear combination of exponentials with the same form, but with different constants, namely
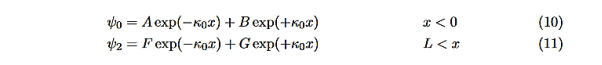
In region 1 we have the same general solution that we had for the infinite square well,
Equations (10) to (12) have 7 unknowns—A,B,C,D,F,G and the energy E that is im-plicitly contained in the variables κ0,k1. Therefore we need to get 7 equations to be ableto solve for the unknowns.
We will first use the requirement that the wavefunction remain finite everywhere. Consider ψ2 as x→∞. For this to remain finite we must require G= 0. Similarly, as x→−∞, we require A= 0. Our solutions become
The next step is to require that the wavefunction and its first derivative be continuous everywhere, and in our case, we look at the boundaries, x= 0 and x=L.
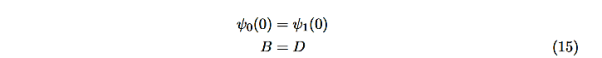
Hence ψ0=D exp(+κ0x). Take derivatives of the wave functions,
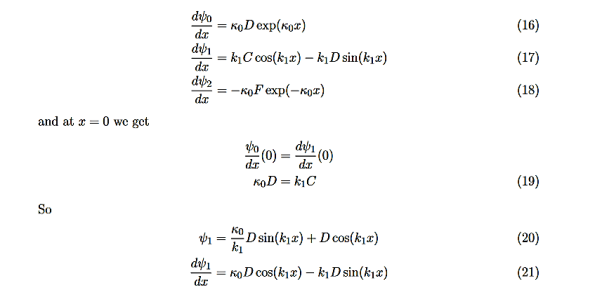
There remain 3 unknowns, D,F, and E. Finding them is a bit messier! Consider the boundary conditions at x=L,
We are not going much farther, but if we divided Equation (22) by Equation (23), we can see that the constants D and F cancel leaving us with one rather difficult equation to solve for energy E (remember this is implicitly included in the values of k1and κ0.)
There is one remaining condition, normalization, that for this problem is
Even without solving the entire problem we can make some conclusions about the wave-function and the allowed energy levels. Recall that for an infinite square well potential of width L the allowed energies are quantized and
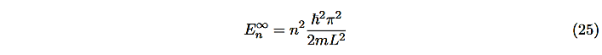
Here is Equation (22)/Equation (23)
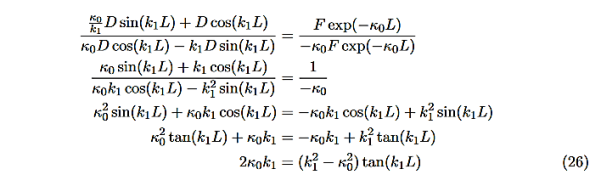
Now put in the values ofκ0andk1from Equations (6) and (7) and do some algebra to get
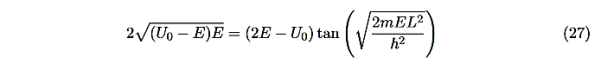
This equation is a single equation in a single unknown, E < U0. Once we have the details of our particle (its mass) and the potential energy (depth U0 and width L), we can solve it. There is no analytic solution, only a numerical one.
From equation (25) With n being any positive integer. Outside the well the wavefunction is 0. We are certain that the particle is somewhere inside the box, so ∆x ∞ =L.
With the finite well, the wavefunction is not zero outside the well,
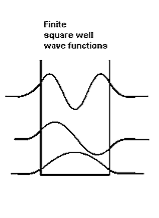
Figure 6
So ∆x finite> L, hence from the uncertainty principle, ∆pfinite x<∆p∞x. This suggests that the average value of momentum is less for the finite well, and therefore that the kinetic energy inside the well is less for the finite well than for the infinite well. Indeed, this is borne out with detailed analysis. In addition, the number of allowed energy levels is finite, and there is a possibility that a well may be sufficiently narrow or sufficiently shallow that no energy levels are allowed. Also note that the non-zero wavefunctions in regions 0 and 2 mean that there is a non-zero probability of finding the particle in a region that is classically forbidden, a region where the total energy is less than the potential energy so that the kinetic energy is negative.
The so-called tunnel effect of quantum mechanics can be derived from a special case of the potential well, by changing −V0 into +V0, thus creating a potential barrier, as seen in Figure 7.
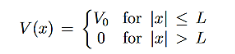
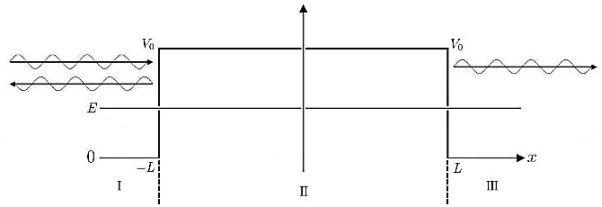
Figure 7: Tunnel effect: For a given potential barrier with height V0 the solutions of the Schrodinger equation with energy E < V0 still have a non-vanishing probability density in region III, which allows them to “tunnel” through the barrier although this would classically be forbidden.
Classically, a particle with less energy than the potential barrier could only be reflected. But in quantum mechanics, due to continuity the wave function decreases exponentially in the forbidden region II, resulting in a non-vanishing probability density in region III.
It allows the particle to pass the barrier as if it was through a tunnel, this linguistic illustration gives rise to the name tunnel effect.
Mathematically, we can use the solutions
…………(1)
Where
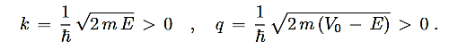…………(2)
Since the exponent of the solution in region II is not imaginary anymore, So we have solution in the form their hyperbolic counterparts
Tunneling – Transmission Coefficient
For the transmission amplitude we get the result
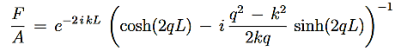…………(3)
Which, using the identity
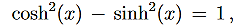…………(4)
Gives the transmission coefficient
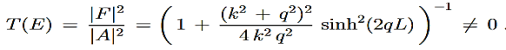…………(5)
It can be simplified under the condition that q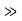
L1, which is a good approximationin most cases. Then
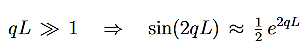…………(6)
And we can rewrite Equation (5) as
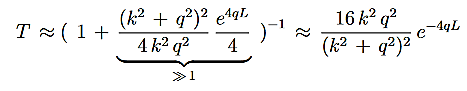…………(7)
We then use Equation (2) to express the transmission coefficient by the energy and potential strength to get
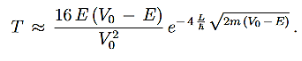…………(8)
Using exey=ex+y we can write the whole coefficient as an exponential function
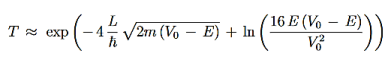…………(9)
Since we required that qL be much bigger than one and the logarithm increases only very slowly we can conclude that the first term in the exponent outweighs the second one, which we therefore neglect to obtain.
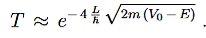…………(10)
We now have a good approximation for the transmission probability of a single potential step, constant in certain interval and vanishing outside. This potential is of course
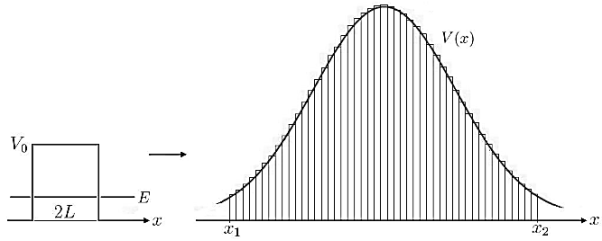
Figure 8: Calculation of Gamow factor: The generalization of the transmission coefficient, from a single constant potential barrier with width 2L, to the incorporation of a function V(x) is done straightforward by integration of infinitesimal potential barriers.
a very crude approximation of real-life potentials, which usually are more complicated functions of x. To meet these concerns we can generalize the transmission coefficient of Equation (10) to the so called Gamow factor by “chopping” a given potential in infinitesimal potential steps with constant values and integrating over a reasonable range [x1,x2]for which the potential stays above a certain value, see Figure 8.
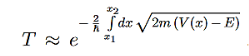
Physical Examples of Tunneling
We will now briefly present some examples, where the tunnel effect explains the observed phenomena.
Tunneling between conductors:
Imagine two conducting materials, separated by a thin insulating material, sketched in Figure 9. The tunnel effect then allows the electrons to tunnel through that barrier, thus creating a current. This effect is also observed for super conducting materials, where it is named Josephson effect.
Cold emission:
Electrons can be emitted from metals at very low temperatures, even without incident light if an exterior electric field is applied. Assuming that the electrons have a very low energy compared to the potential height, it is not very probable that an electron can tunnel through the potential barrier. Only if an electric field raises the energy of the electron, the transmission coefficient increases and the electron emission can be observed.
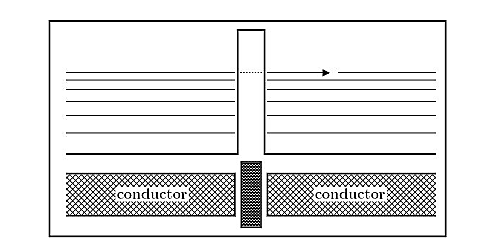
Figure 9: Tunneling through insulator: Between two conducting materials, separated by a thin insulating barrier, the tunnel effect creates a current.
Alpha decay:
In nuclear physics the tunnel effect plays an important role in the process of alpha decay. In the nucleus two protons and two neutrons can form a alpha-particle, i.e. a 4He nucleus, which due to the energy gain of the binding process, has the required energy to tunnel through the Coulomb-barrier, see Figure 10 E.g. The alpha decay of polonium to lead
212Po→208Pb+α
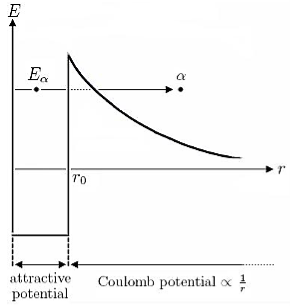
Figure 10: Alpha decay: The alpha particle formed in the nucleus has an energy boost due to the mass deficit of the binding process, which allows it to overcome the attractive strong force inside the nucleus and tunnel through the Coulomb barrier.
According to quantum free electron theory of metals, a conduction electron in a metal experiences constant (or zero) potential and free to move inside the crystal but will not come out of the metal because an infinite potential exists at the surface. This theory successfully explains electrical conductivity, specific heat, thermionic emission and para-magnetism. This theory is fails to explain many other physical properties, for example: (i) it fails to explain the difference between conductors, insulators and semiconductors, (ii) positive Hall coefficient of metals and (iii) lower conductivity of divalent metals than monovalent metals.
To overcome the above problems, the periodic potentials due to the positive ions in a metal have been considered as shown in Figure 4 (a), if an electron moves through these ions, it experiences varying potentials. The potential of an electron at the positive ion site is zero and is maximum in between two ions. The potential experienced by an electron, when it passes along a line through the positive ions is as shown in Figure 4 (b).
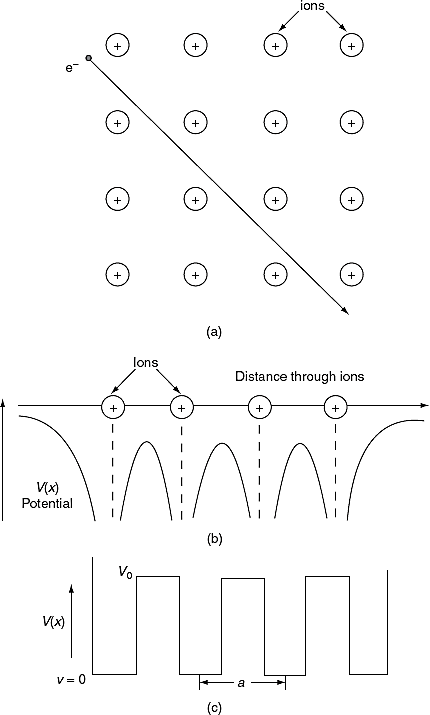
Figure 11
It is not easy to solve Schrödinger’s equation with these potentials. So, Kronig and Penney approximated these potentials inside the crystal to the shape of rectangular steps as shown in Figure 11(c). This model is called Kronig-Penney model of potentials.
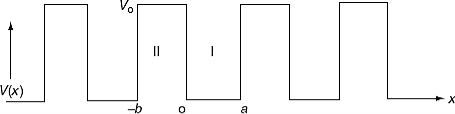
Figure 12
The energies of electrons can be known by solving Schrödinger’s wave equation in such a lattice.
The solution to Schrödinger's equation for the Kronig-Penney potential is obtained by assuming that the solution is a Bloch function, namely a traveling wave solution of the form, eikx, multiplied with a periodic solution, u(x), which has the same periodicity as the periodic potential. The total wave function is therefore of the form:
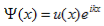
Where u(x) is the periodic function as defined by u(x) = u (x + a), and k(x) is the wave number. We now rewrite Schrödinger equation using this wave function considering first region I, between the barriers where V(x) = 0 and then region II, the barrier region where V(x) = V0:
In region I, Schrödinger's equation becomes:
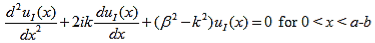(1)
With
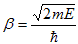 | (2) |
While in region II, it becomes: |
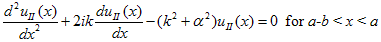 | (3) |
With |
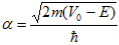 | (4) |
The solution to equations (1) and (4) are of the form: |
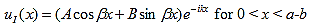 | (5) |
 | (6) |
Since the potential, V(x), is finite everywhere, the solutions for uI (x) and uII (x) must be continuous as well as their first derivatives. Continuity at x = 0 results in:
 | (7) |
And continuity at x = a-b combined with the requirement that u(x) be periodic:
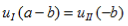 | (8) |
Results in: |
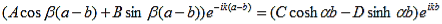 | (9) |
Continuity of the first derivative at x = 0 requires that: |
 | (10) |
The first derivatives of uI(x) and uII(x) are: |
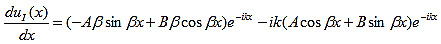 | (11) |
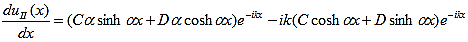 | (12) |
So that (10) becomes: |
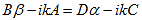 | (13) |
Finally, continuity of the first derivative at x = a-b, again combined with the requirement that u(x) is periodic, results in:
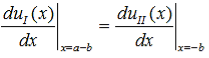 | (14) |
So that |
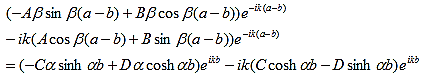(15)
This equation can be simplified using equation (9) to: |
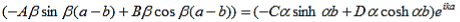 | (16) |
As a result we have four homogenous equations, (7), (9), (13), and (16), with four unknowns, A, B, C, and D, for which there will be a solution if the determinant of this set of equations is zero, or:
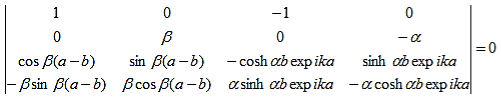 | (17) |
The first row of the determinant represents equation (7), the second row is obtained by combining (13) and (7), the third row represents equation (9) and the fourth row represents equation (16). This determinant can be rewritten as two determinants, each with three rows and columns, while replacing cosb(a-b) by bc, sinb(a-b) by bs, coshab eika by ac and sinhab eika by as, which results in:
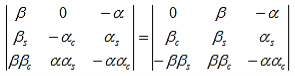(18)
Working out the determinants and using bc2 + bs2 = 1, and ac2 - as2 = e2ika, one finds: |
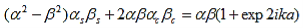 | (19) |
And finally, substituting bc, bs, ac and as: |
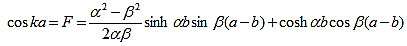 | (20) |
Where eika + e-ika was replaced by 2coska. Since the result is independent of the sign of k, this equation also covers all solutions obtained when replacing e-ik by eik in equations (5) and (6).
A further simplification is obtained as the barrier width, b, is reduced to zero while the barrier height, V0, is increased to infinity in such manner that the product, bV0, remains constant and the potential becomes a delta function train at x = a and repeated with a period of a, namely bV0 (x - b - na) where n is an integer. As b approaches zero, sinh b approaches b. Equation (20) then reduces to:
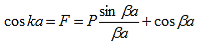 | (21) |
With |
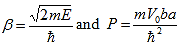 | (22) |
The right hand side of equation (21) shows the relation between the energy (through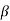 
) and the wave-vector, k, and as you can see, since the left hand side of the equation can only range from −1 to 1 then there are some limits on the values that 
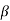(and thus, the energy) can take, that is, at some ranges of values of the energy, there is no solution according to these equation, and thus, the system will not have those energies: energy gaps. These are the so-called band-gaps, which can be shown to exist in any shape of periodic potential (not just delta or square barriers). This has been plotted in Figure.
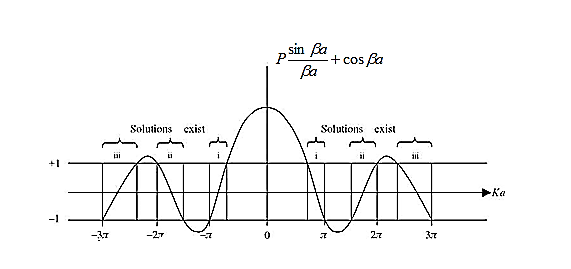
Figure 13: Graph of the right-hand side of equation (21) of P for P =2
- The permissible limit of the term
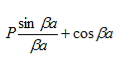
Lies between +1 to -1. By varying 
a, a wave mechanical nature could be plotted as shown in Figure, the shaded portion of the wave shows the bands of allowed energy with the forbidden region as unshaded portion.
Figure 14
2. With increase of 
a, the allowed energy states for a electron increases there by increasing the band width of the bands, i.e., the strength of the potential barrier diminishes. This also leads to increase of the distance between electrons and the total energy possessed by the individual electron.
3.Conversly if suppose the effect of potential barrier dominate i.e., if P is large, the resultant wave obtained in terms of shows a stepper variation in the region lies between +1 to -1. This results in the decrease of allowed energy and increase of forbidden energy gap. Thus, at extremities.
Case (i) when P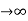
, the allowed energy states are compressed to a line spectrum.
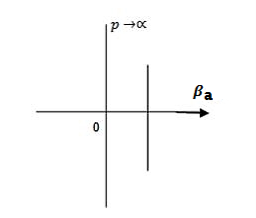
Figure 15
Case (ii) when P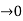
the energy band is broadened and it is quasi continuous
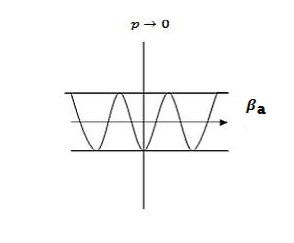
Figure 16
The electron energy forms quasi-continuous bands (because k itself is quasi-continuous) separated from each other by a minimum gap that occurs at ka= s(s = 0, ±1, ±2, ), or k= s/a, at which the left-hand side of Equation (21) is ±1. Figure 17 (b) implies that there are multiple values of k for each E. However, the Bloch theorem says that wave functions corresponding to the wave vectors k separated by m(2/a) (since b= 0) are identical, they are the same quantum state and should be counted only once. Thus, rather than plotting the energy eigenvalues for all the wave vectors, we can plot them in one period, as shown in Figure 18. This way of representation is called the reduced-zone representation. The relationship between the energy and the wave vector is the dispersion relation.
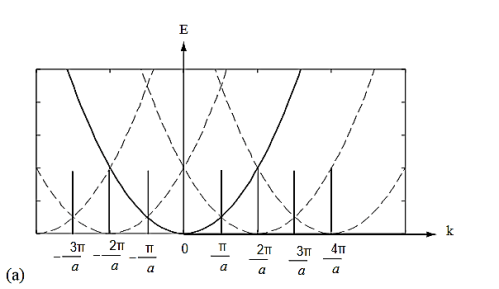
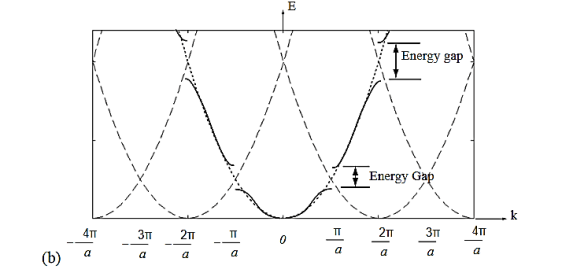
Figure 17
Figure 17 (a) Parabolic energy curves of a free electron in one dimension, periodically continued in reciprocal space. The periodicity in real space is a, and (b) extended zone: splitting of the energy parabola at the boundaries of the first Brillouin zone. The energy gaps are forbidden regions. The solid lines from Kronig-Penney model.
From the E-K diagram is clear that the electron has allowed energy values in the region or zone extending from k= -π/a to k= +π/a. This zone is called first Brillouin Zone. Higher zones can be defined accordingly from the graph.
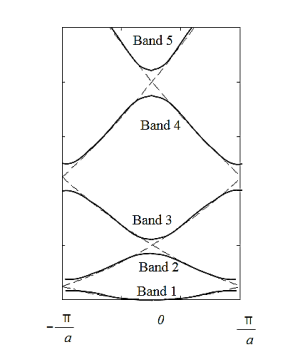
Figure 18: The solid lines show the energy bands in the reduced zone. The free electron dispersion relations are shown as dashed lines.
Consider an isolated silicon atom; its energy levels are quantized. When two identical atoms are brought closer together, the quantized energy levels hybridize and split into two different levels because of the mutual interaction of the two atoms. More generally, when N atoms are moved closer, until they reach the equilibrium inter-atomic distance d, the energy levels split into N levels. These N levels are very close to each other if N is large (which is the case in a crystal) so that they eventually form a continuous energy band.
Figure 19: Formation of Energy band as a function of interatomic distance (distance between atoms)
E-K DIAGRAM
The corresponding band structure is shown below (black curve) as well as the energy for a free electron (gray curve). Three different forms are presented, namely the E(k) diagram, the E (k diagram combined with the reduced-zone diagram as well as the reduced-zone diagram only.
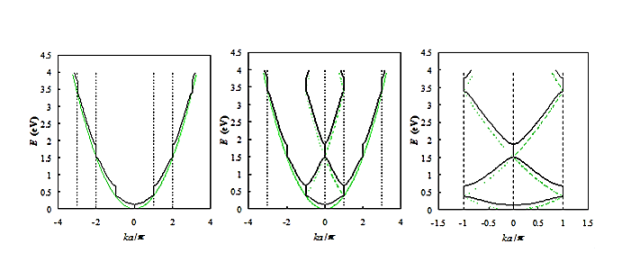
Figure 20: Energy versus ka/π as presented in Figure (black curves) compared to that of a free electron (gray curves). Shown are: a) the E(k) diagram, b) the E(k) diagram combined with the reduced-zone diagram and c) the reduced-zone diagram only.
From Figure 20 a we observe the following: The E(k) relation resembles a parabola except that only specific ranges of energies are valid solutions to Schrödinger's equation and therefore are allowed, while others are not. The range of energies for which there is no solution is referred to as an energy band gap. The transitions between allowed and forbidden energies occur at non-zero integer multiples of ka/ π. These correspond to local minima and maxima of the E(k) relation. The reduced-zone diagram shown in Figure 20 contains the first three bands and energy band gaps. For instance, the second energy bandgap occurs between 1.5 and 2 eV, between the band maximum of the second band and the band minimum of the third band.
