Unit-5
Bending & Torsion
Pure Bending of Beams
When a beam having an arbitrary cross section is subjected to a transverse loads the beam will bend. In addition to bending the other effects such as twisting and buckling may occur, and to investigate a problem that includes all the combined effects of bending, twisting and buckling could become a complicated one. Thus we are interested to investigate the bending effects alone, in order to do so, we have to put certain constraints on the geometry of the beam and the manner of loading.
Assumptions:
The constraints put on the geometry would form the assumptions:
1. Beam is initially straight and has a constant cross-section.
2. Beam is made of homogeneous material and the beam has a longitudinal plane of symmetry.
3. Resultant of the applied loads lies in the plane of symmetry.
4. The geometry of the overall member is such that bending not buckling is the primary cause of failure.
5. Elastic limit is nowhere exceeded and ‘E' is same in tension and compression.
6. Plane cross - sections remains plane before and after bending.

Let us consider a beam initially unstressed as shown in fig 1(a). Now the beam is subjected to a constant bending moment (i.e. ‘Zero Shearing Force') along its length as would be obtained by applying equal couples at each end. The beam will bend to the radius R as shown in Fig 1(b)
As a result of this bending, the top fibers of the beam will be subjected to tension and the bottom to compression it is reasonable to suppose, therefore, that some where between the two there are points at which the stress is zero.
The locus of all such points is known as neutral axis . The radius of curvature R is then measured to this axis. For symmetrical sections the N. A. Is the axis of symmetry but whatever the section N. A. Will always pass through the centre of the area or centroid.
The above restrictions have been taken so as to eliminate the possibility of 'twisting' of the beam.
Concept of pure bending:
Loading restrictions:
As we are aware of the fact internal reactions developed on any cross-section of a beam may consists of a resultant normal force, a resultant shear force and a resultant couple. In order to ensure that the bending effects alone are investigated, we shall put a constraint on the loading such that the resultant normal and the resultant shear forces are zero on any cross-section perpendicular to the longitudinal axis of the member,
That means F = 0

Thus, the zero shear force means that the bending moment is constant or the bending is same at every cross-section of the beam. Such a situation may be visualized or envisaged when the beam or some portion of the beam, as been loaded only by pure couples at its ends. It must be recalled that the couples are assumed to be loaded in the plane of symmetry.
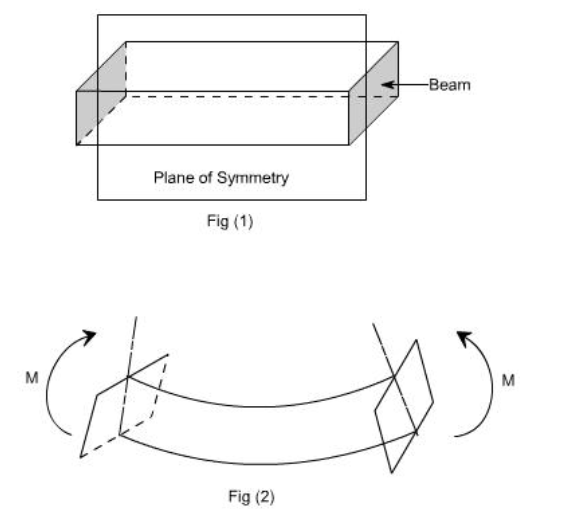
When a member is loaded in such a fashion it is said to be in pure bending. The examples of pure bending have been indicated in EX 1and EX 2 as shown below :
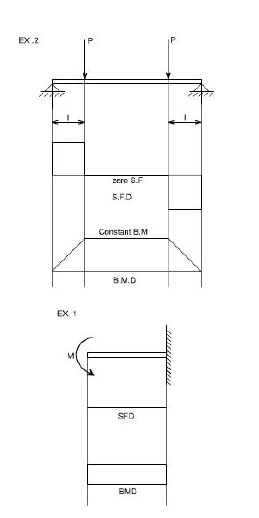
When a beam is subjected to pure bending are loaded by the couples at the ends, certain cross-section gets deformed and we shall have to make out the conclusion that,
1. Plane sections originally perpendicular to longitudinal axis of the beam remain plane and perpendicular to the longitudinal axis even after bending , i.e. the cross-section A'E', B'F' ( refer Fig 1(a) ) do not get warped or curved.
2. In the deformed section, the planes of this cross-section have a common intersection i.e. any time originally parallel to the longitudinal axis of the beam becomes an arc of circle.
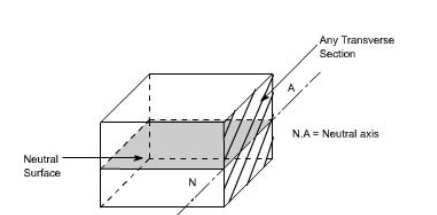
We know that when a beam is under bending the fibres at the top will be lengthened while at the bottom will be shortened provided the bending moment M acts at the ends. In between these there are some fibres which remain unchanged in length that is they are not strained, that is they do not carry any stress. The plane containing such fibres is called neutral surface.
The line of intersection between the neutral surface and the transverse exploratory section is called the neutral axisNeutral axis (N A) .
Bending Stresses in Beams or Derivation of Elastic Flexural formula :
In order to compute the value of bending stresses developed in a loaded beam, let us consider the two cross-sections of a beam HE and GF , originally parallel as shown in fig 1(a).when the beam is to bend it is assumed that these sections remain parallel i.e. H'E' and G'F' , the final position of the sections, are still straight lines, they then subtend some angle θ.
Consider now fiber AB in the material, at a distance y from the N.A, when the beam bends this will stretch to A'B'
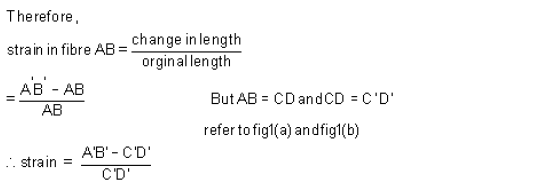
Since CD and C'D' are on the neutral axis and it is assumed that the Stress on the neutral axis zero. Therefore, there won't be any strain on the neutral axis.

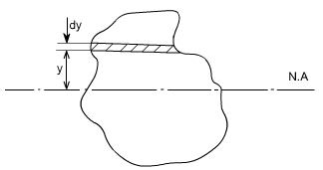
Consider any arbitrary a cross-section of beam, as shown above now the strain on a fibre at a distance ‘y' from the N.A, is given by the expression.


This equation is known as the Bending Theory Equation.The above proof has involved the assumption of pure bending without any shear force being present. Therefore this termed as the pure bending equation. This equation gives distribution of stresses which are normal to cross-section i.e. in x-direction.
Section Modulus:
From simple bending theory equation, the maximum stress obtained in any cross-section is given as
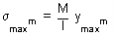
For any given allowable stress the maximum moment which can be accepted by a particular shape of cross-section is therefore
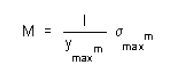
For ready comparison of the strength of various beam cross-section this relationship is some times written in the form.
 Is termed as section modulus.
Is termed as section modulus.
The higher value of Z for a particular cross-section, the higher the bending moment which it can withstand for a given maximum stress.
Beam : loads acting transversely to the longitudinal axis the loads create shear forces and bending moments, stresses and strains due to V and M are discussed in this chapter lateral loads acting on a beam cause the beam to bend, thereby deforming the axis of the beam into curve line, this is known as the deflection curve of the beam.
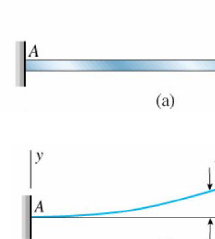
The beams are assumed to be symmetric about x-y plane, i.e. y-axis is an axis of symmetric of the cross section, all loads are assumed to act inthe x-y plane, then the bending deflection occurs in the same plane, it is known as the plane of bending the deflection of the beam is the displacement of that point from its original position, measured in y direction
Pure bending:
M = constant V = dM / dx = 0
Pure bending in simple beam and cantilever beam are shown
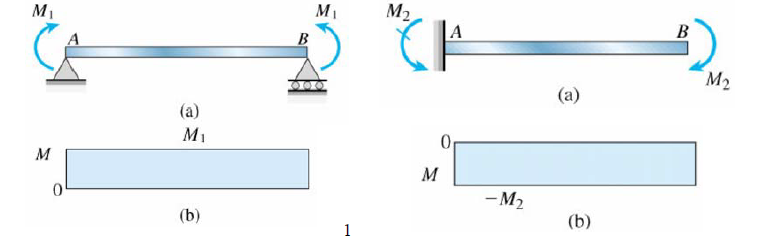
Non uniform bending:
M ≠ constant
V = dM / dx ≠ 0
Simple beam with central region in pure bending and end regions in non-uniform bending is shown
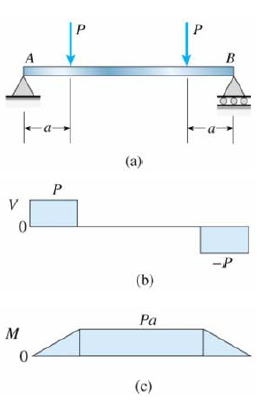
Curvature of a Beam
Consider a cantilever beam subjected to a load P
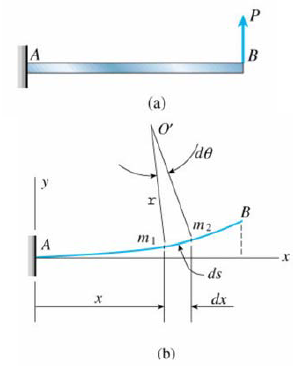
Choose 2 points m1 and m2 on the deflection curve, their normal intersect at point O', is called the centreof curvature, the distance m1O' is called radius of curvature ρ, and the curvature Kis defined as
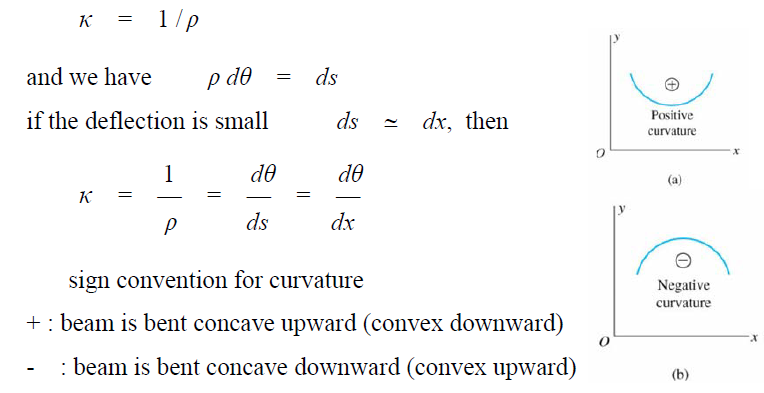
Longitudinal Strains in Beams
Consider a portion abof a beam in pure bending produced by a positive bending moment M, the cross section may be of any shape provided it is symmetric about y-axis under the moment M, its axis is bent into a circular curve, cross section mn and pq remain plane and normal to longitudinal lines (plane remains plane can be established by experimental result)
The symmetry of the beam and loading, it requires that all elements of the beam deform in an identical manner (∴the curve is circular), this are valid for any material (elastic or inelastic) due to bending deformation, cross sections mn and pq rotate w.r.t. Each other about axes perpendicular to the xy plane longitudinal lines on the convex (lower) side (nq) are elongated, and on the concave (upper) side (mp) are shortened the surface ss in which longitudinal lines do not change in length is called the neutral surface, its intersection with the cross-sectional plane is called neutral axis, for instance, the z axis is the neutral axis of the cross section
In the deformed elementρthe distance from O' to N.S. (or N.A.), thus ρdθ= dx

In the y and z directions because of the effects of Poisson's ratio.
Normal Stress in Beams (Linear Elastic Materials)
∵e x occurs due to bending, ∴the longitudinal line of the beam is subjected only to tension or compression, if the material is linear elastic
Then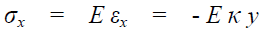
σvary linear with distance y from the neutral surfaceconsider a positive bendingmoment M applied, stresses arepositive below N.S. And negativeabove N.S.
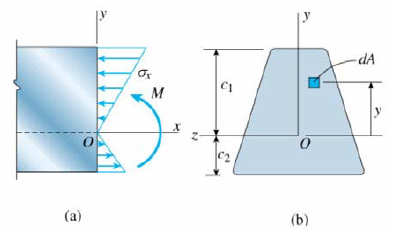
∵No axial force acts on the cross section, the only resultant is M, thus two equations must satisfy for static equilibrium condition.
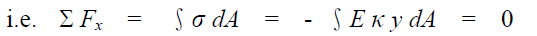
E and Kare constants at the cross section, thus we have∫y dA = 0
We conclude that the neutral axis passes through the controid of the cross section, also for the symmetrical condition in y axis, the y axis must pass through the centroid, hence, the origin of coordinates O is located at the centroid of the cross section the moment resultant of stress  is
is


This is called the flexure formula; the stress σx is called bending stresses or flexural stresses.

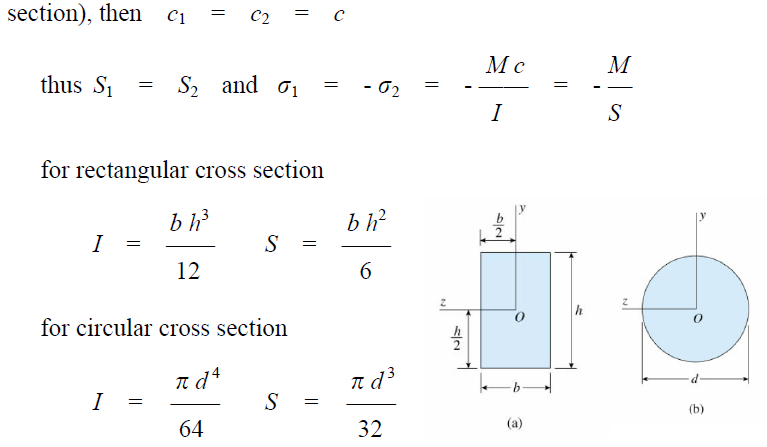
The preceding analysis of normal stress in beams concerned pure bending,No shear force in the case of non-uniform bending (V≠0), shear force produces warping (out of plane distortion), plane section no longer remain plane after bending, but the normal stress σx calculated from the flexure formula are not significantly altered by the presence of shear force and warping we may justifiably use the theory of pure bending for calculating σx even when we have non-uniform bending the flexure formula gives results in the beam where the stress distributionis not disrupted by irregularities in the shape, or by discontinuous in loading (otherwise, stress concentration occurs).
Torsion
Torsion of circular shafts Definition of Torsion: Consider a shaft rigidly clamped at one end and twisted at the other end by a torque T = F.d applied in a plane perpendicular to the axis of the bar such a shaft is said to be in torsion.
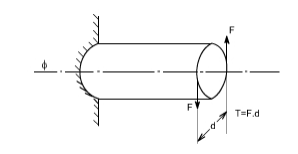
Effects of Torsion: The effects of a torsional load applied to a bar are
(i) To impart an angular displacement of one end cross – section with respect to the other end.
(ii) To setup shear stresses on any cross section of the bar perpendicular to its axis.
Assumption:
(i) The materiel is homogenous i.e of uniform elastic properties exists throughout the material.
(ii) The material is elastic, follows Hook's law, with shear stress proportional to shear strain.
(iii) The stress does not exceed the elastic limit.
(iv) The circular section remains circular
(v) Cross section remains plane.
(vi) Cross section rotates as if rigid i.e. every diameter rotates through the same angle.
Consider now the solid circular shaft of radius R subjected to a torque T at one end, the other end being fixed Under the action of this torque a radial line at the free end of the shaft twists through an angle θ, point A moves to B, and AB subtends an angle ‘ γ' at the fixed end. This is then the angle of distortion of the shaft i.e the shear strain.
Since angle in radius = arc / Radius
Arc AB = Rθ
= L γ [since L and γ also constitute the arc AB]
Thus, γ= Rθ / L (1)
From the definition of Modulus of rigidity or Modulus of elasticity in shear

When a shaft is subjected to a torque or twisting a shearing stress is produced in the shaft. The shear stress varies from zero in the axis to a maximum at the outside surface of the shaft.
The shear stress in a solid circular shaft in a given position can be expressed as:
τ = T r / J (1)
Where
τ = shear stress (Pa, lbf/ft2 (psf))
T = twisting moment (Nm, lbf ft)
r = distance from centre to stressed surface in the given position (m, ft)
J = Polar Moment of Inertia of Area (m4, ft4)
Circular Shaft and Maximum Moment or Torque
Maximum moment in a circular shaft can be expressed as:
Tmax = τmax J / R (2)
Where
Tmax = maximum twisting torque (Nm, lbf ft)
τmax = maximum shear stress (Pa, lbf/ft2)
R = radius of shaft (m, ft)
Combining (2) and (3) for a solid shaft
Tmax = (π / 16) τmax D3 (2b)
Combining (2) and (3b) for a hollow shaft
Tmax = (π / 16) τmax (D4 - d4) / D (2c)
Circular Shaft and Polar Moment of Inertia
Polar Moment of Inertia of a circular solid shaft can be expressed as
J = π R4 / 2
= π (D / 2)4 / 2
= π D4 / 32 (3)
Where
D = shaft outside diameter (m, in)
Polar Moment of Inertia of a circular hollow shaft can be expressed as
J = π (D4 - d4) / 32 (3b)
Where
d = shaft inside diameter (m, ft)
Diameter of a Solid Shaft
Diameter of a solid shaft can calculated by the formula
D = 1.72 (Tmax / τmax)1/3 (4)
Torsional Deflection of Shaft
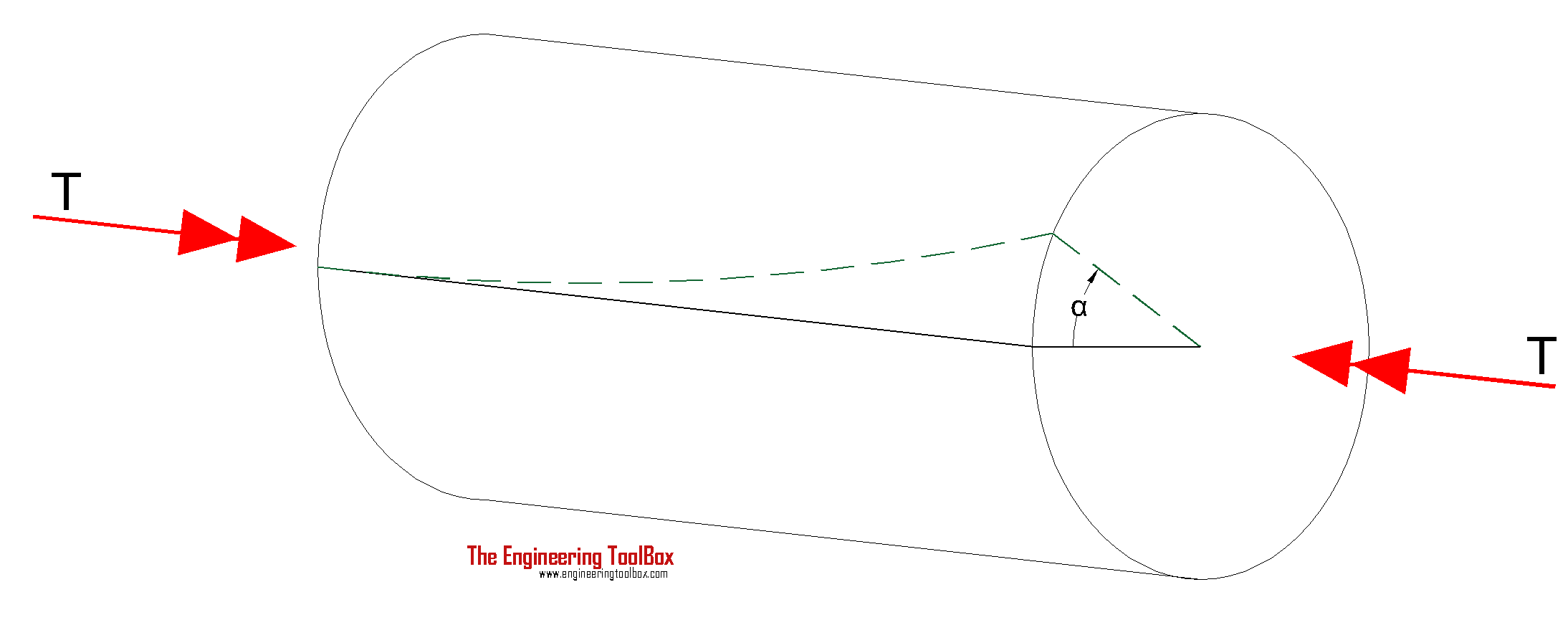
The angular deflection of a torsion shaft can be expressed as
α = L T / (J G) (5)
Where
α = angular shaft deflection (radians)
L = length of shaft (m, ft)
G = Shear Modulus of Rigidity - or Modulus of Rigidity (Pa, psf)
The angular deflection of a torsion solid shaft can be expressed as
α = 32 L T / (G π D4) (5a)
The angular deflection of a torsion hollow shaft can be expressed as
α = 32 L T / (G π (D4- d4)) (5b)
The angle in degrees can be achieved by multiplying the angle θ in radians with 180 / π.
Solid shaft (π replaced)
αdegrees ≈ 584 L T / (G D4) (6a)
Hollow shaft (π replaced)
αdegrees ≈ 584 L T / (G (D4- d4) (6b)
Torsion Resisting Moments from Shafts of Various Cross Sections
Shaft Cross Section Area | Maximum Torsional | Nomenclature | |
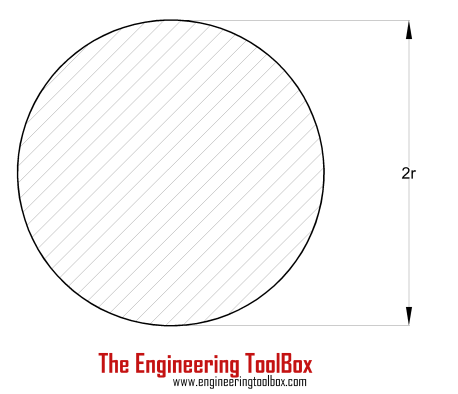 | Solid Cylinder Shaft | (π / 16) τmax (2 r)3 = (π / 16) τmax D3 |
|
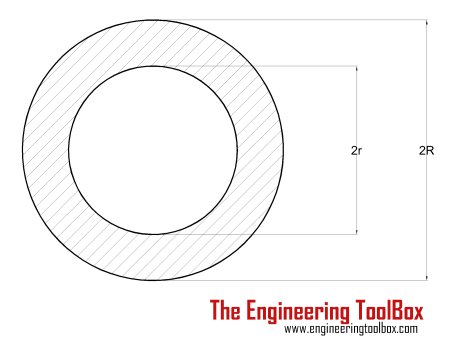 | Hollow Cylinder Shaft | (π / 16) τmax ((2 R)4 - (2 r)4) / (2 R) = (π / 16) τmax (D4 - d4) / D |
|
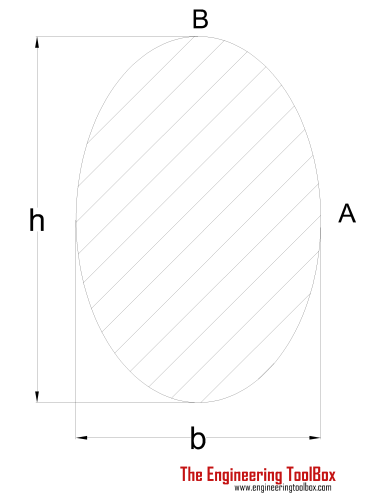 | Ellipse Shaft | (π / 16) τmax b2 h | h = "height" of shaft |
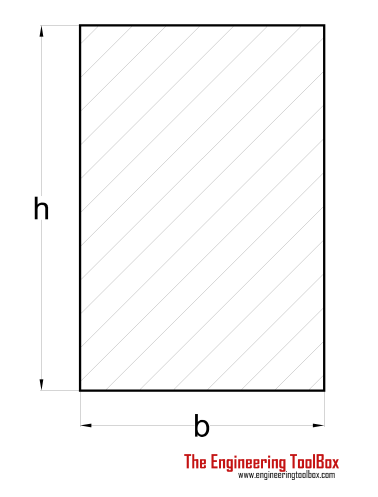 | Rectangle Shaft | (2 / 9) τmax b2 h | h > b |
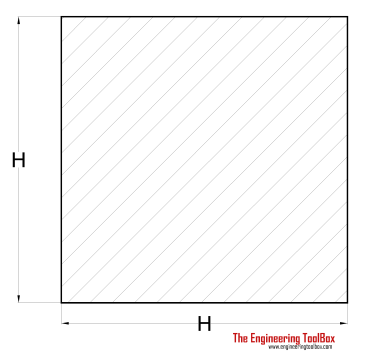 | Square Shaft | (2 / 9) τmax H3 |
|
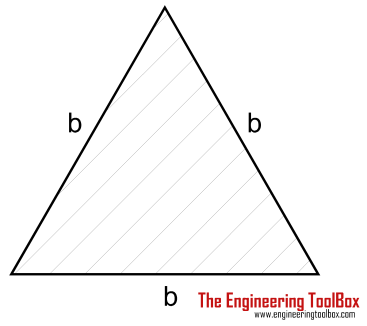 | Triangle Shaft | (1 / 20) τmax b3 | b = length of triangle side |
 | Hexagon Shaft | 0.123 τmax D3 |
|