Unit-1
Functions of One Real Variable
Let f be a differentiable function on an interval I. Then the derivative f′ is a function of x and if f′ is differentiable at x, then the derivative of f′ at x is called second derivative of f at x. It is denoted by f″(x) or f(2)(x).similarly, if f” is differentialble at x , then this derivative is called the 3rd derivative of f and it is denoted by f(3)(x). Proceeding in this way the nth derivative of f is the derivative of the function f(n-1)(x) and it the denoted by f(n)(x).
If y = f(x) then f(n) (x) is denoted by dn y/ dxn or Dn y or yn or yn and
F(n) (x)= lim h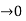 f(n-1) (x+h) – f(n-1) (x )/ h
f(n-1) (x+h) – f(n-1) (x )/ h
Successive nth derivative of elementary functions ie., trigonometric
Find the nth derivative of sin3 x
Sol: we know that sin 3x= 3sin x 4sin3 x = sin3x = 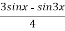
Differentiate n times w.r.t x,
dn/dxn ( sin3 x) = 1/4 dn/dxn (3 sinx- sin3x)
=1/4 ( -3n. Sin( 3x+ nπ/2) + 3 sin (x+ nπ/2)) nϵz
Example 2:
Find the nth derivative of sin 5x. Sin 3x.?
Sol: let y = sin 5x.sin 3x= 1/ 2( sin 5x.sin 3x)
⇒y= ½( cos 2x - cos8x)
⇒ y= ½ ( cos 2x- cos8x )
Differentiate n times w.r.t x,
Yn = ½ (dn/dxn) ( cos 2x - cos8x )
⇒ yn = ½ ( 2 n (cos( 2x+ nπ/2)- 8n .cos (8x + nπ/2)) nϵz.
Successive n th derivative of nth elementary function ie., exponential
If y = ae n x + be –nx , then show that y2= n2y
Sol: Y= aenx + be-nx
y 1 = a.n.enx - b.n.e-nx
y2 = an2 enx – bn2 e-nx = n2 (ae nx+ be –nx)
y2= n2y.
Example 2:
If y= e-kx/2(a cosnx+ b sinnx) then show that.,y2+ ky1+(n2+ k2/4)y =0
Sol : y= e-kx/2(a cosnx+ b sinnx)
Differentiating w.r.to. x.,
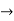 Y1 = e-kx/2( -an sin nx + bn cos nx) - k/2.y
Y1 = e-kx/2( -an sin nx + bn cos nx) - k/2.y

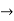 Y1+ k/2.y = ne-kx/2 ( -an sin nx + bn cos nx) (1)
Y1+ k/2.y = ne-kx/2 ( -an sin nx + bn cos nx) (1)
Differentiating w.r.to x.,
Y2+ k/2.y1 = ne-kx/2 (-k/2) ( -an sin nx + bn cos nx) + n e-kx/2(-an cosnx- bn sinnx).
= -(k/2) (y1+ k/2 y)- n2 y = - (k/2 y1)- ( k2/4)y- n2y.
 y2 + ky1 +(n2+ k2/4)y = 0.
y2 + ky1 +(n2+ k2/4)y = 0.
Successive differentiation of nth derivative of elementary functions ie., logarithmic
Example :
If Y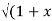 2) = log( x +
2) = log( x + 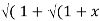 2) ) then show that (1 + x 2) y1 +xy =1
2) ) then show that (1 + x 2) y1 +xy =1
Sol: Y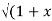 2) = log( x +
2) = log( x + 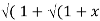 2) )
2) )
Differentiating w.r.to x.,
y.1/ 2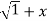 2 .2x+
2 .2x+ 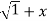 2. Y1.
2. Y1.
=(1+x ) y +xy = 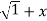 . 1/x+
. 1/x+ 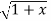 2 .
2 .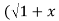 2) +x/
2) +x/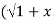 2 =1
2 =1
In mathematical analysis, the alternating series test is the method used to prove that an alternating series with terms that decrease in absolute value is a convergent series. The test was used by Gottfried Leibniz and is sometimes known as Leibniz's test, Leibniz's rule, or the Leibniz criterion.
Leibnitz test is an alternative way of expressing derivatives to f’(x),g’(x),etc.,
If y is expressed in terms of x then the derivative is written as 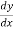
Example 1:
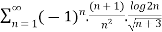
Solution:
It is an alternating series ,with
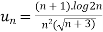 here (-1)n defines only the sign
here (-1)n defines only the sign
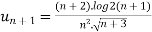
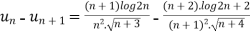
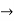
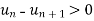 for all n
for all n

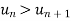
Now,
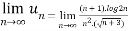
=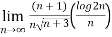
=0 as 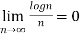
Hence by Leibnitz’s rule of alternating series 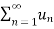 is converging.
is converging.
Example 2:
Q = 9R2-  to find
to find 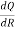
Solution:
Q = 9R2-15R-3
Now,
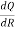 = 18R+45R-2 = 18R +
= 18R+45R-2 = 18R +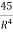
Power series:
A power series can be written in the form of
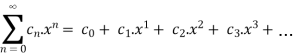
It can be written in the form of a function as.,
f(x) =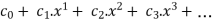
If we let  =1 for all n then the power series tends to geometric series
=1 for all n then the power series tends to geometric series
f(x) = 1+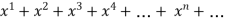
The above series converges if -1<x<1
The above series diverges if x≥ 1 and x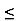 -1
-1
Example 3:
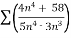 n
n
L= 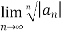 =
= 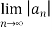 1/n
1/n
L= 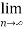
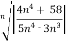 n =
n =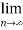

=  <1
<1
Hence the series converges.
For the theorem in harmonic function theory, see Harmonic function § The mean value property.
In mathematics, the mean value theorem states, roughly, that for a given planar arc between two endpoints, there is at least one point at which the tangent to the arc is parallel to the secant through its endpoints.
This theorem is used to prove statements about a function on an interval starting from local hypotheses about derivatives at points of the interval.
More precisely, if f is a continuous function on the closed interval [a,b] and differentiable on the open interval (a,b), then there exists a point c in (a,b) such that the tangent at c is parallel to the secant line through the endpoints (a,f(a)) and (b,f(b)) that is,
f’(c) = 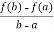

It is one of the most important results in real analysis.
Formal statement:
Let f:[a,b]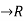 be a continuous function on the closed interval [a ,b] and differentiable on the open interval (a,b) where a<b. Then there exists some c in (a,b) such that
be a continuous function on the closed interval [a ,b] and differentiable on the open interval (a,b) where a<b. Then there exists some c in (a,b) such that
f’(c) = 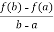
The mean value theorem is a generalization of Rolle's theorem, which assumes f(a)= f(b), so that the right-hand side above is zero.
The mean value theorem is still valid in a slightly more general setting. One only needs to assume that f:[a,b]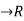 is continuous on [a,b] , and that for every x in (a,b) the limit
is continuous on [a,b] , and that for every x in (a,b) the limit
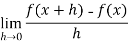
Exists as a finite number or equals  . If finite, that limit equals f’(x) . An example where this version of the theorem applies is given by
. If finite, that limit equals f’(x) . An example where this version of the theorem applies is given by
The real valued cube root function mapping x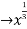 , whose derivative tends to infinity at the origin.
, whose derivative tends to infinity at the origin.
Note that the theorem, as stated, is false if a differentiable function is complex-valued instead of real-valued. For example, define f(x)=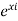 for all real x . Then
for all real x . Then
f(2 )-f(0)=0=0(2
)-f(0)=0=0(2
while f’(x) ≠ 0 for any real x .
These formal statements are also known as Lagrange's Mean Value Theorem.
Proof:
The expression 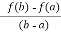 gives the slope of the line joining the points (a, f(a)) and
gives the slope of the line joining the points (a, f(a)) and
(b, f(b)) , which is a chord of the graph of f , while f’(x) gives the slope of the tangent to the curve at the point (x,f(x)) . Thus the mean value theorem says that given any chord of a smooth curve, we can find a point lying between the end-points of the chord such that the tangent at that point is parallel to the chord. The following proof illustrates this idea.
Define g(x)=f(x)-rx , where r is a constant. Since f is continuous on [a,b] and differentiable on (a,b) , the same is true for g . We now want to choose r so that g satisfies the conditions of Role’s theorem. Namely
 g(a) = g(b) f(a) – ra=f(b)-rb
g(a) = g(b) f(a) – ra=f(b)-rb
r(b-a)=f(b)-f(a)
 r=
r=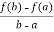
By Role’s theorem, since g is differentiable and g(a)=g(b) , there is some c in (a,b) for which g’(c) = 0 , and it follows from the equality g(x)=f(x)-rx that,
g’(x) =f(x)-r
 g’(c) = 0
g’(c) = 0
 g’(c) = r=
g’(c) = r=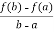
Cauchy's mean value theorem, also known as the extended mean value theorem, is a generalization of the mean value theorem. It states: If functions f and g are both continuous on the closed interval [a, b], and differentiable on the open interval (a, b), then there exists some c ∈ (a, b), such that
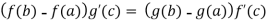
Of course, if g((a)≠g(b) and if g’(c)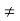 0,this is equivalent to:
0,this is equivalent to:

Geometrical meaning of Cauchy's theorem
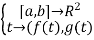
Which is parallel to the line defined by the points (f(a), g(a)) and (f(b), g(b)). However Cauchy's theorem does not claim the existence of such a tangent in all cases where (f(a), g(a)) and (f(b), g(b)) are distinct points, since it might be satisfied only for some value c with f′(c) = g′(c) = 0, in other words a value for which the mentioned curve is stationary; in such points no tangent to the curve is likely to be defined at all. An example of this situation is the curve given by
t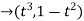
Which on the interval [−1, 1] goes from the point (−1, 0) to (1, 0), yet never has a horizontal tangent; however it has a stationary point (in fact a cusp) at t = 0.
Cauchy's mean value theorem can be used to prove l'Hôpital's rule. The mean value theorem is the special case of Cauchy's mean value theorem when g(t) = t.
Proof of Cauchy's mean value theorem:
The proof of Cauchy's mean value theorem is based on the same idea as the proof of the mean value theorem.
Suppose g(a) ≠ g(b). Define h(x) = f(x) – rg (x), where r is fixed in such a way that
h(a) = h(b), namely
h(a)=h(b) 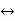 f(a)-rg(a) = f(b)-rg(b)
f(a)-rg(a) = f(b)-rg(b)
 r
r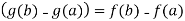
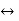 r=
r=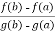
Since f and g are continuous on [a, b] and differentiable on (a, b), the same is true for h. All in all, h satisfies the conditions of Role’s Theorem consequently, there is some c in (a, b) for which h′(c) = 0. Now using the definition of h we have:
0 = h’(c) =f’(c)-r.g’(c) = f’(c) – 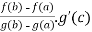
Therefore:
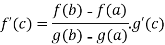
Which implies the result
If g (a) = g (b), then, applying Role’s theorem to g, it follows that there exists c in (a, b) for which g′(c) = 0. Using this choice of c, Cauchy's mean value theorem (trivially) holds.
Mean value theorem in several variables:
The mean value theorem generalizes to real functions of multiple variables. The trick is to use parameterization to create a real function of one variable, and then apply the one-variable theorem.
Let G be an open convex subset of  , and let f:G
, and let f:G be a differentiable function. Fix points x,y
be a differentiable function. Fix points x,y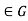 , and define g(t) = f((1-t)x+ty) . Since g is a differentiable function in one variable, the mean value theorem gives:
, and define g(t) = f((1-t)x+ty) . Since g is a differentiable function in one variable, the mean value theorem gives:
g(1) – g(0) = g’(c)
For some c between 0 and 1. But since g(1) = f(y) and g(0)= f(x) , computing g’(c) explicitly we have:
f(y) –f(x) =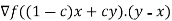
Where 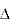 denotes a gradient and (
denotes a gradient and (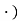 a dot product. Note that this is an exact analogue of the theorem in one variable (in the case n=1 this is the theorem in one variable). By the Cauchy–Schwarz inequality, the equation gives the estimate:
a dot product. Note that this is an exact analogue of the theorem in one variable (in the case n=1 this is the theorem in one variable). By the Cauchy–Schwarz inequality, the equation gives the estimate:
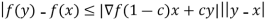
In particular, when the partial derivatives of f are bounded, f is Lipchitz continuous (and therefore uniformly continuous). Note that f is not assumed to be continuously differentiable or continuous on the closure of G . However, in order to use the chain rule to compute g’, we really do need to know that f is differentiable on G; the existence of the x and y partial derivatives by itself is not sufficient for the theorem to be true.
As an application of the above, we prove that f is constant if G is open and connected and every partial derivative of f is 0. Pick some point  , and let
, and let  g(x) = f(x) – f(x0). We want to show g(x)-0 for every x
g(x) = f(x) – f(x0). We want to show g(x)-0 for every x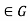 .
.
For that, let E- 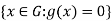 Then E is closed and nonempty. It is open too: for every x
Then E is closed and nonempty. It is open too: for every x ,
,
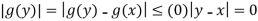
for every y in some neighbourhood of x . (Here, it is crucial that x and y are sufficiently close to each other.) Since G is connected, we conclude  .
.
The above arguments are made in a coordinate-free manner; hence, they generalize to the case when G is a subset of a Banach space.
Examples on mean value theorems:
Example 1:
Use lagranges mean value thorem to determnine a point P on the curve y=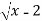 ,where the tangent is parallel to the chord joining (2,0) and (3,1).
,where the tangent is parallel to the chord joining (2,0) and (3,1).
Solution:
Consider y= in [2,3]....(1)
in [2,3]....(1)
(i)Function is continuous in[2,3] as algebraic expression with positive exponent is continuous
(ii)y’=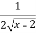 ,y’ exists in (2,3) hence the function is derivable in(2,3)
,y’ exists in (2,3) hence the function is derivable in(2,3)
Hence the conditions of LMV theorem are satisfied.
Hence thereexists, at least one c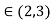 ,such that
,such that 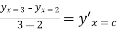
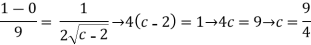
 For x=
For x= ,tangent is parallel to the chor joining(2,0) and (3,1)
,tangent is parallel to the chor joining(2,0) and (3,1)
By substituting in equation (1) we get ,
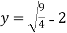 =
=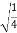 =
= 
Example 2:
Find the slope point on the graph y=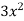 on[1,2] at which the tangent to the graph has the same slope as the line that passes through the end points (1,2) and (3,12)of the closed interval.
on[1,2] at which the tangent to the graph has the same slope as the line that passes through the end points (1,2) and (3,12)of the closed interval.
Solution:
Step 1: find the slope of the points that passes through the endpoints at
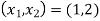
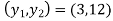
 the required slope is given by
the required slope is given by 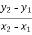 =
=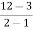 =9
=9
Step 2:
Find the point on the curve where the slope is 9
Y’=6x
6x=9 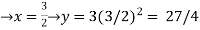
 the instantaneous rate of change of slope is 9
the instantaneous rate of change of slope is 9
Example 3:
Show that sinx<x for all x>0
Solution:
If x>2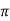 ,then sinx
,then sinx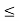 1<2
1<2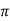 <x. If 0<x
<x. If 0<x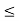 2
2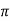 ,then by the mean value theorem,there-exists c in open interval(0,2
,then by the mean value theorem,there-exists c in open interval(0,2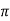 ) such that
) such that
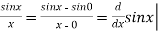 x=c = cosc<1
x=c = cosc<1
Thus,sinx<x in this case also.
Example 4:
Find the values of the c,which satisfy the equation 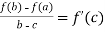 as stated in mean value theorem for the function f(x) =
as stated in mean value theorem for the function f(x) = in the interval [1,3]
in the interval [1,3]
Solution:
First let us check the mean value theorem conditions,
F(x) is continuous in its domain[0,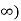 and hence the given interval [1,3]
and hence the given interval [1,3]
F(x) is also differentiable in the given interval .plugging a=1 and b=3 in the expression on the left side of the equation.
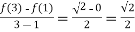
Now, the derivative of the function can be found using chain rule as
f’(x) =
Hence, the equation can be formed as
f’(c)= 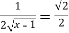
Cross multiplying and squaring the equation reduces to,
2(c-1)=1 which gives the solution as c=3/2 which lies in the interval [1,3].
Sequence and series is one of the basic topics in Arithmetic. An itemized collection of elements in which repetitions of any sort are allowed is known as a sequence, whereas series is the sum of all elements. An arithmetic progression is one of the common examples of sequence and series.
- In short, a sequence is a list of items/objects which have been arranged in a sequential way.
- A series can be highly generalized as the sum of all the terms in a sequence. However, there has to be a definite relationship between all the terms of the sequence.
The fundamentals could be better understood by solving problems based on the formulas. They are very similar to sets but the primary difference is that in a sequence, individual terms can occur repeatedly in various positions. The length of a sequence is equal to the number of terms and it can be either finite or infinite. This concept is explained in a detailed manner in Class 11 Maths. With the help of definition, formulas and examples we are going to discuss here the concepts of sequence as well as series.
Definition of Sequence
In mathematics, an ordered set of objects or numbers, like a1, a2, a3, a4, a5, a6……an…. are said to be in a sequence, if, as per certain rule, has a definite value. The members of the sequence are called term or element which is equal to any value of the natural number. Every term in a sequence is related to the preceding and succeeding term. In general, sequences have a hidden rules or pattern, which helps you find out the value of the next term.
The nth term is the function of integer n (positive), regarded as the general term of the sequence. A sequence can be finite or infinite.
- Finite Sequence: A finite sequence is one that stops at the end of the list of numbers a1, a2, a3, a4, a5, a6……an, is represented by:
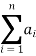
- Infinite Sequence: An infinite sequence refers to a sequence which is unending, a1, a2, a3, a4, a5, a6……an….., is represented by:
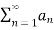
Definition of Series
The addition of the terms of a sequence (an), is known as series. Like sequence, series can also be finite or infinite, where a finite series is one that has a finite number of terms written as a1 + a2 + a3 + a4 + a5 + a6 + ……an. Unlike infinite series, where the number of elements are not finite or which are unending, written as a1 + a2 + a3 + a4 + a5 + a6 + ……an +….
If a1 + a2 + a3 + a4 + a5 + a6 + …… an = Sn, then Sn is considered as the sum to n elements of the series. The sum of terms is often represented by Greek letter sigma (Ʃ). Hence,
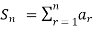
Example 1:
In a geometric progression, the second term is 12 and the sixth term is 192.find the eleventh term
Solution:
The required geometric progression is,
a+ar+ar2+ar3+.....
Given the second term is ar=12...(1)
Sixth term is ar5 = 192.....(2)
Dividing eq(2) by eq(1) we get ,
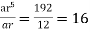
 r4 = 16
r4 = 16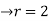
Substituting r in eq(1) we get ar=12/2=6
 eleventh term is given by ar10 = 6
eleventh term is given by ar10 = 6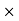 210 =6144
210 =6144
Example 2:
If sn denotes the sum of first n terms of an A.P and [s3n-sn-1]/[s2n-s2n-1]=31,then the value of n is
Solution:
S 3n = [3n / 2] [2a + (3n − 1) d]
Sn−1 = ([n − 1] / 2) * [2a + (n − 2) d]
⇒ S3n − Sn−1 = [1 / 2] [2a (3n − n + 1)] + [d / 2] [3n (3n − 1) − (n − 1) (n − 2)]
= [1 / 2] [2a (2n + 1) + d (8n2 − 2)]
= a (2n + 1) + d (4n2 − 1)
= (2n + 1) [a + (2n − 1) d]
S2n − S2n−1 = T2n = a +(2n − 1) d
⇒ S3n − Sn − S2n −S2n−1 = (2n + 1)
Given, ⇒ [S3n − Sn−1] / [S2n − S2n−1] = 31
⇒ n = 15
Example 3:
If Sn denotes the sum of first n terms of an A.P ,whose first term is 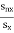 is independent of x,then SP =?
is independent of x,then SP =?
Solution:
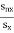 =
= 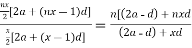
For 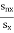 to be independent
to be independent
2a-d=0 or 2a=d
Now,
Sp = 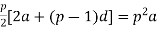
In mathematics, a series expansion is a method for calculating a function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and division). The resulting so-called series often can be limited to a finite number of terms, thus yielding an approximation of the function.
- Taylor series: power series based on a function’s derivatives at a single point.
- Maclaurin series: A special case of a Taylor series, centred at zero.
- Laurent series: An extension of the Taylor series, allowing negative exponent values.
- Dirichlet series: Used in number theory.
- Fourier series: Describes periodical functions as a series of sine and cosine functions. In acoustics, e.g., the fundamental tone and the overtones together form an example of a Fourier series.
- Newtonian series
- Legendre polynomials: Used in physics to describe an arbitrary electrical field as a superposition of a dipole field, a quadrupole field, an octupole field, etc.
- Zernike polynomials: Used in optics to calculate aberrations of optical systems. Each term in the series describes a particular type of aberration.
- Stirling series: Used as an approximation for factorials.
Examples of some expansion of series:
Example 1:
Taylor series:
The taylor’s series can be represented as the following
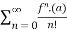 (x-a)n
(x-a)n
Example 1:
Find the taylor series for the following:
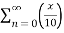
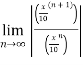 =
= 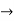
 <1
<1
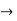 (x/10)<1 and (x/10) > -1
(x/10)<1 and (x/10) > -1
Therefore radius of convergence is (-10,10)
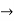 ROC =10
ROC =10
Example 2:
f(n)5 = 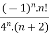
Here the ROC is 4
Maclaurian series:
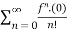 (x)n
(x)n
Example 3:
f(x)=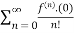

= f(0)+f’(0)x+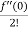 x2 +
x2 + 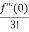 x3 +......
x3 +......
= 1+x+x2 +x3 + .....
= 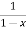
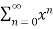
Let L is some finite positive number. Then the improper integrals of f and g with the same limits of integration behave the same way, ie either both converge or both diverge. Since this test for convergence of a basic-type improper integral makes use of a limit, it's called the limit comparison test , abbreviated as LCT.
An integral is said to be improper integral if the following condition is satisfied
Definite integral 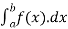 were required to have
were required to have
- A finite domain of integration [a,b]
- Finite integrand f(x) <
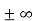
Example 1:
Solve the following improper integral 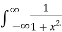 dx
dx
Solution:
By definition
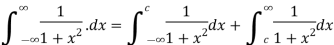
Here we consider at c=0
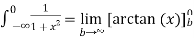 =
= 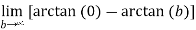
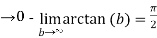
Here the integral converges at 
Example 2:
Find 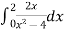
Solution:
The denominator of 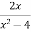 is 0 when x=2, so the function is not defined even when x=2.so,
is 0 when x=2, so the function is not defined even when x=2.so,
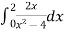 =
=
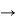
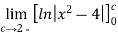 -ln(4) =-
-ln(4) =-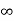
So the integral diverges