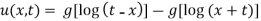Unit-2
FUNCTIONS OF SEVERAL VARIABLES:
Limit:
A limit is a number that a function approaches as the independent variable of the function approaches a given value. For example, given the function f (x) = 3x , you could say, “The limit of f (x) as x approaches 2 is 6 .” Symbolically, this is written 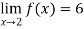 .
.
Continuity:
Continuity is another far-reaching concept in calculus. A function can either be continuous or discontinuous. One easy way to test for the continuity of a function is to see whether the graph of a function can be traced with a pen without lifting the pen from the paper. For the math that we are doing in pre calculus and calculus, a conceptual definition of continuity like this one is probably sufficient, but for higher math, a more technical definition is needed. Using limits, we’ll learn a better and far more precise way of defining continuity as well. With an understanding of the concepts of limits and continuity, you are ready for calculus.
Example 1:
Find the limit of the following points
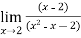
X | 1.9 | 1.99 | 1.999 | 2.001 | 2.01 | 2.1 |
F(x) |
|
|
|
|
|
|
Solution:
We apply the value of each x by finding the respective value through appliying limits
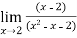
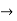 f(x)=
f(x)= 
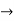 f(x)=
f(x)= 
Finding limit at x= 1.9
f(x)= 
f(1.9)=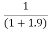
=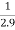
= 0.3448
Limit at x=1.99
f(1.99)= 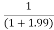
=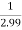
= 0.33444
Limit at x=1.999
f(1.999)= 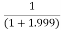
=
= 0.33344
Limit at x=2.001
f(2.001)= 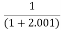
=
= 0.33322
Limit at x=2.01
f(2.01)= 
=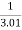
= 0.3225
From the above table we have to estimate the limit when x tends to 2
Here answer is 0.333....
Example 2:
Determine whether the following is dis-continuous at x=-1,0,

Solution :
Given 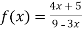
Verifying for continuity at x=-1

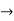
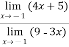
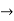
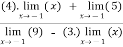
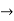
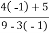
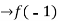
Therefore here 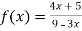 = f(-1)
= f(-1)
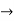 f(x)=f(-1)
f(x)=f(-1)
Hence the function is continuous at x=-1
Verifying at x=0
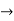

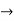
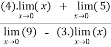
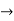
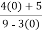
Therefore here 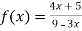 = f(0)
= f(0)
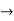 f(x)=f(0)
f(x)=f(0)
Hence the function is continuous at x=0
Example 3:
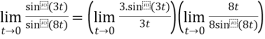
=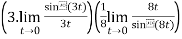
=(3)(
=
Partial Differentiation Partial differentiation is used to differentiate mathematical functions having more than one variable in them. In ordinary differentiation, we find derivative with respect to one variable only, as function contains only one variable. So partial differentiation is more general than ordinary differentiation.
Example 1:
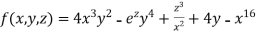
Solution:
Partial derivative for the given equation is,

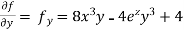


Example 2:
Find the partial derivative of the following
Z=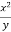 ,x=st , y=
,x=st , y=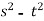
Solution:
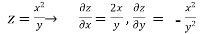
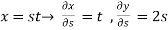

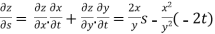

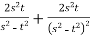 .
.
Example 3:
Solve the following D.E
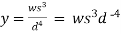
Solution :
Approximating over all change in y
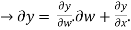
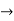
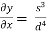 =
=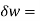 0.02w
0.02w 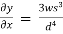 =
=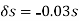
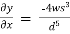 =
=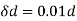
Substituting into equation we get,
 (-0.03s) +
(-0.03s) +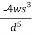 (0.01d) =0.11
(0.01d) =0.11 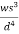
Therefore y decreases by approximately 11 percent.
The total derivative is the derivative with respect to of the function that depends on the variable not only directly but also via the intermediate variables . In mathematics, the total derivative of a function {display style f} at a point is the best linear approximation near this point of the function with respect to its arguments. Unlike partial derivatives, the total derivative approximates the function with respect to all of its arguments, not just a single one.
A(u) = f(x1,x2,.....) and u has continuous partial derivatives fx and fy. Here xi = xi(t) where i=0,1,2,3...n[ ]
]
Total derivative 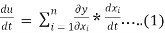
Eq(1) can be written in differential form by eliminating dt as,
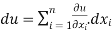
Example 1:
Suppose 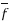 :
: 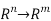 is given by
is given by
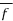 (
( = B
= B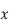 +
+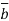 ,
,
Where B is an m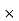 n –matrix and
n –matrix and 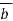

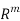 .For example if B=
.For example if B= 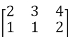 and
and 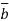 =
= 
f(x,y,z) = 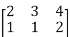
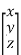 +
+ 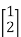 =
= 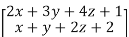
We claim that D.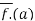 = B for all
= B for all 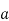 .to check this note
.to check this note
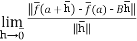
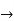
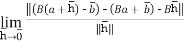
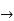
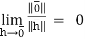
So indeed, D = B
= B
Example 2:
Find the total derivative of f(x,y)=2x+3y with respect to x,
Given that y= sin-1(x)
Solution:
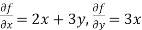
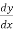 =
= 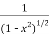
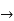
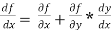
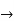 2x+3y+3x.
2x+3y+3x.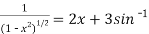 x +
x + 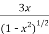
Example 3:
The radius and height of a cylinder are both 2cm.the radius is decreased at 1 cms and the height is increasing at 2 cms. What is the change in volume at this instant
The volume of a right circular cylinder is,
V=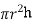
We are taking total derivative of this whole to get,
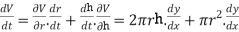
 2
2 (2)(2)(-1)+
(2)(2)(-1)+ = -8
= -8 +8
+8 =0
=0
At this moment, the volume of the cylinder is not changing.
Jacobian method:
Example 1:
Determine the jacobian matrix of the function
f: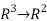 given by f(x,y,z)=(xy+2yz+2xy2z).
given by f(x,y,z)=(xy+2yz+2xy2z).
SOLUTION:
We first write f = f( where
where 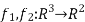 are given by the formulas
are given by the formulas 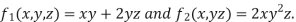 we know compute the gradients of these functions .we have that,
we know compute the gradients of these functions .we have that,
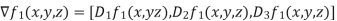
= [y,x+2z,2y]

= [2y2z,4xyz,2xy2]
The jacobian matrix f is therefore the 2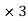 matrix whose first row is
matrix whose first row is 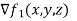 and the second row is
and the second row is 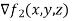 so
so
Df ( x ,y ,z) = 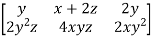
Example 3:
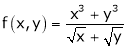
Consider 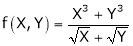
Put 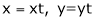
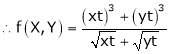
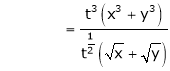
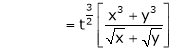
 .
.
Thus degree of f(x, y) is 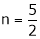
Note that
If  be a homogeneous function of degree n then z can be written as
be a homogeneous function of degree n then z can be written as
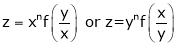
Beta and gamma are the two most popular functions in mathematics. Gamma is a single variable function, whereas Beta is a two-variable function. The relation between beta and gamma function will help to solve many problems in physics and mathematics. Beta And Gamma Function.
Example 1:
f(B) = 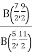 Solve the given function.
Solve the given function.
= 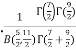
= 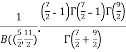 [Recursive function for the gamma function]
[Recursive function for the gamma function]
= 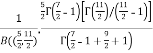 [Recursive formula for the gamma function]
[Recursive formula for the gamma function]
=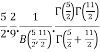
=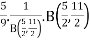 [By the definition of Beta function]
[By the definition of Beta function]
= 
Example 2:
B =
=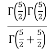
= 
= 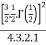
=
= 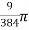 [because
[because 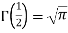
- Determine the image of a region under a given transformation of variables.
- Compute the Jacobian of a given transformation.
- Evaluate a double integral using a change of variables.
- Evaluate a triple integral using a change of variables.
Example 1:
Evaluate  . DA
. DA
Solution :
Here s is the region bounded by the lines on the real lines
X+ y=0; x+ y=-1
x- y=0 ; x-y = 8
Let
u=x+ y , 0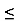 u
u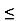 1
1
v=x-y , 0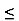 v
v 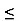 8
8
Now we have two choices
*solve for x and y if possible
*use the inverse transmission
- Solving for x and y
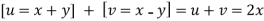
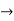
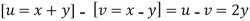
X=1/2(u)+1/2(v) and y =1/2(u-1/2(v)
Using of inverse method:
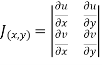 and
and 



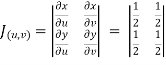
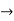
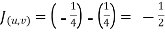
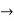
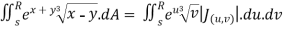
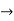

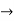
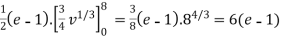

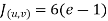
Example 2:
Evaluate 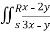 .dA
.dA
Solution:
Here s is the region bounded by the lines on the real lines
X - 2y=0; x - 2y= 4
3x-y=1 ;3 x-y = 8
Let
u=x – 2y
v= 3x- y
Now we have two choices
*solve for x and y if possible
*use the inverse transmission
Using of inverse method:
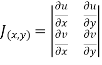 and
and 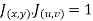

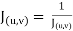
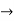
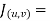
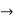 where
where  ,
, 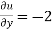 ,
, 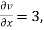
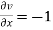
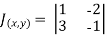 = -1+6 =5
= -1+6 =5
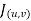 =
= 
Example 1:
Given a plane z= 3x+4y+2 that lies above the rectangle [0,5]  [1,4]. Find the surface area
[1,4]. Find the surface area
Solution:
The area of the surface with equation z=f(x,y),(x,y) D ,where
D ,where 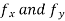 are continuous,
are continuous,
Is A(S)= 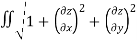 dA
dA
We have z=2+3x+4y.
Then, and
and 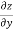 =4
=4
A(S) =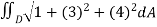
From the dimensions of the rectangle, we get the limits of x as (0,5) and the limits of y as(1,4)
On substituting the known values in the expression for area ,we get
A(S) =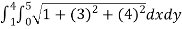
Evaluate the iterated integral.
A(S) =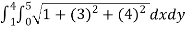
=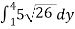
=15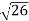
Example 2:
As an example, let us consider the following integral in two dimensions:
I=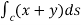
Where C is a straight line from the origin to (1,1), as shown the figure ,Let s be the arc length measured from the origin .We then have
x =s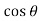 =
=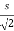
y=s sin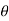 =
=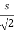
The endpoint (1,1) corresponds to s=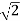 .Thus , the line integral becomes
.Thus , the line integral becomes
I=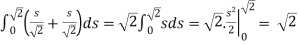
Required for Dirichlet’s integration:
f(t) = 
1.f(t) must be single valued everywhere
2.f(t) must have a finite number of discontinuities(must be finite) in one period
3.f(t) finite numbers of maxima and minima
4.the integral over one period < 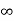
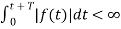 for all t
for all t
Example :
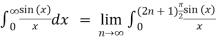
= 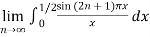 by substituting x
by substituting x (2n+1)
(2n+1)
= 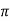 .
.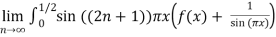
= 
= 
Example 2:
Consider the Dirichlet problem for the wave equation which describes a string attached between walls with one end attached permanently and with the other moving with the constant velocity ie. The d’Almbert equation on the triangular region of the Cartesian product of the space and the time.
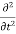 u(x,t)-
u(x,t)-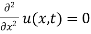
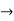 u(x,t)= 0 and u(
u(x,t)= 0 and u(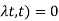
We can check by substituting that the solution fulfilling first condition is
U(x,t) = f(t-x)-f(x+t)
Additionally we want
f(t-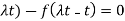
Substituting
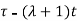
We get the condition of self-symmetry
f(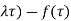
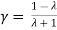
It is fulfilled by considering a simple example sin[log
With 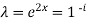
Thus in general,
f(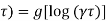
And we get the general solution as,