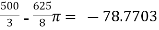Unit -3
Vector calculus
A Point function (also known as state function) is a function whose value depends on the final and initial states of the thermodynamic process, irrespective of the path followed by the process. Example of point functions are density, enthalpy, internal energy, entropy etc.
Example 1:
A reversible heat engine operates between two reservoirs at temperature of 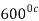 and
and 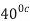 .The engine drives a reversible refrigerator which operates between reservoirs of
.The engine drives a reversible refrigerator which operates between reservoirs of 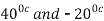 heat transfer to the engine is 2000 KJ and the network output of the combined engine is 360 kJ . Evaluate the heat transfer to the refrigerant and the net heat transfer to the reservoir at
heat transfer to the engine is 2000 KJ and the network output of the combined engine is 360 kJ . Evaluate the heat transfer to the refrigerant and the net heat transfer to the reservoir at 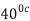
Solution:
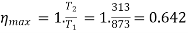
 = 0.642
= 0.642 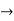
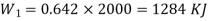
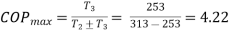
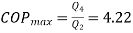
Example 2:
The e.m.f in a thermocouple with the test junction at 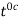 on gas thermometer scale and reference junction at ice point is given by
on gas thermometer scale and reference junction at ice point is given by
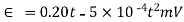
The mill voltmeter is calibrated at ice and steam points .What will this thermocouple read when the gas thermometer reads 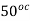 ?
?
Solution:
At ice point, when 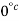 ,
,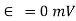
At steam point, when t= 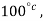
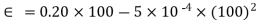
= 15 mV
At t = 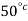 ,
,
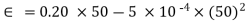
= 8.75 Mv
Thus, 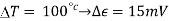
Hence, when gas thermometer reads 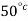 ( corresponding to 8.75 mV) ,the thermocouple will read
( corresponding to 8.75 mV) ,the thermocouple will read
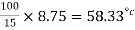
Example 3:
A frictionless piston-cylinder device contains 5kg of steam at 400 kPa and 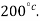 Heat is transformed to steam until the temperature reaches
Heat is transformed to steam until the temperature reaches 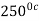 .if the piston is not attached to the shaft, and its mass is constant, determine the work done by the steam during the process. Given
.if the piston is not attached to the shaft, and its mass is constant, determine the work done by the steam during the process. Given 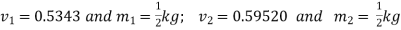
Solution:
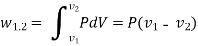
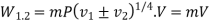
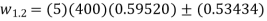
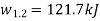
Differentiation :
Solve the following D.E
Example 1:
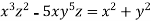
Solution: solving the equation w.r.to x,
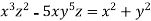
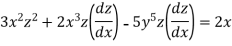
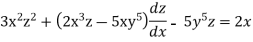
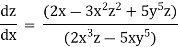
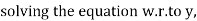
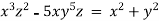
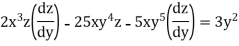
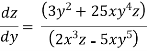
Example 2:
Find the gradient of the following:
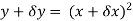
= 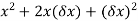
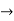
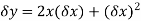
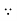 y=
y=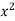
 =
= 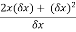 .
.
= 2x+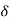
Example 3:
Consider the surface z= 10-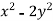 at (1,-1,7), find a 3d tangent vector that points in the direction of steepest ascent.
at (1,-1,7), find a 3d tangent vector that points in the direction of steepest ascent.
Solution:
Let our tangent vector be v= ai+bj+ck.
To find v , we have that,
The direction of steepest ascent of z(x,y) is given by the two-dimensional vector 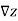 .
.
First we find the x,y components of v,then we find z component of v
Finding x,y components of v,
As the gradient provides the direction of steepest ascent, we compute it:
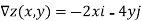
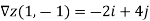
Thus, a=-2 and b=4, and are seeking a tangent vector
V=-2i+4j+ck.
Example 4:
Determine 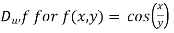 in the direction of
in the direction of 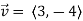
Solution:
First we calculate gradient of the points,
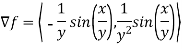
Here we require a unit vector but by our knowledge it is clear that the given vector is not so we change it into unit vector,
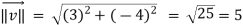
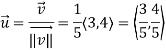
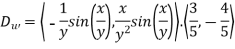
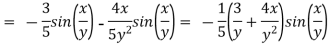
Example 1:
Compute 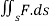 where F= (3x+
where F= (3x+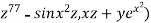 and s is the surface of the box such that 0
and s is the surface of the box such that 0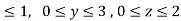 use outward normal n
use outward normal n
Solution:
Writing the given vector fields in a suitable manner for finding divergence
Div F =3+2y+x
We use the divergence theorem to convert the surface integral into a triple integral
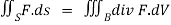
Where B is the box 0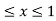 , 0
, 0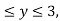
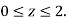
We compute the triple integral of div F=3+2y+x over the box B
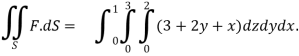
=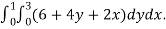
=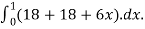
= 36+3=39
Example 2:
For F= (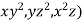 use divergence theorem to evaluate
use divergence theorem to evaluate 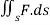 where s is the dphere of radius 3 centred at origin.
where s is the dphere of radius 3 centred at origin.
Solution:
Since div F= 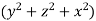 , the surface integral is equal to the triple integral.
, the surface integral is equal to the triple integral.
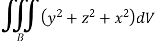
To evaluate the triple integral we can change value of variables to spherical co-ordinates,
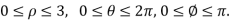
The integral is 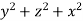 =
=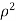 .For spherical co-ordinates, we know that the jacobian determinant is dV =
.For spherical co-ordinates, we know that the jacobian determinant is dV = 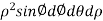 .therefore, the integral is
.therefore, the integral is
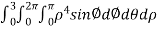 =
= 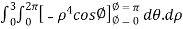
= 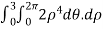
=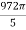
Example 1:
Find the curl of F(x,y,z) = 3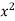 i+2zj-xk
i+2zj-xk
Curl F = 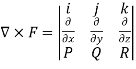
=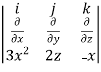
= 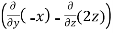 i -
i - 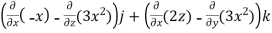
= (0-2)i-(-1-0)j+(0-0)k
= -2i+j
Example 2:
What is the curl of the vector field F= ( x +y +z ,x-y-z,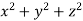 )?
)?
Solution:
Curl F = 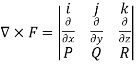
= 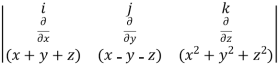
=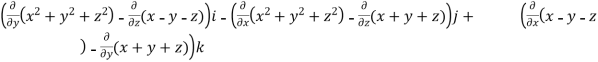
= (2y+1)i-(2x-1)j+(1-1)k
= (2y+1)i+(1-2x)j+0k
= (2y+1, 1-2x,0)
Example 3:
Find the curl of F = (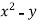 )i +4zj +
)i +4zj +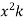
Solution:
Curl F=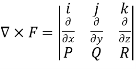
= 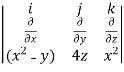
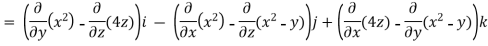
=(0-4)i-(2x-0)j+(0+1)k
=(-4)i – (2x)j+1k
=(-4,-2x,1)
Solenoidal vector formula: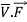 = 0
= 0
Irrotational vector formula :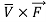 =0
=0
Example :1
Show that 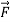 = yz
= yz +zx
+zx +xy
+xy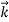
Solution:
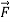 = yz
= yz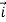 +zx
+zx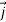 +xy
+xy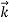
To prove : 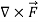 =0
=0
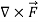 =
= 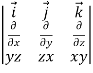
= 0
Example:2
Prove 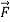 =(
=(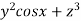 )
)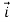 +(2ysinx-4)
+(2ysinx-4)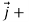 3x
3x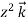 is irrotational and find its scalar potential.
is irrotational and find its scalar potential.
Solution:
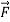 =(
=(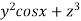 )
)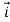 +(2ysinx-4)
+(2ysinx-4)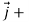 3x
3x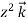
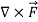 =
=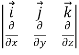
= 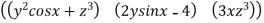
Hence,  is irrotational
is irrotational
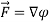
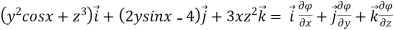
Equating the co-efficients of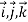 we get,
we get,
Example:1
Find the surface area for the following plane using Integration.
Solution:
z = 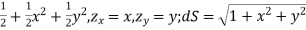 dA
dA
Using polar coordinates
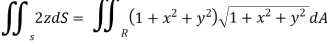
=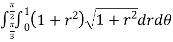
=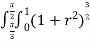 r drd
r drd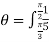
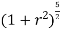
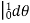 =
= 
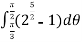
= 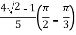
= 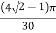
Example 2:
Find the volume enclosed by the hyperboloid 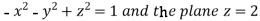
Solution:
Considering the plane z=2 and we have 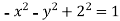 or
or 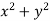 =3 and also we no that the hyperboloid interest .In the x y plane this equation is a circle of radius
=3 and also we no that the hyperboloid interest .In the x y plane this equation is a circle of radius 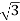 .we are trying to find the volume of a drum bounded on the bottom by z=
.we are trying to find the volume of a drum bounded on the bottom by z=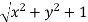 and with a top given by z=2.Therefore the volume is given in the triple integral (cylindrical coordinates).
and with a top given by z=2.Therefore the volume is given in the triple integral (cylindrical coordinates).
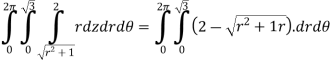
=6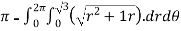
=6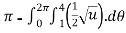 , u=
, u=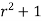
=6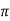 -
-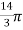
Example 1:
Compute 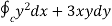
Where c is the ccw-oriented boundary of the upper-half unit disk D
Solution:
The vector integral in the above field is F(x,y) = (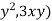 .we compute the integral using green’s theorem to convert the line integral into double integral.the integrand of the double integral is,
.we compute the integral using green’s theorem to convert the line integral into double integral.the integrand of the double integral is,
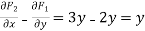
The double integration is bounded by the region D.therefore D is enclosed within the below set of values.
-1 , 0
, 0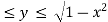
Applying green’s theorem
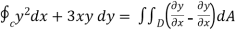
= 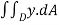
= 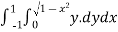
= 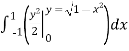
= 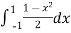
= 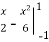 =
= 
Example 2:
For F(x,y,z)=(y,z,x) compute 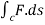
Solution:
Since we are given a line integral and need to apply a stroke’s theorem,we compute surface integral
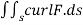
Where s is a surface with boundary c,we can choose any surface s,as long as we are oriented it so that c is a positively oriented boundary.
We need to calculate curl F using the notation
Curl F = 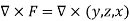
= 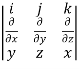
=i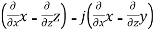 +
+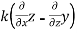
=i(-1)-j(1)+k(-1)
=(-1,-1,-1)
Next we calculate surface by,
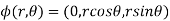 for 0
for 0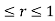 and 0
and 0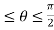
Now we calculate the normal vector n:
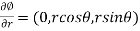
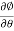
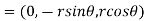
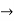
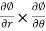 =i(r
=i(r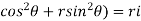
To orient the surface properly we must use the normal vector 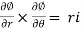
At this point we can already see that the integral 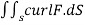 should be positive.The vector field curl F=(-1,-1,-1) and the normal vector (-r,0,0) are pointing in similar direction.
should be positive.The vector field curl F=(-1,-1,-1) and the normal vector (-r,0,0) are pointing in similar direction.
Now we compute the all pieces of the integral,
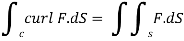
= 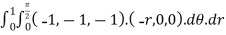
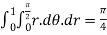
Example 3:
Use Green’s theorem to evaluate 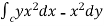 .
.
To Green’s theorem to evaluate the integral we have,
P=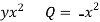
Then the Green’s theorem integral become,
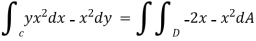
Finding the values of D in polar form
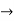
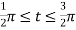 and
and 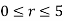
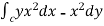 =
= 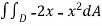
= 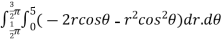
= 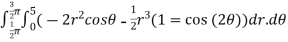
=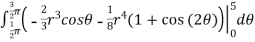
=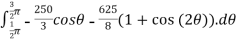
= 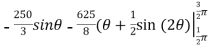
=