Module 1

DC circuits

1.1             Electrical circuits R,L,C

The three circuit elements are:

• Resistance R
• Capacitance C
• Inductance L

Resistance

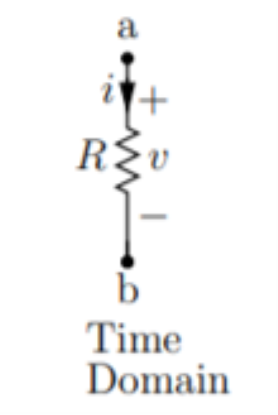
In time domain

v(t) =  R . i(t)

i(t) = v(t) /R

Resistance is the static element where v(t) versus i(t) relationship is instantaneous.

Capacitance

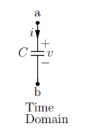
Time domain

q(t) = C v(t)

i(t) = dq/dt = C dv/dt

Dv/dt = 1/C i(t)

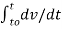= v(t) – vo(t) = 1/C 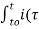) d

v(t) = v(to) + 1/C 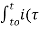) d

Unlike the resistance for capacitance v(t) versus i(t) relationship at any time t depends on the past as they involve differentials and integrals. This implies that the capacitance is dynamic element. Capacitance stores energy.

Inductance:

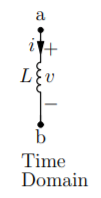
Time domain v(t) = L. Di/dt

Di/dt = 1/L v(t)

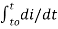  = i(t) – i(to) = 1/L 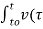) d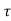

i(t) = i(to) + 1/L 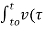) d

1.2             Voltage and current sources:

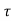
A voltage source is two-terminal device whose voltage at any instant of time is constant and is independent of the current drawn from it. Such a voltage source is called Ideal Voltage Source and has zero internal resistance.

Practically an ideal voltage source cannot be obtained.

Sources having some amount of internal resistances are known as Practical Voltage Sourcebecause of theinternal resistance the voltage drop takes place which causes the terminal voltage to reduce. The smaller the internal resistance (r) of a voltage source the closer is the Ideal Source.

The symbolic representation of the ideal and practical voltage source is shown below.

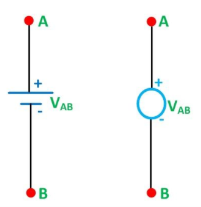
Figure A shown below shows the circuit diagram and characteristics of an ideal voltage source:

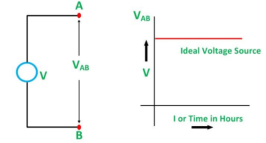
Figure A

Figure B shown below gives the circuit diagram and characteristics of Practical Voltage Source:

The example of voltage sources is batteries and alternators.

The current sources isfurther categorised as Ideal and Practical current source.

An ideal current source is a two-terminal circuit element which supplies the same current to any load resistance connected across its terminals. The current supplied by the current source is independent of the voltage of source terminals. It has infinite resistance.

A practical current source is represented as an ideal current source connected with the resistance in parallel. The symbolic representation is shown below:

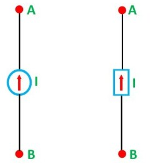
Figure C shown below shows the characteristics.

Figure D shown below shows the characteristics of Practical Current Source.

The example of current sources is photoelectric cells, collector currents of transistors.

1.3 Kirchoff’s current and voltage law
 

Kirchhoff Voltage Law:

A loop is a path around a circuit that starts and ends in the same place.

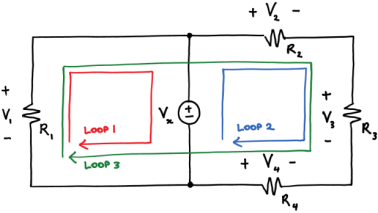
Kirchhoff's voltage law (KVL) states that around a loop:
 

Sum of voltage rises=sum of voltage drops--------------------(1)

Applying KVL around the three loops we get

V1 = Vx                                   KVL around loop 1

Vx + V4 = V2 + V3               KVL around loop2

V1 + V4 = V2 + V3             KVL around loop3  

Kirchhoff Current Law:

A node is a circuit connection that extends to all its neighbouring elements but does not contain them.

Kirchhoff’s current law states that at a node:

Sum of the in currents = sum of out currents

Applying KCL at four nodes

0 = Ix + I1 + I2        KCL at node a

I2 = I3                        KCL at node b

I3 + I4 = 0                 KCL at node c

Ix + I1 = I4                KCL at node d

Adding equations 6-9 gives the following equation:

Ix + I1 + I2 + I3 + I4 = Ix + I1 + I2 + I3 + I4.

Using KVL find the current and voltage.

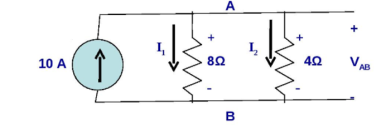
Using KVL we get

-         I1 . 8 Ω + I2 . 4 Ω =0

Solving we get

I2 = 2 I1

Using KCL we get

I1 + I2 = 10

I1 + 2I1 = 10

3I1 = 10

I1 = 3.33 A

I2 = 6.67 A

VAB = 26.33 volts

1.4             Analysis of simple circuits with dc excitation

Consider a simple circuit with DC excitation:

Analysis means to determine the voltages at all the nodes and currents in all the branches of the circuit.

A node is defined as a point where two or more components meet.

A branch is defined as any path between two nodes.

Here the nodes are 1 and 0

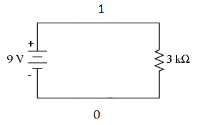
We have only two nodes here, ‘1’ and ‘0’.

‘0’  is the ground node. The ground node is at 0 volt.

Node ‘1’ is connected to the top of DC voltage source. So, it is 9 volts.

There are two branches in our circuit. One branch contains the 9V DC source and the other branch contains the 3k resistor.

From Ohm’s law we can calculate the current in the resistor.

I = V/R

This gives us a current of 9/3k = 3 mA.

The current in the resistor branch is 3 mA. And, because our circuit is one single closed loop, this current also flows in the other branch.

At this point, we know all the voltages at each node and the currents through each branch of our simple circuit.Hence, the analysis of our simple DC excitation circuit is complete.

1.5             Super position Theorem

Superposition theorem states that in any linear, active, bilateral network having more than one source, the response across any element is the sum of the responses obtained from each source considered separately and all other sources are replaced by their internal resistance. The superposition theorem is used to solve the network where two or more sources are present and connected.

If a number of voltage or current sources are acting in a linear network, the resulting current in any branch is the algebraic sum of all the currents that would be produced in it when each source acts alone while all the other independent sources are replaced by their internal resistances.

Example:

The circuit diagram is shown below consists of two voltage sources V1 and V2.

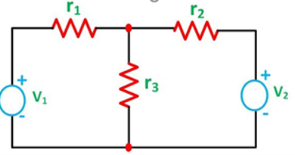
First, take the source V1 alone and short circuit the V2 source as shown in the diagram below:

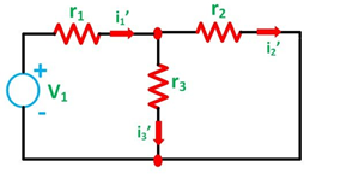
The value of current flowing in each branch, that is  i1’, i2’ and i3’ is calculated by the following equations.

i1’ = V1/ r2r3 / r2 + r3 + r1 ……………………….(1)

i2’ = i1’. r3/ r2 + r3 ………………………………(2)

The difference between the two equations gives the value of the current i3’

i3’ = i1’ – i2’
 

Next, activate the voltage source V2 and deactivating the voltage source V1 by short-circuiting it, find the various currents, that is  i1’’, i2’’, i3’’ flowing in the circuit diagram shown below:

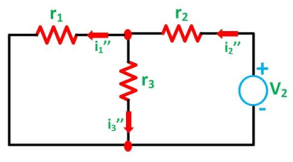
Here,

I2’’ = V2 / r1r3 / r1+r3 + r2   and i1’’ r3/ r1 + r3

And the value of the current i3’’ will be calculated by the equation shown below:

i 3 ‘’= i2’’ – i1’’
 

As per the superposition theorem, the value of current i1, i2, i3 is now calculated as:

i 3 = i3’ + i3’’

i2 = i2’ – i2 ‘’

i1 = i1’ – i1’’

The direction of the current should be taken care of while finding the current in the various branches.

The steps for solving Superposition Theorem

Considering the circuit diagramA, let us see the various steps to solve the superposition theorem:

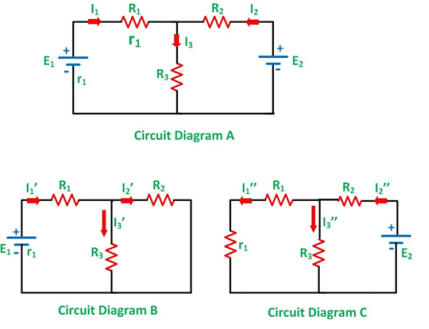
Step 1 – Take only one independent source of voltage or current and deactivate the other sources.

Step 2 – In the circuit diagram B, consider source E1 and replace the other source E2 by its internal resistance. If its internal resistance is not given, then it is taken as zero and the source is short-circuited.

Step 3 – If there is a voltage source than short circuit it and if there is a current source then just open circuit it.

Step 4 – Thus, by activating one source and deactivating the other source find the current in each branch of the network. Taking the above example find the current I1’, I2’and I3’.

Step 5 – Now consider the other source E2 and replace the source E1 by its internal resistance r1 as shown in the circuit diagram C.

Step 6 – Determine the current in various sections, I1’’, I2’’ and I3’’.

Step 7 – Now to determine the net branch current utilizing the superposition theorem, add the currents obtained from each individual source for each branch.

Step 8 – If the current obtained by each branch is in the same direction then add them and if it is in the opposite direction, subtract them to obtain the net current in each branch.

The actual flow of current in the circuit C will be given by the equations shown below:

I1 = I1’ – I1’’

I2 = I2’ – I2 ‘’

I3 = I3’ – I3 ‘’

Problem:

Using Superposition theorem determine the voltage drop and current across the resistor 3.3K as shown in figure below

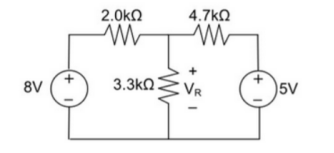
Step 1:

Remove 8V power supply from the original circuit such that the new circuit becomes as the following and measure the voltage across resistor.

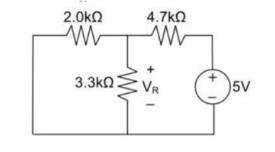
Here 3.3 K and 2K are in parallel therefore the resultant resistance will be 1.245K

Using voltage divider rule across 1.245K will be

V1 =[1.245/(1.245+4.7)] * 5 = 1.047V

Step 2:

Remove the 5V power supply from the original circuit such that the new circuit becomes the following and then measure the voltage across resistor.

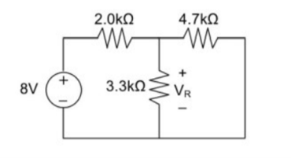
Here 3.3K and 4.7K are in parallel therefore the resultant resistance will be 1.938K. Using voltage divider rule voltage across 1.938K will be

V2 =[1.938(1.938+2)] *8 = 3.9377V

Therefore, voltage drop across 3.3K resistor is V1+V2 = 1.047 + 3.9377 = 4.9847V

1.6  Thevenin theorem

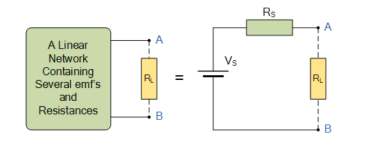
Thevenin’s Theorem states that “Any linear circuit containing several voltages and resistances can be replaced by just one single voltage in series with a single resistance connected across the load”.

To simplify any electrical circuit, to an equivalent two-terminal circuit with just a single constant voltage source in series with a resistance (or impedance) connected to a load as shown below.

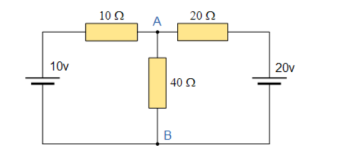
Consider the circuit as shown in figure:

In order to analyse the circuit initially remove the 40Ω load resistor connected across the terminals AB and remove any internal resistance associated with the voltage source.

This is done by shorting out all the voltage sources connected to the circuit. Therefore v=0 or open circuit any connected current sources making i=0.

This because we want to make an ideal voltage source or ideal current source making for circuit analysis.

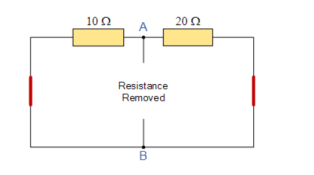
The value of the equivalent resistance, Rs is found by calculating the total resistance looking back from the terminals A and B with all the voltage sources shorted. 

10 Ω resistor in parallel with 20Ω resistor

RT  = R1 x R2/ R1 + R2 = 20 x 10 / 20 + 10 = 6.67 Ω

Find the equivalent voltage

To reconnect the two voltages back into the circuit Vs=VAB the current flowing around the loop is calculated as:

I = V/R = 20 V – 10V / 20 Ω + 10 Ω = 0.33 Amps.

The current is common to both resistors so the voltage drop across the 20Ω resistor or the 10Ω resistor is calculated as:

VAB  = 20 –( 20 Ω x 0.33 amps) = 13.33 volts

VAB = 10 + (10 Ω x 0.33 amps) = 13.33 volts

The Thevenin’s Equivalent circuit is a series resistance of 6.67Ω and the voltage source of 13.33 V.

If 40Ω resistor is connected back to the circuit, we get

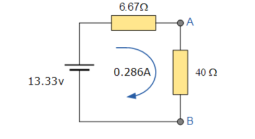
And from this the current flowing around the circuit is given as:

I = V/R = 13.33/6.67 + 40 = 0.286 amps.

Problem:

For the circuit as shown in figure find the current through RL = R2 = 1Ω resistor (Ia-b) branch using Thevenin’s theorem. Find the voltage across the current source.

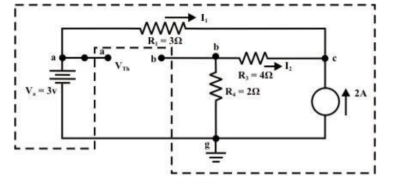
Step 1: Disconnect the load resistance and reconnect the circuit.

Step 2: Apply any method to calculate Vth

At node C

2 + I1 + I2 =0

2 + (3 -Vc)/3 + (0-Vc/6) --Vc = 6V

The currents I1 and I2 are computed by the following expressions:

I1 = Va -Vc/3 = 3-6/3 = -1A (I1 is flowing from c to a)

I2 = 0 – Vc/6  = -6/6 = -1A (I2 is flowing from c to a)

Step-3:

Redraw the circuit indicating the direction of currents in different branches. One can find the Thevenin’s voltage VTh using KVL around the closed path ‘gabg’

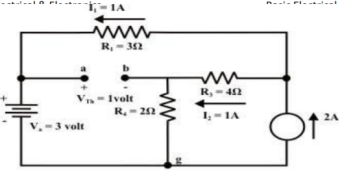
VTh = Vag−Vbg = 3 − 2 =1volt

Step 4:

Replace all sources by their internal resistances. In this problem, voltage source has an internal resistance zero (0) (ideal voltage source) and it is short-circuited with a wire.

On the other hand, the current source has an infinite internal resistance (ideal current source) and it is open-circuited (just remove the current source).

Thevenin’s resistance RTh of the fixed part of the circuit can be computed by looking at the load terminals ‘a’- ‘b’

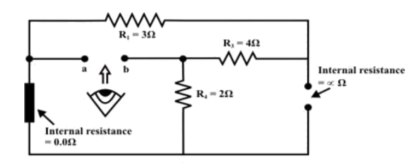
RTh = ( R1 + R3 ) & R4 = ( 3 + 4 )&2 = 1.555Ω

Step-5: Place RTh in series with VTh to form the Thevenin’s equivalent circuit. Reconnect the original load resistance RL = R2 = 1 Ω to the Thevenin’s equivalent circuit .

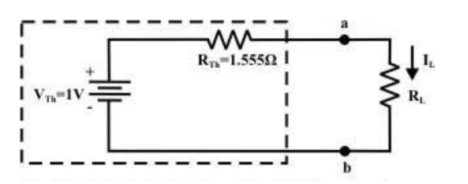
Step-6: The circuit is redrawn to indicate different branch currents. Referring to one can calculate the voltage Vbg and voltage across the current source (Vcg ) using the following equations.

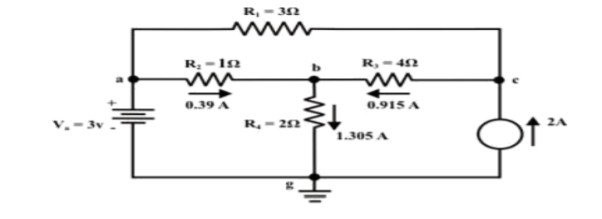
Vbg = Vag−Vab = 3 − 1 × 0.39 =2.61 volt.

Ibg = 2.61 2 = 1.305 A;

Icb = 1.305 − 0.39 = 0.915 A

Vcg = 4 × 0.915 + 2 ×1.305 =6.27 volt.

For the circuit shown in figure, find the current IL through 6 Ω resistor using Thevenin’s theorem.

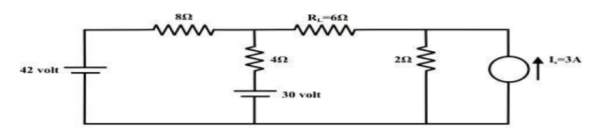
Step-1:

Disconnect 6 Ω from the terminals ‘a’ and ‘b’ and the corresponding circuit diagram. Consider point ‘g’ as ground potential and other voltages are measured with respect to this point.

Step-2:

Apply any suitable method to find the Thevenin’s voltage (VTh )

KVL is applied around the closed path ‘gcag’ to compute Thevenin’s voltage.

42 – 8I – 4I -30 = 0 ; I = 1A

Vag = 30+4 = 34 volt

Vbg = 2 x 3 = 6 volt

Vth = Vab = Vag – Vbg = 34 -6 = 28 volt

Step-3:

Thevenin’s resistance RTh can be found by replacing all sources by their internal resistances all voltage sources are short-circuited and current sources are just removed or open circuited.

Rth = (8 x4) / 12 + 2 = 14/3 = 4.666Ω

Step-4:

Thevenin’s equivalent circuit is now equivalently represents the original circuit

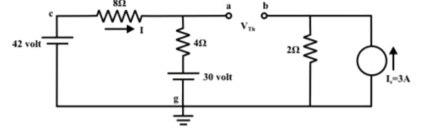
IL = Vth / Rth + RL = 28 / 4.666 +6 = 2.625 A

Norton’s Theorem

Norton’s Theorem states that “Any linear circuit containing several energy sources and resistances can be replaced by a single Constant Current generator in parallel with a Single Resistor”.

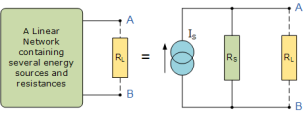
To find the Norton’s equivalent remove the centre 40Ω load resistor and short out the terminals A and B to give us the following circuit.

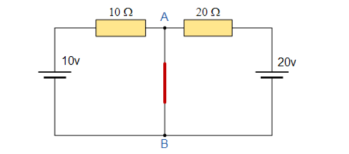
When the terminals A and B are shorted together the two resistors are connected in parallel across their two respective voltage sources and the currents flowing through each resistor as well as the total short circuit current can now be calculated as:

With A-B shorted out

I1 = 10 / 10 = 1A        I2 = 20/20 = 1A , Therefore I short-circuit = I1 + I2 = 2 amps

If we short-out the two voltage sources and open circuit terminals A and B, the two resistors are connected in parallel. The value of the internal resistor Rs is found by calculating the total resistance at the terminals A and B giving us the following circuit.

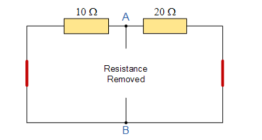
The equivalent resistance is given by 10Ω resistor in parallel with 20 Ω resistor

RT = R1 x R2 / R1 + R2 = 20 x 10 / 20 + 10 = 6.67 Ω.

Norton’s equivalent circuit.

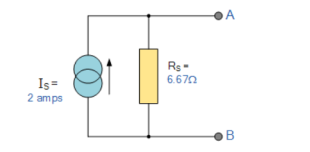
To solve with the original 40Ω load resistor connected across terminals A and B as shown below.

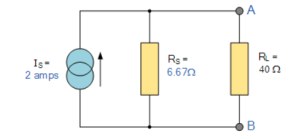
The two resistors are connected in parallel across the terminals A and B which gives us a total resistance of:

RT = R1 x R2 / R1 + R2 = 6.67 x 40 / 6.67 + 40 = 5.72 Ω.

The voltage across the terminals A and B with the load resistor connected is given as:

Va-b = I x R = 2 x 5.72 = 11.44V

Then the current  flowing in the 40 Ω load resistor can be found as :

I = V / R = 11.44 / 40 = 0.286 amps.

Problem:

Find RN, IN, the current flowing through and load Voltage across the load resistor in fig (1) by using Norton’s Theorem.

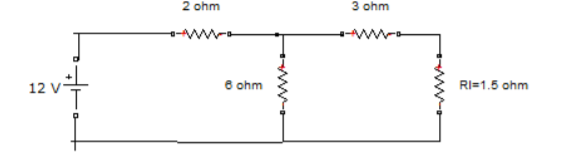
Step 1:

Short the 1.5 Ω load resistor.

Step 2:

Norton current.

Short AB terminals to obtain IN .The total resistance of the circuit is

2Ω + (6Ω || 3Ω)

RT = 4 Ω

IT = V / RT = 12/ 4 = 3 A

IN = 3 A x [ 6Ω / 3 + 6 )] = 2A

IN = 2A

Step 3:

Open current sources, Short Voltage sources and Open Load resistor.

Step 4:

Calculate Norton Resistance (RN)

Reduce 12V dc source. 3Ω resistor is in series with combination of 6Ω and 2Ω resistor

3Ω + (6Ω||2Ω)

3Ω + 1.5 Ω = 4.5 Ω; RN = 4.5 Ω

Step 5:

Connect RN in parallel with current source IN and the load resistor.

Step 6:

The load current through Load resistor

IL = IN x [ RN/(RN + RL)

=2 A x ( 4.5 / 4.5 + 1.5 K) = 1.5 A

IL = 1.5 A

The voltage across load resistor

VL = IL x RL

= 1.5 x 1.5

VL = 2.25 V

1.7             Time domain analysis of first order RL and RC circuits

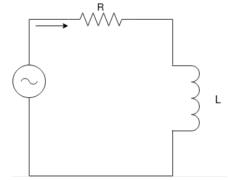
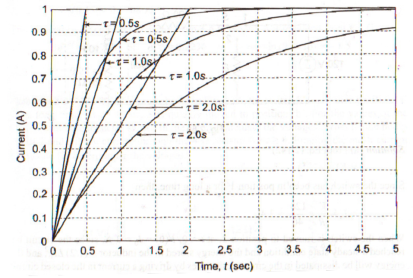
When switch ‘S’ is close at t>0 the as per KVL network equation will be …

R i(t) + L di(t)/dt = Vs ------------------------------------(1)

Above equation is non homogeneous equation linear differential equation of first oder. The solution of equation 1 will give i(t) which consists of two components :

Complimentary function

Which will satisfy di(t)/dt + R/L i(t) =0

Particular integral (if(t)) which will satisfy

R i(t)  + L di(t)/dt = Vs

Thus the complete solution wil be

i(t) = in(t) + iJ(t)---------------------------------------(2)

i(t) = Io e –(R/L)t = Io e –(t/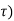-------------------------------------(3)

Where 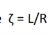   time constant of RL circuit.

Equation (3) provides the natural response where

in(t)  = K e –(R/L) t = K e –(t/τ) ----------------------------------(4)

Eq (1) can be written with i(t) = I constnt

RI + L dI/dt = Vs -------------------------------------------(5)

Since I= constsnt

L dI/dt =0

If(t) = I = Vs/R --------------------------------------------(6)

Substitute eq.4 and eq.6 yeilds the solution of eq(1)

i(t) = K e -t/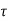 + Vs/R = K e-t/τ-------------------------------------------(7)

K is determined from initial condition that is t=0 and eq(7) will be

K = -Vs/R = -I ----------------------------------------------------(8)

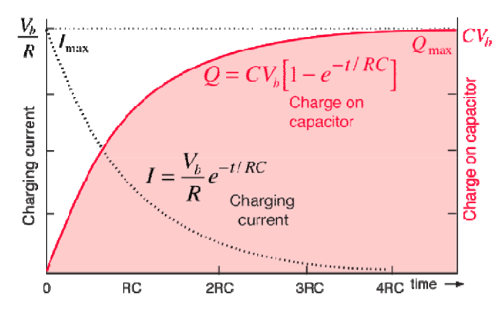
i(t) = Vs/R (1 – e –(R/L) t)

i(t) = I(1 – e -t/τ)                                                  for t>0

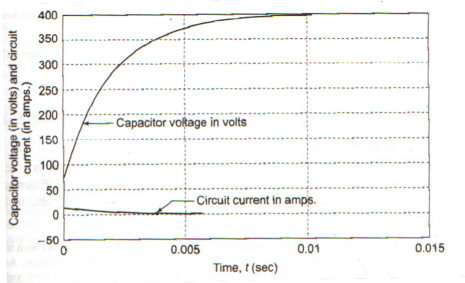
Series RC circuit:

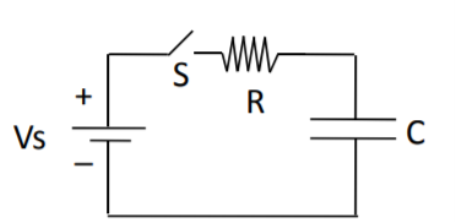
Fig. Shows a series RC circuit connected across a DC source through a switch S.

It is assumed that capacitor voltage id V0 When switch ‘S’ is close at t>0 the as per KVL network

Equation will be …

Vs – R i(t) – vc(t) =0 ------------------------------------------------(9)

For analysis of circuit of the figure the capacitor voltage Vc(t) is chosen as variable .

Substituting i(t) = c dvc(t)/dt in eq(9) we get

Eq(10) is like eq(1) it is also non homogeneous equation linear differential equation

Of first order .

Therefore the solution is similar to eq(1)

Vc(t) = k e -t/τ + Vs ---------------------------------------------(11)

In eq.(11) the time constant is τ = RC

By substituting value of K in eq(11) and after simplification we get --------

Vc(t) = Vo e (-t/τ) + Vs ( 1 – e -t/τ) V      for t>0------------------------------------------(12)

The expression for the current in the circuit is given by ---------

i(t) = C dvc(t)/ dt

i(t) = C [ (-1/τ Vo e -t/τ  ) + ((-1/τ Vs e -1/τ  )]

i(t) = C/RC (Vs – Vo) e -t/τ

References: