Module- 1
Atomic and molecular structure
Is a very fundamental equation used in quantum physics it is also referred as just Schrodinger equation, it’s basically a differential equation used to solve problems, that are based on structure of atoms. The equation is used widely in Physics and Chemistry.
Schrodinger wave equation describes the change of a physical quantity with time or the behaviour of a particle in a field of force. Erwin Schrödinger was the one developed the equation was even awarded the Nobel Prize in 1933. Schrodinger wave equation is a mathematical expression that describes the energy and position of the electron present in space and time, taking into account the matter wave nature of the electron inside an atom
Schrodinger equation gives us a detailed account of the wave probability that hold the movement of some particles, the equation gives a detail of the form of wave functions. The equation also details, how these waves are however influenced by external factors. Moreover, the equation makes use of the energy conservation concept that offers details about the behaviour of an electron that is attached to the nucleus.
Besides, by calculating the Schrödinger equation we obtain Ψ and Ψ2 which helps us determine the quantum numbers as well as the orientations and the shape of orbitals where electrons are found in a molecule or an atom.
There are two equations which are time-dependent Schrödinger equation and a time-independent Schrödinger equation
The Time-dependent Schrödinger equation is represented as;
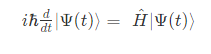
The Time-dependent Schrödinger equation in position basis is given as
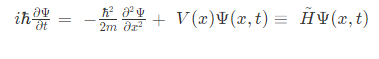
Where,
i = imaginary unit, Ψ = time-dependent wavefunction, h2 is h-bar, V(x) = potential and
H^ = Hamiltonian operator
Particle in a Box and their Applications
In Quantum Physics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly utilized as a hypothetical example to describe the differences between quantum and classical systems. For example, in classical systems, a particle trapped inside a large box moves more freelyand cannot be spotted in a single position and can move at any speed within the box. However, when the space becomes very narrow (on the scale of a few nanometres), quantum effects become veryimportant. The particle may only occupy certain positive energy levels. Likewise, the particle can never have zero energy, meaning that the particle can never "sit still" or be stationary. Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes.
The particle in a box model found in quantum mechanics is one of the very few problems which can be solved analytically, without approximations. As the particle shows its simplicity, and without the need of mathematics, the model allows insight into quantum effects without the need for complications. It serves as a simple illustration of how energy quantization’s(energy levels), which are found in more complicated quantum systems such as atoms and molecules, are present.
The Schrödinger equation differentiates particles based on their potential they lie in. For a free particle, previously discussed, we assumed the most basic potential: no potential, V(x)=0. This describes a free particle, but assumes that the particle will never experience a potential at any x-position it occupies. This is unrealistic, and hence we need to start moulding our potential to account for this experimental result. In atomic systems, there are places where an electron will NEVER be (or more accurately, it is extremely unlikely). In order to constrain the electron from ever occupying these locations we will set the potential at these locations to be infinity (the potential barrier to occupy that location cannot be overcome).
For real applications of this type of problem, we can look at conjugated polymers (series of double bonds or aromatic groups). For these systems, electrons can move (almost) freely inside the band gap (fermi level); however, they cannot escape the molecule (it is not a conductor). The most famous example of these conjugated system (modelled almost exactly by this type of approximation) is the quantum dot: small semiconductors whose colour can be changed based on the size of the dot.
We call this type of problem the "infinite square well" or "particle in a box" and it can be pictorially modelled as:

Fig 1: As one can visually see, the potential is now a piecewise function. We can therefore break up the Schrödinger equation into a part where the potential is infinity and a part where the potential is zero.
The hydrogen atom is present in its simplest atomic form in nature and, therefore, a show a good starting point to study structures with respect to atoms and atomic structure. When the hydrogen atomstructure is closely observed the atoms mainly consists of a single negatively charged electron that revolves about a positively charged proton. In Bohr’s model, when examined we observe the proton in a circular orbit due to the electron, the circular orbit is perfectly due to an attractive Coulomb force. The proton is approximately 1800 times larger than the electron, so the protonshows very less movement in response to the force exerted on the proton by the electron. (This is analogous to the Earth-Sun system, where the Sun moves very little in response to the force exerted on it by Earth.).
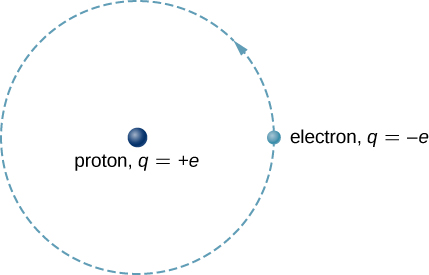
Fig 2: A representation of the Bohr model of the hydrogen atom.
With the assumption of a fixed proton, we focus on the motion of the electron.
s orbitals; these have the most radial nodes (where the wave function for a given r goes to zero) out of the orbital shapes of the same n, so there is less spacefor the electrons, which expands the orbital radius to allow electrons to reach in farther.
This can be seen in the radial density distributions:
These graphs plot the time-averaged position of electron density as one increases the viewing window, we have of a given hydrogen atomic orbital.
On observation the s orbitals reach in the farthest, and it can be determined from the "farthest penetration extent" as pointed out.
The f orbital of the same n is the least penetrating, as it tapers off at around 8 bohr radii, whereas the s orbital of the same n tapers off at less than 1 bohr radius from the nucleus (r=0)
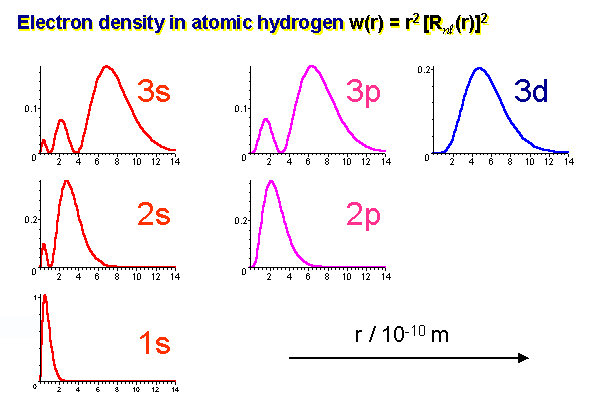
Fig 3: Electron density representations in various orbitals.
Molecular Orbital Theory was initially used to explain the bonding in molecules that could not be explained by Valence Bond Theory. These are the molecules that generally involve some attribute resonance. Resonance implies that a bond is neither single nor double but some hybrid of the two. Valence bond theory only describes the bonding of single or double or triple bonds. It does not provide an explanation for resonance bonding.
Molecular orbital theory does describe resonance.
- The Rules of Molecular Orbital Theory:
First principle: The number of molecular orbitals produced will be always equal to number of atomic orbitals brought by the atoms that have combined.
Second principle: Bonding molecular orbitals are lower in energy that the parent orbitals, and the antibonding orbitals are higher in energy.
Third principle: Electrons of the molecule are placed at orbitals from lowest to successively higher energy
Fourth principle: Atomic orbitals join together to form molecular orbitals most effectively when the atomic orbitals are of the same energy.
Principle 1: Example - Hydrogen (H2) Each hydrogen atom has a single valence bond orbital, this being the 1s orbital. Two molecular orbitals
can be formed by the constructing and destructing overlap of these two atomic orbitals. if we have two 1s atomic orbitals only two molecular orbitals are formed from them. This is the First Principle.
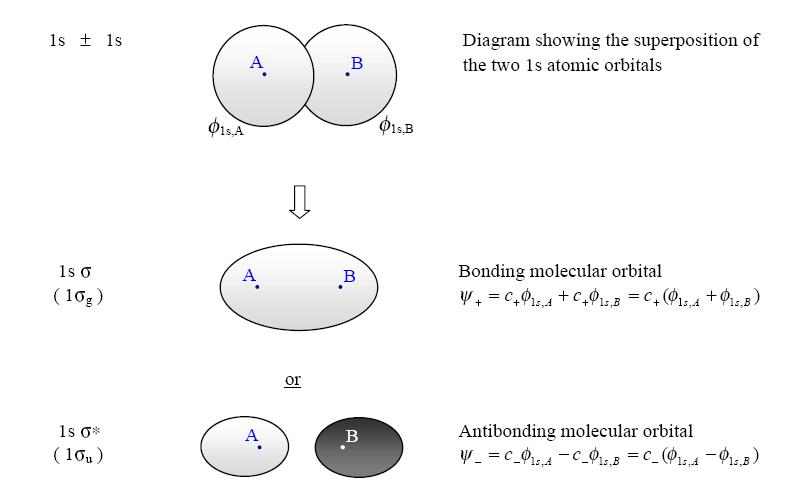
Fig4: According to MO Theory, the two molecular orbitals that are formed are called s (sigma = bonding) and s* (sigma star = antibonding). In the case of H2 both of the valence electrons that form the bond between the hydrogens fill the bonding or s orbital.
Principle 2 & 3: This interaction of atomic orbitals, which gives rise to the molecular orbitals, can also be shown in the form of an orbital (electron) energy diagram which shows the relative energies of the orbitals. In the given specific case of hydrogen each of the isolated atoms has one electron in its 1s orbital and when the atoms combine to form H2 the two electrons may be joined (with opposite spins) in the bonding molecular orbital, as shown below. The second principle explains why electrons will want to occupy molecular orbitals in the first place. As stability comes from lowering energy needs. Anyway...because the bonding molecular orbitals provide a lower energy, a more stable state is found for the electrons, they fill these orbitals first. This could explain the third principle statement also.
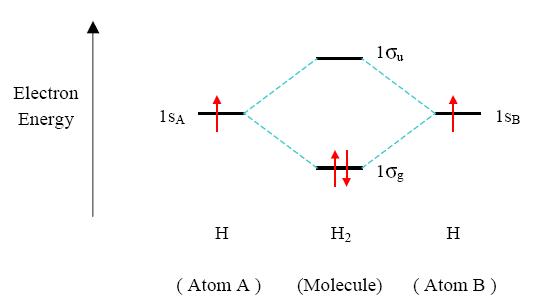
Principle 4: In H2 two 1s orbitals were combined were to form a single lower energy s molecular orbital. The fourth principle states that stability of molecular orbitals is easier to form when built out of atomic orbitals of same energies. This means that 1s orbitals should join with 1s orbitals and 2p orbitals should combine with 2p orbitals etc. to form the most stable molecular orbitals.
Fig 8: Filling up the Molecular Orbitals:
We Start with:

We then form Molecular Orbitals:
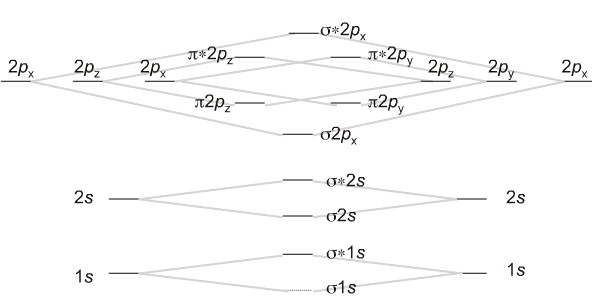
Which fill from lowest to highest energy as follows:
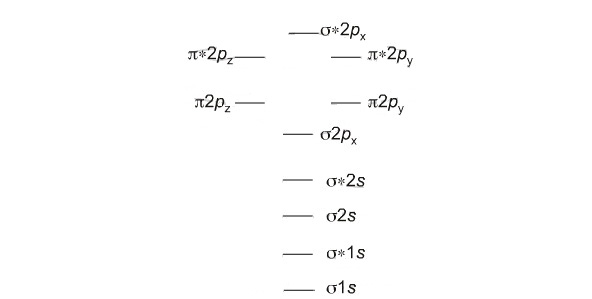
Formation of Homo and Hetero Diatomic molecules and plots of energy level diagram
There are hundreds of diatomic molecules. This list includes diatomic elements and diatomic chemical compounds.
Mononuclear Diatomic Molecules
Some of these molecules consist of one element or are diatomic elements. Diatomic elements are examples of homonuclear molecules, where all of the atoms in the molecule are the same. The chemical bonds between the atoms are covalent and nonpolar. The seven diatomic elements are:
Hydrogen (H2)
Nitrogen (N2)
Oxygen (O2)
Fluorine (F2)
Chlorine (Cl2)
Iodine (I2)
Bromine (Br2)
5 or 7 Diatomic Elements
Some sources show that there are five diatomic elements, rather than seven. This is because only five elements can form stable diatomic molecules at standard temperature and pressure: the gases hydrogen, nitrogen, oxygen, fluorine, and chlorine. Bromine and iodine form homonuclear diatomic molecules at slightly higher temperatures. It's possible that an eighth element forms a diatomic molecule.
Heteronuclear Diatomic Molecules
Many diatomic molecules consist of two elements. In general, most elements form diatomic molecules, particularly when temperatures are high. However, when a certain temperature is past, all molecules break into their constituent atoms. However, the noble gases do not form diatomic molecules. Diatomic molecules consisting of two different elements are called heteronuclear molecules. Here are some heteronuclear diatomic molecules:
CO
NO
MgO
HCl
KBr
HF
SiO
- Plots of energy level diagram of molecular orbitals
The first ten molecular orbitals may be arranged in order of energy as follows
σ(1s) <σ∗(1s) <σ(2s) <σ∗(2s) < π(2px) = π(2py) <σ(2pz) < π∗(2px) =π∗(2py) <π∗(2pz)

- In 1,3-Butadiene consists of two double bonds which are conjugated.
- The structure of the molecule is formed from 4 sp2 hybridised C atoms, each contributing a p atomic orbital that consists of 1 electron.
- An alternative way is to combine the ᴨ molecular orbitals of two ethene molecules, which thereby helps to consider "building" the π molecular orbitals.
- This requires phases that are in and out considering an in-phase and an out-of-phase combination thefor both the π and π* of ethene.
- When taken in both ways, it finally results in the same set that consists same set of 4 π molecular orbitals.
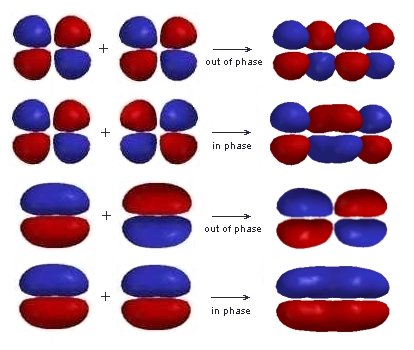
- As we go up the diagram the number of nodes and the number of anti-bonding interactions increases.
The diagram The diagram to the right shows the relative energies of π molecular rthe π molecul orbitals of 1,3-butadiene (derived from ethene) and the electron cconfiguration. Configuration. The horizontal The horizontal center line denotes the energy of a C atomic p orbital. Orbital orbital. Orbitals below that line are bonding those above are anti- Bonding. We now have we now have4 electrons to arrange, 1 from each of the original atomic p orbi Atomic p orbitals. These are all paired in the two stabilised pi bonding orbitorbitals, bonding π1 and π2. The highest occupied molecular orbital or HOor LOMO is π2 in 1,3-butadiene (or any simple conjugated diene Diene). In contrast, the In contrast the anti-bonding π* orbitals contain no electrons. The lowest unoccu lowest unoccupied orbital or LUMO is π3 in 1,3-butadiene (or any simple conjug single conjugated diene).
| 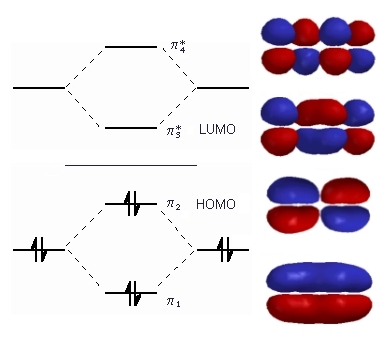 |
By counting the number of bonding and anti-bonding interaction in each the relative energies of these orbitals can be calculated:
- π1 has bonding interactions between C1-C2, C2-C3 and C3-C4
- Overall = 3 bonding interactions
- π2 has bonding interactions between C1-C2 and C3-C4 but anti-bonding between C2-C3
- Overall = 1 bonding interaction
- π3 has bonding interactions between C2-C3 but anti-bonding between C1-C2 and C3-C4
- Overall = 1 anti-bonding interaction
- π4 has anti-bonding interactions between C1-C2, C2-C3 and C3-C4
- Overall = 3 anti-bonding interactions
Pi Molecular orbital of Benzene and aromacity
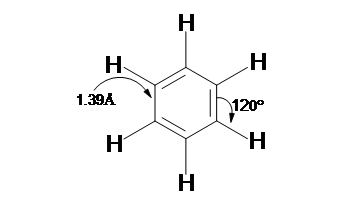
- Benzene (C6H6) structure consists of a ring of six carbon atoms each of these carbon atoms is attached with a hydrogen atom and is a planar molecule.
- A perfect regular hexagon shape is obtained with the six carbonatoms. All of the carbon-carbon bonds present in the Benzenethe exact similarlengths somewhere between single and double bonds.
- The Benzene molecule is partially unstable due to thepresence of delocalized electrons above and below the plane of the ring.
- Benzene is known to resist reactions that involve addition reactions as these reactions would breakthe delocalization and the stability is lost.
The resulting molecule of Benzene is planar in shape because of the aromaticity of benzene, the resulting molecule of benzene consists of each C-C bond being 1.39 Å in length and each bond angle being 120°. This brings us to consider how it's possible to have all of the bonds to be the same length if the ring is conjugated with both single (1.47 Å) and double (1.34 Å), a very important aspect here to be noted is that thereis absence of distinct single or double bonds presentwithin the benzene. Rather, when the ring is delocalized then the ring makes each count as one and a half bonds between the carbons this can however be proved experimentally as the actual bond length lies somewhere in between a single and double bond. Finally, there are a total of six p-orbital electrons that form stable electron clouds above and below the aromatic ring.
If the temperature is increased for a reaction or a catalyst is added to the reaction and if benzeneis forced to react under these conditions, then benzene undergoes substitution reactions rather than the addition reactions that are typical seen in alkenes. These reactions prove that benzene core that has a six carbon is stable to chemical modifications. The mutual contrast that is shown by a high degree of unsaturation (low H:C ratio) and high chemical stability for benzene and related compounds remained an unsolved mystery. Eventually, the planar ring of carbons and the regular hexagon structure was adapted, and the chemical stability and exceptional thermodynamic systems was attributed to resonance stabilization of a conjugated cyclic triene
The Crystal field theory (CFT) is a model for the bonding interaction between transition metals and ligands. It describes the effect of attraction between the positive charge of the metal cation and negative charge on the non-bonding electrons of a ligand. When the ligand approaches the central metal ion the dangerously of electronic orbital states, usually d or f orbitals, are broken due to the statistic electric field by a surrounding charge distribution. CFT successfully accounts for some magnetic properties, colours, hydration energies of transition metal complexes, but it does not help to describe bonding
2 Energy level diagrams for transition metal ions and their magnetic properties
Fig.6 Energy level diagram for transition metal ions
3 Magnetic properties of transition metal ions
There are various substances which show magnetic behaviour. There are few substances that are attracted by the magnetic field and are called paramagnetic. This phenomenon is called Para magnetism. Paramagnetic property is only seen when the substance has one or more unpaired electrons. When a substance possesses a permanent magnetic moment, it is known as ferromagnetic and the phenomenon is called ferromagnetism. On analysis, we also have substances which are repelled by magnetic field and are called as diamagnetic substances. A substance shows diamagnetism when it has only paired electrons.
Most of the transition elements show paramagnetic behaviour. The unpaired electrons in (n-1) d orbitals are responsible for the magnetic properties. The paramagnetic character of the transition metals increases on moving from left to right as the number of unpaired electrons increases from one to five. The middle elements are found to possess the maximum paramagnetic property. The magnetic properties decrease with the decrease in the number of unpaired electrons. The transition metals which contain paired electrons depict diamagnetic behaviour.
Most solid substances are known to be insulators, and in terms of the band theory of solids this implies that there is a hugeforbidden gap between the energies of the conduction band and the valence electrons.
In gaseous substances, the arrangement of molecules is spread far as the molecules are in random motion and far apart and are not so close to each other. In liquids, the molecules are closer to each other when compared to the gaseous substances. But, in solids, the molecules are closely arranged together, due to this the atoms of molecules tend to move into the orbitals of neighbouring atoms. Hence, when atoms come together the electron orbitals overlap.
In solids, due to the intermixing of the atoms several bands of energy levels are formed. This set of energy levels are called as energy bands.
Formation of Energy Bands
In an isolated atom, a definite energy is possessed by the electrons in each orbit. However, in the case of solids, the energy level of the outermost orbit electrons is affected by the neighbouring atoms.
When two isolated charges are brought close to each other, the nearest atomic nucleus provides the attractive force for the electrons present in the outermost orbit. Due to this, the values of energy levels of electrons will be at a value higher than or lower than the original level of the electron resulting in the energies of the electrons will not be at the same level,
Energy bands are the different energy levels present in groups which are exhibited by the electrons in the same orbit that show different energy levels.
However, the presence of the neighbouring atoms does not have any effect on the electrons that are present in the inner orbit.
Classification of Energy Bands
Valence Band
The electrons present in the outermost shell are called as valence electrons. These valence electrons display different levels of energy, resulting in an energy band known as valence band. The valence band are known to have the highest occupied energy.
Conduction Band
The valence electrons are known to sometimes leave the outermost orbit as they are not held tightly to the nucleus, these electrons can even move out of the orbit at even room temperature and become free electrons. These free electrons are known to show conduction of current in conductors and are also called conduction electrons. The energy levels are the lowest, in the conduction bans that contains conduction electrons.
Forbidden Energy Gap
The gap that exists between between the valence band and the conduction band is referred to as forbidden gap. According to its name,the forbidden gap doesnot show the presence of any electrons and doesn’t have any energy. If the forbidden energy gap shows a greater gap, then the valence band electrons are tightly bound or firmly attached to the nucleus.
The figure below shows variations of the conduction band, valence band and the forbidden energy gap.
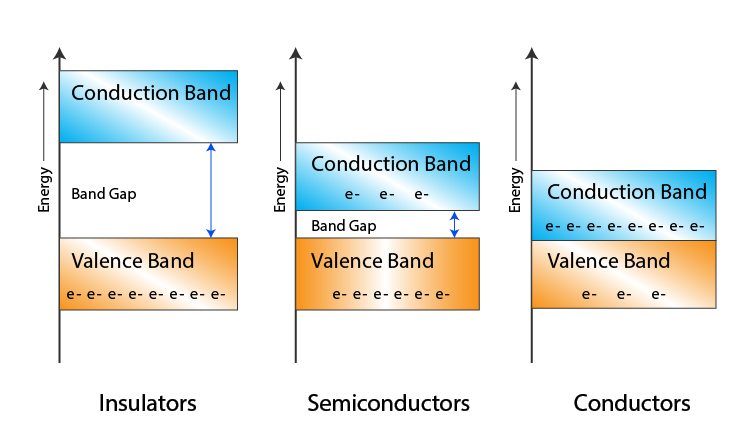
Fig 7: Based on the size of the forbidden gap the, Insulators, semiconductors and conductors are formed
Conductors
Based on the size of the forbidden gap conductors are formed for example, Gold, Aluminium, Silver, Copper, these conductors allow an electric current to flow through them.
In some cases, there is absence of forbidden gap between the conduction band and valenceband in such cases overlapping of both the bands occurs and the number of free electrons will increase for a given room temperature.
Insulators
Good examples of Insulators are Glass and wood and they do not allow electricity to pass through them. Another feature in them include that they possess high resistivity and show very low conductivity.
In case of the Insulators there is no movement of Electrons from the valence band to the conduction band and cannot conduct current therefore, the energy gap in the insulator is very high up to 7eV.
Semiconductors
The best examples of semiconductors are,Germanium and Silicon. The electrical properties of these two substances lies between the semiconductors and the insulators. As seen above in the diagram the valence band is full and the conduction band is empty, but the forbidden gap between these two bands is minute which is about 1eV, thus semiconductors need very less conductivity. For Germanium, the forbidden gap is 0.72eV and for Silicon, it is 1.1eV.
During the production of semiconductors, an important step called Doping is carried out, it involves the intentional addition of impurities into an intrinsic semiconductor in order to modify its structural, optical and electrical properties. The material that is subjected to doping is called extrinsic semiconductor. A semiconductor that is subjected to such high treatment acts like a conductor rather than a semiconductor in such cases it is referred to as degenerate semiconductor.
Energy states are allowed within the band gap during doping of semiconductors, but this depends on the dopant type that corresponds to the energy level. In other words, near the conduction band the electron donors’impurities create states and the electron acceptors impurities likewise create states near the valence band. The gap that exists between these energy states and the energy band is called as dopant-site energy.
Dopants also have the important effect of shifting the energy bands relative to the Fermi level, the Fermi level must remain constant in the Thermodynamic Equilibrium, the energy band that with respect to the dopant that has the greatest concentration will be seen closest to the Fermi level. Stacking layers of materials with different properties leads to many useful electrical properties induced by band bending if the interfaces can be made cleanly enough.
Reference:
- An Introduction to atomic and molecular structure, Harry B Gray
- Elements of organic chemistry, Issak Zimmerman & Henry Zimmerman
- Atoms and molecules, Mitchel Weiss luth