Module 3
Intermolecular Forces and Potential Energy Surfaces
The properties like melting point and boiling point can be a measure to show how strong the attractive forces exist between molecules are individual molecules. We can also call these as intermolecular forces. The general principle being as bons become more polarized, the charges on the atoms become greater, subsequently the intermolecular attraction increases, which leads to higher boiling point.
The three intermolecular forces are as follows
- Ionic bonds
- Hydrogen bonding called
- Van der Waals dipole-dipole interaction.
- Ionic forces:
Are the interactions between charged molecules or atoms (ions).
Positively charged ions, are Na (+), Li (+), and Ca (+), they are called as Cations, on the other hand the negatively charged ions are Cl (-), Br (-), Ho (-) they are Anions. The attractive forces between ions that are oppositely charged is described under the Coulomb’s Law, as the law says the force increases with charge and decreases as the distance between these ions increases. The highly polarised or charged nature of the ionic molecules is reflected in the nature of their melting point. For e.g. NaCl has a melting point of 801oc. The ionic molecules also show the property of high solubility in water.
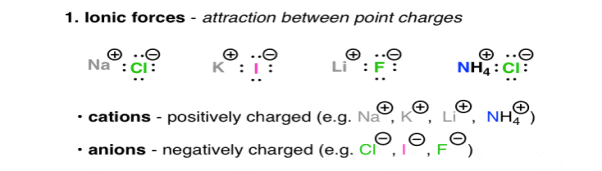
Fig. 1: Ionic forces – attraction between point charges
- Hydrogen bonding:
Hydrogen bonding occurs in molecules that are highly electromagnetic in nature, elements like F, O or N are directly bound to hydrogen. As hydrogen has an electronegativity of 2.2, they are not as polarized as ionic bonds and have some covalent character. But still the hydrogen bond is polarized and possess a dipole.
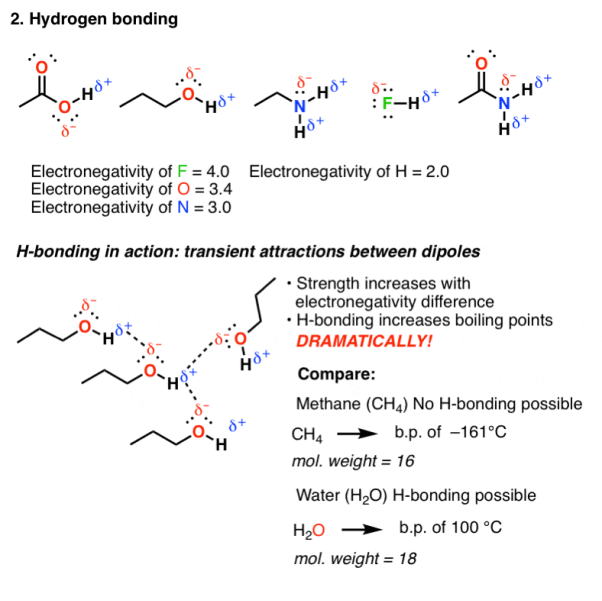
Fig. 2: Hydrogen bonding
Hydrogen bonding is an attractive interaction that occurs when the dipole of one molecule can align with the dipole from another molecule. Since the molecular motion of these molecules are rapid in a solution, these bonds are short lived therefore HO and NH are bonding molecules containing these functional groups that tend to have high boiling point.
- Van der Waals dipole- dipole interaction
Other groups other than hydrogen can be involved in covalent bonding with strong electronegative atoms. For example, in the figure given below each of the molecules contain a dipole:
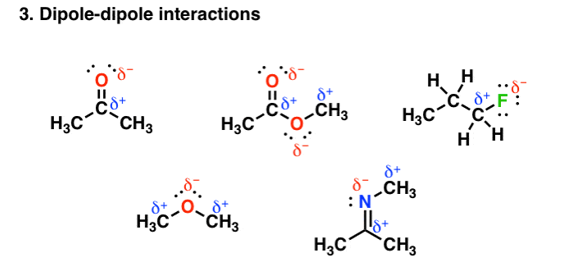
Fig. 3: Dipole-dipole interaction
- Dipoles are created by differences in electronegativities between nearby atoms
- Interactions between opposite-charged dipoles are attractive
- Similar in origin to hydrogen bonding, but since the differences in electronegativities are smaller
- Carbon is more electronegative (2.5) than hydrogen (2.2): the magnitudes of the dipoles are smaller, and these interactions are weaker.
These dipoles interact with each other in a very unique and attractive manner and thereby increase the boiling point. But the main aspect is the bonding depends on the electronegativity differences. The electronegativity of carbon =2.5, but that of Oxygen and Nitrogen is less than hydrogen whose electronegativity is=2.2, therefore the polar interaction is not so very strong. So, on an average these forces tend to be weaker than in hydrogen bonding
To sum up, boiling points are a measure of intermolecular forces and boiling point increases with molecular weight and surface area. The intermolecular forces increase with the increase in polarization of bonds.
The ideal gas law is one of the simplest equations of state, although it is accurate for gases at low pressure and high temperatures, but becomes relatively inaccurate at high pressure and low temperatures. The ideal gas law is used in various fields like science and engineering, due to its simple equation.
Ideal Gas Law: is an equation state of an ideal gas, it combines many gas laws together (Daltons law, Boyles law, Avogadro’s law)
P=Ρrt
Here p is the pressure of gas; is the density of the gas equal to m/V; m is the mass of the gas occupying volume V; V the volume it occupies, R the gas constant for the given gas; and T the temperature of the gas In SI units, the pressure is expressed in pascals, the volume in cubic meters, and the temperature in degrees Kelvin. The ideal gas law generalizes the three classical gas laws.
The equation is valid only for an ideal gas. Real gases obey this equation only approximately but its validity increases as the density of the gas tends to zero.
Ideal gas
Ideal gas (also called perfect gas) is a hypothetical gas which obeys the gas laws exacltly. An ideal gas consists of molecules which occupy negligible space and among which negligible forces exist, except at collisions. All collisions between molecules or between molecules and the wall of a container are perfectly elastic, as the molecules have no means of storing energy except as translational kinetic energy. Ideal gas is a good approximation for diluted real gases.
At lower temperatures and higher densities, it may be necessary to treat quantum-mechanical effects statistics even before those of interactions. In such cases, of an ideal gas is extended to that of an ideal Fermi gas or Bose gas.
Surfaces.
In a molecule, atoms are held together by chemical bonds, stretching or compressing occurs in bonds when bonds are distorted, thereby increasing the potential energy of its system. The molecule however remains stationary when a new geometry is formed. Therefore, the position of the atoms (potential)plays an important role in proving that the energy of the system is not caused by the kinetic energy, the position of the nuclei directly corresponds to the Energy of a molecule. The electrons however readjustquickly When nuclei show movement. Thus, the relationship between this molecular energy and molecular geometry (position) is mapped out with potential energy surface.
Three-dimensional PES is used for systems that have three atoms; in this case the collision reaction of an atom is substituted a diatomic molecule. The very first study done on this topic is H3H3 atom. The reaction is
H+H2→H2+H(2)(2)H+H2→H2+H
In this case, the triatomic molecule is the H-H-H transition state. There occurs a barrier on the potential energy surface at this point as it may have a higher energy than the product and reactants. Analysis such as the Quantum mechanical and quasiclassical trajectories calculations arerequired for the PES of H3 system. The PES howeverdoes not dependent on the masses of the atoms, therefore, the H3 surface in this reaction can be used for any isotopic variant. As three nuclei (ABC) are involved, the PES depends on three coordinates. Therefore, one coordinate needs to be fixed in order to plot the PES as a function of the remaining two.
The potential energy surface of H + H2 can be seen in figure below
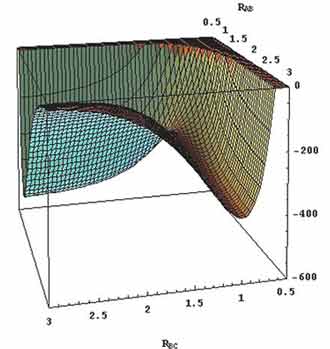
Fig 4: (Potential energy surface for the H3 (H+H2) system.

Fig 5: The nuclei (ABC), their transitions are marked in red cross and the contour plot represents the three-dimensional potential energy surfaces.
The barrier at the transition state is called the saddle point, it can be noticed thatanalong with a symmetric stretch a minimum coordinated, correspondingly a maximum along the asymmetric stretching coordinates.
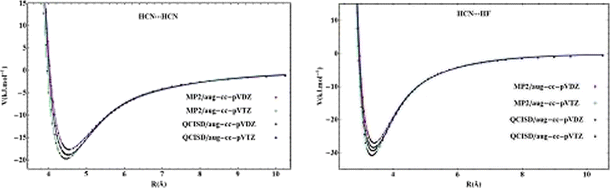
With elaborate work it was evaluated that, the potential energy surface which is one dimensional was used for calculating the spectroscopic properties (rovibrational constants and rotational line energies) of hydrogen bonds which are in linear bonded complexes and by comparing theoretical results with the corresponding experimental results. For this reason, two hydrogen bonded complexes are taken into consideration: the HCN···HCN homodimer and the HCN···HF heterodimer. In these complexes involving one-dimensional potential energy surfaces that are related to the hydrogen bonds in these complexes were calculated using different computational methods and basis sets. The calculated potential curve of each complex was fitted to an analytical one-dimensional potential function to obtain the potential parameters. The results obtained from each complex of analytical potential functionwas used in a two-particle Schrödinger equation in order to get the results of the rovibrational energy levels of the hydrogen bond. From the available experimental data from literature, the results of the rovibrational levels, the rovibrational spectra and constants of each complex compared. The results when compared showed that the one -dimensional potential energy surface predicted better results of the spectrotrophic properties of hydrogen bond better than the potential curve results obtained from other methods, especially for the HCN···HCN homodimer complex. Generally, the results obtained for the HCN···HCN homodimer complex were closer to experimental data than those obtained for the HCN···HF heterodimer complex. The elaborate work proved that the one-dimensional potential curve with respect to its hydrogen bond present between two linear molecules, can be used to predict the spectroscopic constants of hydrogen bonds.
Potential energy surface is obtained through the calculations for the H2F+ ion. 8 864 points are calculated within 20 000 cm−1 from the equilibrium configuration and fitted to the analytical expression used by Partridge and Schwenke in the case of the water molecule [J. Chem. Phys. 106 (1997) 4618–4639]. The points are reproduced with a root mean square deviation of 4.1 cm−1 using 48 parameters. When a three dimensional towards Vibrational energies are usedin calculations this yields more accurate fundamental for the ν2 and ν3 modes than previous calculations. Seven parameters including bond angle and bond length equilibrium values are used in the experimental data of the potential energy surface. The adjusted surface allows us to reproduce the available high-resolution experimental data with a root mean square deviation of 0.014 cm−1 up to J = 4. Vibrational energies are calculated up to 10 000 cm−1 and a line list is built up to J = 5 for transitions involving the eight first vibrational states.
Graphical abstract
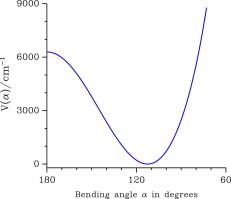
The three-dimensional potential energy surface of the astrophysical relevant H2F+ ion is obtained.
A global analysis of the available high-resolution data is performed.
The potential energy function for the bending mode is retrieved and is consistent with a low barrier to linearity of 6290 cm−1.
A line list of all transitions up to the second triad with J ⩽ 5 is built.
Reference:
- Gases, liquids and solids and other states of matter – 3rd Edition, D. Tabor
- Theory of Intermolecular forces 2nd Edition
- Intermolecular forces – Mrs. Shilpi Nagpal