UNIT 4
Sections and Sectional Views of Right Angular Solids
A solid has three dimensions, length, breadth and thickness. To represent a solid on a flat surface having only length and breadth, at least two orthographic views are necessary. Sometimes, additional views projected on auxiliary planes become necessary to make the description of a solid complete.
This chapter deals with the following topics:
1. Types of solids.
2. Projections of solids in simple positions.
(a) Axis perpendicular to the H.P.
(b) Axis perpendicular to the V.P.
(c) Axis parallel to both the H.P. And the V.P.
3. Projections of solids with axes inclined to one of the reference planes and
Parallel to the other.
(a) Axis inclined to the V.P. And parallel to the H.P.
(b) Axis inclined to the H.P. And parallel to the V.P.
4. Projections of solids with axes inclined to both the H.P. And the V.P.
5. Projections of spheres.
Types of solids:
Solids may be divided into two main groups:
(1) Polyhedra
(2) Solids of revolution.
Polyhedra: A polyhedron is defined as a solid bounded by planes called faces. When all faces are equal and regular, the polyhedron is said to be regular. There are seven regular Polyhedra which may be defined as stated below:
(i) Tetrahedron (fig. 1): It has four equal faces, each an equilateral triangle.
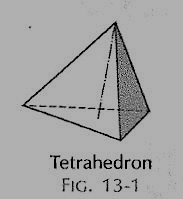
Figure 1
(ii) Cube or hexahedron (fig. 2): It has six faces, all equal squares.
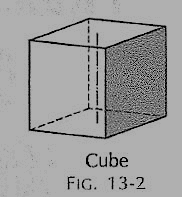
Figure 2
(iii) Octahedron (fig. 3): It has eight equal equilateral triangles as faces.
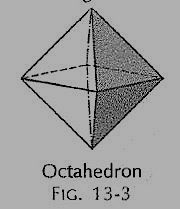
Figure 3
(iv)Dodecahedron (fig. 4): It has twelve equal and regular pentagons as faces.
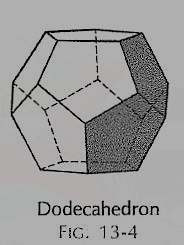
Figure 4
(v) Icosahedron (fig. 5): It has twenty faces, all equal equilateral triangles.

Figure 5
(vi)Prism: This is a polyhedron having two equal and similar faces called its ends or bases, parallel to each other and joined by other faces which are parallelograms. The imaginary line joining the centers of the bases is called the axis. A right and regular prism (fig. 6) has its axis perpendicular to the bases. All its faces are equal rectangles.
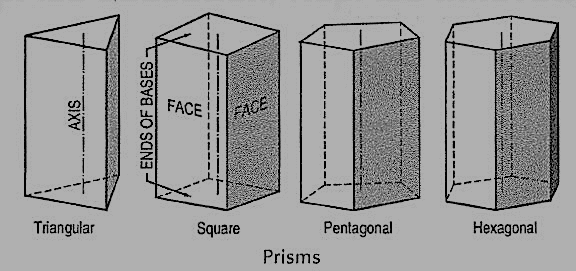
Figure 6
(vii) Pyramid: This is a polyhedron having a plane figure as a base and many triangular faces meeting at a point called the vertex or apex. The imaginary line joining the apex with the centre of the base is its axis.
A right and regular pyramid (fig. 7) has its axis perpendicular to the base which is a regular plane figure. Its faces are all equal isosceles triangles.
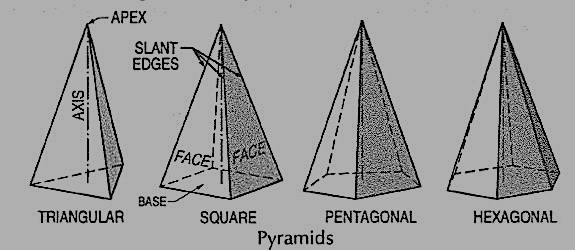
Figure 7
Oblique prisms and pyramids have their axes inclined to their bases. Prisms and pyramids are named according to the shape of their bases, as triangular, square, pentagonal, hexagonal etc.
Solids of revolution
(i) Cylinder (fig. 8): A right circular cylinder is a solid generated by the revolution of a rectangle about one of its sides which remains fixed. It has two equal circular bases. The line joining the centers of the bases is the axis. It is perpendicular to the bases.
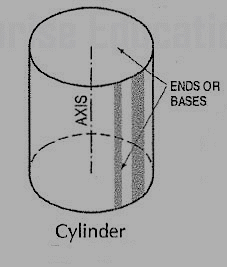
Figure 8
(ii) Cone (fig. 9): A right circular cone is a solid generated by the revolution of a right-angled triangle about one of its perpendicular sides which is fixed.
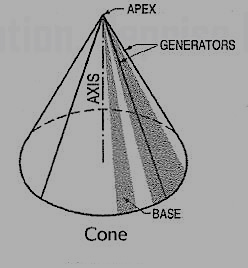
Figure 9
It has one circular base. Its axis joins the apex with the centre of the base to which it is perpendicular. Straight lines drawn from the apex to the circumference of the base-circle are all equal and are called generators of the cone. The length of the generator is the slant height of the cone.
Invisible features of an object are shown by dotted lines in their projected views. But when such features are too many, these lines make the views more complicated and difficult to interpret. In such cases, it is customary to imagine the object as being cut through or sectioned by planes. The part of the object between the cutting plane and the observer is assumed to be removed and the view is then shown in section.
The imaginary plane is called a section plane or a cutting plane. The surface produced by cutting the object by the section plane is called the section. It is indicated by thin section lines uniformly spaced and inclined at 45°.
The projection of the section along with the remaining portion of the object is called a sectional view. Sometimes, only the word section is also used to denote a sectional view.
(1) Section planes:
Section planes are generally perpendicular planes. They may be perpendicular to one of the reference planes and either perpendicular, parallel or inclined to the other plane. They are usually described by their traces. It is important to remember that the projection of a section plane, on the plane to which it is perpendicular, is a straight line. This line will be parallel, perpendicular or inclined to xy, depending upon the section plane being parallel, perpendicular or inclined respectively to the other reference plane.
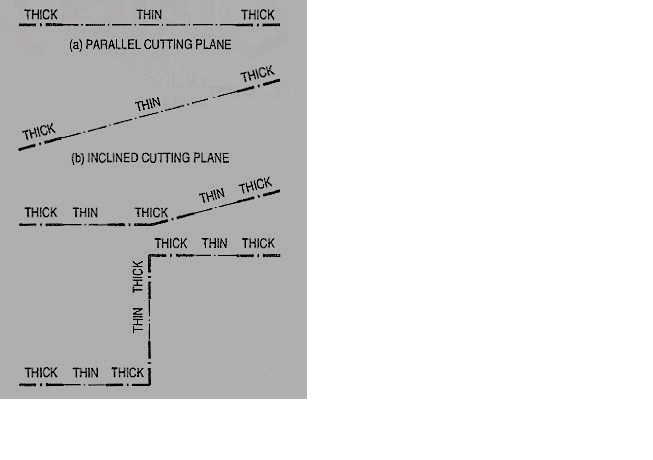
As per latest 8.1.S. Convention (SP: 46-2003), the cutting-plane line should be drawn as shown in fig. 1.
(2) Sections: The projection of the section on the reference plane to which the section plane is perpendicular, will be a straight-line coinciding with the trace of the section plane on it. Its projection on the other plane to which it is inclined is called apparent section. This is obtained by
(i) Projecting on the other plane, the points at which the trace of the section plane intersects the edges of the solid and
(ii) Drawing lines joining these points in proper sequence.
(3) True shape of a section: The projection of the section on a plane parallel to the section plane will show the true shape of the section. Thus, when the section plane is parallel to the H.P. Or the ground, the true shape of the section will be seen in sectional top view. When it is parallel to the V.P., the true shape will be visible in the sectional front view.
But when the section plane is inclined, the section must be projected on an auxiliary plane parallel to the section plane, to obtain its true shape. When the section plane is perpendicular to both the reference planes, the sectional side view will show the true shape of the section. In this chapter sections of different solids are explained in stages by means of typical problems as follows:
1. Sections of prisms
2. Sections of pyramids
3. Sections of cylinders
4. Sections of cones
5. Sections of spheres.
Imagine that a solid is enclosed in a wrapper of thin material, such as paper. If this covering is opened out and laid on a flat plane, the flattened-out paper is the development of the solid. Thus, when surfaces of a solid are laid out on a plane, the figure obtained is called its development.
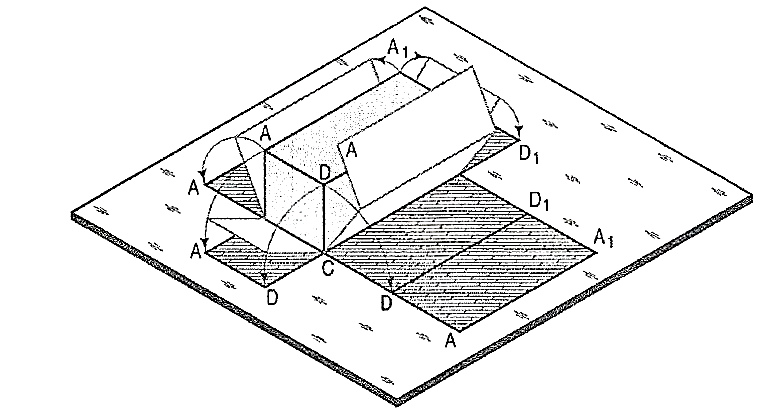
Figure 4.2.1
Fig. 4.2.1 shows a square prism covered with paper in process of being opened out. Its development (fig. 4.2.2) consists of four equal rectangles for the faces and two similar squares for its ends. Each figure shows the true size and shape of the corresponding surface of the prism. The development of a solid, thus represents the actual shape of all its surfaces which, when bent or folded at the edges, would form the solid.
Hence, it is very important to note that every line on the development must be the true length of the corresponding edge on the surface.
The knowledge of development of surfaces is essential in many industries such as automobile, aircraft, ship building, packaging and sheet-metal work. In construction of boilers, bins, process-vessels, hoppers, funnels, chimneys etc., the plates are marked and cut according to the developments which, when folded, form the desired objects. The form of the sheet obtained by laying all the outer surfaces of the solid with suitable allowances for the joints is known as pattern.
Only the surfaces of polyhedral (such as prisms and pyramids) and single curved surfaces (as of cones and cylinders) can be accurately developed. Warped and double-curved surfaces are undevelopable. These can however be approximately developed by dividing them up into many parts.
This chapter deals with the following topics:
1. Methods of development.
2. Developments of lateral surfaces of right solids.
3. Development of transition pieces.
4. Spheres (approximate method).
The following are the principal methods of development:
1. Parallel-line development:
It is employed in case of prisms and cylinders in which stretch-out-line principle is used. Lines A-A and A1-A1in fig.2 are called the stretch-out Ines.
2. Radial-line development:
Itis used for pyramids and cones in which the true length of the slant edge or the generator is used as radius.
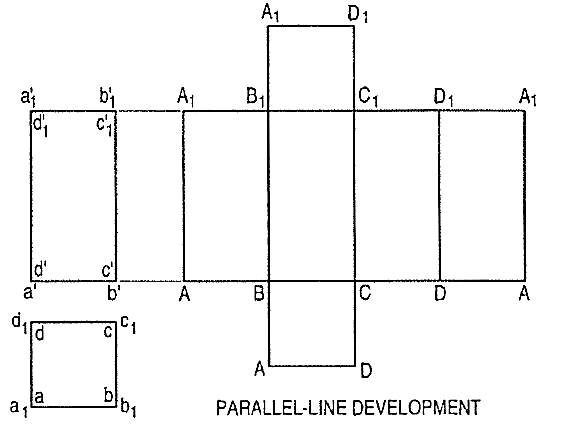
Figure 4.2.2
3. Triangulation development:
This is used to develop transition pieces. This is simply a method of dividing a surface into many triangles and transferring them into the development.
4. Approximate method:
It is used to develop objects of double curved or warped surfaces as sphere, paraboloid, ellipsoid, hyperboloid and helicoid.
Developments of lateral surfaces of right solids:
The methods of drawing developments of surfaces of various solids are explained by means of the following typical problems. Only the lateral surfaces of the solids (except the cube) have been developed. The ends or bases have been omitted. They can be easily incorporated if required.
Cube
The development of the surface of a cube consists of six equal squares, the length of the side of the squares being equal to the length of the edge of the cube.
Problem:
1. Draw the development of the surface of the part P of the cube, the front view of which is shown in fig. 4.2.3(i) Name all the corners of the cube and the points at which the edges are cut.
(i) Draw the stretch-out lines A-A and E-E directly in line with the front view, and assuming the cube to be whole, draw four squares for the vertical faces, one square for the top and another for the bottom as shown in fig. 4.2.3(ii).
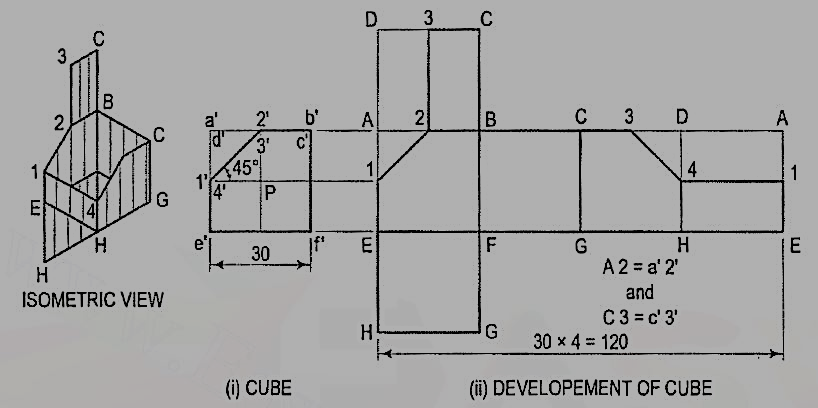
Figure 4.2.3
(ii) Name all the corners. Draw a horizontal line through 1' to cut AE at 1 and DH at 4. a' b' is the true length of the edge. Hence, mark a point 2 on AB and 3 on CD such that A 2 = a' 2' and C 3 = c' 3'. Mark the point3 on CD in the top square also.
(iii) Draw lines 1-2, 2-3, 3-4 and 4-1, and complete the development as shown. Keep lines for the removed portion, viz. A1, A2, 3D, D4 and DA thin and fainter.
2. Draw the development of the surface of the part P of the cube shown in two views in fig. 4.2.4(i).
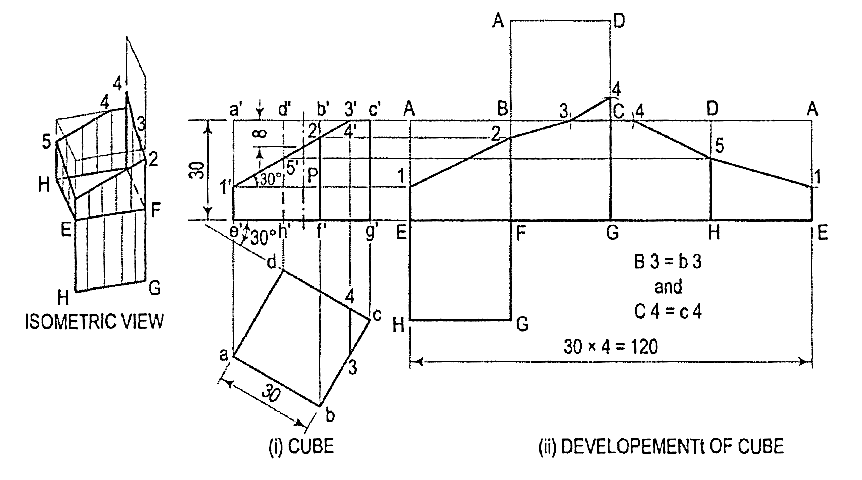
Figure 4.2.4
(i) Draw horizontal lines through points 1 ', 2' and 5' to cut AE in 1, BF in 2and DH in 5 respectively. Lines b'c' and c'd' do not show the true lengths of the edges. The sides of the square in the top view show the true length. Therefore, mark points 3 in BC and 4 in CD such that 83 = b3 and C4 = c4.
(ii) Draw lines joining 1, 2, 3 etc. in correct sequence and complete the required development. Keep the lines for the removed part fainter.
Prisms:
Development of the lateral surface of a prism consists of the same number of rectangles in contact as the number of the sides of the base of the prism. Oneside of the rectangle is equal to the length of the axis and the other side equalto the length of the side of the base.
Problem:
3. Draw the development of the lateral surface of the part P of the pentagonal prism shown in fig. 4.2.5 (i).
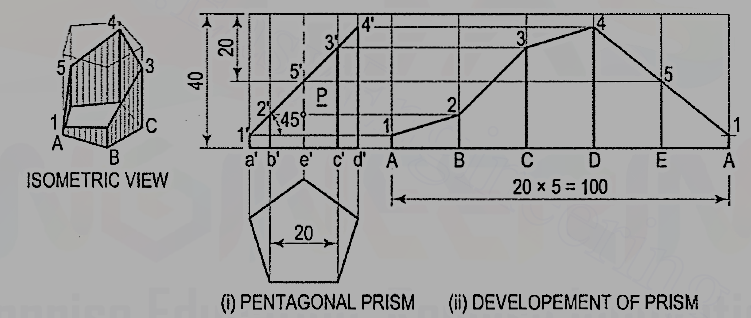
Figure4.2.5
Name the corners of the prism and the points at which the edges are cut.
(i) Draw the development assuming the prism to be whole [fig. 4.2.5(ii)]. It is made up of five equal rectangles.
(ii) Draw horizontal lines through points 1’, 2’ etc. to cut the lines for the corresponding edges in the development at points 1, 2 etc.
(iii)Draw lines joining these points and complete the development as shown.
4. Draw the development of the lateral surface of the part P of the hexagonal prism shown in fig. 4.2.6 (i).
Name the points at which the edges are cut and draw the development assuming the prism to be whole [fig. 4.2.6(ii)].
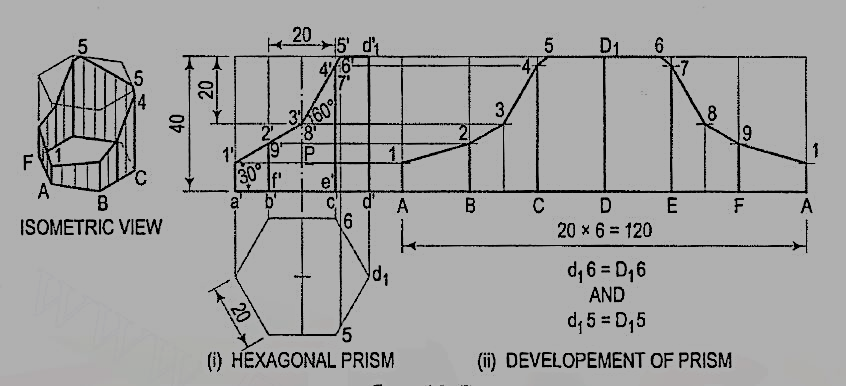
Figure 4.2.6
(i) Obtain all the points except 5 and 6 by drawing horizontal lines. Note that points 3 and 8 lie on vertical lines drawn through the mid-points of BC and EF.
(ii) Mark points 5 and 6 such that SD1 = 5d1 and D16 = d16.
(iii) Draw lines joining points 1, 2, 3 etc. in correct sequence and complete the required development as shown.
Cylinders
The development of the lateral surface of a cylinder is a rectangle having one side equal to the circumference of its base-circle and the other equal to its length.
Problem
1. Develop the lateral surface of the truncated cylinder shown in fig. 4.2.7(i).
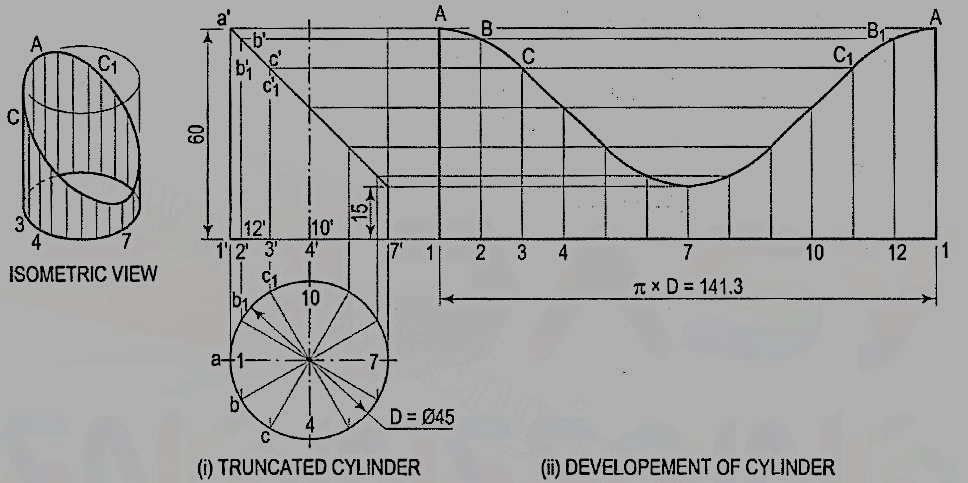
Figure 4.2.7
(i) Divide the circle in the top view into twelve equal parts. Project the division points to the front view and draw the generators. Mark points a', b' andb'1, c' and c'1 etc. in which the generators are cut.
(ii) Draw the development of the lateral surface of the whole cylinder along with the generators [fig. 4.2.7(ii)]. The length of the line 1-1 is equal to π x D (circumference of the circle). This length can also be marked approximately by stepping off with a bow divider, twelve divisions, each equal to the chord-length ab. (The length thus obtained is about 1 %shorter than the exact length; but this is permitted in drawing work.)
(iii) Draw horizontal lines through points a', b' and b'1 etc. to cut the corresponding generators in points A, B and B1 etc. Draw a smooth curve through the points thus obtained. The figure 1-A-A-1 is the required development.
Pyramids
The development of the lateral surface of a pyramid consists of many equal isosceles triangles in contact. The base and the sides of each triangle are respectively equal to the edge of the base and the slant edge of the pyramid.
Method of drawing the development of the lateral surface of a pyramid:
(i) With any point O as centre and radius equal to the true length of the slant edge of the pyramid, draw an arc of the circle. With radius equal to the true length of the side of the base, step-off (on this arc) the same number of divisions as the number of sides of the base.
(ii) Draw lines joining the division-points with each other in correct sequence and with the centre for the arc. The figure thus formed (excluding the arc) is the development of the lateral surface of the pyramid.
Problem:
1. Draw the development of the lateral surface of the part P of the triangular pyramid shown in fig. 4.2.8 (i). The line o'1' in the front view is the true length of the slant edge because it is parallel to xy in the lop view. The true length of the side of the base is seen in the top view.
(i) Draw the development of the lateral surface of the whole pyramid [fig. 8(ii)]as explained above. On 01 mark a point A such that OA = o'a'. o'2' (with which o'3' coincides) is not the true length of the slant edge.
(ii) Hence, through b', draw a line parallel to the base and cutting o' a' at b".o'b" is the true length of o'b' as well as o'c'. Mark a point B in 02 and C in 03 such that OB = OC = o'b".
(iii) Draw lines AB, BC and CA and complete the required development as shown. Keep the arc and the lines for the removed part fainter.
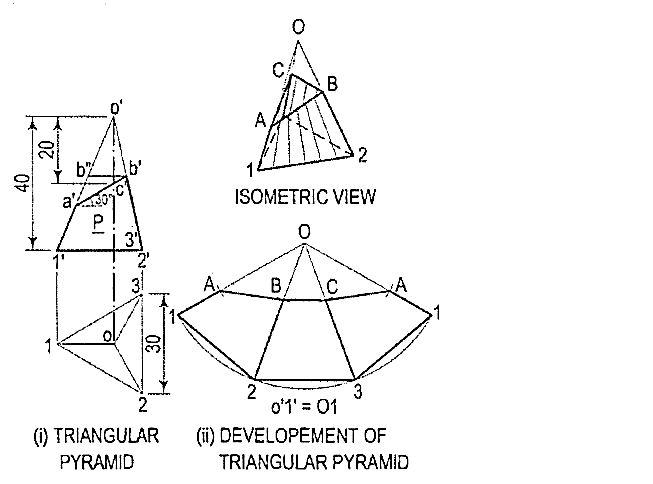
Figure 4.2.8
2. Draw the development of the lateral surface of the frustum of the square pyramid shown in fig. 4.2.9 (i).
(i) Determine the position of the apex. None of the lines in the front view shows the true length of the slant edge. Therefore, draw the top view and make any one line (for the slant edge) horizontal, i.e. parallel to xy and determine the true length o'1 '1. Through a', draw a line parallel to the base and obtain the true length o'a".
(ii) With O as centre and radius o'1 '1, draw an arc and obtain the development of the lateral surface of the whole pyramid [fig. 4.2.9(ii)].
(iii) With centre O and radius o' a", draw an arc cutting O1, O2 etc. at points A, B etc. respectively.
(iv) Draw lines AB, BC, CD and DA and complete the required development. Note that these lines are respectively parallel to lines 1-2, 2-3 etc.

Figure 4.2.9
3.A frustum of a square pyramid has its base 50 mm side; top 25 mm side and height 75 mm. Draw the development of its lateral surface.
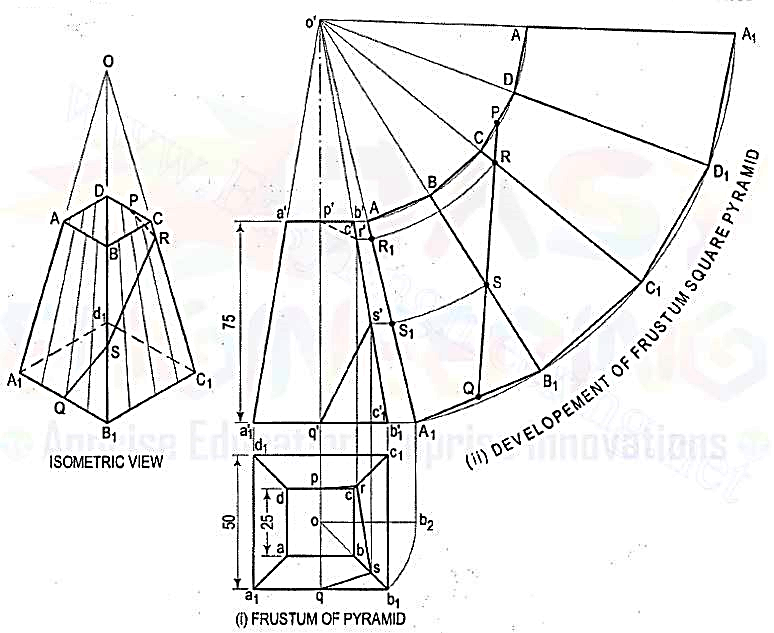
Figure 4.2.10
(i) Mark the mid-point P of CD and Q of A1B1. Draw a line joining P and Q and cutting CC1 at R and BB1 at S. Transfer these points to the front view and the top view. For example, with o' as centre and radius o'R, draw an arc cutting o' A1 at R1. Through R1, draw a line parallel to the base and cutting c'c'1 at r'. Project r' to r on cc1 in the top view. r' and r are the projections of R.
(ii) Similarly, obtain s' and s on b'b'1 and bb1 respectively. Draw lines pr, rs and sq which will show the top view of the line PQ. p'r's'q' will be the path of the line PQ in the front view.
Cone
The development of the curved surface of a cone is a sector of a circle, the radius and the length of the arc of which are respectively equal to the slant height and the circumference of the base-circle of the cone.
Problem:
1. Draw the development of the lateral surface of the truncated cone shown in fig. 4.2.11 (i).
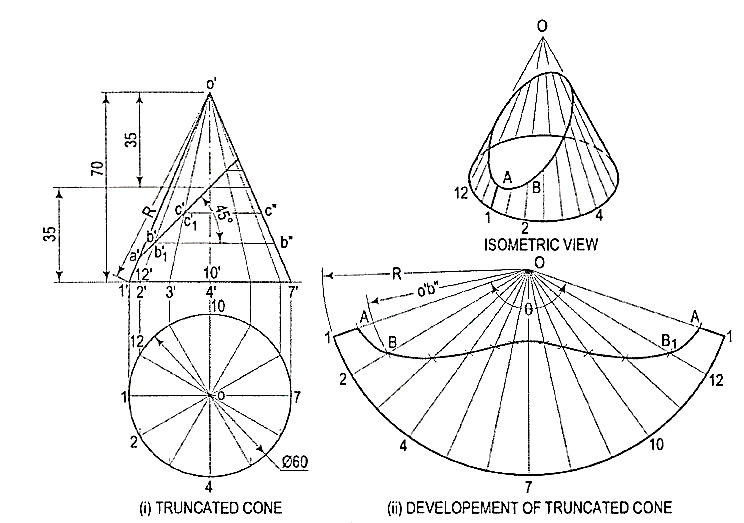
Figure 4.2.11
Assuming the cone to be whole, let us draw its development.
(i) Draw the base-circle in the top view and divide it into twelve equal parts.
(ii) With any point O as centre and radius equal to o'1' or o'7', draw an arc of the circle [fig. 15-24(ii)]. The length of this arc should be equal to the circumference of the base circle. This can be determined in two ways.
(iii) Calculate the subtended angle θ by the formula,
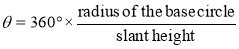
Cut-off the arc so that it subtends the angle θ at the center and divide it into twelve equal parts.
(iv) Step-off with a bow-divider, twelve equal divisions on the arc, each equal to one of the divisions of the base-circle.
(This will give an approximate length of the circumference. Note that the base-circle should not be divided into less than twelve equal parts.)
(v) Join the division-points with 0, thus completing the development of the whole cone with twelve generators shown in it [fig. ,11(ii)].
(vi) The truncated portion of the cone may be deducted from this development by marking the positions of points at which generators are cut and then drawing a curve through them. For example- generators o'2' and o'12' in the front view are cut at points b' and b'1 which coincide with each other. The true length ofo' b' may be obtained by drawing a line through b', parallel to the base and cutting o'7' at b". Then o'b" is the true length of o'b'.
(vii) Mark points B and 81 on generators 02 and 0-12 respectively, such that OB = 0B1 = o' b". Locate all points in the same way and draw a smooth curve through them. The figure enclosed this curve and the arc is the development of the truncated cone.
2. Draw the development of the lateral surface of the part P of the cone shown in fig. 4.2.12
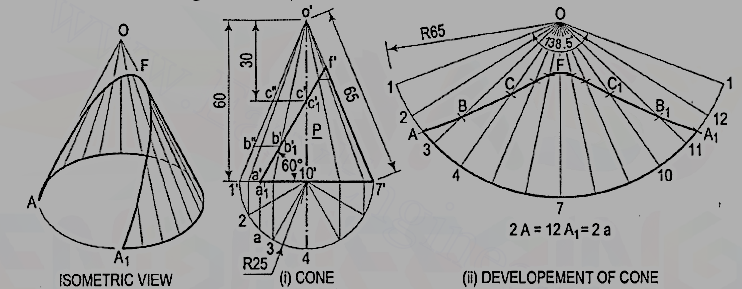
Figure 4.2.12
Draw the development as explained in problem [fig. 4.2.12 (ii)]. For the points at which the base of the cone is cut, mark points A and A1 on the arcs2-3 and 11-12 respectively, such that A2 = A1 12 = a2. Draw the curve passing through the points A, B, C etc. The figure enclosed between this curve and the arcA-A1 is the required development.
3. Draw the projections of a cone resting on the ground on its base and show on them, the shortest path by which a point P, starting from a point on the circumference of the base and moving around the cone will return to the same point. Base of cone 61 mm diameter; axis 75 mm long.
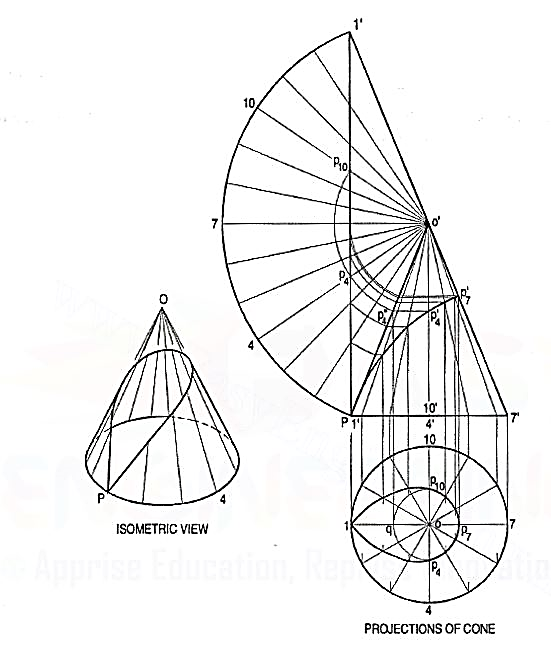
Figure 4.2.13
(i) Draw the projections and the development of the surface of the cone showing all twelve generators (fig. 4.2.13). The development may be drawn attached to o'1 '.
(ii) Assume that P starts from the point 1 (i.e. point 1' in the front view).Draw a straight line 1 '1' on the development. This line shows the required shortest path. Let us take a point P4 at which the path cuts the generator o’4. Mark a point P"4 on o'1' such that o'P"4 = o'P4. This can be done by drawing an arc with o' as centre and radius equal to o'P 4 cutting o11'at P"4. Through P"4, draw a line parallel to the base cutting o'4' at P'4.Then p'4 is the position of the point p4 in the front view. Similarly, transfer all the points to the front view and draw the required curve through them. The curve at the back will coincide with the front curve.
(iii) Project these points to the top view on the respective generators. p'4 andp'10 cannot be projected directly. Hence, project p"4 to a point q on o1.With o as centre and radius equal to oq, draw an arc cutting o4 at p4 ando-10 at p10. Thus op4 = op10 = oq. A curve drawn through the points thus obtained will show the path in the top view.
Conversion of a pictorial view into orthographic views requires sound knowledge of the principles of pictorial projection and some imagination. A pictorial view may have been drawn according to the principles of isometric or oblique projection. In either case, it shows the object as it appears to the eye from one direction only. It does not show the real shapes of its surfaces or the contour. Hidden parts and constructional details are also not clearly shown. All these must be imagined.
For converting a pictorial view of an object into orthographic views, the direction from which the object is to be viewed for its front view is generally indicated by means of an arrow. When this is not done, the arrow may be assumed to be parallel to a sloping axis. Other views are obtained by looking in directions parallel to each of the other two axes and placed in correct relationship with the front view.
When looking at the object in the direction of any one of the three axes, only two of the three overall dimensions (viz. Length, height and depth or thickness) will be visible. Dimensions which are parallel to the direction of vision will not be seen. Lines which are parallel to the direction of vision will be points, while surfaces which are parallel to it will be lines.
While studying a pictorial view, it should be remembered that, unless otherwise specified:
(i) A hidden part of a symmetrical object should be assumed to be like the corresponding visible part.
(ii) All holes, grooves etc. should be assumed to be drilled or cut right through.
(iii) Suitable radii should be assumed for small curves of fillets etc. An object in its pictorial view may sometimes be shown with a portion cut and removed, to clarify some internal constructional details. While preparing its orthographic views, such object should be assumed to be whole, and the views should then be drawn as required.
Orthographic projection
(i) It is comparatively easy to prepare a drawing from an actual object. The object is carefully examined and then placed in a suitable position for the front view. The front view of the object is selected in such a way that the maximum details of the object are visible so that the minimum dotted lines are required.
(ii) All the necessary views are then sketched freehand in a sketch book or on a pad.
(iii) Measurements of all its details and overall sizes are taken and inserted in the views, along with important notes and instructions.
(iv) Finally, a scale-drawing is prepared from these sketches.
A pictorial view of a rectangular plate is given in fig. 4.3.1(i). Its front view when seen in the direction of the arrow X, side view from the left, i.e. in the direction of the arrow Y and the top view in the direction of arrow Z, are shown in fig.4.3.1(ii).
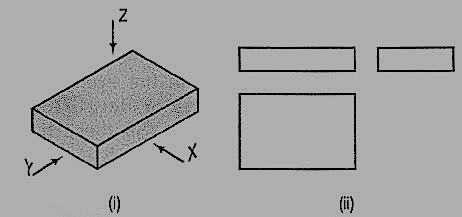
Figure 4.3.1
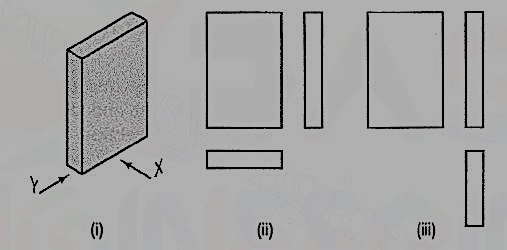
Figure 4.3.2
The same plate is shown in fig. 4.3.2 (i) with its longer edges vertical. Its front view looking in the direction of the arrow X, side view from the left and the top view are shown in fig. 4.3.2 (ii). These three views are similar in shape and size to the views shown in fig. 4.3.1 (ii). Only their positions and conditions have changed. Even when the front view is drawn looking in the direction of the arrow Y [fig. 4.3.2 (iii)], the three views remain similar in shape and size.
The same plate is shown cut in various shapes in fig. 4.3.3. The front view and the side view in each case will be the same as in fig. 4.3.1 (ii). The changed shapes will be seen in the top view of each plate. If these plates are kept in the position shown in fig. 4.3.2 (i), the front view in each case (looking in direction of the arrow X) will show a different shape, while the side view and the top view will be rectangles.
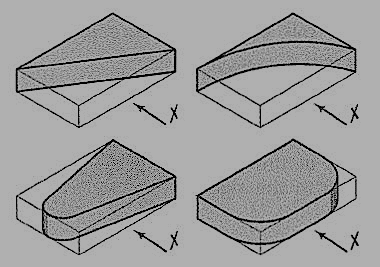
Figure 4.3.3
A plate cut in three different ways is shown in fig. 4.3.3. The front view in each case is the same, viz. a rectangle with a vertical line ab for the edge AB. The side view from the right in each case will be a rectangle with a vertical line cd for the edge CD. The top view in each case shows the shape of the cut.
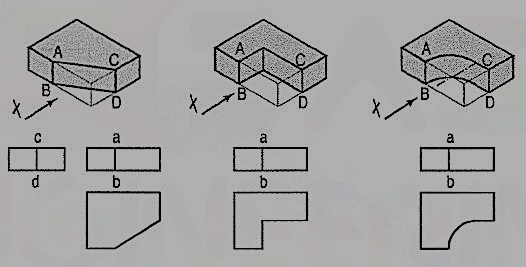
Figure 4.3.4
In the front view of the plate having different shapes of grooves (fig. 4.3.5), two vertical lines are drawn for the edges of rectangular as well as semi-circular grooves.
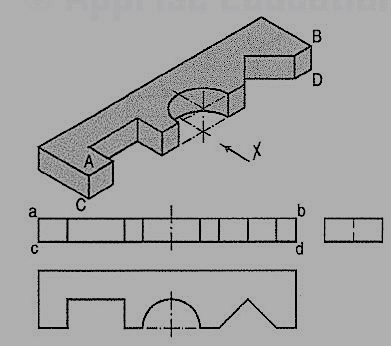
Figure 4.3.5
In case of the triangular groove, three vertical lines are required. Although edges AB and CD are cut, they are continuous lines ab and ed. In the top view, shapes of the grooves are seen. The grooves are not visible in the side view and hence, they are shown by a hidden line.
Two plates having grooves in upper and lower surfaces are shown in fig. 54. The shapes of the grooves are seen in the front views. In top views, two lines for the edges of rectangular as well as semi-circular grooves are drawn. For the triangular grooves, three lines are required. The tapered groove in the bottom surface is assumed to be cut throughout the width of the plate. It is not visible from above and hence; its four edges are shown by four hidden lines in the top view. In their side views, each groove should be shown by a horizontal hidden line. Therefore, the side view in this case is not necessary.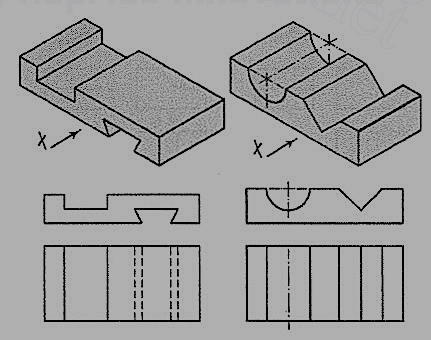
Figure 4.3.6
A plate having holes of different shapes is shown in fig. 4.3.6. These shapes are seen in the top view. Holes are assumed to be cut or drilled right through. They are shown by hidden lines in the front and the side views. Here also the right-side view is not necessary.
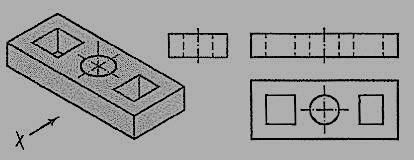
Figure 4.3.7
The semi-circular groove in the block shown in fig.4.3.7 does not extend up to the opposite surface. Therefore, although the edge AB is broken, ab is a continuous line in the front view. The groove is shown by hidden lines in the side view. In the top view it is drawn as a rectangle.
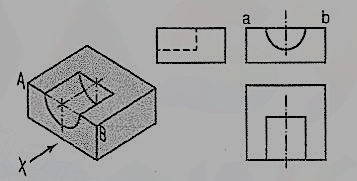
Figure 4.3.8
Fig. 4.3.8 shows a block in the shape of steps, along with its three views. In fig. 4.3.9, its face ABCD is inclined. Hence, in the top view, two lines ab and cd are drawn for that face.
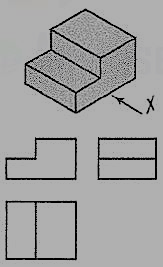
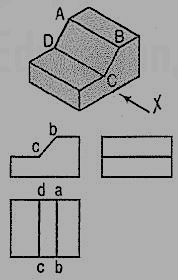
Figure 4.3.9
The front and back faces of the upper step are shown inclined in fig. 4.3.8. Their inclinations are shown in the side view. In the front view, the line pq for the edge PQ is drawn. In the top view, lines ef and gh for edges ff and CH are shown.
In fig. 4.3.9, all the four side-faces of the upper step are inclined. Their inclinations are seen in the front view and in the side view. In the top view, two rectangles are seen for the upper step. Lines (for the four sloping edges) joining the corners of the rectangles should also be shown.
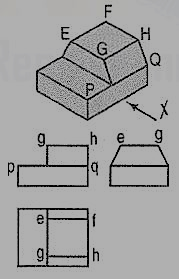

Figure 4.2.11
A casting having a hollow cylinder supported by a vertical rib is shown in fig. 4.2.11. The width of the rib is equal to the diameter of the cylinder. Hence, in the front view, vertical lines for the rib are tangential to the circle for the cylinder.
In the side view, the line showing the thickness of the rib vanishes just at the centre line. The rib is not visible when seen from top. Hence, it is shown by a hidden line in the top view. Note that the third view (top view) is a 'necessary' view to show the shape of rectangular slot.
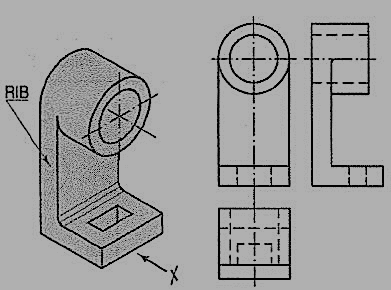
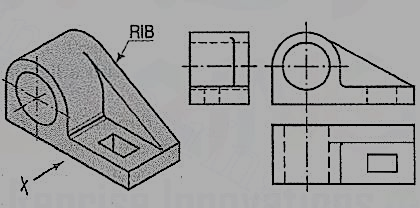
Figure 4.2.12
In the bearing block shown in fig. 4.2.12, the line for the rib is inclined and tangent to the semi-circle in the front view. Vanishing points for the lines for the rib in the side view and the top view are obtained by projecting the tangent-point from the front view.
From the above discussion, the following important points are to be noted:
(i) An object can be observed from six sides such as
(a) front side
(b) back side
(c) left-hand side
(d) right-hand side
(e) top side and
(f) bottom side.
It is not necessary to draw all the possible six views to describe completely the shape of the object. In practice, only those views which are necessary to describe the shape of the object should be drawn.
The view should be selected in such a way that minimum dotted lines are necessary to show internal details. The object which has both the right-hand side and left-hand side symmetrical shape requires only two views.
One of the views must be such that it completely describes the shape of the object. Refer fig. 4.3.13
(ii) Three views are necessary for the object which is not symmetrical. Refer fig. 58 and fig. 4.3.13.
(iii) The view should not be drawn out of place. That is the side view and top view are not aligned with the front view. This should be avoided.
(iv) Dotted lines must be drawn correctly as shown in table 1. Incorrect points are indicated by circle.
Table 1
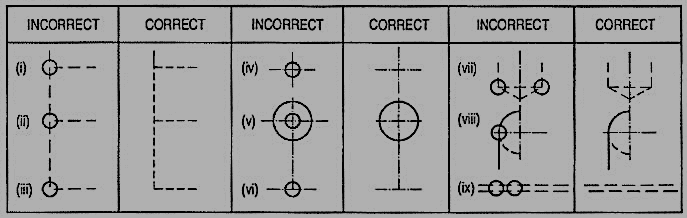
(v) (a) When a visible line coincides with either a dotted line or a centre line, the visible line is shown and a centre line is extended beyond the outlines of the view.
(b) When a section-plane line coincides with a centre line, the centre line is shown and the section-plane line is drawn outside the out-lines of the object at the ends of centre line by thick dashes.
(c) When a dotted line coincides with the centre line, the dotted line should be shown.
Machine element parts:
1.
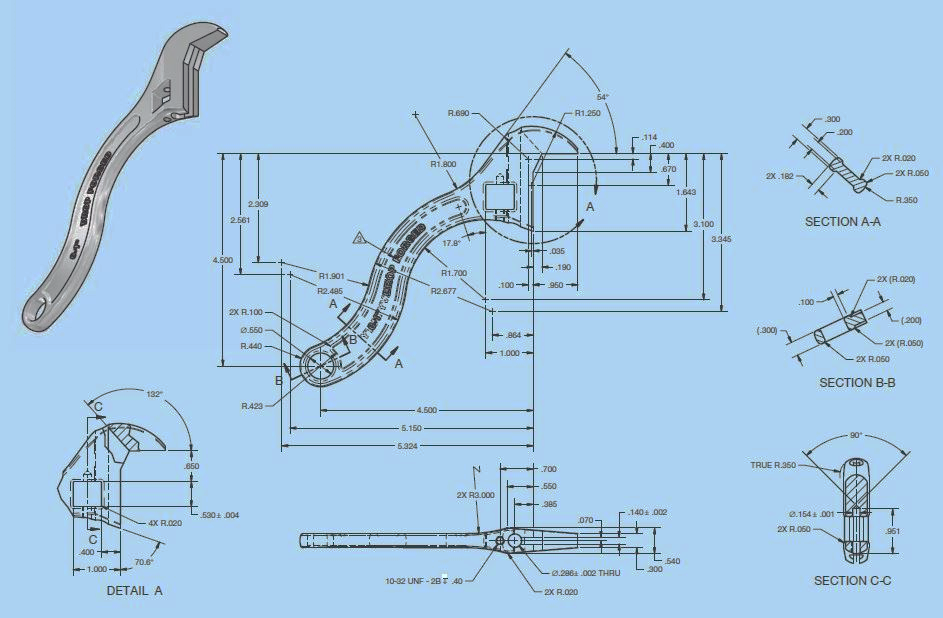
2. 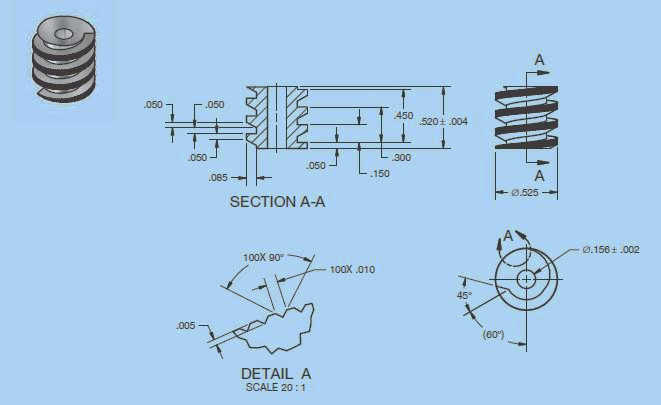
3.