UNIT–1

Calculus

1.1 Rolle’s theorem

Important definitions-

Continuity- suppose that a function f(x) is defined in the interval I , then it is said to be continuous at x=a ,  if

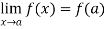
Differentiability- A function f(x) is said to be differentiable at x=a if

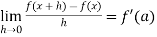exists      where ‘a’ belongs to I

Rolle’s theorem-

Suppose f(x) is a function defined on [a , b] and it satisfies the following conditions

1. f(x) is continuous in [a , b]

2. f(x) is differentiable in (a , b)

3. f(a) = f(b)

Then there exists atleast a point point c ϵ (a , b) , where a<b , such that f’(c) = 0

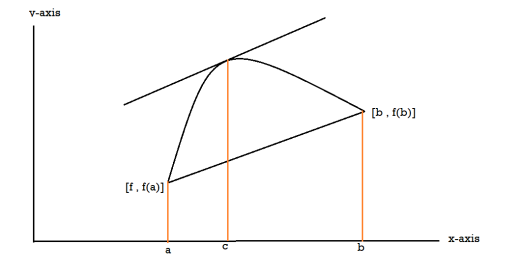
Proof: suppose y = f(x) is a function and A(a , f(a)) , B(b , f(b)) be two points on the curve f(x) and a,b are two end points. Now conditions for Rolle’s theorem-

1. f(x) is a continuous function in[a , b] , from the figure without breaks in between  A&B on y = f(x).

2. f(x) is differentiable in (a , b), because joining A and B we get a line AB.

Slope of the line AB=0 then a point C at P also a tangent at P, or Q,R,S is parallel to x –axis.

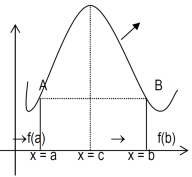
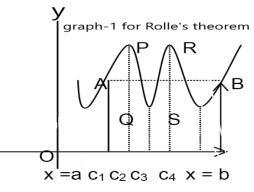
Slope of the tangent at P or Q,R,S , will be 0 ,even the curve y = f(x) decreases or increases, that means f(x) is constant.

Derivative of f(x),

f’(c) = 0

That’s why,     f’(c) = 0

3. The slope of the line AB is equal to zero, that means the line AB is parallel to x-axis.

So that,       f(a) = f(b)

Example 1

Verify Rolle’s theorem for the function f(x) = x2 for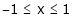

Solution:

Here f(x) = x2;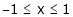

i)      Since f(x) is algebraic polynomial which is continuous in [-1, 1]

Ii)    Consider f(x) = x2

Diff. w.r.t. x we get

f'(x) = 2x

Clearly f’(x) exists in (-1, 1) and does not becomes infinite.

Iii)  Clearly

f(-1) = (-1)2 = 1

f(1) = (1)2 = 1

f(-1) = f(1).

Hence by Rolle’s theorem, there exist 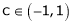such that

f’(c) = 0

i.e. 2c = 0

c = 0

Thus such that

f'(c) = 0

Hence Rolle’s Theorem is verified.

Example 2   Verify Rolle’s Theorem for the function f(x) = ex(sin x – cos x) in

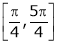
Solution:

Here f(x) = ex(sin x – cos x);

i)      Ex is an exponential function continuous for every 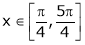also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in 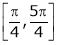and Hence ex(sin x – cos x) is continuous in .

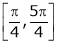Ii)    Consider

f(x) = ex(sin x – cos x)

Diff. w.r.t. x we get

f’(x) = ex(cos x + sin x) + ex(sin x + cos x)

= ex[2sin x]

Clearly f’(x) is exist for each 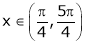& f’(x) is not infinite.

Hence f(x) is differentiable in .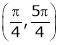

Iii)  Consider

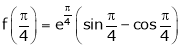
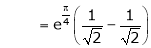
Also,

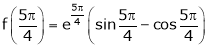
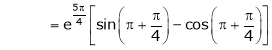
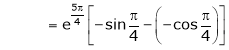
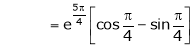
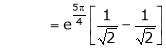
Thus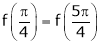

Hence all the conditions of Rolle’s theorem are satisfied, so there exist 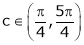such, that

i.e.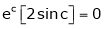

i.e. sin c = 0

But

Hence Rolle’s theorem is verified.

Example-3

Verify whether Rolle’s theorem is applicable or not for

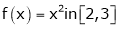
Solution:

Here f(x) = x2;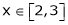

i)      X2 is an algebraic polynomial hence it is continuous in [2, 3]

Ii)    Consider

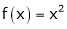
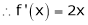
F’(x) exists for each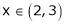

Iii)  Consider

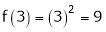
Thus .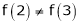

Thus all conditions of Rolle’s theorem are not satisfied Hence Rolle’s theorem is not applicable for f(x) = x2 in [2, 3]

Example-4:

Example: Verify Rolle’s theorem for the given functions below-

1.  f(x) = x³ - 6x²+11x-6  in the interval [1,3]

2. f(x) = x²-4x+8  in the interval [1,3]

Sol. (1)

As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]

Also, f(1) = f(3) = 0

Now we find f’(x) = 0

3x² - 12x +11 = 0

We get, x = 2+ 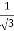and 2 -

Hence both of them lie in (1,3).

Hence the theorem holds good for the given function in interval [1,3]

(2) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]

Also,  f(1) = 1 -4 +8 = 5 and f(3) = 9 – 12 + 8 = 5

Hence f(1) = f(3)

Now the first derivative of the function,

f’(x) = 0

2x – 4 = 0 , gives

X = 2

We can see that 1<2<3, hence there exists 2 between 1 and 3. And f’(2) = 0.

This means that the Rolle’s theorem holds good for the given function and given interval.

1.2. Mean value theorems

Lagrange’s Mean value Theorem:-

Suppose that f(x) be a function of x such that,

1. If it is continuous in [a , b]

2. If it is differentiable in (a , b)

Then there atleast exists a value cϵ (a , b)

f’(c) =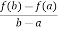

Proof:

Lets define a function g(x),

g(x) = f(x) – Ax  ………………..(1)

Here A is a constant which is to be determined,

So that,  g(a) = g(b)

Now,

g(a) = f(a) – Aa

g(b) = f(b) – Ab

So,

g(a) = g(b),

f(a) – Aa = f(b) – Ab ,

Which gives,

A = 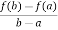    …………………..(2)

As right hand side of eq.(1) is continuous in [a,b] , so that g(x) is continuous.

And right hand side of eq.(1) is differential in (a,b) , so that g(x) is differentiable in (a,b).

And g(a) = g(b) , because of the choice of A.

Hence g(x) satisfies all the conditions of Rolle’s theorem.

So that,

There exists a value c  such that a<c<b at which g’(c) = 0

Now, differentiate eq. (1) with respect to x, we get

g’(x) = f’(x) – A

Here we know that, x = c,

g’(c) = f’(c) – A

As g’(c) = 0, then

f’(c) – A =0

So that,, f’(c) = A,

From equation (2) , we get

f’(c) = 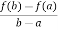                                            hence proved.

Example-1:

Verify the Lagrange’s mean value theorem for

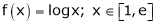
Solution:

Here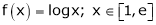

i)      Clearly f(x) = log x is logarithmic function. Hence it is continuous in [1, e]

Ii)    Consider f(x) = log x.

Diff. w.r.t. x we get,

Clearly f’(x) exists for each value of 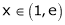& is finite.

Hence all conditions of LMVT are satisfied Hence at least

Such that

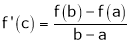
i.e.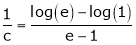

i.e.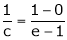

i.e.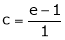

i.e.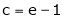

Since e = 2.7183

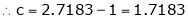
Clearly c = 1.7183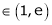

Hence LMVT is verified.

Example-2:

Verify mean value theorem for f(x) = tan-1x in [0, 1]

Solution:

Here ;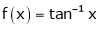

i)      Clearly 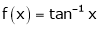is an inverse trigonometric function and hence it is continuous in [0, 1]

Ii)    Consider

Diff. w.r.t. x we get,

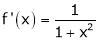
Clearly f’(x) is continuous and differentiable in (0, 1) & is finite

Hence all conditions of LMVT are satisfied, Thus there exist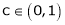

Such that

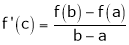
i.e.

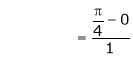
i.e.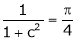

i.e.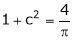

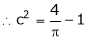
i.e.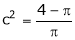

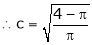
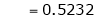
Clearly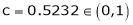

Hence LMVT is verified.

Example-4;

Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].

Sol. As we see that the given function is a polynomial and we know that the polynomial is continuous in [0,4] and differentiable in (0,4).

f(x) = (x-1)(x-2)(x-3)

f(x) =  x-6x²+11x-6

Now at x = 0, we get

f(0) = -6  and

At x = 4, we get.

f(4) = 6

Diff. The function w.r.t.x , we get

f’(x) = 3x²-6x+11

Suppose x = c, we get

f’(c) = 3c²-6c+11

By Lagrange’s mean value theorem,

f’(c) = 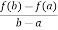    =  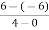   =   = 3                                                                                                                        

Now we get,

3c²-6c+11 = 3

3c²-6c+8 = 0

On solving the quadratic equation, we get

C = 2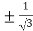   

Here we see that the value of c lies between 0 and 4

Therefore the given function is verified.

Meaning of sign of Derivative:

Let f(x) satisfied LMVT in [a, b]

Let x1 and x2 be any two points laying (a, b) such that x1< x2

Hence by LMVT, such that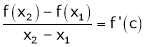

i.e. 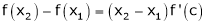      … (1)

Cast I:

If 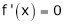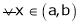then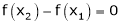

i.e.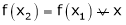

is constant function

Case II:

If 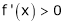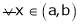then from equation (1)

i.e.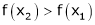

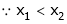Means x2 - x1> 0 and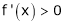

Thus for x2> x1

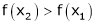
Thus f(x) is increasing function is (a, b)

Case III:

If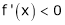

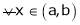
Then from equation (1)

i.e.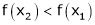  

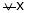
Since and then 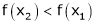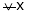hence f(x) is strictly decreasing function.

Example-5:

Prove that

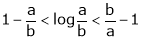
And hence show that

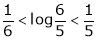
Solution:

Let

; 

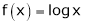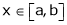
i)      Clearly 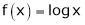is a logarithmic function and hence it is continuous also

Ii)    Consider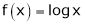

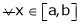
Diff. w.r.t. x we get,

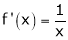
Clearly f’(x) exist and finite in (a, b) Hence f(x) is continuous and differentiable in (a, b). Hence by LMVT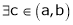

Such that

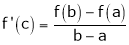
i.e.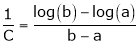

i.e.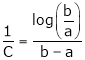

Since

a < c < b

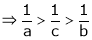
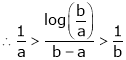
i.e.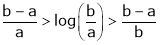

i.e.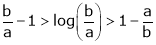

i.e.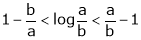

i.e.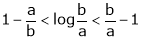

Hence the result

Now put a = 5, b = 6 we get

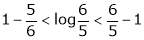
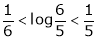
Hence the result

Example-6:

Prove that 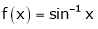, 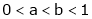use mean value theorem to prove that,

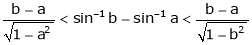
Hence show that

Solution:

i)     Let f(x) = sin-1x; 

Ii)    Clearly f(x) is inverse trigonometric function and hence it is continuous in [a, b]

Iii)  Consider f(x) = sin-1x

Diff. w.r.t. x we get,

Clearly f’(x) is finite and exists for 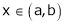. Hence by LMVT, 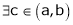such that

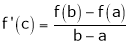
i.e.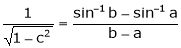

Since a < c < b

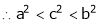
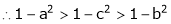
i.e.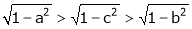

i.e.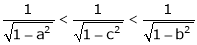

i.e.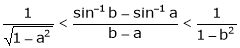

i.e.

Hence the result

Put we get

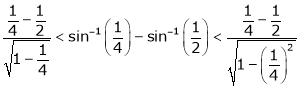
i.e.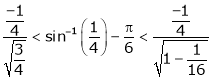

i.e.

i.e.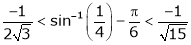

i.e.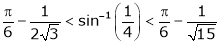

Hence the result

Cauchy’s Mean Value Theorem:

Suppose we have two functions f(x) and g(x) of x, such that,

1. Both functions are continuous in [a,b]

2. Both functions are differentiable in (a,b)

3. g’(x) ≠ 0 for any x ϵ (a,b)

These three exists atleast , x = c ϵ (a,b) , at which

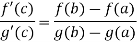
Proof: Suppose, we define a functions,

h(x) = f(x) – A.g(x) …………………….(1)

So that h(a) = h(b) and A is a constant to be determined.

Now,

h(a) = f(a) – Ag(a)

h(b) = f(b) – A.g(b)

So that,

f(a) – Ag(a) = f(b) – A.g(b) , which gives

A = 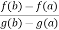    …………………………….(2)

Now, h(x) is continuous in [a,b] as RHS of eq. (1) is continuous in [a,b] and h(x) is diff. In (a,b) as RHS of eq. (1) is diff. In (a,b)

Also,

h(a) = h(b)

Therefore all the conditions of Rolle’s theorem are satistfied then there exists a Value x = cϵ (a,b)

So that h’(c) = 0

Differentiate eq.(1) w.r.t. x , we get

h’(x) = f’(x) – A.g’(x)

At x = c

h’(c) = f’(c) – A.g’(c)

0 = f’(c) – A.g’(c)

A =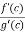

So that, we get

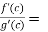
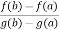    where a<c<b

Hence the Cauchy’s mean value theorem is proved.

Example-7:

Verify Cauchy mean value theorems for 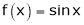&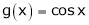in

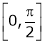
Solution:

Let &;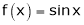

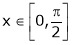
i)      Clearly f(x) and g(x) both are trigonometric functions. Hence continuous in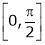

Ii)    Since &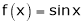

Diff. w.r.t. x we get,

&

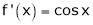Clearly both f’(x) and g’(x) exist & finite in 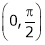. Hence f(x) and g(x) is derivable in 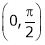and

Iii)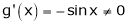   

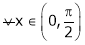
Hence by Cauchy mean value theorem, there exist at least 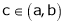such that

i.e.

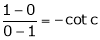
i.e. 1 = cot c

i.e.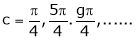

Clearly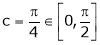

Hence Cauchy mean value theorem is verified.

Example-8:

Considering the functions ex and e-x, show that c is arithmetic mean of a & b.

Solution:

i)      Clearly f(x) and g(x) are exponential functions Hence they are continuous in [a, b].

Ii)    Consider &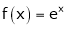

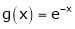
Diff. w.r.t. x we get

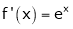and

Clearly f(x) and g(x) are derivable in (a, b)

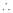By Cauchy’s mean value theorem 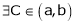such that

i.e.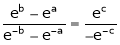

i.e.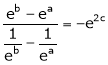

i.e.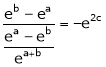

i.e.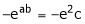

i.e.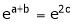

i.e.

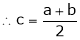
Thus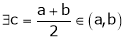

i.e. c is arithmetic mean of a & b.

Hence the result

Example-9

Show that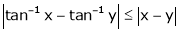

Prove that if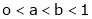

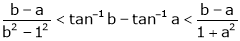and Hence show that

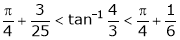
Verify Cauchy’s mean value theorem for the function x2 and x4 in [a, b] where a, b > 0

If for 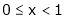then prove that,

[Hint:, ]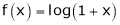

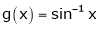Example-10:

Verify Cauchy’s mean value theorem for the function f(x) = x⁴ and g(x) = x² in the interval [1,2]

Sol. We are given, f(x) = x⁴ and g(x) = x

Derivative of these fucntions ,

f’(x) = 4x³ and g’(x) = 2x

Put these values in Cauchy’s formula, we get

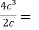
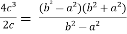
2c² =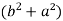

c² =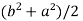

c =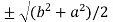

Now put the values of a = 1 and b = 2 ,we get

c = 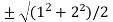= =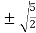 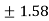(approx..)

Hence the Cauchy’s theorem is verified.

1.3. Taylor’s and Maclaurin’s theorem with remainders

Taylor’s Series Expansion:-

a)     The expansion of f(x+h) in ascending power of x is

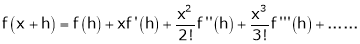
b)    The expansion of f(x+h) in ascending power of h is

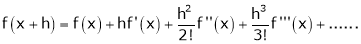
c)     The expansion of f(x) in ascending powers of (x-a) is,

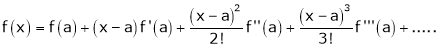
Using the above series expansion we get series expansion of f(x+h) or f(x).

Expansion of functions using standard expansions-

Example-1:

Expand 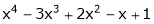in power of (x – 3)

Solution:

Let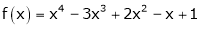

Here a = 3

Now by Taylor’s series expansion,

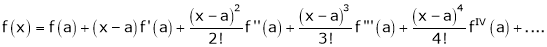 … (1)

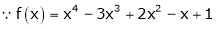
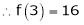
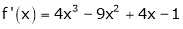
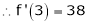
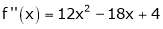
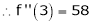
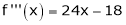
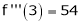
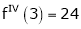
equation (1) becomes.

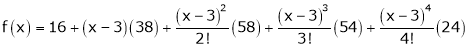
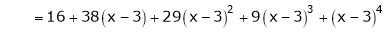
Example-2:

Using Taylors series method expand

in powers of (x + 2)

Solution:

Here

a = -2

By Taylors series,

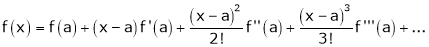   … (1)

Since

,  , …..

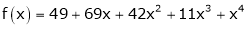
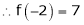
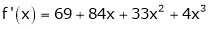
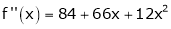
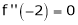
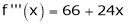
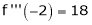
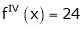
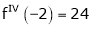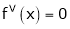Thus equation (1) becomes

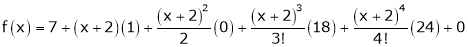
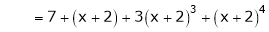
Example-3:

Expand in ascending powers of x.

Solution:

Here

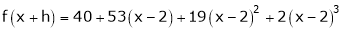
i.e.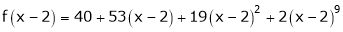

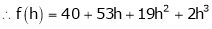
Here h = -2

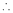By Taylors series,

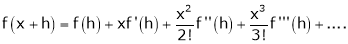    … (1)

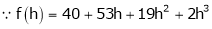
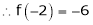
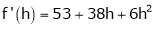
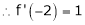
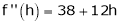
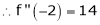
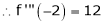
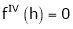
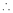equation (1) becomes,

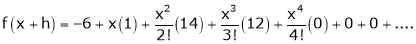
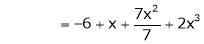
Thus

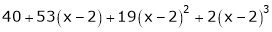
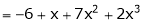
Example-4:

Expand 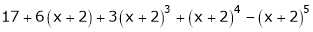in powers of x using Taylor’s theorem,

Solution:

Here

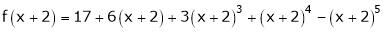
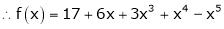
i.e.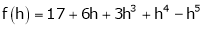

Here

h = 2

By Taylors series

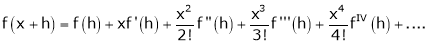  … (1)

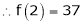
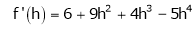
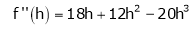
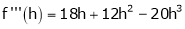
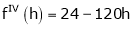
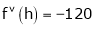
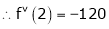
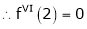
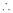By equation (1)

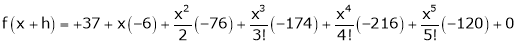
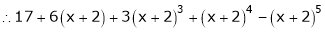
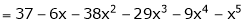
Example-5: Expand the function 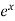in ascending powers of (x – 1) by using Taylor’s theorem.

Sol. We know that the Taylor’s theorem for the function f(x) in ascending powers of (x – a) is,

f(x) = f(a) + (x – a)f’(a) + 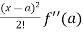 + ……….                ………….(1)

Here f(x) = 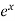and a = 1

Now,

f’(x) = 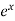and f’(a) = e

f’’(x) = and f’’(a) = e

Put these values in equation (1),

…………….

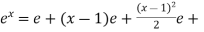Take ‘e’ as common,

…………….}

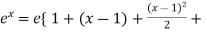Which is the required expansion.

Maclaurin’s theorem-

Maclaurin’s theorem is the special case of Taylor’s  theorem.

Which is stated as below-

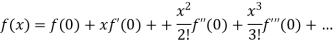
Example: Expand log (1 + x) by using Maclairin’s theorem.

Sol. Here,

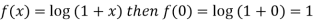
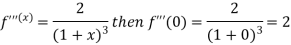
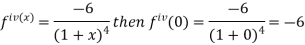
Put these values in Maclaurin’s theorem-

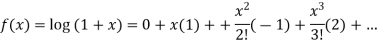
Example: Expand as far as the term in .

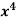Sol.

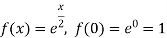
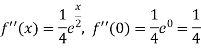
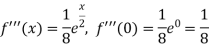
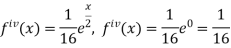
Put these values in Maclaurin’s theorem, we get-

1.4. Indeterminate forms & L’Hospital rule

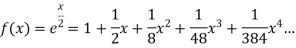
Let we have two functions f(x) and g(x) and-

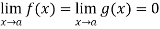
Then-

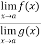is an expression of the form , in that case we can say that f(x)/g(x) is an indeterminate for of the type   at x = a.

Now, Let we have two functions f(x) and g(x) and-

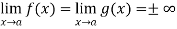
Then-

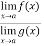is an expression of the form , in that case we can say that f(x)/g(x) is an indeterminate for of the type   at x = a.

Some other indeterminate forms are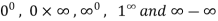

L’Hospital’s rule for form-

Working steps-

1. Check that the limits f(x)/g(x) is an indeterminate form of type .

(note- we can not apply L’Hospital rule if it is not in indeterminate form)

2. Differentiate f and g separately.

3. Find the limits of the derivatives .if the limit is finite , 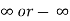then it is equal to the limit of f(x)/g(x).

Example-1: Evaluate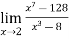

Sol. Here we notice that it is an indeterminate form of .

So that , we can apply L’Hospital rule-

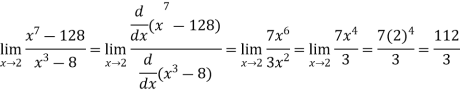
Example-2: Evaluate .

Sol. Let f(x) = 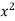and g(x) = .

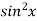Here we see that this is the indeterminate form of 0/0 at x = 0.

Now by using L’Hospital rule, we get-

=

=

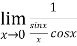
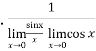= = 1

Note- Suppose we get an indeterminate form even after finding first derivative, then in that case , we use the other form of L’Hospital’s rule.

If we have f(x) and g(x) are two functions such that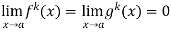 

.

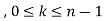If 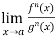exist or (∞ , -∞), then

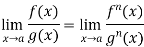
Example-3: Evaluate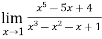

Sol. Let f(x) = 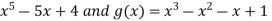, then

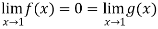
And

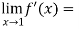
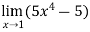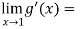
= 0

= 0

But if we use L’Hospital rule again, then we get-

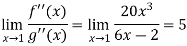
Example-4: Evaluate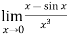

Sol. We can see that this is an indeterminate form of type 0/0.

Apply L’Hospital’s rule, we get

But this is again an indeterminate form, so that we will again apply L’Hospital’s rule-

We get

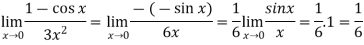
L’Hospital’s rule for form-

Let f and g are two differentiable functions on an open interval containing x = a, except possibly at x = a and that

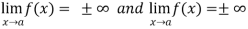
If 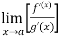has a finite limit, or if it is 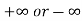, then

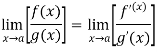
Theorem- If we have f(x) and g(x) are two functions such that  .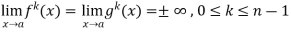

If 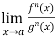exist or (∞ , -∞), then

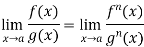
Example-5: Find 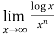  , n>0.

Sol. Let f(x) = log x and g(x) =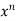

These two functions satisfied the theorem that we have discussed above-

So that,

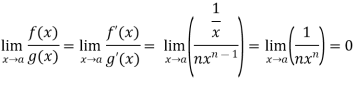
Example-6: Evaluate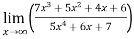

Sol. Apply L’Hospital rule as we can see that this is the form of

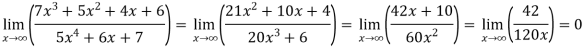
Example-7:

Note- In some cases like above example, we can not apply L’Hospital’s rule.

Other types of indeterminate forms-

Example-8: Evaluate

Sol. Here we find that-

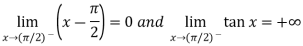
So that this limit is the form of 0.

Now,

Change 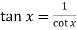to obtain the limit-

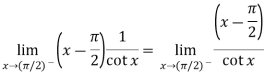
Now this is the form of 0/0,

Apply L’Hospital’s rule-

1.5. Maxima and minima

If  f(x) is a single valued function defined in a region R then

Maxima is a maximum point if and only if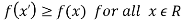

Minima is a minimum point 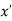if and only if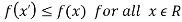   

Maxima and Minima of a function of two independent variables

Let 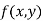be a defined function of two independent variables.

Then the point 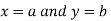is said to be a maximum point of if

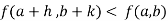
Or   =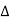

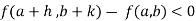
For all positive and negative values of h and k.

Similarly the point 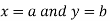is said to be a minimum point o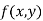f if

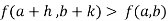
Or   =

For all positive and negative values of h and k.

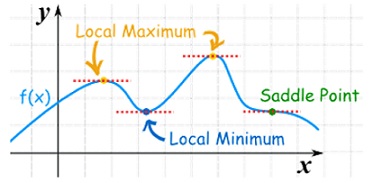
Saddle point:Critical points of a function of two variables are those points at which both partial derivatives of the function are zero. A critical point of a function of a single variable is either a local maximum, a local minimum, or neither. With functions of two variables there is a fourth possibility - a saddle point.

A point is a saddle point of a function of two variables if

At the point.

Stationary Value

The value 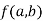is said to be a stationary value o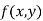f if

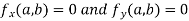
i.e. the function is a stationary at (a , b).

Rule to find the maximum and minimum values of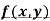

1. Calculate.
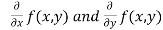2. Form and solve 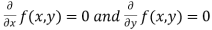, we get the value of x and y let it be pairs of values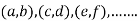
3. Calculate the following values :

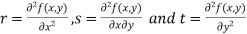
4.     (a) If

(b) If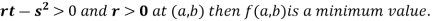

(c) If

(d) If

Example1 Find out the maxima and minima of the function

Given 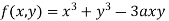    …(i)

Partially differentiating (i) with respect to x we get

    ….(ii)

Partially differentiating (i) with respect to y we get

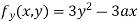    ….(iii)

Now, form the equations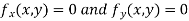

Using (ii) and (iii) we get

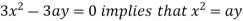
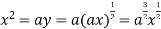          using above two equations

Squaring both side we get

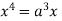
Or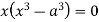 

This show that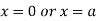

Also we get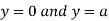

Thus we get the pair of value as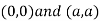

Now, we calculate

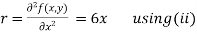
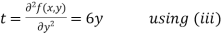
Putting above values in

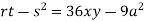
At point (0,0)  we get

So, the point (0,0) is a saddle point.

At point 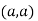we get

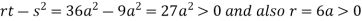
So the point 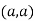is the minimum point where

In case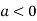 

So the point 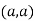is the maximum point where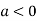

Example2 Find the maximum and minimum point of the function

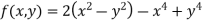
Partially differentiating given equation with respect to and x and y then equate them to zero                 

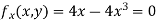
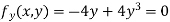
On solving above we get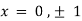 

Also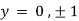

Thus we get the pair of values (0,0), (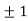,0) and (0,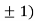

Now, we calculate

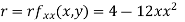
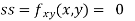
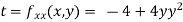
At the point (0,0)

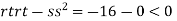
So function has saddle point at (0,0).

At the point (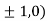

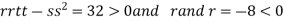
So the function has maxima at this point (.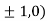

At the point (0,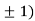

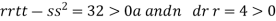
So the function has minima at this point (0,.

At the point (

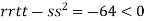
So the function has an saddle point at (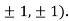

Example3 Find the maximum and minimum value of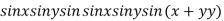

Let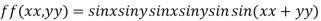

Partially differentiating given function with respect to x and y and equate it to zero

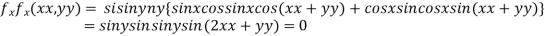  ..(i)

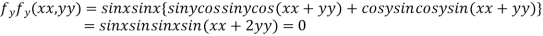    ..(ii)

On solving (i) and (ii) we get

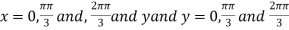
Thus pair of values are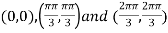

Now, we calculate

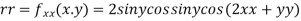
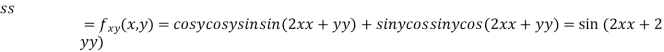
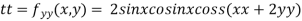
At the point (0,0)

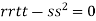
So further investigation is required

On the x  axis y  = 0  , f(x,0)=0

On the line y=x,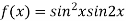

At the point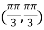

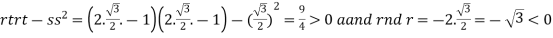
So that the given function has maximum value at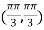

Therefore maximum value of given function

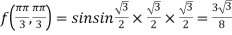
At the point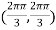

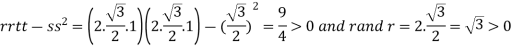
So that the given function has minimum value at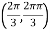

Therefore minimum value of the given function

1.6. Evaluation of definite and improper integrals

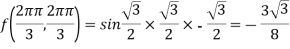
When we apply limits in indefinite integrals are called definite integrals.

If an expression is written as 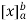, here ‘b’ is called upper limit and ‘a’ is called lower limit.

If f is an increasing or decreasing function on interval [a , b], then

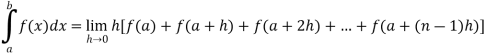
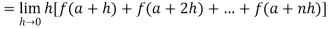
Where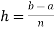 

Properties-

1. The definite integral applies only if a<b, but it would be appropriate to include the case a = b and a>b as well, in that case-

If a = b, then

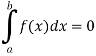
And if a>b, then

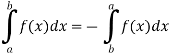
2. Integral of a constant function-

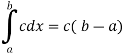
3. Constant multiple property-

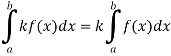
4. Interval union property-

If a < c < b, then

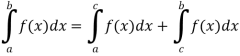
5. Inequality-

If c and d are constants such that 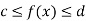for all x in [a , b], then

c(b – a)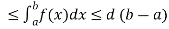

Note- if a function f:[a , b]→R is continuous, then the function ‘f’ is always Integrable.

Example-1: Evaluate.

Sol. Here we notice that  f:x→cos x  is a decreasing function on [a , b],

Therefore by the definition of the definite integrals-

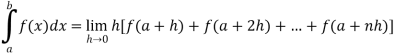
Then

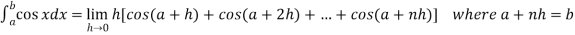
Now,

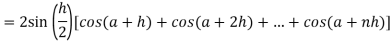
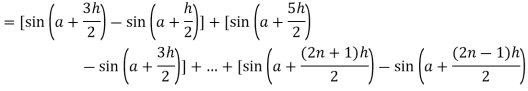
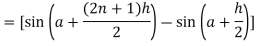
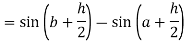
Here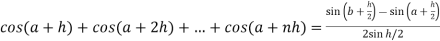

Thus

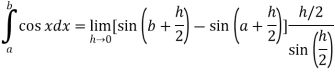
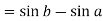
Example-2: Evaluate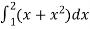

Sol. Here 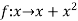is an increasing function on [1 , 2]

So that,

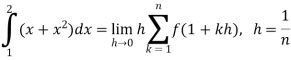
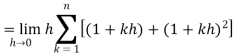
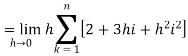
  …. (1)

We know that-

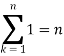
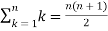
And

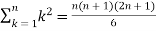
Then equation (1) becomes-

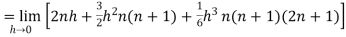
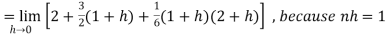
Note- we can find the definite integral directly as-

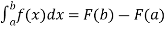
Example-3:  Evaluate-                                          

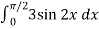
Sol.         

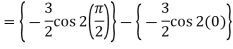
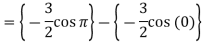
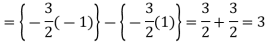
Improper integrals

(1) Let f is function defined on [a , ∞) and it is integrable on [a , t] for all t >a, then

If 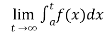exists, then we define the improper integral of f over [a , ∞) as follows-

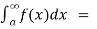
(2) Let f is function defined on (-∞,b] and it is integrable on [t , b] for all t >b, then

If 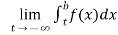exists , then we define the improper integral of f over (-∞ , b] as follows-

(3) ) Let f is function defined on (-∞, ∞] and it is integrable on [a , b] for every closed and bounded interval [a , b] which is the subset of R., then

If 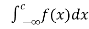and 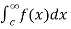exist for some c belongs to R , then we define the improper integral of f over (-∞ , ∞ ) as follows-

+

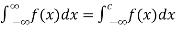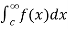
(4) Let f is function defined on (a , ∞) and 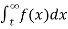exists for all t>a , then

If 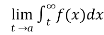exists , then we define the improper integral of f over (a , ∞) as follows-

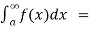
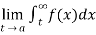
(5)  ) Let f is function defined on (-∞ , b) and 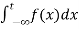exists for all t<b  , then

If 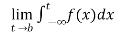exists , then we define the improper integral of f over (-∞ , b) as follows-

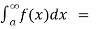
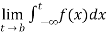
Improper integrals over finite intervals-

(1) Let f is function defined on (a, b] and 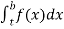exists for all t ∈(a,b)  , then

If 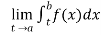exists , then we define the improper integral of f over (a , b] as follows-

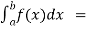
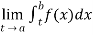
(2) Let f is function defined on [a, b) and 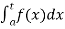exists for all t ∈(a,b)  , then

If 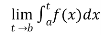exists , then we define the improper integral of f over [a , b) as follows-

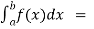
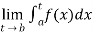
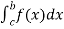(3) Let f is function defined on [a, c) and (c , b] . If and   exist

Then we define the improper integral of f over [a , b] as follows-

1.7. Application of definite integrals to evaluate surface areas and volumes of revolutions

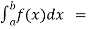
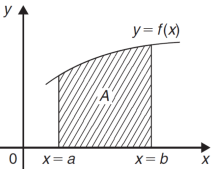
Area under and between the curves-

Total shaded area will be as follows of the given figure( by using definite integrals)-

Total shaded area =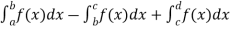

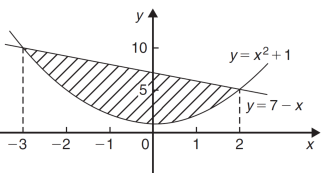
Example-1: Determine the area enclosed by the curves-

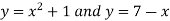
Sol. We know that the curves are equal at the points of interaction, thus equating the values of y of each curve-

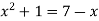
Which gives-

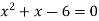
By factorization,

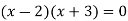
Which means,

x = 2 and x = -3

By determining the intersection points the range the values of x has been found-

x	-3	-2	-1	0	1	2
1	10	5	2	1	2	5

And

We get the following figure by using above two tables-

Area of shaded region =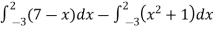

=

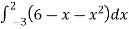
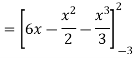
= ( 12 – 2 –  8/3 ) – (-18 – 9/2 + 9)

=

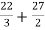
= 125/6 square unit

Example-2: Determine the area bounded by three straight lines y = 4 – x, y = 3x and 3y = x

Sol. We get the following figure by using the equations of three straight lines-

y = 4 – x, y = 3x and 3y = x

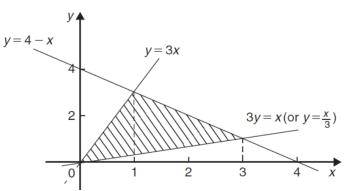
Area of shaded region-

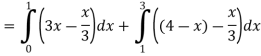
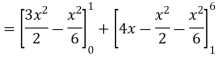
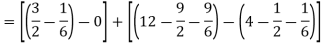
Example-3: Find the area enclosed by the two functions-

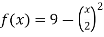and g(x) = 6 – x

Sol. We get the following figure by using these two equations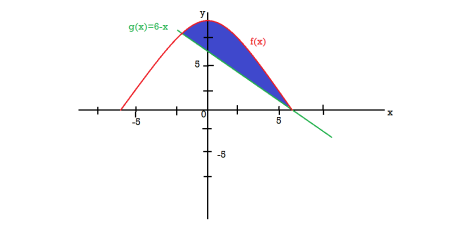                                 

To find the intersection points of two functions f(x) and g(x)-

f(x) = g(x)

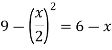
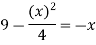
On factorizing, we get-

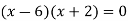
x = 6, -2

Now

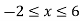
Then, area under the curve-

A =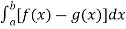

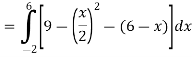
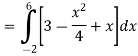
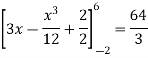
Therefore the area under the curve is 64/3  square unit.

Areas and volumes of revolutions

The volume of revolution (V) is obtained by rotating area A through one revolution about the x-axis is given by-

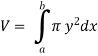
Suppose the curve x = f(y) is rotated about y-axis between the limits y = c and y = d, then the volume generated V, is given by-

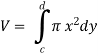
Example-1:  Find the area enclosed by the curves 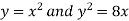and if the area is rotated about the x-axis then determine the volume of the solid of revolution.

Sol. We know that, at the point of intersection the coordinates of the curve are equal. So that first we will find the point of intersection-

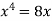
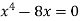
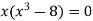
We get,

x = 0 and x = 2

The curve of the given equations will look like as follows-

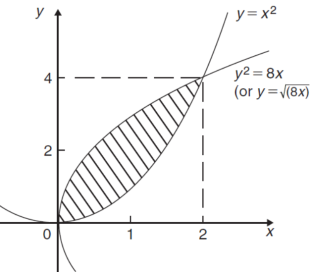
Then,

The area of the shaded region will be-

A =

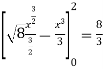
So that the area will be 8/3 square unit.

The volume will be

= (volume produced by revolving 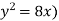– (volume produced by revolving

=

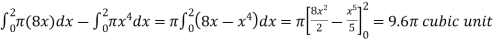
Method of cylindrical shells-

Let f(x) be a continuous and positive function. Define R as the region bounded above by the graph f(x), below by the x-axis, on the left by the line x = a and on the right x = b, then the volume of the solid of revolution formed by revolving R around the y-axis is given by

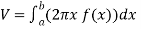
Example-2: Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 1/x over the interval [1 , 3].

Sol. The graph of the function f(x) = 1/x will look like-

The volume of the solid of revolution generated by revolving R(violet region) about the y-axis over the interval [1 , 3]

Then the volume of the solid will be-

Example-3: Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 2x - x² over the interval [0 , 2].

Sol. The graph of the function f(x) = 2x - x² will be-

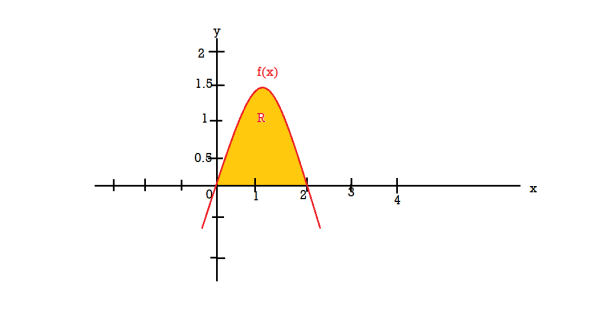
The volume of the solid is given by-

=
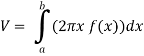
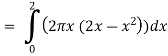
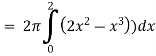