Unit 3
Thermodynamics
- Nernst Equation
Any change in the Gibbs free energy G directly correspond to changes in free energy for processes at constant temperature and pressure, change is the maximum non-expansion work obtainable under these conditions in a closed system; ΔG is negative for spontaneous process, positive for nonspontaneous process, and zero for processes at equilibrium.
It takes into consideration the values of the standard electrode potentials, temperature, activity and the reaction quotient for the calculation of cell potential. For any cell reaction, that occurs Gibbs free energy can be related to standard electrode potential as:
ΔG =-nFE
Where, n = number of electrons transferred in the reaction, ΔG= Gibbs free energy, E= cell potential F = Faradays constant (96,500 C/mol) and. Under standard conditions, the above equation can be written as,
ΔGo =-nFEo
According to the theory of thermodynamics, Gibbs free energy under general conditions can be related to Gibbs free energy under standard condition and the reaction quotient as:
ΔG=ΔGo + RT lnQ
Where, Q= reaction quotient, R= universal gas constant and T= temperature in Kelvin. Incorporating the value of ΔGo and ΔG, from the first two equations, we get the equation:
-nFE = -nFE0 + RT lnQ
E = E0 – (RT/nF) lnQ
By conversion of Natural log to log10, the above equation is called as the Nernst equation. Here, it shows the relation of the reaction quotient and the cell potential. Special cases of Nernst equation:
E = Eo − (2.303RT/nF) log10Q
At standard temperature, T= 298K:
E = Eo − (0.0592V/n) log10Q
At standard temperature T = 298 K, the 2.303RTF, term equals 0.0592 V.
Under Equilibrium Condition
As the redox reaction in the cell progresses, the concentration of reactants decreases while the concentration of products increases. This process goes on until equilibrium is achieved. At equilibrium, ΔG = 0. Hence, cell potential, E = 0. Thus, the Nernst equation can be modified to:
E0 – (2.303RT/nF) log10Keq = 0
E0 = (2.303RT/nF) log10Keq
Where, Keq = equilibrium constant and F= faradays constant. Therefore, the above equation gives us a relation between standard electrode potential of the cell where the reaction takes place and the equilibrium constant.
Applications of Nernst Equation
One of the major applications of Nernst equation is in determining ion concentration
- It is also used to calculate the potential of an ion of charge “z” across a membrane. It is used in oxygen and the aquatic environment.
- It is also used in solubility products and potential-metric titrations.
- It is also used in pH measurements and to determine the Concentration Cell is an electrochemical cell.
The branch which deals with the movement of energy from one form to the other and the relationship that exists between heat and temperature with energy and the work done is called as thermodynamics. Thermodynamics is a branch of Science that deals with the different forms of energy and work done in a system. Thermodynamics is only confined to Large scale response of a system which we are observed and measured in experiments
Energy:
It referred to the energy content that is present within the system. The energy represents the overall energy contained in the system and may include many forms of energy such as potential energy, kinetic energy etc. In a chemical reaction, we know the energy transformations and basic thermodynamics gives us information regarding energy change associated with the particles present in a system.
Factors affecting the internal energy
The internal energy of a system may change when:
- Heat passes into or out of the system,
- Work is done on or by the system or matter enters or leaves the system
Work:
Work done by a system is defined as the amount of energy exchanged between a system and its surroundings. Work is completely determined by external factors such as an external force, pressure or volume or change in temperature etc.
Heat:
Heat in thermodynamics is defined as the kinetic energy of the molecules of the substance or material. Heat and thermodynamics together form the basics which help process designers and engineers to optimize their processes and harness the energy associated with chemical reactions economically.
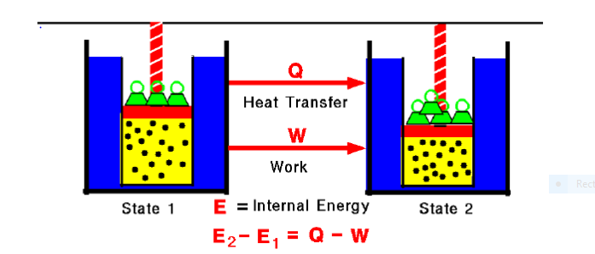
Fig. 1:
Any thermodynamic system in an equilibrium state possesses a state variable called the internal energy (E). Between any two equilibrium states, the change in internal energy is equal to the difference of the heat transfer into the system and work done by the system.
- Enthalpy:
Enthalpy a process or activity takes place at constant pressure, the heat released or absorbed is equal to the Enthalpy change. Enthalpy is occasionally called or known as “heat content”, “enthalpy” is derived from the Greek word which means “warming”. Enthalpy(H) is the sum of the internal energy(U) and the result of pressure(P) and volume(V).
Enthalpy H is written as,
H = U + PVm
Where, H = is the Enthalpy of the system
U = is the Internal energy of the system and is entirely dependent on the state functions T, p and U.
Enthalpy can also be written as
ΔH=ΔU+ΔPV.
P = is the Pressure of the system
V = Volume of the system Enthalpy is not directly measured, but the change in enthalpy (ΔH) is measured, which is the heat lost or added by the system,
Entropy:
It was Introduced by the German Physicist Rudolf Clausius in 1850, and is a highlight of 19th century Physics. The word “entropy” is derived from the Greek word, which means “turning”. It was derived to provide a quantitative measure for the spontaneous changes and Clausius introduced the concept of entropy as a precise way of expressing the Second Law of Thermodynamics, Clausius form of the second law states that spontaneous change for an irreversible process in an isolated system is a measure of randomness or irregularity or disorder of the system?
The more or the randomness, higher is the entropy.
Solid state has the lowest or least entropy, the gaseous state has the highest entropy and the liquid state has the entropy that lies between the two.
Entropy is a state function. The changes in its value during any process, is called the entropy change.
ΔS = S2 -S1 = ∑S products – ∑S reactants
1) When a system absorbs heat, the molecules begin to move faster because the kinetic energy increases. Therefore, disorder increases. Greater the heat absorbed, greater will be the disorder.
2) For equal amount of heat absorbed at low temperature, the disorder will be more than at high temperature. This proves that entropy change is inversely proportional to temperature.
ΔS = eve / T
Entropy change during a process is defined as the quantity of heat (q) absorbed isothermally and reversibly divided by the absolute Temperature (T) at which the heat is absorbed.
- Free Energy
Gibbs Free Energy is a measure of the potential for reversible or maximum work that may be done by a system at constant temperature and pressure. It is a thermodynamic function that was discovered in 1876 by Josiah Willard Gibbs to assume if a process will occur spontaneously at constant temperature and pressure. Gibbs free energy G is defined as
G = H - TS
Where H, T, and S are the Enthalpy, temperature, and entropy. The SI unit for Gibbs energy is the kilojoule.
Equations to interrelate thermodynamic properties
Gibbs free energy combines both the enthalpy and entropy into a single value.
Gibbs free energy is the energy t with a that associates itself with a chemical reaction. It equals the enthalpy minus the temperature of the product and the entropy of the system.
G=H-TS
At constant temperature
ΔG = ΔH – TΔS
ΔG predicts the direction of a chemical reaction. If ΔG value is negative, then the corresponding reaction is spontaneous. If ΔG value is positive then reaction is non-spontaneous.
ΔGº=ΔHº-TΔSº
Where
ΔGº = Gibbs free energy (J or KJ)
ΔHº=enthalpy
T=Temperature
ΔSº=Entropy
Gibbs free energy is the energy that is available to do quality work.
A reaction will spontaneously occur if ΔG<0 (exergonic reaction)
A reaction will not spontaneously occur if ΔG>0 (endergonic reaction).
If ΔG value is less than zero, there is a thermodynamic force for the reaction or it drives the process in the forward direction.
When ΔG is positive, then reactants are favored, when ΔG=0 system is at equilibrium.
- EMF
Electromotive force, or, as it is often written, e.m.f., is described as that source of energy which enables electrons movement around an electric circuit.
For any object to move from rest, there has to be some energy change. To ensure electrons movement round an electrical circuit, they should receive energy from a source of e.m.f. Which usually is a battery or a generator.
For every coulomb of electricity to move completely around an electrical circuit, a certain amount of electrical energy is needed, which depends on the particular circuit. The e.m.f. Is expressed in volts and is numerically the number of joules of energy given by the source of e.m.f. To each coulomb to enable movement around the circuit. The symbol for volt is the capital letter V.
Thus
Joules coulombs=volts.
It follows that:
Joules=volts × coulombs = volts × ampers × seconds.
A 12-volt (12-V) battery is able to give 12 joules (12 J) of energy to each coulomb to enable movement around an electrical circuit.
The symbol for e.m.f. Is the capital letter E.
Example:
Calculate the energy supplied by a 12v battery when a current of 4 A flows for 10 minutes.
Energy supplied = Volts x amperes x seconds
= 12 x 4 x (10 x 60) Joules
= 28,800 J
- Cell Potential
(1) “The difference in potentials of the two half – cells of a cell known as electromotive force (emf) of the cell or cell potential.”
The potential difference of the two half – cells of a cell arises because of the flow of electrons from anode to cathode and flow of current from cathode to anode.
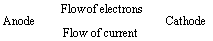
(2) The emf of the cell or cell potential can be calculated from the values of electrode potentials of two half – cells constituting the cell. The following three methods are in use
(i) When oxidation potential of anode and reduction potential of cathode are taken into consideration
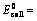Oxidation potential of anode + Reduction potential of cathode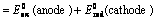 
(ii) When reduction potentials of both electrodes are taken into consideration
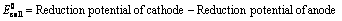
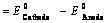
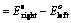
(iii) When oxidation potentials of both electrodes are taken into consideration
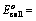Oxidation potential of anode – Oxidation potential of cathode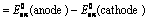 
Lead storage battery is the most common device used to store energy in the portable form. This is also called as lead acid battery. Although the batteries are reliable, which contain acidic material inside that required a proper disposal method after its complete use. These batteries have moderate power density and good time. The battery consists of lead grids on its electrodes. The anodic grid opening is filled with spongy lead while the cathodic grid consists of lead oxide (PbO2).
Charge Chemistry of the battery:
Charge batteries are those batteries which can be recharged after single use. In this type of battery each plate contains negative as well as the positive end. The negative plate is of lead while the positive plate is made up of lead oxide in an electrolyte of approx 4.0M sulphuric acid.
Negative plate reaction:
PbSO4(s) + H+(aq) + 2e– → Pb(s) + HSO4–(aq)
Positive plate reaction:
PbSO4(s) + 2H2O(l) → PbO2(s) + HSO4–(aq) + 3H+(aq) + 2e–
Combining these two reactions, the overall reaction is the reverse of the discharge reaction:
2PbSO4(s) + 2H2O(l) → Pb(s) + PbO2(s) + 2H+(aq) + 2HSO4–(aq)
Discharge Chemistry of the Battery:
The positive and negative plate of the batteries becomes lead sulphate. Due to the loss of sulfuric acid from electrolytes it becomes the water.
Negative plate reaction:
Pb(s) + HSO4–(aq) → PbSO4(s) + H+(aq) + 2e–
Positive plate reaction:
PbO2(s) + HSO4–(aq) + 3H+(aq) + 2e– → PbSO4(s) + 2H2O(l)
Combining these two reactions, one can determine the overall reaction:
Pb(s) + PbO2(s) + 2H+(aq) + 2HSO4–(aq) → 2PbSO4(s) + 2H2O(l)
Corrosion is the disintegration of a metal due to the chemical reactions between the metal and the surrounding environment. Both the types of metal and the environmental conditions, particularly gasses that come in contact with the metal, determine the form and rate of the metal.
All metals can corrode. Some metals, like pure iron, deteriorate very fast. Stainless steel, and, metals that combines with iron and other alloys, is slower to corrode and is therefore used more efficiently.
All small group of metals, are called the Noble Metals, and show much less reaction than others. As a result, they deteriorate rarely. They are, in fact, the only metals that are found in nature in their purest form. The Noble Metals, not unexpectedly, are often very valuable. They include gold, rhodium, silver, palladium, and platinum.
Types of Corrosion
There are different reasons for metal corrosion. Some can be prevented from corrosion by adding alloys to a pure metal. Others can be avoided by carefully combining metals or management of the metal's environment. Some of the most common types of corrosion are described below.
- General Attack Corrosion: This particular corrosion is very common form of corrosion attacks the entire surface of a metal structure. It is caused by chemical or electrochemical reactions.
- Localized Corrosion: This corrosion attacks only a part of a metal structure. There are three types of localized corrosion:
- Pitting -- it involves the creation of small holes in the surface of a metal.
- Crevice corrosion – it is the corrosion that occurs in stagnant locations such as those found under gaskets.
- Filiform corrosion –they are the corrosions that occurs when water gets under a coating such as paint.
- Galvanic Corrosion: This corrosion occurs when two different metals are placed together in a liquid electrolyte such as salt water. In essence, one metal's molecules are drawn towards the other metal, resulting in the corrosion only one of the two metals.
- Environmental Cracking: When environmental conditions are stressful enough, some metal can begin to crack, weaken, or become brittle and fatigue.
Corrosion Prevention
An effective prevention system begins in the design stage with a proper understanding of the environmental conditions and metal properties. Engineers who work with metallurgical experts should select the proper metal or alloy for every situation. They should also be aware of possible chemical interactions between metals used for surfaces, fittings, and fastenings.
The homogenous and physical part of the system is bounded by any surface which is mechanically separable is termed as phase. The phase may be the in the gaseous form, solid form or liquid form. The boundary present between the two interfaces is called as the interface. Air constitutes a single phase only as it contains a mixture of nitrogen, oxygen, carbon dioxide, water vapour etc. A system consisting of only one phase is said to be homogeneous. A mixture of two immiscible liquids such as water and benzene, will exist in two distinct liquid phases and in addition there will be a vapor phase. Thus there will be three phases each separated from the other by a well-defined bounding surface while the system consist of more than one phase is called as the heterogenous phase.
Phase Rule: If the equilibrium between any number of phases is not influenced by gravity, or electrical by surface action but are influenced only by temperature, pressure and concentration , then the number of degrees of freedom (F) of the system is related to the number of components (C ) and number of phases (P) by the following phase rule equation:
F=C-P+2
Liquid Phase:
(i) Liquid phase is depend on the number of liquids present and their miscibility.
(ii) 2 miscible liquids form 2 separate liquid phase.
(iii) 2 miscible liquids form 1 liquid phase only.
Solid Phase:
Each solid forms a separate phase while number of solid phase depends on the number of solids present in it.
Gaseous Phase:
Due to the thoroughly miscible proportions of gases they form phases only.
Eg.: N2 and H2 mixture form phases only.
Applications to water system:
In water there is only one component i.e., water and its phases: ice, water, steam that is solid, liquid and gaseous form. 
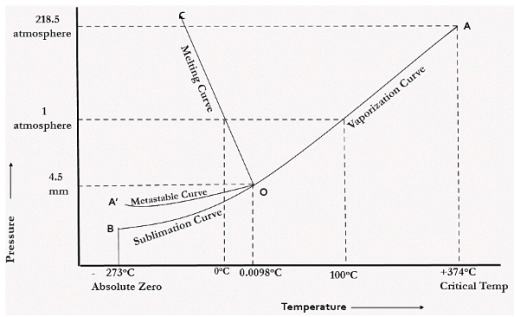
In the figure given above, the horizontal movement leads to be responsible for temperature change while the vertical curve responsible for the pressure change. In the above figure there are three curves i.e., OA,OB,OC which represents the equilibrium conditions between two phases solid with vapour, vapour with liquid and liquid with solid phase of water. Curve OC represents the equilibrium between solid and liquid phase of water. The curve is known as the fusion pressure or melting point curve. Along this curve there are two phases in equilibrium that is ice and water. At atmospheric pressure ice and water can be in equilibrium only at one temperature i.e, the freezing point of the water.
Here, C=1,
P=2
F=C-P+2
=1
Curve OB represent the equilibrium between liquid and vapor. This is called as the vaporization curve. Here also it is necessary to state either temperature or pressure. Eg.: at atmospheric pressure water and vapor can exists in equilibrium only at 1 temperature i.e., the boiling point of the water. Water vapor has also one degree of freedom.
F=C-P+2
=1
