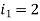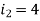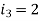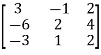UNIT 1
Matrix
Matrices has wide range of applications in various disciplines such as chemistry, Biology, Engineering, Statistics, economics, etc.
Matrices play an important role in computer science also.
Matrices are widely used to solving the system of linear equations, system of linear differential equations and non-linear differential equations.
First time the matrices were introduced by Cayley in 1860.
Definition-
A matrix is a rectangular arrangement of the numbers.
These numbers inside the matrix are known as elements of the matrix.
A matrix ‘A’ is expressed as-

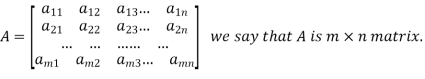
The vertical elements are called columns and the horizontal elements are rows of the matrix.
The order of matrix A is m by n or (m× n)
Notation of a matrix-
A matrix ‘A’ is denoted as-
A = 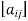
Where, i = 1, 2, …….,m and j = 1,2,3,…….n
Here ‘i’ denotes row and ‘j’ denotes column.
Types of matrices-
1. Rectangular matrix-
A matrix in which the number of rows is not equal to the number of columns, are called rectangular matrix.
Example:
A = 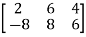
The order of matrix A is 2× 3 , that means it has two rows and three columns.
Matrix A is a rectangular matrix.
2. Square matrix-
A matrix which has equal number of rows and columns, is called square matrix.
Example:
A = 
The order of matrix A is 3 × 3 , that means it has three rows and three columns.
Matrix A is a square matrix.
3. Row matrix-
A matrix with a single row and any number of columns is called row matrix.
Example:
A = 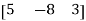
4. Column matrix-
A matrix with a single column and any number of rows is called row matrix.
Example:
A = 
5. Null matrix (Zero matrix)-
A matrix in which each element is zero, then it is called null matrix or zero matrix and denoted by O
Example:
A = 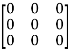
6. Diagonal matrix-
A matrix is said to be diagonal matrix if all the elements except principal diagonal are zero
The diagonal matrix always follows- 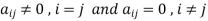
Example:
A = 
7. Scalar matrix-
A diagonal matrix in which all the diagonal elements are equal to a scalar, is called scalar matrix.
Example-
A = 
8. Identity matrix-
A diagonal matrix is said to be an identity matrix if its each element of diagonal is unity or 1.
It is denoted by – ‘I’
I = 
9. Triangular matrix-
If every element above or below the leading diagonal of a square matrix is zero, then the matrix is known as a triangular matrix.
There are two types of triangular matrices-
(a) Lower triangular matrix-
If all the elements below the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.
Example:
A = 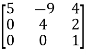
(b) Upper triangular matrix-
If all the elements above the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.
Example-
A = 
Algebra on Matrices:
- Addition and subtraction of matrices:
Addition and subtraction of matrices is possible if and only if they are of same order.
We add or subtract the corresponding elements of the matrices.
Example: 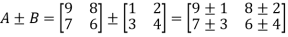
2. Scalar multiplication of matrix:
In this we multiply the scalar or constant with each element of the matrix.
Example: 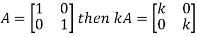
3. Multiplication of matrices: Two matrices can be multiplied only if they are conformal i.e. the number of column of first matrix is equal to the number rows of the second matrix.
Example: 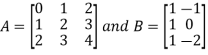
Then 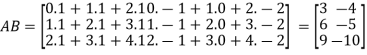
4. Power of Matrices: If A is A square matrix then
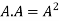
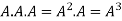 and so on.
and so on.
If 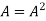 where A is square matrix then it is said to be idempotent.
where A is square matrix then it is said to be idempotent.
5. Transpose of a matrix: The matrix obtained from any given matrix A , by interchanging rows and columns is called the transpose of A and is denoted by 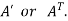
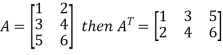
The transpose of matrix 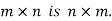 Also
Also 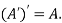
Note: 
6. Trace of a matrix-
Suppose A be a square matrix, then the sum of its diagonal elements is known as trace of the matrix.
Example- If we have a matrix A-
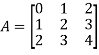
Then the trace of A = 0 + 2 + 4 = 6
Symmetric matrix-
Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.
For example:
 and
and 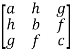
Example: check whether the following matrix A is symmetric or not?
A = 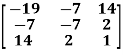
Sol. As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.
So that, first we will find its transpose,
Transpose of matrix A ,
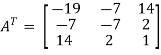
Here,
A = 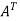
So that, the matrix A is symmetric.
Example: Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.
Sol. Suppose A is any square matrix .
Then,
A = 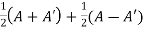
Now,
(A + A’)’ = A’ + A
A+A’ is a symmetric matrix.
Also,
(A - A’)’ = A’ – A
Here A’ – A is an anti – symmetric matrix
So that,
Square matrix = symmetric matrix + anti-symmetric matrix
Hermitian matrix:
A square matrix A = 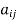 is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
is said to be hermitian matrix if every element of A is equal to conjugate complex j-ith element of A.
It means,
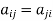
For example:
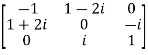
Necessary and sufficient condition for a matrix A to be hermitian –
A = (͞A)’
Skew-Hermitian matrix-
A square matrix A = 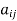 is said to be hermitian matrix if every element of A is equal to negative conjugate complex j-ith element of A.
is said to be hermitian matrix if every element of A is equal to negative conjugate complex j-ith element of A.
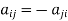
Note- all the diagonal elements of a skew hermitian matrix are either zero or pure imaginary.
For example:
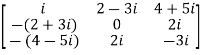
The necessary and sufficient condition for a matrix A to be skew hermitian will be as follows-
- A = (͞A)’
Note: A Hermitian matrix is a generalization of a real symmetric matrix and also every real symmetric matrix is Hermitian.
Similarly a Skew- Hermitian matrix is a generalization of a Skew symmetric matrix and also every Skew- symmetric matrix is Skew –Hermitian.
Theorem: Every square complex matrix can be uniquely expressed as sum hermitian and skew-hermitian matrix.
Or If A is given square complex matrix then 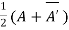 is hermitian and
is hermitian and 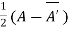 is skew-hermitian matrices.
is skew-hermitian matrices.
Example1: Express the matrix A as sum of hermitian and skew-hermitian matrix where 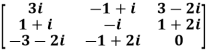
Let A =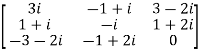
Therefore 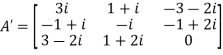 and
and 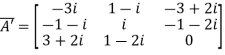
Let 
Again 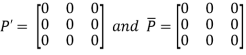
Hence P is a hermitian matrix.
Let 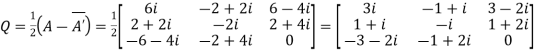
Again 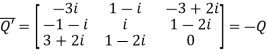
Hence Q is a skew- hermitian matrix.
We Check
P +Q=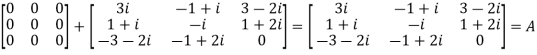
Hence proved.
Example2: If A = 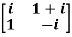 then show that
then show that
(i) 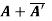 is hermitian matrix.
is hermitian matrix.
(ii) 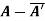 is skew-hermitian matrix.
is skew-hermitian matrix.
Sol.
Given A = 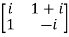
Then 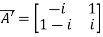
Let 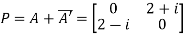
Also 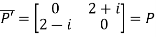
Hence P is a Hermitian matrix.
Let 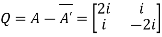
Also 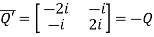
Hence Q is a skew-hermitian matrix.
Skew-symmetric matrix-
A square matrix A is said to be skew symmetrix matrix if –
1. A’ = -A, [ A’ is the transpose of A]
2.all the main diagonal elements will always be zero.
For example-
A = 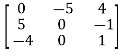
This is skew symmetric matrix, because transpose of matrix A is equals to negative A.
Example: check whether the following matrix A is symmetric or not?
A = 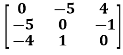
Sol. This is not a skew symmetric matrix, because the transpose of matrix A is not equals to -A.
-A = A’
Orthogonal matrix-
Any square matrix A is said to be an orthogonal matrix if the product of the matrix A and its transpose is an identity matrix.
Such that,
A. A’ = I
Matrix × transpose of matrix = identity matrix
Note- if |A| = 1, then we can say that matrix A is proper.
Examples: 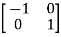 and
and 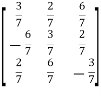 are the form of orthogonal matrices.
are the form of orthogonal matrices.
Unitary matrix-
A square matrix A is said to be unitary matrix if the product of the transpose of the conjugate of matrix A and matrix itself is an identity matrix.
Such that,
( ͞A)’ . A = I
For example:
A = 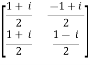 and its ( ͞A)’ =
and its ( ͞A)’ = 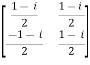
Then ( ͞A)’ . A = I
So that we can say that matrix A is said to be a unitary matrix.
The following transformation are defined as elementary transformations-
1. Interchange of any two rows (column)
2. Multiplication of any row or column by any non-zero scalar quantity k.
3. Addition to one row (column) of another row(column) multiplied by any non-zero scalar.
The symbol ~ is used for equivalence.
Elementary matrices-
If we get a square matrix from an identity or unit matrix by using any single elementary transformation is called elementary matrix.
Note- Every elementary row transformation of a matrix can be affected by pre multiplication with the corresponding elementary matrix.
The method of finding inverse of a non-singular matrix by using elementary transformation-
Working steps-
1. Write A = IA
2. Perform elementary row transformation of A of the left side and I on right side.
3. Apply elementary row transformation until ‘A’ (left side) reduces to I, then I reduces to 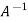
Example-1: Find the inverse of matrix ‘A’ by using elementary transformation-
A = 
Sol. Write the matrix ‘A’ as-
A = IA
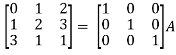
Apply 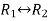 , we get
, we get
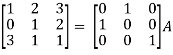
Apply 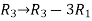
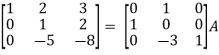
Apply 
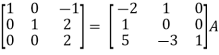
Apply 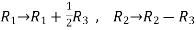
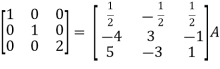
Apply 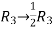
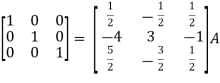
So that,
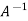 =
= 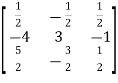
Example-2: Find the inverse of matrix ‘A’ by using elementary transformation-
A = 
Sol. Write the matrix ‘A’ as-
A = IA

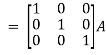
Apply 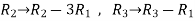
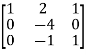
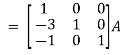
Apply 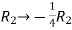
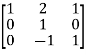
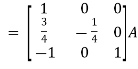
Apply 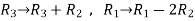

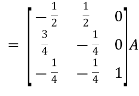
Apply 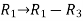

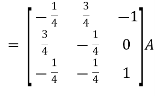
So that
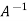 =
= 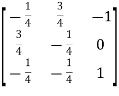
Rank of a matrix by echelon form-
The rank of a matrix (r) can be defined as –
1. It has atleast one non-zero minor of order r.
2. Every minor of A of order higher than r is zero.
Example: Find the rank of a matrix M by echelon form.
M = 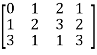
Sol. First we will convert the matrix M into echelon form,
M = 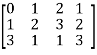
Apply, 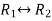 , we get
, we get
M = 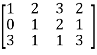
Apply 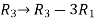 , we get
, we get
M = 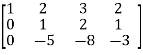
Apply 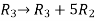
M = 
We can see that, in this echelon form of matrix, the number of non – zero rows is 3.
So that the rank of matrix X will be 3.
Example: Find the rank of a matrix A by echelon form.
A = 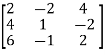
Sol. Convert the matrix A into echelon form,
A = 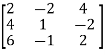
Apply 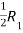
A = 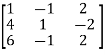
Apply 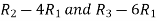 , we get
, we get
A = 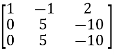
Apply 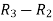 , we get
, we get
A = 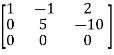
Apply 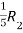 ,
,
A = 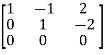
Apply 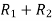 ,
,
A = 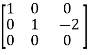
Therefore the rank of the matrix will be 2.
Example: c
Example: Find the rank of the following matrices by echelon form?
Let A = 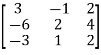
Applying 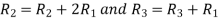
A 
Applying 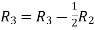
A 
Applying 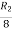
A 
Applying 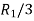
A 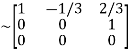
It is clear that minor of order 3 vanishes but minor of order 2 exists as 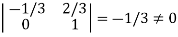
Hence rank of a given matrix A is 2 denoted by 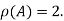
2. 
Let A = 
Applying 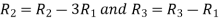

Applying 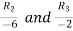
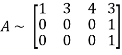
Applying 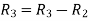
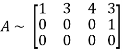
The minor of order 3 vanishes but minor of order 2 non zero as 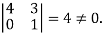
Hence the rank of matrix A is 2 denoted by 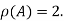
3. 
Let A = 
Apply 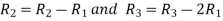

Apply 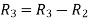

Apply 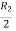
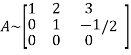
It is clear that the minor of order 3 vanishes where as the minor of order 2 is non zero as 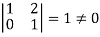
Hence the rank of given matrix is 2 i.e. 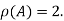
Rank of a matrix by normal form-
Any matrix ‘A’ which is non-zero can be reduced to a normal form of ‘A’ by using elementary transformations.
There are 4 types of normal forms –

The number r obtained is known as rank of matrix A.
Both row and column transformations may be used in order to find the rank of the matrix.
Note-Normal form is also known as canonical form
Example: reduce the matrix A to its normal form and find rank as well.

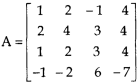
Sol. We have,

We will apply elementary row operation,
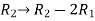
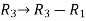
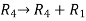
We get,

Now apply column transformation,
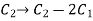
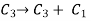
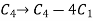
We get,

Apply
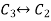 , we get,
, we get,
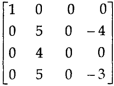
Apply 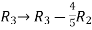 and
and 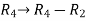

Apply 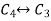

Apply 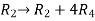 and
and 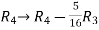

Apply 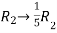 and
and 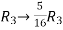

As we can see this is required normal form of matrix A.
Therefore the rank of matrix A is 3.
Example: Find the rank of a matrix A by reducing into its normal form.
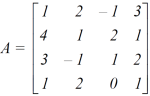
Sol. We are given,
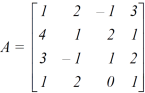
Apply
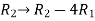
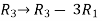
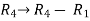
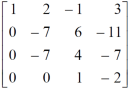

Apply
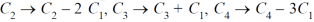
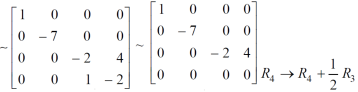
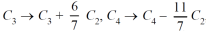
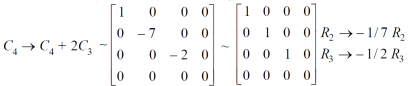
This is the normal form of matrix A.
So that the rank of matrix A = 3
Solution of homogeneous system of linear equations-
A system of linear equations of the form AX = O is said to be homogeneous , where A denotes the coefficients and of matrix and and O denotes the null vector.
Suppose the system of homogeneous linear equations is ,



It means ,
AX = O
Which can be written in the form of matrix as below,
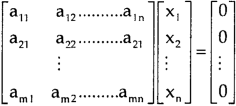
Note- A system of homogeneous linear equations always has a solution if
1. r(A) = n then there will be trivial solution, where n is the number of unknown,
2. r(A) < n , then there will be an infinite number of solution.
Example: Find the solution of the following homogeneous system of linear equations,
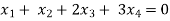
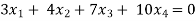
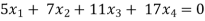
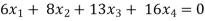
Sol. The given system of linear equations can be written in the form of matrix as follows,
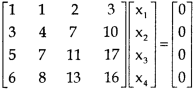
Apply the elementary row transformation,
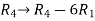 , we get,
, we get,
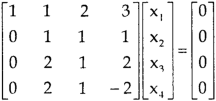
 , we get
, we get
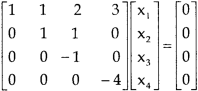
Here r(A) = 4, so that it has trivial solution,
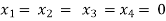
Example: Find out the value of ‘b’ in the system of homogenenous equations-
2x + y + 2z = 0
x + y + 3z = 0
4x + 3y + bz = 0
Which has
(1) trivial solution
(2) non-trivial solution
Sol. (1)
For trivial solution, we already know that the values of x , y and z will be zerp, so that ‘b’ can have any value.
Now for non-trivial solution-
(2)
Convert the system of equations into matrix form-
AX = O
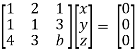
Apply 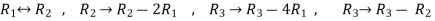 respectively , we get the following resultant matrices
respectively , we get the following resultant matrices
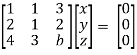
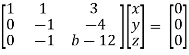
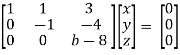
For non-trivial solutions , r(A) = 2 < n
b – 8 = 0
b = 8
Solution of non-homogeneous system of linear equations-
Example-1: check whether the following system of linear equations is consistent of not.
2x + 6y = -11
6x + 20y – 6z = -3
6y – 18z = -1
Sol. Write the above system of linear equations in augmented matrix form,
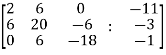
Apply 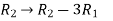 , we get
, we get
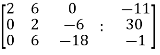
Apply 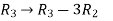
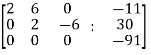
Here the rank of C is 3 and the rank of A is 2
Therefore both ranks are not equal. So that the given system of linear equations is not consistent.
Example: Check the consistency and find the values of x , y and z of the following system of linear equations.
2x + 3y + 4z = 11
X + 5y + 7z = 15
3x + 11y + 13z = 25
Sol. Re-write the system of equations in augmented matrix form.
C = [A,B]
That will be,
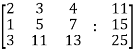
Apply 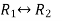
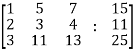
Now apply , 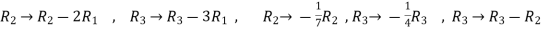
We get,
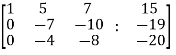 ~
~ 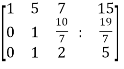 ~
~ 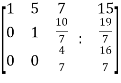
Here rank of A = 3
And rank of C = 3, so that the system of equations is consistent,
So that we can can solve the equations as below,
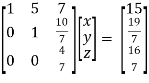
That gives,
x + 5y + 7z = 15 ……………..(1)
y + 10z/7 = 19/7 ………………(2)
4z/7 = 16/7 ………………….(3)
From eq. (3)
z = 4,
From 2,
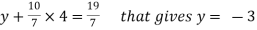
From eq.(1), we get
x + 5(-3) + 7(4) = 15
That gives,
x = 2
Therefore the values of x , y , z are 2 , -3 , 4 respectively.
There are two types of linear equations-
1. Consistent 2. Inconsistent
Let’s understand about these two types of linear equations[
Consistent –
If a system of equations has one or more than one solution, it is said be consistent.
There could be unique solution or infinite solution.
For example-
A system of linear equations-
2x + 4y = 9
x + y = 5
Has unique solution,
Where as,
A system of linear equations-
2x + y = 6
4x + 2y = 12
Has infinite solutions.
Inconsistent-
If a system of equations has no solution, then it is called inconsistent.
Consistency of a system of linear equations-
Suppose that a system of linear equations is given as-




This is the format as AX = B
Its augmented matrix is-
[A:B] = C
(1) consistent equations-
If Rank of A = Rank of C
Here, Rank of A = Rank of C = n ( no. Of unknown) – unique solution
And Rank of A = Rank of C = r , where r<n - infinite solutions
(2) inconsistent equations-
If Rank of A ≠ Rank of C
Example: Test the consistency of the following set of equations.
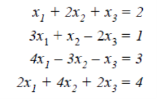
Sol. We can write the set of equations in matrix form :
-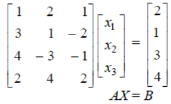
We have augmented matrix C = [A:B]
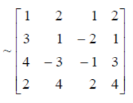
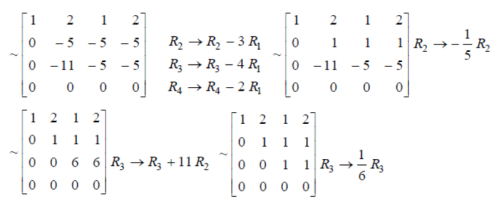
Here we know that,
Number of non-zero rows = Rank of matrix
R(C) = R(A) = 3
Hence the given system is consistent and has unique solution.
Example: test the consistency:
2x + 3y + 4z = 11 , x + 5y + 7z = 15 , 3x + 11y + 13z = 25
Sol. Here augmented matrix is given by,
C = [A:B]
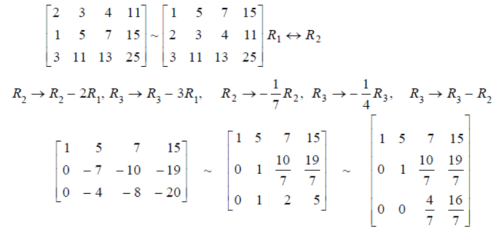
We notice here,
Rank of A= Rank of C = 3
Hence we can say that the system is consistent.
Suppose we have A = 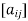 be an n × n matrix , then
be an n × n matrix , then
Characteristic equation- The equation |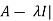 = 0 is called the characteristic equation of A , where |
= 0 is called the characteristic equation of A , where |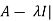 is called characteristic matrix of A. Here I is the identity matrix.
is called characteristic matrix of A. Here I is the identity matrix.
The determinant |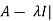 is called the characteristic polynomial of A.
is called the characteristic polynomial of A.
Characteristic roots- the roots of the characteristic equation are known as characteristic roots or Eigen values or characteristic values.
Important notes on characteristic roots-
1. The characteristic roots of the matrix ‘A’ and its transpose A’ are always same.
2. If A and B are two matrices of the same type and B is invertible then the matrices A and 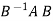 have the same characteristic roots.
have the same characteristic roots.
3. If A and B are two square matrices which are invertible then AB and BA have the same characteristic roots.
4. Zero is a characteristic root of a matrix if and only if the given matrix is singular.
Solved examples to find characteristics equation-
Example-1: Find the characteristic equation of the matrix A:
A = 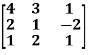
Sol. The characteristic equation will be-
|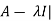 = 0
= 0
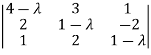 = 0
= 0
On solving the determinant, we get
(4-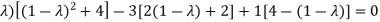
Or 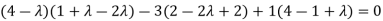
On solving we get,
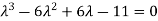
Which is the characteristic equation of matrix A.
Example-2: Find the characteristic equation and characteristic roots of the matrix A:
A = 
Sol. We know that the characteristic equation of the matrix A will be-
|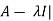 = 0
= 0
So that matrix A becomes,
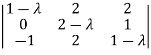 = 0
= 0
Which gives , on solving
(1-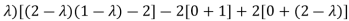 = 0
= 0
Or 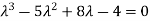
Or (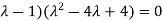
Which is the characteristic equation of matrix A.
The characteristic roots will be,
(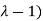 (
(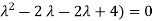
(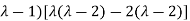
(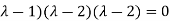
Values of 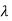 are-
are-
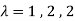
These are the characteristic roots of matrix A.
Example-3: Find the characteristic equation and characteristic roots of the matrix A:
A = 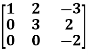
Sol. We know that, the characteristic equation is-
|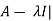 = 0
= 0
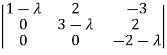 = 0
= 0
Which gives,
(1-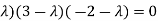
Characteristic rootsare- 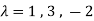
Eigen values and Eigen vectors-
Let A is a square matrix of order n. The equation formed by
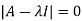
Where I is an identity matrix of order n and 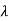 is unknown. It is called characteristic equation of the matrix A.
is unknown. It is called characteristic equation of the matrix A.
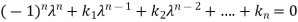
The values of the 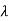 are called the root of the characteristic equation, they are also known as characteristics roots or latent root or Eigen values of the matrix A.
are called the root of the characteristic equation, they are also known as characteristics roots or latent root or Eigen values of the matrix A.
Corresponding to each Eigen value there exist vectors X,
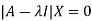
Called the characteristics vectors or latent vectors or Eigen vectors of the matrix A.
Note: Corresponding to distinct Eigen value we get distinct Eigen vectors but in case of repeated Eigen values we can have or not linearly independent Eigen vectors.
If 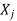 is Eigen vectors corresponding to Eigen value
is Eigen vectors corresponding to Eigen value 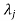 then
then 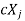 is also Eigen vectors for scalar c.
is also Eigen vectors for scalar c.
Properties of Eigen Values:
- The sum of the principal diagonal element of the matrix is equal to the sum of the all Eigen values of the matrix.
Let A be a matrix of order 3 then 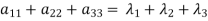
2. The determinant of the matrix A is equal to the product of the all Eigen values of the matrix then 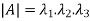 .
.
3. If 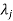 is the Eigen value of the matrix A then 1/
is the Eigen value of the matrix A then 1/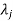 is the Eigen value of the
is the Eigen value of the  .
.
4. If 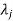 is the Eigen value of an orthogonal matrix, then 1/
is the Eigen value of an orthogonal matrix, then 1/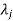 is also its Eigen value.
is also its Eigen value.
5. If 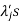 are the Eigen values of the matrix A then
are the Eigen values of the matrix A then 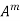 has the Eigen values
has the Eigen values 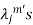 .
.
Example1: Find the sum and the product of the Eigen values of 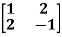 ?
?
Sol. The sum of Eigen values = the sum of the diagonal elements
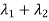 =1+(-1)=0
=1+(-1)=0
The product of the Eigen values is the determinant of the matrix
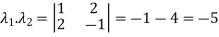
On solving above equations we get 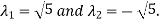
Example2: Find out the Eigen values and Eigen vectors of 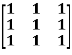 ?
?
Sol. The Characteristics equation is given by 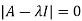
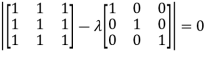
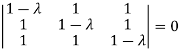
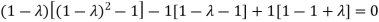
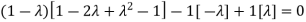
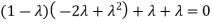
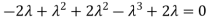
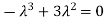
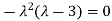
Or 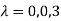
Hence the Eigen values are 0,0 and 3.
The Eigen vector corresponding to Eigen value 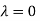 is
is
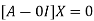
Where X is the column matrix of order 3 i.e.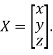
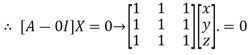
This implies that 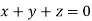
Here number of unknowns are 3 and number of equation is 1.
Hence we have (3-1)=2 linearly independent solutions.
Let 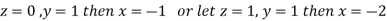
Thus the Eigen vectors corresponding to the Eigen value 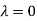 are (-1,1,0) and (-2,1,1).
are (-1,1,0) and (-2,1,1).
The Eigen vector corresponding to Eigen value 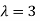 is
is
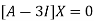
Where X is the column matrix of order 3 i.e.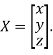
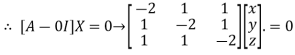
This implies that 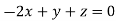
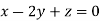
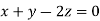
Taking last two equations we get
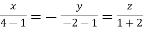
Or 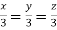
Thus the Eigen vectors corresponding to the Eigen value 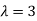 are (3,3,3).
are (3,3,3).
Hence the three Eigen vectors obtained are (-1,1,0), (-2,1,1) and (3,3,3).
Example3: Find out the Eigen values and Eigen vectors of 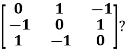
Sol. Let A =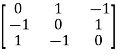
The characteristics equation of A is 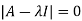 .
.
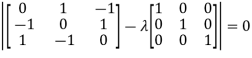
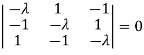
Or 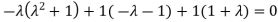
Or 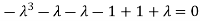
Or 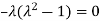
Or 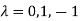
The Eigen vector corresponding to Eigen value 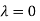 is
is
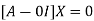
Where X is the column matrix of order 3 i.e.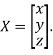
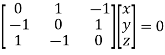
Or 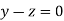
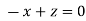
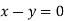
On solving we get 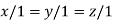
Thus the Eigen vectors corresponding to the Eigen value 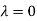 is (1,1,1).
is (1,1,1).
The Eigen vector corresponding to Eigen value 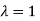 is
is
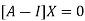
Where X is the column matrix of order 3 i.e.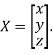
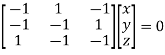
Or 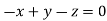
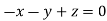
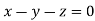
On solving 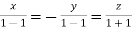 or
or 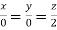 .
.
Thus the Eigen vectors corresponding to the Eigen value 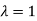 is (0,0,2).
is (0,0,2).
The Eigen vector corresponding to Eigen value 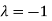 is
is
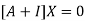
Where X is the column matrix of order 3 i.e.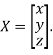
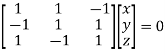
Or 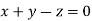
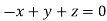
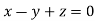
On solving we get 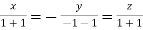 or
or 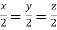 .
.
Thus the Eigen vectors corresponding to the Eigen value 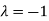 is (2,2,2).
is (2,2,2).
Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).
Cayley-Hamilton theorem states that every square matrix A when substituted in its characteristics equation, will satisfies it.
Let A is a square matrix of order n. The characteristic equation of the matrix A.
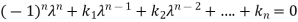
Then according to Cayley-Hamilton theorem
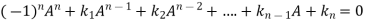
We can also find the inverse of A ,
Multiplying 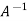 on both side of above equation we get
on both side of above equation we get
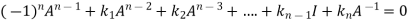
Or 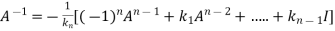
Example1: Verify the Cayley-Hamilton theorem and find the inverse.
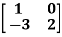 ?
?
Sol. Let A =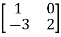
The characteristics equation of A is 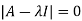
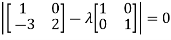
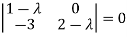
Or 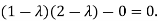
Or 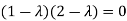
Or 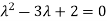
By Cayley-Hamilton theorem 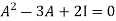
L.H.S: 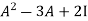
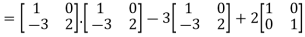
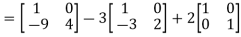
= 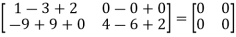 =0=R.H.S
=0=R.H.S
Multiply both side by 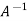 on
on 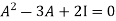
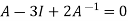
Or 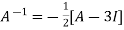
Or 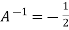 [
[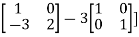
Or 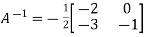
Example2: Verify the Cayley-Hamilton theorem and find the inverse.
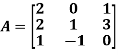
Sol. The characteristics equation of A is 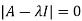
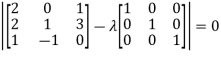
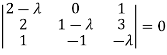
Or 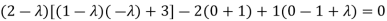
Or 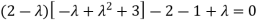
Or 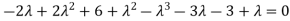
Or 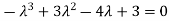
Or 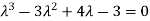
By Cayley-Hamilton theorem 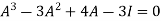
L.H.S. 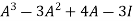
=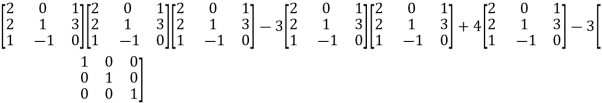
=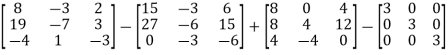
=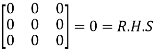
Multiply both side with 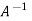 in
in 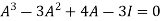
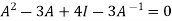
Or 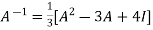
Or 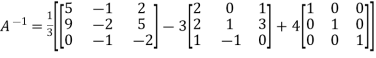
=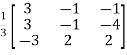
Example-3: Verify Cayley-Hamilton theorem for matrix A:
A = 
Sol. Characteristic equation of matrix A will be, 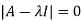
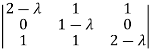 = 0
= 0
(2-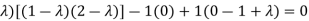
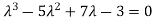
According to Cayley-Hamilton theorem,
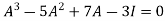 …………..(1)
…………..(1)
Here we need to verify eq.(1)-
First we will find A² -
A² = 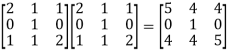
Now,
A³ = A².A = 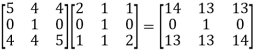
Equation (1) becomes,
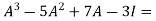
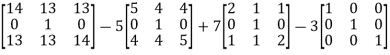
= 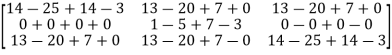
= 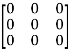
Hence the Cayley-Hamilton theorem is verified.
Example-4: Using Cayley-Hamilton theorem, find 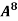 , if A =
, if A = 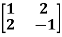 ?
?
Sol. Let A =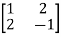
The characteristics equation of A is 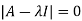
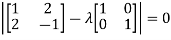
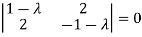
Or 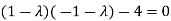
Or 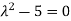
By Cayley-Hamilton theorem 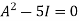
L.H.S. 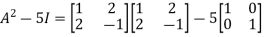
=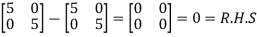
By Cayley-Hamilton theorem we have 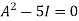
Multiply both side by 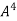
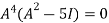 .
.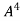
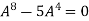
Or 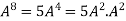
=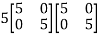
=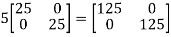
Matrices has very wide applications in production, electricity , nets of roads etc.
Example-1: Find the currents 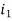 ,
, 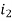 ,
, 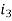 in the following electric circuit.
in the following electric circuit.
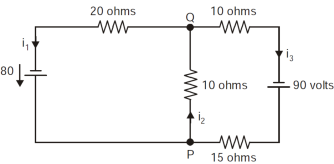
Sol. In order to find out the result first we will go through Kirchoff’s current law and voltage law –
Kirchoff’s current law- The sum of the in flowing currents equals to the sum of the out flowing currents at any points of the circuit.
Kirchoff’s voltage law- The sum of all voltages drops equals the impressed electromotive force in a closed loop.
Node P gives- 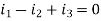
Node Q gives- 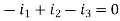
Right loop gives- 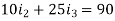
Left loop gives- 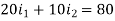
We have these four equations.
Let’s solve these equations by matrix method-
The augmented matrix will be-
[A : B] = 
Apply 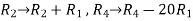

Apply 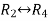

Apply 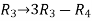
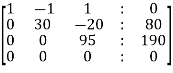
Apply 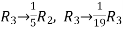

Now we get-
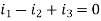
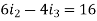
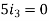
On solving these, we get-