UNIT- 3
QUANTUM MECHANICS
As we know in the Photoelectric Effect, the Compton Effect, and the pair production effect—radiation exhibits particle-like characteristics in addition to its wave nature. In 1923 de Broglie took things even further by suggesting that this wave–particle duality is not restricted to radiation, but must be universal.
In 1923, the French physicist Louis Victor de Broglie (1892-1987) put forward the bold hypothesis that moving particles of matter should display wave-like properties under suitable conditions.
All material particles should also display dual wave–particlebehaviour. That is, the wave–particle duality present in light must also occur in matter.
So, starting from the momentum of a photon p = hν/c = h/λ.
We can generalize this relation to any material particle with nonzero rest mass. Each material particle of momentum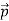 
behaves as a group of waves(matter waves) whose wavelength λand wave vector 
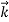are governed by the speed and mass of the particle. De Broglie proposed that the wave length λ associated with a particle of momentum p is given as where m is the mass of the particle and v its speed.
λ = 
=
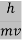…….(1) 
= 
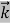…….(2)
Where ℏ = h/2π. The expression known as the deBroglie relation connects the momentum of a particle with the wavelength and wave vector of the wave corresponding to this particle.The wavelength λ of the matter wave is called de Broglie wavelength. The dual aspect of matter is evident in the de Broglie relation.
λ is the attribute of a wave while on the right hand side the momentum p is a typical attribute of a particle. Planck’s constant h relates the two attributes.Equation (1) for a material particle is basically a hypothesis whose validity can be tested only by experiment.
However, it is interesting to see that it is satisfied also by a photon. For a photon, as we have seen, p = hν/c.
Therefore
= 
= λ
Example:What is the frequency of a photon with energy of 4.5 eV?
Solution:
E = (4.5 eV) x (1.60 x 10-19 J/eV) = 7.2 x 10-19 J
E = hf
h = 6.63 x 10-34 J x s
f = E / h = (7.2 x 10-19 J) / (6.63 x 10-34 J x s)
f = 1.1 x 1015 Hz
De Broglie’s Hypothesis: MatterWaves
Matter waves: According to De-Broglie, a wave is associated with each moving particle which is called matter waves.
As we know in the photoelectric effect, the Compton Effect, and the pair production effect radiation exhibits particle-like characteristics in addition to its wave nature. In 1923 de Broglie took things even further by suggesting that this wave–particle duality is not restricted to radiation, but must be universal:
All material particles should also display a dual wave–particlebehaviour.
That is, the wave–particle duality present in light must also occur in matter. So, starting from the momentum of a photon p= hν /c =h/λ, we can generalize this relation to any material particle with nonzero rest mass: each material particle of momentum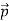
behaves as a group of waves (matter waves) whose wavelength λand wave vector
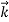are governed by the speed and mass of the particle.
λ = 
= 
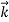Wave has wavelength λhere h is Planck's constant and p is the momentum of the moving particle.
We have seen that microscopic particles, such as electrons, display wave behaviour. What aboutmacroscopic objects? Do they also display wave features? They surely do. Although macro-scopic material particles display wave properties, the corresponding wavelengths are too smallto detect; being very massive, macroscopic objects have extremely small wavelengths.
At the microscopic level, however, the waves associated with material particles are of the same size or exceed the size of the system. Microscopic particles therefore exhibit clearly noticeable wave-like aspects.
The general rule is: whenever the de Broglie wavelength of an object is in the range of, or exceeds, its size, the wave nature of the object is detectable and hence cannot be neglected.
But if its de Broglie wavelength is much too small compared to its size, the wave behaviour of this object is undetectable.
For a quantitative illustration of this general rule, let us calculate in the following example the wavelengths corresponding to two particles, one microscopic (electron) and the other macroscopic(ball).
Example:What is the de Broglie wavelength associated with (a) an electron moving with a speed of 5.4×106 m/s, and (b) a ball of mass 150 g travelling at 30.0 m/s?
Solution:
(a)For the electron:
Mass m = 9.11×10–31 kg, speed v = 5.4×106 m/s.
Then, momentum
p = m v = 9.11×10–31 kg × 5.4 × 106 (m/s)
p = 4.92 × 10–24 kg m/s
De Broglie wavelength, λ = h/p = 6.63 x 10-34Js/ 4.92 × 10–24kg m/s
λ= 0.135 nm
(b)For the ball:
Mass m’ = 0.150 kg,
Speed v ’= 30.0 m/s.
Then momentum p’ = m’ v’= 0.150 (kg) × 30.0 (m/s)
p’= 4.50 kg m/s
De Broglie wavelength λ’ = h/p’ =6.63 x 10-34Js/ 4.50kg m/s =1.47 ×10–34 m
The de Broglie wavelength of electron is comparable with X-raywavelengths. However, for the ball it is about 10–19 times the size of the proton, quite beyond experimental measurement.
Characteristics of Matter waves:
- Matter waves are the waves associated with matter in motion. Wavelength of the matter waves is given by λ=h/p.
- Matter waves are not progressive waves. They are localized waves.
- Matter waves are not single waves. They are group of waves (wave packet) assumed formed due to the superposition of two or more progressive waves.
- Matter waves called pilot waves and they represent the direction of propagation of matter.
- Unlike electromagnetic waves, matter waves will not have constant speed. The speed of matter waves depends on the mass of the particle.
- Vg x Vp=C2 shows that Vp, phase velocity of matter waves is greater than velocity of light. This shows that matter waves not physical waves
- Lighter the particle, greater is the De-Broglie wave length.
- The faster the particle moves, the smaller is its De-Broglie wave length.
- The De-Broglie wave length of a particle in independent of the charge or nature of the particle.
- The matter waves are not electromagnetic in nature. The electromagnetic waves are produced only by charged particle.
Schrodinger wave equation, is the fundamental equation of quantum mechanics, same as the second law of motion is the fundamental equation of classical mechanics. This equation has been derived by Schrodinger in 1925 using the concept of wave function on the basis of de-Broglie wave and plank’s quantum theory.
Let us consider a particle of mass m and classically the energy of a particleis the sum of the kinetic and potential energies. We will assume that the potential is a function of only x.
So We have
E=K+V=
mv2+V(x) =
+V(x) ……….. (1)
By de Broglie’s relation we know that all particles can be represented as waves with frequency ω and wave number k, and that E= ℏω and p= ℏk.
Using this equation (1) for the energy will become
ℏω =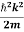 
+V(x) ……….. (2)
A wave with frequencyωand wavenumberkcan be written as usual as
ψ(x, t) =Aei(kx−ωt) ……….. (3)
The above equation is for one dimensional and for three dimensional we can write it as
ψ(r, t) =Aei(k·r−ωt) ……….. (4)
But here we will stick to one dimension only.
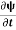=−iωψ⇒ ωψ=
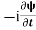……….. (5)
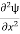=−k2ψ ⇒k2ψ = - 
……….. (6)
If we multiply the energy equation in Eq. (2) byψ, and using(5) and (6) , weobtain
ℏ(ωψ) =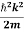 
ψ+V(x)ψ⇒ 
= - 
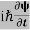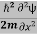+ V(x) ψ……….. (7)
This is the time-dependent Schrodinger equation.
If we put the x and t in above equation then equation (7) takes the form as given below
= - 
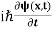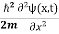+ V(x) ψ(x,t) ……….. (8)
In 3-D, thexdependence turns into dependence on all three coordinates (x, y, z) and the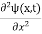
term becomes∇2ψ.
The term |ψ(x)|2gives the probability of finding the particleat positionx.
Let us again take it assimply a mathematical equation, then it’s just another wave equation. However We already know the solution as we used this functionψ(x, t) =Aei(kx−ωt) to produce Equations (5), (6) and (7)
But let’s pretend that we don’t know this, and let’s solve theSchrodinger equation as if we were given to us.As always, we will guess an exponential solution by looking at exponential behaviour in the time coordinate, our guess isψ(x, t) =e−iωtf(x) putting this into Equation (7) and cancelling thee−iωtyields
= - 
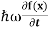+ V(x)f(x) ……….. (9)
We already know that E=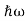
. However ψ(x, t) is general convention to also use the letterψto denote the spatial part. So wewill now replacef(x) withψ(x)
Eψ = - 
+ V(x) ψ ……….. (10)
This is called the time-independent Schrodinger equation.
It is not possible to measure all properties of a quantum system precisely. Max Born suggested that the wave function was related to the probability that an observable has a specific value.
In any physical wave if ‘A’ is the amplitude of the wave, then the energy density i.e., energy per unit volume is equal to ‘A2’. Similar interpretation can be made in case of mater wave also. In matter wave, if ‘Ψ‘is the wave function of matter waves at any point in space, then the particle density at that point may be taken as proportional to ‘Ψ2’ . Thus Ψ2 is a measure of particle density.
According to Max Born ΨΨ*=Ψ2gives the probability of finding the particle in the state ‘Ψ’. i.e., ‘Ψ2’ is a measure of probability density. The probability of finding the particle in a volume( dv=dxdydz) is given by
= 
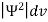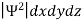
Since the particle has to be present somewhere, total probability of finding the particle somewhere is unity i.e., particle is certainly to be found somewhere in space. i.e
=1
Or 
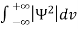=1
This condition is called Normalization condition. A wave function which satisfies this condition is known as normalized wave function.
The wave function, at a particular time, contains all the information that anybody at that time can have about the particle. But the wave function itself has no physical interpretation. It is not measurable. However, the square of the absolute value of the wave function has a physical interpretation. We interpret |ψ(x,t)|2 as a probability density, a probability per unit length of finding the particle at a time t at position x.
The wave function ψ associated with a moving particle is not an observable quantity and does not have any direct physical meaning. It is a complex quantity. The complex wave function can be represented as
ψ(x, y, z, t) = a + ib
And its complex conjugate as
ψ*(x, y, z, t) = a – ib.
The product of wave function and its complex conjugate is
ψ(x, y, z, t)ψ*(x, y, z, t) = (a + ib) (a – ib) = a2 + b2
a2 + b2is a real quantity.
However, this can represent the probability density of locating the particle at a place in a given instant of time.
The positive square root of ψ(x, y, z, t) ψ*(x, y, z, t) is represented as |ψ(x, y, z, t)|, called the modulus of ψ. The quantity |ψ(x, y, z, t)|2 is called the probability.This interpretation is possible because the product of a complex number with its complex conjugate is a real, non-negative number.
We should be able to find the particle somewhere, we should only find it at one place at a particular instant, and the total probability of finding it anywhere should be one.
For the probability interpretation to make sense, the wave function must satisfy certain conditions.
- The wave function must be single valued at each point.
- The probability of finding the particle at time t in an interval ∆x must be some number between 0 and 1.
- ψ must be finite everywhere.
- ψmust be continuous everywhere and
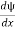must also be continuous everywhere except where V(x) is infinite. - ψ (x) must vanish ψ
0 as x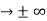
. - The wave function should satisfy the normalization condition. Normalization condition of a wave function ψ is mathematical statement of existence of the particle somewhere.so that if we sum up all possible values ∑|ψ(xi,t)|2∆xi we must obtain 1. The total probability of finding the particle anywhere must be one. Normalization condition is given as
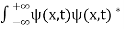dx =1
Only wave function with all these properties can yield physicallymeaningful result.
Physical significance of wave function
- The wave function ‘Ѱ’ has no physical meaning. It is a complex quantity representing the variation of a matter wave.
- The wave function Ѱ(r,t) describes the position of particle with respect to time .
- It can be considered as ‘probability amplitude’ since it is used to find the location of the particle.
- The square of the wave function gives the probability densityof the particle which is represented by the wave function itself.
- More the value of probability density, more likely to find the particle in that region.
The Schrodinger equation also known as Schrodinger’s wave equation is a partial differential equation that describes the dynamics of quantum mechanical systems by the wave function. The trajectory, the positioning, and the energy of these systems can be retrieved by solving the Schrodinger equation.
All of the information for a subatomic particle is encoded within a wave function. The wave function will satisfy and can be solved by using the Schrodinger equation. The Schrodinger equation is one of the fundamental axioms that are introduced in undergraduate physics.
Particle in a One Dimensional Deep Potential Well
Let us consider a particle of mass ‘m’ in a deep well restricted to move in a one dimension (say x). Let us assume that the particle is free inside the well except during collision with walls from which it rebounds elastically.
The potential function is expressed as
V= 0 for 0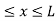
………. (1)
V=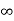 
for x <0, x>L ………. (2)
Figure : Particle in deep potential well
The probability of finding the particle outside the well is zero (i.e.Ѱ =0)
Inside the well, the Schrödinger wave equation is written as
ψ +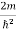
Eψ =0 …………….(2)
Substituting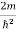
E = k2 …………….(3)
Writing the SWE for 1-D we get
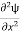+k2ψ =0 …………….(4)
The general equation of above equation may be expressed as
ψ = Asin (kx + ϕ) …………….(5)
Where A and ϕ are constants to be determined by boundary conditions
Condition I: We have ψ = 0 at x = 0, therefore from equation
0= A sinϕ
As A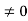 
then sinϕ =0 orϕ=0 …………….(6)
Condition II:Further ψ = 0 at x = L, andϕ=0,therefore from equation(5)
0= AsinkL
As A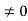 
then sinkL =0 orkL=nπ
k =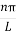 
…………….(7)
Where n= 1,2,3,4………
Substituting the value of k from (7) to (3)
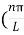)2 = 
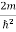E
This gives energy of level
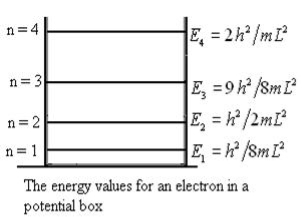
En =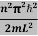
n=1,2,3,4…so on …………….(8)
From equation En is the energy value (Eigen Value) of the particle in a well.
It is clear that the energy values of the particle in well are discrete not continuous.
Using (6) and (7) equation (5) becomes, the corresponding wave functions will be
ψ =ψn= Asin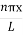
…………….(9)
The probability density
|ψ(x,t)|2 =ψψ*
|ψ(x,t)|2=A2sin2
…………….(10)
The probability density is zero at x = 0 and x = L. Since the particle is always within the well
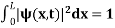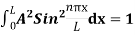
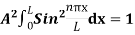
…………….(1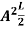1)
=1
A =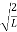
Substituting A in equation (9) we get
ψ =ψ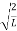n= 
sin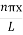
n=1,2,3,4….. …………….(12)
The above equation (12) is normalized wave function orEigen function belonging to energy value En
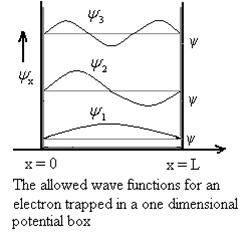Figure: Wave function for Particle
A Free Particle
A particle is said to be free when no external force is acting on during its motion in the given region of space, and its potential energy V is constant.
Let us consider an electro is freely moving in space in positive x direction and not acted by any force, there potential will be zero. The Schrodinger wave equation reduces to
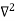ψ +
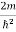Eψ =0
Substituting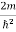
E = k2
As the electron is moving in one direction (say x axis), then the above equation can be written as
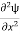+k2ψ =0
The general solution of the equation (2) is of the formψ = ψ0e-iωt
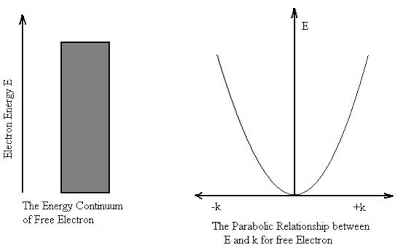
The electron is not bounded and hence there are no restrictions on k. This implies that all the values of energy are allowed. The allowed energy values form a continuum and are given by
E =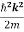 
The wave vector k describes the wave properties of the electron.
It is seen from the relation that E 
k2Thus the plot of E as a function of k gives a parabola.
The momentum is well defined and in this case given by
pxψ =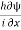
Therefore, according to uncertainty principle it is difficult to assign a position to the electron.
