UNIT- 4
WAVE OPTICS
INTERFERENCE
Interference in light waves occurs whenever two or more waves overlap at a given point.
TYPES OF INTERFERENCE
Interference of light waves can be either constructive interference or destructive interference.
- Constructive Interference: Constructive interference takes place when the crest of one wave falls on the crest of another wave such that the amplitude is maximum. These waves will have the same displacement and are in the same phase.
- Destructive Interference: In destructive interference the crest of one wave falls on the trough of another wave such that the amplitude is minimum. The displacement and phase of these waves are not the same.
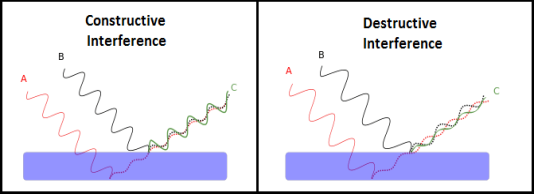
Figure 1
We know that the superposition of two mechanical waves can be constructive or destructive. In constructive interference, the amplitude of the resultant wave at a given position or time is greater than that of either individual wave, whereas in destructive interference, the resultant amplitude is less than that of either individual wave.
Light waves also interfere with each other. Fundamentally, all interference associated with light waves arises when the electromagnetic fields that constitute the individual waves combine.
If two light bulbs are placed side by side, no interference effects are observed because the light waves from one bulb are emitted independently of those from the other bulb. The emissions from the two light bulbs do not maintain a constant phase relationship with each other over time. Light waves from an ordinary source such as a light bulb undergo random phase changes in time intervals less than a nanosecond.
Therefore, the conditions for constructive interference, destructive interference, or some intermediate state are maintained only for such short time intervals. Because the eye cannot follow such rapid changes, no interference effects are observed. Such light sources are said to be incoherent.
The principle of superposition says:
When two or more waves cross at a point, the displacement at that point is equal to the sum of the displacements of the individual waves.
The individual wave displacements may be positive or negative. If the displacements are vectors, then the sum is calculated by vector addition.
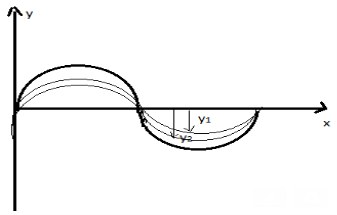
Figure 2
Superposition is an important idea that can explain phenomena including interference, diffraction and standing waves. It works for any type of wave (sound waves, water surface waves, electromagnetic waves...) but only works under certain conditions, which we describe below.
When the waves pass beyond a point of intersection, they separate out again and are unaffected.
The principle of superposition can be applied to any type of wave providing that:
- The waves being superposed are of the same type (e.g. All are electromagnetic waves)
- The medium that the waves are propagating through behaves linearly, i.e. when part of the medium has twice the displacement then it has twice the restoring force. This is usually true when the amplitudes are relatively small. For example, for waves on water, it is a good approximation for small ripples on a pond whose amplitude is much smaller than their wavelength.
If the waves are also coherent - i.e. if they all have the same frequency and a constant phase difference - then the superposition resembles another wave with the same frequency.
Considering two waves, travelling simultaneously along the same stretched string in opposite directions as shown in the figure above. We can see images of waveforms in the string at each instant of time. It is observed that the net displacement of any element of the string at a given time is the algebraic sum of the displacements due to each wave.
Let us say two waves are travelling alone and the displacements of any element of these two waves can be represented by y1(x, t) and y2(x, t). When these two waves overlap, the resultant displacement can be given as y(x,t).
Mathematically, y (x, t) = y1(x, t) + y2(x, t)
As per the principle of superposition, we can add the overlapped waves algebraically to produce a resultant wave. Let us say the wave functions of the moving waves are
y1 = f1(x–vt),
y2 = f2(x–vt)
……….
yn = fn (x–vt)
Then the wave function describing the disturbance in the medium can be described as
y = f1(x – vt)+ f2(x – vt)+ …+ fn(x – vt)
Or, y= 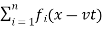
Let us consider a wave travelling along a stretched string given by,
y1(x,t) = A sin (kx – ωt)
And another wave, shifted from the first by a phase φ, given as
y2(x, t) = A sin (kx – ωt + ϕ)
From the equations we can see that both the waves have the same angular frequency, same angular wave number k, hence the same wavelength and the same amplitude A.
Now, applying the superposition principle, the resultant wave is the algebraic sum of the two constituent waves and has displacement
y(x, t) = A sin (kx – ωt) + A sin (kx – ωt + ϕ)
As, sin A + sin B = 2sin (A+B)/2 .cos (A−B)/2
The above equation can be written as,
y(x, t) = [2A cos ϕ /2 ] sin (kx − ωt + ϕ /2)
The resultant wave is a sinusoidal wave, travelling in the positive X direction, where the phase angle is half of the phase difference of the individual waves and the amplitude as [2cos ϕ /2] times the amplitudes of the original waves.
Hence, the superposition of waves can lead to the following three effects:
- Whenever two waves having the same frequency travel with the same speed along the same direction in a specific medium, then they superpose and create an effect known as the interference of waves.
- In a situation where two waves having similar frequencies move with the same speed along opposite directions in a specific medium, then they superpose to produce stationary waves.
- Finally, when two waves having slightly varying frequencies travel with the same speed along the same direction in a specific medium, they superpose to produce beats.
Two sources are said to be coherent when the waves emitted from them have the same frequency and constant phase difference.
Interference from such waves happen all the time, the randomly phased light waves constantly produce bright and dark fringes at every point. But, we cannot see them since they occur randomly. A point that has a dark fringe at one moment may have a bright fringe at the next moment. This cancels out the effect of the interference effect, and we see only an average brightness value. The interference is not said to be sustained since we cannot observe it.
Definition:- A predictable correlation of the amplitude and phase at any one point with other point is called coherence.
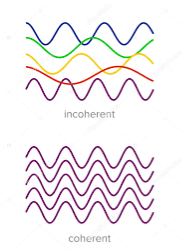
Figure 3
Two waves are said to be coherent, the waves must have
In case of convectional light, the property of coherence exhibits between a source and its virtual source where as in case of laser the property coherence exists between any two of more light waves.
There are two types of coherence
i) Temporal coherence
Ii) Spatial coherence
TEMPORAL COHERENCE (OR LONGITUDINAL COHERENCE):-
The predictable correlation of amplitude and phase at one point on the wave train w .r. t another point on the same wave train, then the wave is said to be temporal coherence
To understand this, let us consider two points P1 and P2 on the same wave train, which is continuous as in shown in figure.
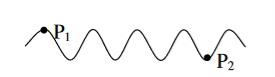
Figure 4
Suppose the phase and amplitude at any one point is known, then we can easily calculate the amplitude and phase for any other point on the same wave train by using the wave equation
y= a sin (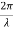 (ct-x))
(ct-x))
Where ‘a’ is the amplitude of the wave and ‘x’ is the displacement of the wave at any instant of time‘t’.
SPATIAL COHERENCE (OR TRANSVERSE COHERENCE)
The predictable correlation of amplitude and phase at one point on the wave train w. r .t another point on a second wave, then the waves are said to be spatial coherence (or transverse coherence)
Figure 5
In a sustained interference pattern, the position of maximum and minimum intensity regions remains constant with time. To obtain the sustained interference, the following conditions are required:
- The sources must be coherent, that is, they must maintain a constant phase with respect to each other.
- The two light sources must emit continuous waves of the same wavelength and having the same time period.
- The distance between the two sources of light must be small. This gives large fringe width so that the fringes are separately visible.
- The sources should be monochromatic, that is, of a single wavelength.
- The two light sources must emit waves in nearly the same direction.
- Light source must be a point source.
- The distance between the two sources and screen must be large. This gives again large fringe width so that the fringes are separately visible.
The phenomenon of interference may be grouped into two categories:
- Division of Wavefront: Under this category, the coherent sources are obtained by dividing the wavefront, originating from a common source, by employing mirrors, biprisms or lenses. This class of interference requires essentially a point source or a narrow slit source. The instruments used to obtain interference by division of wavefront are the Fresnel biprism, Fresnel mirrors, Lloyd's mirror, lasers, etc.
- Division of Amplitude: In this method, the amplitude of the incident beam is divided into two or more parts either by partial reflection or refraction. Thus we have coherent beams produced by division of amplitude. These beams travel different paths and are finally brought together to produce interference. The effects resulting from the superposition of two beams are referred to as two beam interference and those resulting from superposition of more than two beams are referred to as multiple beam interference. The interference in thin films, Newton's rings, and Michelson's interferometer are examples of two beam interference and Fabry-Perot's interferometer is an example of multiple beam interference.
FRESNEL’S BI-PRISM
The Fresnel double prism or biprism consists of two thin prisms joined at their bases, as shown in Figure 9. A single cylindrical wavefront impinges on both prisms. The top portion of the wavefront is refracted downward, and the lower segment is refracted upward. In the region of superposition, interference occurs. Here, again, two virtual sources S1 and S2 exist, separated by a distance a, which can be expressed in terms of the prism angle, where D>>d. The expression for the separation of the fringes is the same as before.
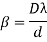
Where (D = a + b) is distance of the sources from the eyepiece.
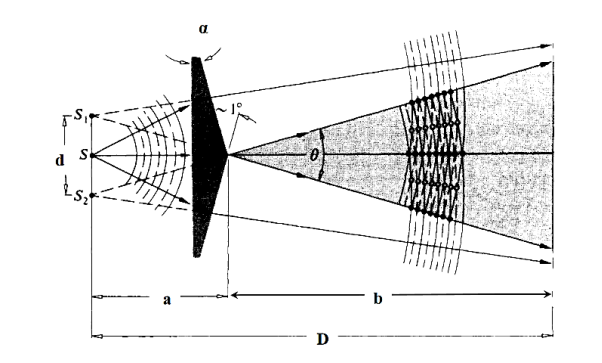
Figure 9
Light from monochromatic source is made to fall on a thin slit mounted vertically on a rigid optical bench fitted with a scale. The biprism and the screen (in this case an eye piece) are also mounted vertically. The eye piece can be moved in the plane perpendicular to the axis of bench using a micrometer based translation stage.
Applications of Fresnel's Biprism
Fresnel biprism can be used to determine the wavelength of a light source (monochromatic), thickness of a thin transparent sheet/ thin film, refractive index of medium etc.
Determination of wave length of light
As expression for fringe width is
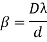
Biprism can be used to determine the wavelength of given monochromatic light using the expression.
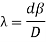
Determination of fringe width β:
When the fringes are observed in the field view of the eyepiece, the vertical cross-wire is made to coincide with the centre of one of the bright fringes. The position of the eyepiece is read on the scale, say x°. The micrometer screw of the eyepiece is moved slowly and the number of the bright fringes N that pass across the cross-wire is counted. The position of the cross-wire is again read, say xN. The fringe width is then given by
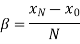
Determination of ( d ):
The value of d can be determined as follows. The deviation δ produced in the path of a ray by a thin prism is given by
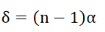
Where α is the refracting angle of the prism. For the figure, it is seen δ=θ∕2. Since d is very small, we can also write d = aθ
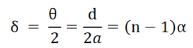
Interference Fringes with white light:
In the biprism experiment if the slit is illuminated by white light the interference pattern consists of a central white fringe flanked on its both sides by a few coloured fringes and general illumination beyond the fringes. The central white fringe is the zero-order fringe.
With monochromatic light all the bright fringes are of the same colour and it is not possible to locate zero-order fringe. Therefore, in order to locate the zero-order fringe the biprism is to be illuminated by white light.
Lateral Displacement of Fringes
The biprism experiment can be used to determine the thickness of given thin sheet of transparent material such as glass or mica. If a thin transparent sheet is introduced in the path of one of the two interfering beams, the fringe system gets displaced towards the beam in whose path the sheet is introduced. By measuring of displacement, the thickness of the sheet can be determined. Suppose S1 and S2 are the virtual coherent monochromatic sources. The point O is equidistant from S1 and S2, where we obtain the central bright fringe. Therefore, the optical path S1O=S2O. Let a transparent plate G of thickness t and refractive index n be introduced in the path of one of the beams (see figure 10). The optical path lengths S1O and S2O are now not equal and the central bright fringe shits to P from O. The light waves from S1to P travel partly in air and partly in the sheet G: the distance travelled in air is (S1P –t) and that in the sheet is t.
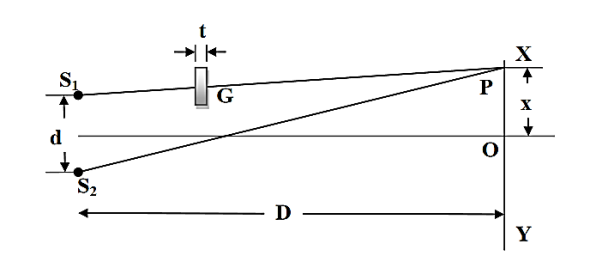
Figure 10
The optical path
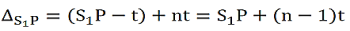
The optical path
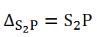
The optical path difference at P is
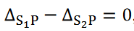
Since in the presence of the thin sheet, the optical path lengths S1P and S2P are equal and central zero fringe is obtained at P.
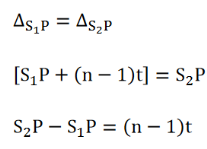
But according to the relation
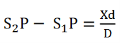
Where x is the lateral shift of the central fringe due to the introduction of the thin sheet.
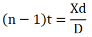
Hence, the thickness of the sheet is
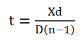
THIN FILM INTERFERENCE
A film of thickness from 0.5 to 10 μm is a transparent medium of glass, mica, air enclosed between glass, soap film, etc. When the light is made incident on this thin film partial reflection and partial refraction occur from the top surface of the film. The refracted beam travels in the medium and again suffers partial reflection and partial refraction at the bottom surface of the film. In this way several reflected and refracted rays are produces by a single incident ray. As they moves are superimposed on each other and produces interference pattern.

Figure 6
INTERFERENCE IN UNIFORM THIN FILM
Consider a thin film of uniform thickness ‘t’ and refractive index μ bounded between air. Let us consider monochromatic ray AB is made incident on the film, at B part of ray is reflected (R1) and a part is refracted along BC. At C The beam BC again suffer partial reflection and partial refraction; the reflected beam CD moves again suffer partial reflection and partial refraction at D. The refracted beam R2 moves in air. These two reflected rays R1 and R2 interfere to produce interference pattern.
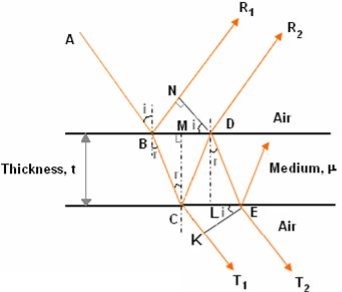
Figure 7
The optical path difference between the two reflected rays

In ΔBDN, sin i = BN / BD and BC = CD as ΔBMC ≡ ΔMCD, therefore
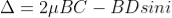
In ΔBMC, cos r = t /BC, therefore
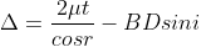
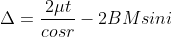
In ΔBMC, tan r = BM / t , therefore
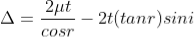
According to snell’s law 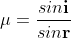
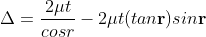
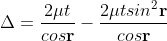
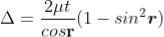
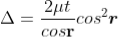
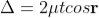 ................ (1)
................ (1)
Correction on account of phase change at reflection:
When a beam is reflected from a denser medium (ray R1 at B), a path change of λ/2 occur for the ray.
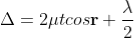 ….............. (2)
….............. (2)
Therefore the true path difference is
Condition of Maxima (Bright Fringe)
Maxima occur when path difference

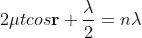
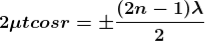 ............... (3)
............... (3)
Condition for Minima (Dark Fringe)
Minima occur when path difference
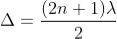
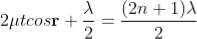
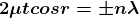 ................. (4)
................. (4)
INTERFERENCE IN THIN FILM (TRANSMITTED RAYS)
The optical path difference between transmitted rays T1 and T2 will be
This path difference is calculated in the same way as above to get
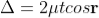 ................. (5)
................. (5)
Condition of Maxima (Bright Fringe)
Maxima occur when path difference,

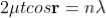 ................... (6)
................... (6)
Condition for Minima (Dark Fringe)
Minima occur when path difference,
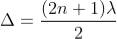
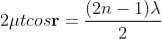 ............. (7)
............. (7)
The wedge shaped film has a thin film of varying thickness, having thickness zero at one end and increases at the other. The angle of wedge is θ.Wedge shaped film is one whose surface are inclined at an angle θ of refractive index μ bounded by non-uniform thickness.
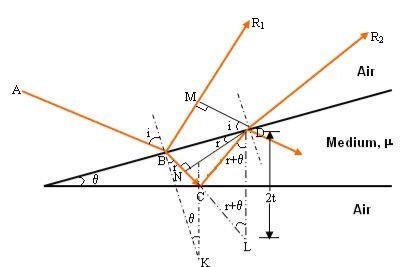
Figure 8
The optical path difference between the two reflected rays R1 and R2 will be

From the geometry
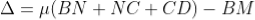
As in ΔBMD;
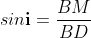
And in ΔBND
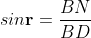
According Snell’s Law,
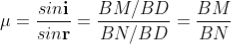
Or 
Thus 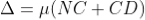
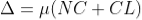
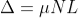
As in ΔNDL 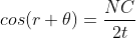
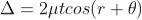
Correction on account of phase change at reflection: when a beam is reflected from a denser medium (ray R1 at B), a path change of  /2 occur for the ray.
/2 occur for the ray.
Therefore the true path difference is
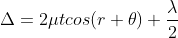
Condition of Maxima (Bright Fringe)
Maxima occur when path difference,
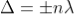
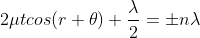
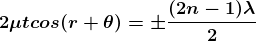
Condition for Minima (Dark Fringe)
Minima occur when path difference
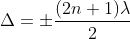
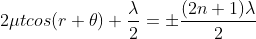

PRODUCTION OF COLOURS IN THIN FILMS
When a transparent thin film is illuminated with a white light, coloured fringes are observed. These fringes are due to the interference of light waves reflected from the top and bottom surface of the thin film. The path difference between the reflected waves depends on thickness t of the film, refractive index μ of the film and the angle of refraction r. The reflected light from the thin film of particular thickness t should satisfy the constructive interference condition, i.e.,
2μtcosr=(2n+1)/2
Only this wavelength λ would be present at that point with maximum intensity in the interference pattern in the reflected system. In the interference pattern, each fringe represents the locus of constant film thickness. In such a way, at different portions of the thin film, the reflected light must satisfy the above said condition so that we can observe colours in the interference pattern when thin film is illuminated with white light.
Example: Soap bubble: When white (sun) light is incident on a film of irregular thickness, say soap bubble, at all possible angles, there appears coloured fringes on the film. These fringes are due to interference of light reflected from the two surfaces of the thin film. The interference pattern is produced at a certain place on the soap bubble when its thickness and the angle of incidence of light satisfies the condition of constructive interference for certain wavelength of light. Hence, a soap bubble at that portion would appear with maximum intensity corresponding to that particular wavelength present in the white light. And this happens for each colour in white light. In such away, colours appear on a soap bubble when sunlight is incident on it.
Newton’s Rings are the circular interference pattern first discovered by physicist Sir Isaac Newton in 1704. It is cosists of concentric bright and dark rings with the point of contact of lens and the glass plate as centre,
The fringes obtained by interference of light waves by using the following arrangement
When a Plano convex lens with large radius of curvature is placed on a plane glass plate such that its curved surface faces the glass plate, a wedge air film (of gradually increasing thickness) is formed between the lens and the glass plate. The thickness of the air film is zero at the point of contact and gradually increases away from the point of contact.
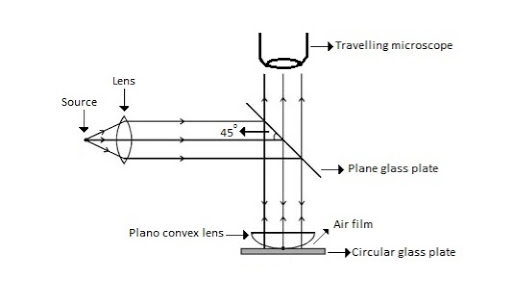
Figure 11: Newton Ring Assembly
If monochromatic (means light with single wavelength) light is allowed to fall normally on the lens from a source 'S', then two reflected rays R1 (reflected from upper surface of the film) and R2 (reflected from lower surface of the air film) interfere to produce circular interference pattern. This interference pattern has concentric alternate bright and dark rings around the point of contact. This pattern is observed through traveling microscope.
MATHEMATICAL ANALYSIS OF NEWTON’S RING
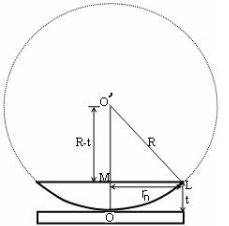
Figure 12
(OL)2 =(O’M)2-(ML)2 ……….(1)
R2=(R-t)2 +rn2
R2=R2 +t2-2Rt +rn2
Radius is large as compared to the thickness
So t2 is neglected as t2<< R2
R2=R2 +-2Rt +rn2
2Rt =rn2
Thickness of the film t =rn2 /2R ……….(2)
THEORY OF FRINGES:
The effective path difference between the two reflected rays R1 and R2 for a wedge shaped film from equation
∆ = 2μtcos(r+θ) +λ/2 ……….(3)
If the light is incident normally on the lens,
r = 0 and near to point of contact θ is small;
Therefore near point of contact, (r+θ) approaches to 0 and cos(r+θ)=cos0=1
Therefore
∆ = 2μt+λ/2 ……….(4)
Also At point of contact t = 0 therefore the effective path difference ∆ = λ/2
Which is odd multiple of λ/2 Therefore the Central fringe is dark.
BRIGHT FRINGE : CONDITION OF MAXIMA
For the condition of maxima the effective path difference
∆ = ±nλ
Using equation (4) ∆ = 2μt+λ/2 we have
2μt+λ/2= ±nλ
2μt = ± (2n-1)λ /2 ……….(5)
DIAMETER OF BRIGHT RINGS
We know by equation (2) t =rn2 /2R substitute in equation (5) we have
2μ (rn2 /2R) = ± (2n-1)λ /2
rn2 = ± (2n-1)λR /2μ
We know diameter D=2r and for nth fringe Dn=2rn
So we have Dn2=± 2(2n-1)λR /μ
Dn=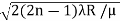
The medium enclosed between the lens and glass plate is if air therefore, 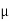 =1. The diameter of nth order bright fringe will be
=1. The diameter of nth order bright fringe will be
D=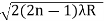 n=0,1,2,3,4……. ……….(6)
n=0,1,2,3,4……. ……….(6)
The diameter of bright ring is proportional to square root of odd natural numbers
DARK FRINGE : CONDITION FOR MINIMA
For the condition of minima, The effective path difference
∆ =± (2n+1)λ /2
2μt+λ/2 =± (2n+1)λ /2
2μt= ±nλ ……….(7)
It is clear that for particular dark or bright fringe t should be constant.
Every fringe is the locus of points having equal thickness. Hence the fringes are circular in shape.
DIAMETER OF DARK RINGS
We know by equation (2) t =rn2 /2R substitute in equation (7) we have
2μ (rn2 /2R ) = nλ
rn2 = nλR/ μ
We know diameter D=2r and for nth fringe Dn=2rn
So we have Dn2= 4nλR/ μ
Dn= 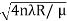
The medium enclosed between the lens and glass plate is if air therefore, 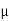 =1. The diameter of nth order bright fringe will be
=1. The diameter of nth order bright fringe will be
Dn= 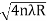 n=0,1,2,3,4……. ……….(8)
n=0,1,2,3,4……. ……….(8)
The diameter of dark ring is proportional to square root of natural numbers.
SPACING BETWEEN FRINGES
The Newton’s rings are not equally spaced because the diameter of ring does not increase in the same proportion as the order of ring and rings get closer and closer as ‘n’ increases.
For example the diameter of dark ring is given by Dn= 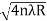 where n=0,1,2,3,4…….
where n=0,1,2,3,4…….
D3 - D2 =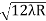 -
- 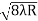 = (
= (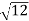 -
-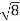 )
)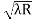 = 0.635
= 0.635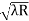
D7 – D6 =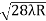 -
- 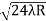 = (
= (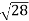 -
-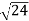 )
)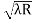 = 0.392
= 0.392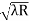
D10– D9 =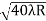 -
- 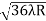 = (
= (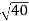 -
-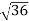 )
)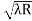 = 0.324
= 0.324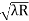
From above result we conclude that the fringe width reduces with increase in n.
APPLICATION OF NEWTON’S RING
- Determination of Wavelength of Light
The diameter of the nth order ring is calculated by subtracting the left and right side position of the microscope. As we know that the square of diameter of nth dark ring is
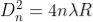
Therefore the square of diameter of (n+p)th ring is
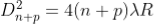
Subtracting both the above equation
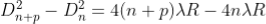 ………...(9)
………...(9)
Therefore
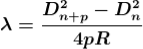 .............(10)
.............(10)
2. Determination of Refractive Index of liquid
In order to determine the refractive index of liquid the Newton’s ring experiment is first performed for the air medium and the difference in the square of the diameter of (n+p)th and nth dark ring is found as discussed above.
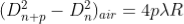 ………….(11)
………….(11)
After this few drops of liquid of μ refractive index is placed on the glass plate. The plano-convex lens is then placed on the glass plate, as a result a film of liquid is formed between the lens and the plate.
The difference in the square of the diameter of (n+p)th and nth dark ring is again calculated in the same manner for the liquid medium.
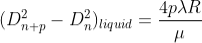 …..….(12)
…..….(12)
Dividing equation 2.29 by 2.30, we get
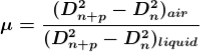 …….….(13)
…….….(13)
3. Newton’s ring with white light
If the monochromatic source is replaced by the white light, dark and bright fringes are not produced. Because the diameter of the rings depends upon wavelength and it is proportional to the square root of wavelength.
If If the monochromatic source is replaced by the white light superposition of rings take place due to different wavelength. Few coloured rings are seen around dark centre later illumination is seen in the field of view. As shown in below figure.

Figure 13
Example: In a Newton’s rings experiment the diameter of the 15th ring was found to be 0.59 cm and that of the 5th ring is 0.336 cm. If the radius of curvature of the lens is 100 cm, find the wave length of the light.
Solution:
The given data are
Diameter of Newton’s 15th ring (D15) = 0.59 cm = 0.59×10–2 m
Diameter of Newton’s 5th ring (D5) = 0.336 cm = 0.336 × 10–2 m
Radius of curvature of lens (R) = 100 cm = 1 m
Wave length of light (λ) = ?
Here m is difference between rings = 15-5=10
λ = D2n+m - D2n / 4mR
λ = (0.59×10–2 )2- (0.336 × 10–2)2 / 4 x 10 x 1
λ = 0.3481 x10-4 – 0.112896 x10-4 / 40
λ =0.00588 x 10-4 m
λ =5880 x 10-10 m
λ =5880Å
Diffraction
When the light falls on the obstacle whose size is comparable with the wavelength of light then the light bends around the obstacle and enters in the geometrical shadow. This bending of light is called diffraction.
FRAUNHOFFER DIFFRACTION AT SINGLE SLIT
The adjacent figure represents a narrow slit AB of width ‘e’. Let a plane wavefront of monochromatic light of wavelength '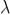 ' is incident on the slit. Let the diffracted light be focused by means of a convex lens on a screen. According to Huygen Fresnel, every point of the wavefront in the plane of the slit is a source of secondary wavelets. The secondary wavelets traveling normally to the slit i.e., along OP0 are brought to focus at -+
' is incident on the slit. Let the diffracted light be focused by means of a convex lens on a screen. According to Huygen Fresnel, every point of the wavefront in the plane of the slit is a source of secondary wavelets. The secondary wavelets traveling normally to the slit i.e., along OP0 are brought to focus at -+
AzP0 by the lens. Thus P0 is a bright central image. The secondary wavelets traveling at an angle '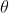 ' are focused at a point P1 on the screen.
' are focused at a point P1 on the screen.
The intensity at the point P1 is either minimum or maximum and depends upon the path difference between the secondary waves originating from the corresponding points of the wavefront.
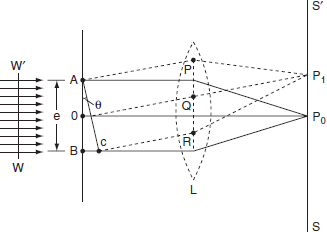
Figure 14
Theory:
In order to find out the intensity at P1, draw a perpendicular AC on BR.
The path difference between secondary wavelets from A and B in direction θ is BC i.e,
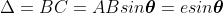
So, the phase difference,
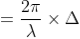
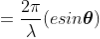
Let us consider that the width of the slit is divided into ‘n’ equal parts and the amplitude of the wave from each part is ‘a’.
So, the phase difference between two consecutive points
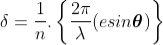 ........... (1)
........... (1)
Then the resultant amplitude R is calculated by using the method of vector addition of amplitudes
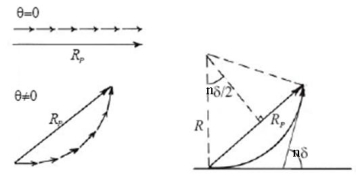
Figure 15
The resultant amplitude of n number of waves having same amplitude 'a' and having common phase difference of ' ' is
' is
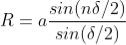 ................... (2)
................... (2)
Substituting the value of 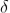 in equation (2)
in equation (2)
R = a 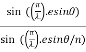 ................... (3)
................... (3)
Substituting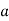 =
=  .esinθ in equation (3)
.esinθ in equation (3)
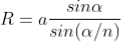
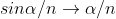
As  is small value; sin
is small value; sin 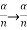
R = n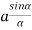
And na = A
Therefore
R =A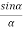 ................... (4)
................... (4)
Therefore, the Intensity is given by
I =R2 = A2 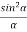 ................... (5)
................... (5)
Case (i): Principal Maximum:
Eqn (4) takes maximum value for
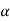 = 0
= 0
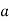 =
=  .esinθ = 0
.esinθ = 0
Sinθ = 0 or θ=0
The condition
The condition θ=0 means that this maximum is formed by the secondary wavelets which travel normally to the slit along OP0 and focus at P0. This maximum is known as “Principal maximum”.
Intensity of Principal maxima
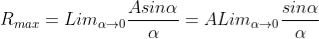
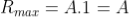
Therefore
Imax = R2max = A2
Case (ii): Minimum Intensity positions:
Equation (3) takes minimum values for sin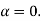 The values of '
The values of '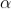 ' which satisfy sin
' which satisfy sin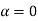 are
are
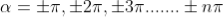
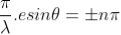
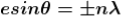 where
where 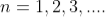 ………...(6)
………...(6)
In the above equation (6) n = 0 is not applicable because corresponds to principal maximum. Therefore, the positions according to equation (6) are on either side of the principal maximum.
Case (iii): Secondary maximum:
In addition to principal maximum at 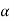 = 0, there are weak secondary maxima between minima positions. The positions of these weak secondary maxima can be obtained with the rule of finding maxima and minima of a given function in calculus. So, differentiating equation (5) and equating to zero, we have
= 0, there are weak secondary maxima between minima positions. The positions of these weak secondary maxima can be obtained with the rule of finding maxima and minima of a given function in calculus. So, differentiating equation (5) and equating to zero, we have
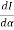 =
= 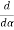 (A2
(A2 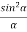 ) =0
) =0
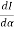 = 2A2
= 2A2 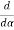 (
( 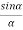 )(
)(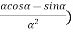 =0
=0
A2 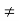 0;
0; 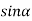 =0
=0
Because 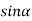 =0 correspond to minima positions
=0 correspond to minima positions
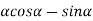 =0
=0
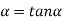 ………... (7)
………... (7)
The values of '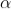 ' satisfying the equation (7) are obtained graphically by plotting the curves
' satisfying the equation (7) are obtained graphically by plotting the curves 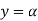 and
and 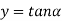 on the same graph.
on the same graph.
The points of intersection of the two curves gives the values of 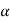 which satisfy equation (7).
which satisfy equation (7).
The points of intersections are
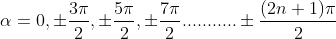
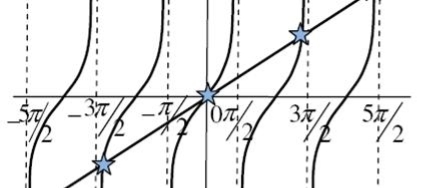
Figure 16
But 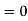 , gives principal maximum, substituting the values of
, gives principal maximum, substituting the values of 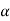 in equation (5), we get
in equation (5), we get
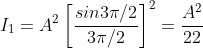
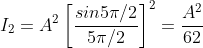
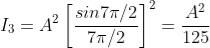
And so on.
From the above expressions, Imax, I1, I2,I3… it is evident that most of the incident light is concentrated at the principal maximum.
INTENSITY DISTRIBUTION GRAPH
A graph showing the variation of intensity with '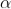 ' is as shown in the adjacent figure
' is as shown in the adjacent figure
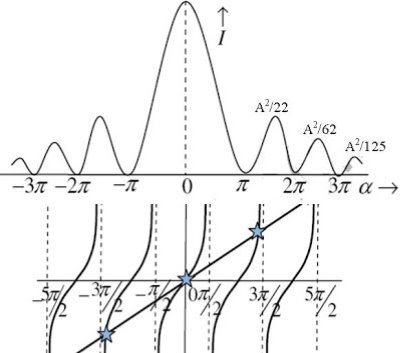
Figure 17
The double slits have been represented as A1B1 and A2B2 in Figure the slits are narrow and rectangular in shape. The planes of the slits are perpendicular to plane of the paper. Let the width of both the slits be equal and it is ‘e’ and they are separated by opaque length ‘d’. A monochromatic plane wave front of wave length ‘λ’ is incident normally on both the slits.
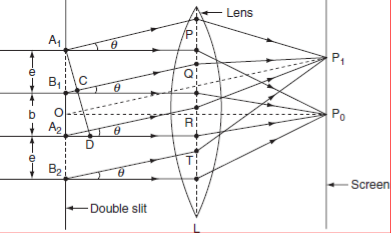
Figure 18
THEORY:
Light is made incident on arrangement of double slit. The secondary wavelets travelling in the direction of OP0 are brought to focus at P0 on the screen SS′ by using a converging lens L. P0 corresponds to the position of the central bright maximum. The intensity distribution on the screen is the combined effect of interference of diffracted secondary waves from the slits.
The diffracted intensity on the screen is very large along the direction of incident beam [i.e along OP0]. Hence it is maximum at P0. This is known as principal maximum of zero order.
The intensity at point P1 on the screen is obtained by applying the Fraunhofer diffraction theory at single slit and interference of diffracted waves from the two slits. The diffracted wave amplitude due to single slit at an angle θ with respect to incident beam is A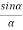 , where 2α is the phase difference between the secondary wavelets arising at the end points of a slit.
, where 2α is the phase difference between the secondary wavelets arising at the end points of a slit.
This phase difference can be estimated as follows: Draw a normal from A1 to B1Q. Now, B1C is the path difference between the diffracted waves at an angle ‘θ’ at the slit A1B1.
From the triangle A1B1C
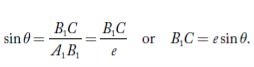
The corresponding phase difference
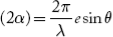
Or 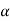 =
= 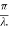 .esinθ …………(1)
.esinθ …………(1)
The diffracted wave amplitudes, 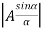 at the two slits combine to produce interference. The path difference between the rays coming from corresponding points in the slits A1B1 and A2B2 can be found by drawing a normal from A1 to A2R. A2D is the path difference between the waves from corresponding points of the slits.
at the two slits combine to produce interference. The path difference between the rays coming from corresponding points in the slits A1B1 and A2B2 can be found by drawing a normal from A1 to A2R. A2D is the path difference between the waves from corresponding points of the slits.
In the triangle
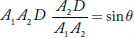
Or the path difference A2D = A1A2 sin θ = (e + b) sin θ
The corresponding phase difference
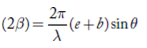 …………(2)
…………(2)
Applying the theory of interference on the wave amplitudes 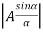 at the two slits gives the resultant wave amplitude (R).
at the two slits gives the resultant wave amplitude (R).
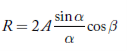 …………(3)
…………(3)
The intensity at P1 is
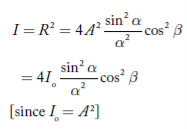 …………(4)
…………(4)
Equation (4) represents the intensity distribution on the screen. The intensity at any point on the screen depends on α and β. The intensity of central maximum is 4Io. The intensity distribution at different points on the screen can be explained in terms of path difference between the incident and diffracted rays as follows.
In equation (4) the term cos2β corresponds to interference and 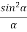 corresponds to diffraction. Now, we will shall look at the conditions for interference and diffraction maxima and minima.
corresponds to diffraction. Now, we will shall look at the conditions for interference and diffraction maxima and minima.
INTERFERENCE MAXIMA AND MINIMA:
If the path difference A2D = (e + b) sinθn = ± nλ where n = 1, 2, 3… then ‘θn’ gives the directions of the maxima due to interference of light waves coming from the two slits. The ± sign indicates maxima on both sides with respect to the central maximum.
On the other hand if the path difference is odd multiples of λ/2 i.e.,
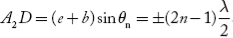
Then θn gives the directions of minima due to interference of the secondary waves from the two slits on both sides with respect to central maximum.
Diffraction maxima and minima:
If the path difference B1C = e sinθn = ± nλ, where n = 1, 2, 3… then θn gives the directions of diffraction minima. The ± sign indicates minima on both sides with respect to central maximum.
For diffraction maxima
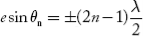
Is the condition. The ± sign indicates maxima on both sides with respect to central maximum.
The intensity distribution on the screen due to double slit diffraction is shown in Figure.
Figure(a) represents the graph for interference term,
Figure (b) shows the graph for diffraction term and
Figure (c) represents the resultant distribution.
Based on the relative values of e and b certain orders of interference maxima are missing in the resultant pattern.
The direction of interference maxima are given as (e + b) sin θn = nλ where n = 1, 2, 3, ….. And the directions of diffraction minima are given as e sin θm = mλ where m = 1, 2, 3, …
Figure: Intensity distribution due to diffraction at double slit.
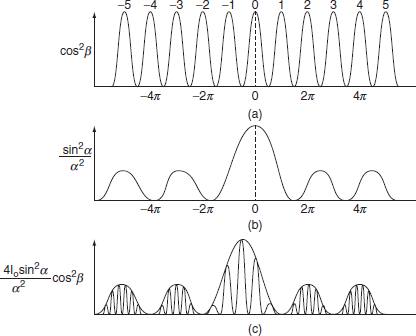
Figure 19
For some values of θn, the values of e and b are satisfied such that at these positions the interference maxima and the diffraction minima are formed. The combined effect results in missing of certain orders of interference maxima. Now we see certain values of e and b for which interference maxima are missing.
(i) Let e = b
Then, 2esinθn = nλ and esinθm = mλ
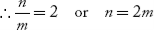
If m = 1, 2, 3 … then n = 2, 4, 6… i.e., the interference orders 2, 4, 6 … missed in the diffraction pattern
(ii) If 2e = b
Then 3e sin θm = nλ and e sin θm = mλ
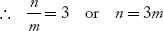
If μ = 1, 2, 3… Then n = 3, 6, 9… i.e the interference orders 3, 6, 9… are missed in the diffraction pattern
(iii) if e + b = e
i.e b = 0
The two slits are joined. So, the diffraction pattern is due to a single slit of width 2e.
An arrangement consisting of large number of parallel slits of the same width and separated by equal opaque spaces is known as Diffraction grating.
Gratings are constructed by ruling equidistant parallel lines on a transparent material such as glass, with a fine diamond point. The ruled lines are opaque to light while the space between any two lines is transparent to light and acts as a slit. This is known as plane transmission grating. When the spacing between the lines is of the order of the wavelength of light, then an appreciable deviation of the light is produced.
Theory: A section of a plane transmission grating AB placed perpendicular to the plane of the paper is as shown in the figure.
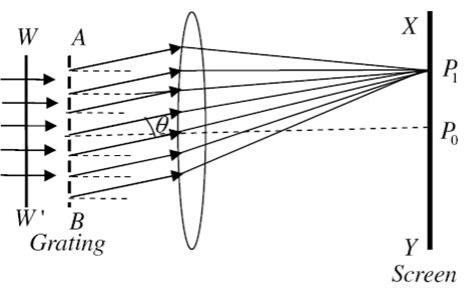
Figure 20
Let ‘e’ be the width of each slit and‘d’ the width of each opaque space. Then (e+d) is known as grating element and XY is the screen. Suppose a parallel beam of monochromatic light of wavelength 'λ' be incident normally on the grating. By Huygen’s principle, each of the slit sends secondary wavelets in all directions. Now, the secondary wavelets travelling in the direction of incident light will focus at a point Po on the screen. This point Po will be a central maximum.
Now consider the secondary waves travelling in a direction inclined at an angle 'θ' with the incident light will reach point P1 in different phases. As a result dark and bright bands on both sides of central maximum are obtained.
The intensity at point P1 may be considered by applying the theory of Fraunhofer diffraction at a single slit. The wavelets proceeding from all points in a slit along their direction are equivalent to a single wave of amplitude A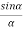 starting from the middle point of the slit,
starting from the middle point of the slit,
Where
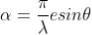
If there are N slits, then we have N diffracted waves. The path difference between two consecutive slits is (e+d)sin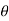 . Therefore, the phase difference
. Therefore, the phase difference
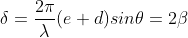 ........(1)
........(1)
Hence the intensity in a direction 'v ' can be found by finding the resultant amplitude of N vibrations each of amplitude A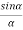 and a phase difference of '2
and a phase difference of '2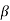 '
'
Since in the previous case
A = A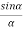 ; n=N;
; n=N; 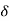 =2
=2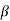
Substituting these in equation
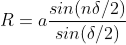
The resultant amplitude on screen at P1 becomes
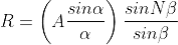 ..........(2)
..........(2)
Thus Intensity at P1 will be
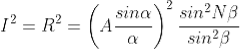 ........(3)
........(3)
The factor
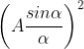
Gives the distribution of Intensity due to a single slit while the factor
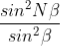
Gives the distribution of intensity as a combined effect of all the slits
Intensity Distribution:
Case (i): Principal maxima:
The equation (2) will take a maximum value if
Sin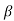 =0
=0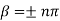 ; n =0,1,2,3………
; n =0,1,2,3………
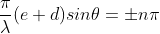
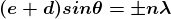 .......(4)
.......(4)
n = 0 corresponds to zero order maximum. For n = 1,2,3,… we obtain first, second, third,… principal maxima respectively. The ± sign indicates that there are two principal maxima of the same order lying on either side of zero order maximum.
Case(ii): Minima Positions:
The equation (2) takes minimum value if
Sin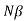 =0 but sin
=0 but sin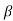
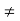 0
0 
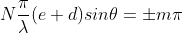
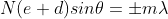 ...........(5)
...........(5)
Where m has all integral values except m = 0, N, 2N, …, nN, because for these values sin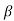 becomes zero and we get principal maxima. Thus, m = 1, 2, 3, …(N-1). Hence
becomes zero and we get principal maxima. Thus, m = 1, 2, 3, …(N-1). Hence
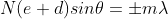
Where
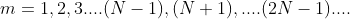
Gives the minima positions which are adjacent to the principal maxima.
Case(iii): Secondary maxima:
As there are (N-1) minima between two adjacent principal maxima there must be (N-2) other maxima between two principal maxima. These are known as secondary maxima. To find their positions
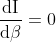
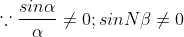
Only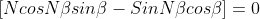
 ............(6)
............(6)
The roots of the above equation other than those for which 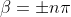 give the positions of secondary maxima The equation (6) can be written as
give the positions of secondary maxima The equation (6) can be written as
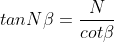
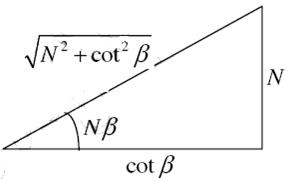
Figure 21
From the triangle we have
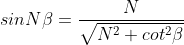
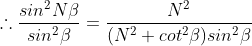
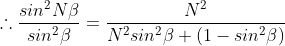
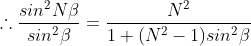
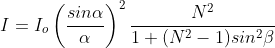
Since intensity of principal maxima is proportional to N2,
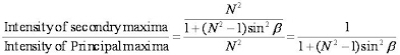
Hence if the value of N is larger, then the secondary maxima will be weaker and becomes negligible when N becomes infinity.
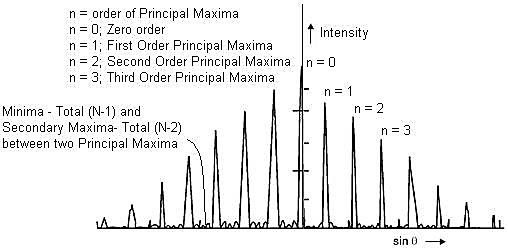
Figure 22
A set of large number of parallel slits of same width and separated by opaque spaces is known as diffraction grating.
Diffraction gratings are much more effective than prisms for dispersing light of different wavelengths so they are used almost exclusively in instruments designed to detect and identify characteristic spectral lines. There is nothing mysterious about these devices.
Fraunhofer used the first grating consisting of a large number of parallel wires placed side by side very closely at regular separation. Now the gratings are constructed by ruling the equidistance parallel lines on a transparent material such as glass with fine diamond point. The ruled lines are opaque to light while the space between the two lines is transparent to light and act as a slit.
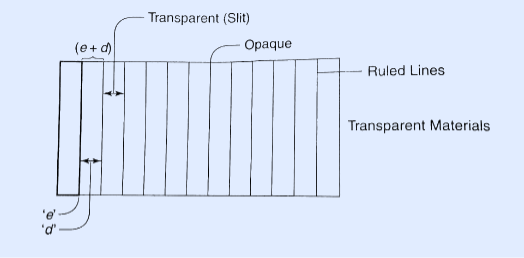
Figure 23
Let ‘e’ be the width of line and ‘d’ be the width of the slit.
Then (e + d) is known as grating element.
If N is the number of lines per inch on the grating then
(𝑒+𝑑)=1𝑖𝑐ℎ=2.54𝑐𝑚
(𝑒+𝑑)=2.54𝑐𝑚/𝑁
Commercial gratings are produced by taking the cost of actual grating on a transparent film like that of cellulose acetate. Solution of cellulose acetate is poured on a ruled surface and allowed to dry to form a thin film, detachable from the surface. This film of grating is kept between the two glass plates.
Example: A parallel beam of monochromatic light of wavelength 500nm is inclined normally on a plane diffraction grating 4000 per centimetre. Calculate the angle of diffraction for first order principal maximum.
Solution:
Given: number of lines per cm =4000
Grating element e+b = 1/4000 cm = 2.5 x 10-6m
λ=500 nm
Order n =1
(e+b) sinθ =nλ
Sinθ = nλ / (e+b)
Sinθ = 1 x 500 x 10-9 / 2.5 x 10-6
Sinθ =0.2
θ =sin-1 0.2
θ = 11.5o
Limit of Resolution:
The minimum distance between two points on the object so that their images (as produced by the optical instrument) are just seen as separate from each other is called limit of resolution of the optical instrument.
Statement: Two sources are resolvable by an optical instrument when the central maximum of one diffraction pattern falls over the first minimum of the other diffraction pattern and vice versa.
Let us consider the resolution of two wavelengths by a grating. When the difference in wavelengths is smaller and such that the central maximum of the wavelength coincides with the first minimum of the other as shown in figure, then the resultant intensity curve is as shown by the thick curve. The curve shows a distinct dip in the middle of two central maxima. Thus the two wavelengths can be distinguished from one another and according to Rayleigh they are said to be “Just Resolved”.
If the difference in wavelengths is such that their principal maxima are separately visible, then there is a distinct point of zero intensity in between the two wavelengths. Hence according to Rayleigh they are said to be “Resolved”.
When the difference in wavelengths is so small that the central maxima corresponding to two wavelengths come still closer as shown in figure, then the resultant intensity curve is quite smooth without any dip. This curve is as if there is only one wavelength somewhat bigger and stronger.
Hence according to Rayleigh the two wavelengths are “Not Resolved”.
Thus the two spectral lines can be resolved only up to a certain limit expressed by Rayleigh Criterion.
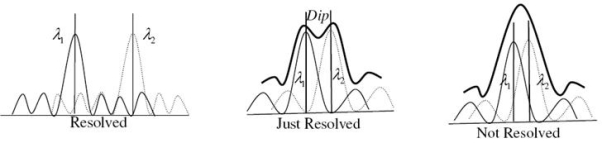
Figure 24
It may be possible that while the first order spectra is clearly visible, second order may be not be visible at all and the third order may again be visible.
This happens when for a given angle of diffraction θ, the path difference between the diffracted rays from the two extreme ends of one slit is equal to an integral multiple of λ.
Suppose the path difference is λ, then each slit can be considered to be made up of two halves, the path difference between the secondary waves from the corresponding points in the two halves will be λ / 2. Now they will cancel one another resulting zero intensity.
Thus the mining of single slit pattern are obtained in the direction given by.
Asinθ= mλ …………(1)
Where m = 1, 2, 3, excluding zero but the condition for nth order principles maximum in the grating spectrum is
(a + b) sinθ= nλ …………… (2)
If the two conditions given by equation (2) are simultaneously satisfied then the direction in which the grating spectrum should give us a maximum every slit by itself will produce darkness in that direction and hence the most favourable phase for reinforcement will not be able to produce an illumination i.e. The resultant intensity will be zero and hence the absent spectrum. Therefore dividing equation (2) by equation (1)
((a+ b) sinθ) /a sinθ=n/ m
(a+ b) /a =n/m
This is the condition for the absent spectra in the diffraction pattern
If a= b i.e., the width of transparent portion is equal to the width of opaque portion then from equation (3) n = 2m i.e., 2nd, 4th, 6th etc., orders of the spectra will be absent corresponds to the minima due to single slit given by m = 1, 2, 3 etc.
b = 2a …………..(3)
n=3m i.e., 3rd, 6th, 9th etc., order of the spectra will be absent corresponding to a minima due to a single slit given by m = 1, 2, 3 etc.
Dispersive power of a grating is defined as the ratio of the difference in the angle of diffraction of any two neighbouring spectral lines to the difference in the wavelength between the two spectral lines.
Or
It can also be defined as the diffraction in the angle of diffraction per unit change in wavelength.
The diffraction of the nth order principal maximum for a wavelength λ is given by the equation,
(a + b) sin θ = nλ (1)
Differentiating this equation with respect to θ and λ
a + b is constant and n is constant in a given order.
(a + b) cos θ dθ = n dλ
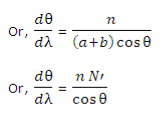 (2)
(2)
In equation (2) dθ/dλ is the dispersive power,
n is the order of the spectrum,
N’ is the number of lines per cm of the grating surface and
θ is the angle of diffraction for the nth order principal maximum of wavelength λ.
From equation (2), it is clear, that the dispersive power of the grating is directly proportional to the number of lines per cm and inversely proportional to cos θ.
Thus, the angular spacing of any two spectral lines is double in the second order spectrum in comparison to the first order. Secondly, the angular dispersion of the lines is more with a grating having larger number of lines per cm. Thirdly, the angular dispersion is minimum when θ = 0. If the value of θ is not large the value of cosθ can be taken as unity approximately and the influence of the factor cosθ in the equation (2) can be neglected.
Neglecting the influence of cosθ, it is clear that the angular dispersion of any two spectral lines (in a particular order) is directly proportional to the difference in wavelength between the two spectral lines. A spectrum of this type is called a normal spectrum.
If the linear spacing of two spectral lines of wavelength λ and λ + dλ is dx in the focal plane of the telescope objective or the photographic plate, then,
Dx = fdθ
Where ƒ is the focal length of the objective. The linear dispersion
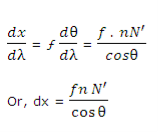
The linear dispersion is useful in studying the photographs of a spectrum.
It is defined as the capacity of a grating to form separate diffraction maxima of two wavelengths which are very close to each other
It is measured by λ/dλ where dλ is the smallest difference in two wavelengths which are just resolvable by grating and λ is the wavelength of either of them or mean wavelength.
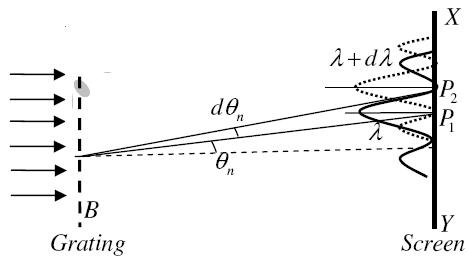
Figure 25
Let AB represent the surface of a plane transmission grating having grating element (e+d) and N total number of slits.
Let a beam of light having two wavelengths by λ and dλ is normally incident on the grating. Let P1 is nth primary maximum of a spectral line of wavelength λ at an angle of diffraction 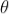 and P2 is the nth primary maximum of wavelength λ+dλ at diffracting angle θ+dθ.
and P2 is the nth primary maximum of wavelength λ+dλ at diffracting angle θ+dθ.
According to Rayleigh criterion, the two wavelengths will be resolved if the principal maximum λ+dλ of nth order in a direction θ+dθ falls over the first minimum of nth order in the same direction θ+dθ.
Let us consider the first minimum of l of nth order in the direction θ+dθ as below.
The principal maximum of  in the θ direction is given by
in the θ direction is given by
(e+d)sinθ =nλ ………………(1)
The equation of minima is
N(e+d)sinθ = mλ ………………(2)
Where m takes all integers except 0, N, 2N, …, nN, because for these values of m, the condition for maxima is satisfied.
Thus first minimum adjacent to nth principal maximum in the direction θ+dθ can be obtained by substituting the value of ‘m’ as (nN+1).
Therefore, the first minimum in the direction of θ+dθ is given by
N(e+d)sin(θ+dθ) = (nN+1)λ
(e+d)sin(θ+dθ) = (n+ )λ ………………(3)
)λ ………………(3)
The principal maximum of λ+dλ in direction θ+dθ is given by
(e+d)sin(θ+dθ) = n(λ+dλ) ………………(4)
Dividing eqn(3) by equation (4), we get
(n+ )λ = n(λ+dλ)
)λ = n(λ+dλ)
nλ + = nλ + ndλ
= nλ + ndλ
 = ndλ
= ndλ
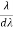 = nN
= nN
Resolving Power = 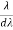 = nN ………………(5)
= nN ………………(5)
Thus the resolving power is directly proportional to
(i) The order of the spectrum ‘n’
(ii) The total number of lines on the grating ‘N
Example: A grating has 1100 lines ruled on it. What is difference between the two wavelengths that just appear resolved in the first order spectrum in the region of wavelength λ = 660 nm?
Solution:
N = 1100 nm
λ = 660 x 10-9 m
n = 1
R = λ /dλ =Nn
dλ = λ /Nn
dλ = 660 x 10-9 / 1100 x 10-9 x 1
dλ = 0.6 x 10-9 m
NUMERICAL PROBLEM
Example: A grating containing 4000 slits per centimetre is illuminated with a monochromatic light and produces the second-order bright line at a 30° angle. What is the wavelength of the light used? (1 Å = 10-10 m)
Solution:
The distance between slits (d) = 1 / (4000 slits / cm) = 0.00025 cm = 2.5 x 10-4 cm = 2.5 x 10-6 meters
Order (n) = 2
Sin 30o = 0.5
1 Å = 10-10 m
Wavelength of the light (λ) =?
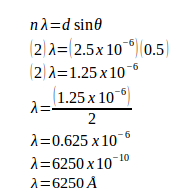
Example: A monochromatic light with a wavelength of 2.5x10-7 m strikes a grating containing 10,000 slits/cm. Determine the angular positions of the second-order bright line.
Solution:
Given
The distance between slits (d) = 1 / (10,000 slits / cm) = 0.0001 cm = 1 x 10-4 cm = 1 x 10-6 m
Order (n) = 2
Wavelength (λ) = 2.5 x 10-7 m
Angle (θ)
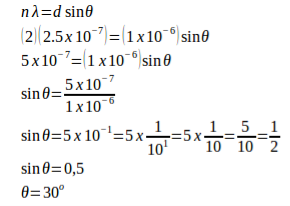
Example: A monochromatic light with wavelength of 500 nm (1 nm = 10-9 m) strikes a grating and produces the second-order bright line at an 30° angle. Determine the number of slits per centimetre.
Solution:
Wavelength (λ) = 500.10-9 m = 5.10-7 m
θ = 30o
n = 2
Distance between slits:
d sin θ = n λ
d (sin 30o) = (2)(5.10-7)
d (0.5) = 10.10-7
d = (10.10-7) / 0.5
d = 20.10-7
d = 2.10-6 m
Number of slits per centimetre:
x = 1 / d
x = 1 / 2.10-6 m
x = 0.5.106 / 1 m
x = 0.5.106 / 102 cm
x = 0.5.104 cm
x = 5.103 /cm
x = 5000 /cm
Example: A monochromatic light with wavelength of 500 nm (1 nano = 10-9) strikes a grating and produces the fourth-order bright line at an 30° angle. Determine the number of slits per centimetre.
Solution:
Wavelength (λ) = 500.10-9 m = 5.10-7 m
θ = 30o
n = 4
Distance between slits:
d sin θ = n λ
d (sin 30o) = (4)(5.10-7)
d (0.5) = 20.10-7
d = (20.10-7) / 0.5
d = 40.10-7
d = 4.10-6 m
Number of slits per centimetre:
x = 1 / 4.10-6 m
x = 0.25.106 / m
x = 0.25.106 / 102 cm
x = 0.25.104 / cm
x = 25.102 per cm
x = 2500 per cm