UNIT- 5
POLARIZATION& LASER
The phenomena of interference and diffraction confirm the wave nature of light hence neither of these phenomena is able to indentify the nature of waves that light is. These phenomena do not tell whether the oscillation of light waves are longitudinal or transverse in nature. This is accompalished by the study of polarization.
A light wave that is vibrating in more than one plane is referred to as unpolarized light.
Example: Light emitted by the sun, by a lamp in the classroom, or by a candle flame is unpolarized light.
These unpolarized light is created by electric charges that vibrate in a variety of directions, this concept of unpolarized light is difficult to visualize. For simplicity it is helpful to visualize unpolarized light as a wave that has an average of half its vibrations in a horizontal plane and half of its vibrations in a vertical plane. It is possible to transform unpolarized light into polarized light.
Polarized light waves are light waves in which the vibrations occur in a single plane. The process of transforming unpolarized light into polarized light is known as polarization.
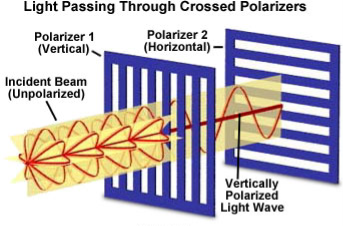
Figure 1
Classification of light
Light in the form of a plane wave in space is said to be linearly polarized. Light is a transverse electromagnetic wave, but natural light is generally unpolarized, all planes of propagation being equally probable. If light is composed of two plane waves of equal amplitude by differing in phase by 90°, then the light is said to be circularly polarized. If two plane waves of differing amplitude are related in phase by 90°, or if the relative phase is other than 90° then the light is said to be elliptically polarized.
Linearly Polarized: Light in the form of a plane wave in space is said to be linearly polarized. The electric field of light is limited to a single plane along the direction of propagation.
Circularly Polarized If light is composed of two plane waves of equal amplitude by differing in phase by 90°, then the light is said to be circularly polarized. If the thumb of your right hand were pointing in the direction of propagation of the light, the electric vector would be rotating in the direction of your fingers.
Elliptically Polarized If two plane waves of differing amplitude are related in phase by 90°, or if the relative phase is other than 90° then the light is said to be elliptically polarized. If the thumb of your right hand were pointing in the direction of propagation of the light, the electric vector would be rotating in the direction of your fingers.
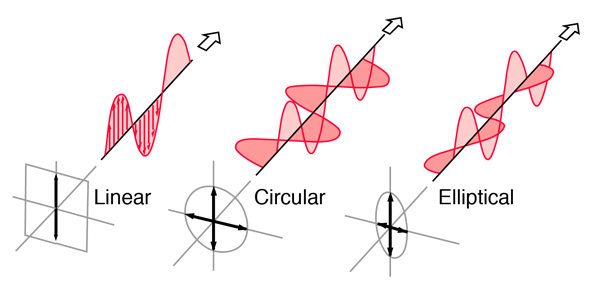
Figure 2: Showimg Linear, Circular and Elliptical Polarization
POLARIZATION BY REFLECTION
Production of Polarized Light by Reflection
The Brewster’s law can be used to polarise the light by reflection. When unpolarised light is incident on the boundary between two transparent media, the reflected light is polarised with its electric vector perpendicular to the plane of incidence when the refracted and reflected rays make a right angle with each other.
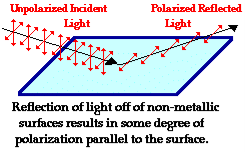
Figure 3
Thus we have seen that when reflected wave is perpendicular to the refracted wave, the reflected wave is a totally polarised wave. The electric field vectors of all unpolarized light may be resolved into two components as follows;
- Tangential component- in the plane of incidence.
- Normal components – in the plane perpendicular to plane of incidence.
The angle of incidence in this case is called Brewster’s angle
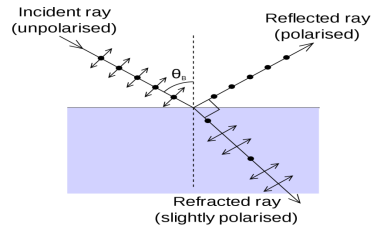
Figure 4
If the angle of incidence θi is varied, the reflected coefficient ‘r’ for the em waves corresponding to the tangential component will vary as shown in figure. As θi increases r will decrease.
At θi = Brewster angle (about 57° for glass) r will be zero and no reflection of the tangential component will take place.
The reflected beam will contain light waves having only the normal component for the electric field as shown in figure that is the reflected light will be plane polorized with the oscillations of electric field vector normal to the plane of incidence.
Cause of Polrizaton by Reflection
The em waves are generated because of the oscillation of electric charge. The electric field vectors of the transmitted ray act on the electrons in the dielectric.
Since the intensity of em wave emitted by the oscillating charge is maximum in a direction normal to the plane of oscillation, and zero along the line of oscillations for the plane polarized light having electric field vector in the plane of incidence, there will be no emition of em waves in a direction normal to the reflected ray. In figre the direction along which no emission should accur is called as zero intensity line. Let the angle between the reflected ray and the zero intensity line be 𝛿 the angle between the reflected and tranmitted ray is π/2 + 𝛿 suppose we arrange the angle of incidence such that
n=sinθi / sinθr
n=sinθi / sin(π/2 – θi)
n=sinθi / cosθi
n=tan θi
That is possible when
θi + θr = π/2 according to Brewster’s law
From figure
θi + θr+ π/2 + = π
As θi + θr = π/2
So π/2+ π/2 + = π
= 0
The line of zero intensity and the refected ray will coincide. Thuse there will be no reflection of light when the angle of incidence is equal to Brewster’s angle.
Thus the unpolarized light can be polarized by reflection as the reflected beam will contain light waves having electric field vector oscilating along normal to the plane of the incidence only.
PRODUCTION OF POLARIZED LIGHT BY REFRACTION
Polarization can also occur by the refraction of light. Refraction occurs when a beam of light passes from one material into another material. At the surface of the two materials, the path of the beam changes its direction. The refracted beam acquires some degree of polarization.
Birefringence, an optical property in which a single ray of unpolarized light entering an anisotropic medium is split into two rays, each traveling in a different direction. One ray (called the extraordinary ray) is bent, or refracted, at an angle as it travels through the medium; the other ray (called the ordinary ray) passes through the medium unchanged.
The ordinary ray and the extraordinary ray are polarized in planes vibrating at right angles to each other. The refractive index of the ordinary ray is constant in all directions; the refractive index of the extraordinary ray varies according to the direction because it has components that are both parallel and perpendicular to the crystal’s optic axis. An extraordinary ray can move either faster or slower than an ordinary ray.
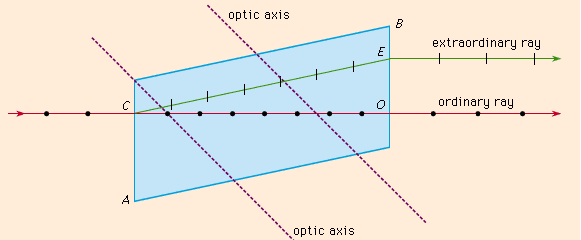
Figure 5
The Figure shows the phenomenon of double refraction through a calcite crystal. An incident ray is seen to split into the ordinary ray CO and the extraordinary ray CE upon entering the crystal face at C. If the incident ray enters the crystal along the direction of its optic axis, however, the light ray will not become divided.
The polarization occurs in a plane perpendicular to the surface. The polarization of refracted light is demonstrated by a unique crystal that serves as a double-refracting crystal.
Iceland Spar (calcite mineral), refracts incident light into two different paths. The light is split into two beams upon entering the crystal.
Figure 6
That mean if we see an object through an Iceland spar crystal, two images will observed. These two images are the result of the double refraction of light. Both refracted light beams are polarized - one in a direction parallel to the surface and the other in a direction perpendicular to the surface
Since these two refracted rays are polarized with a perpendicular orientation, a polarizing filter can be used to completely block one of the images. If the polarization axis of the filter is aligned perpendicular to the plane of polarized light, the light is completely blocked by the filter; meanwhile the second image is as bright as can be. And if the filter is then turned 90-degrees in either direction, the second image reappears and the first image disappears.
Negative and Positive Crystals:
Suppose vo and ve be the velocities of the ordinary and extraordinary rays. The crystals in which vo<ve are termed as negative and in which vo>ve are termed as positive. Calcite is negative crystal and quartz is an example of positive crystal.
Uniaxial and Biaxial crystals:
Uniaxial crystal: A crystal which has only one optic axis is called uniaxial crystal. The refractive index of the ordinary ray is constant for any direction in the crystal. Examples:- Calcite, Quartz, Ice, Tourmaline etc.
Biaxial crystal: A crystal which has only two optic axis is called biaxial crystal. The refractive index of the extraordinary ray is variable and depends on the direction. Examples:- Mica, Topaz, Borax etc.
All transparent crystals except those of the cubic system, which are normally optically isotropic, exhibit the phenomenon of double refraction: in addition to calcite, some well-known examples are ice, mica, quartz, sugar, and tourmaline. Other materials may become birefringent under special circumstances.
For example, solutions containing long-chain molecules exhibit double refraction when they flow; this phenomenon is called streaming birefringence. Some isotropic materials like glass may even exhibit birefringence when placed in a magnetic or electric field or when subjected to external stress.
DOUBLE REFRACTION BY NICOL PRISM
This was invented by William Nicol in the year 1828. Nicol prism is made from a double refracting calcite crystal.
A Nicol Prism is a type of polarizer, an optical device used to produce a polarized beam of light.
It is made in such a way that it eliminates one of the rays by total internal reflection, i.e. the ordinary ray is eliminated and only the extraordinary ray is transmitted through the prism.
Construction of Nicol prism:
- Length of calcite crystal is three times its breath.
- The corners A′G′ is blunt and A′C G′E is the principal section with ∠A′CG′ = 71°.
- The end faces A′BCD and EFG′H are grounded so that the angle ACG = 68°.
- The crystal is cut along the plane AKGL. The cut surfaces are polished until they are optically flat and cemented together with Canada balsam.
The refractive index of Canada balsam (1.55) is in between the refractive indices of ordinary (1.658) and extraordinary (1.486) rays in calcite crystal.
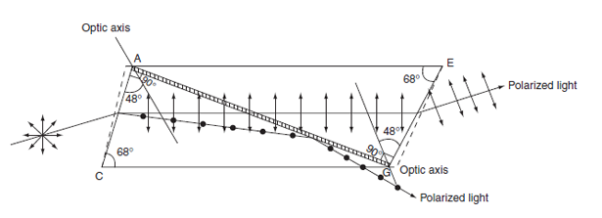Figure 7: Production of plane polarized light using Nicol prism
Working
- The diagonal AG represents the Canada balsam layer.
- A beam of unpolarized light is incident parallel to the lower edge on the face ABCD.
- The ray gets doubly refracted on entering into the crystal.
- From the refractive index values, we know that the Canada balsam acts as a rarer medium for the ordinary ray and it acts as a denser medium for extraordinary ray.
- When the angle of incidence for ordinary ray on the Canada balsam is greater than the critical angle then total internal reflection takes place, while the exaordinary ray gets transmitted through the prism.
- Nicol prism can be used as an analyser.
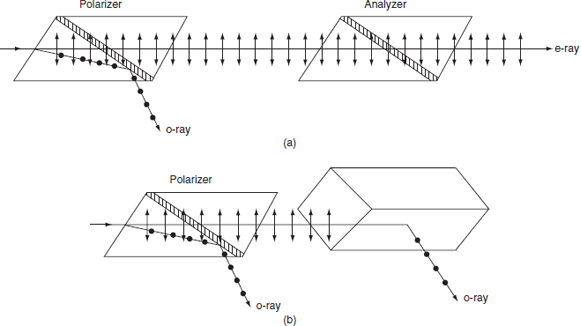
Figure 8: (a) Parallel Nicols; (b) Crossed Nicols
- Two nicol prisms are placed adjacently as shown in figure.
- One prism acts as a polarizer and the other act as an analyzer.
- The exaordinary ray passes through both the prisms.
- If the second prism is slowly rotated, then the intensity of the exaordinary ray decreases.
- When they are crossed, no light come out of the second prism because the e-ray that comes out from first prism will enter into the second prism and act as an ordinary ray. So, this light is reflected in the second prism. The first prism is the polarizer and the second one is the analyser.
POLARIZATION BY HALF WAVE AND QUARTER WAVE PLATE
A wave plate or retarder is an optical device that alters the polarization state of a light beam travelling through it. There are many types of retarders. Some common retarders are quarter-wave (λ/4) plates and half-wave(λ/2) plates.
A half-wave plate functions as a polarization rotator for linearly polarized light. It rotates the polarization of a linearly polarized light by twice the angle between its optic axis and the initial direction of polarization, as shown in Figure 22. It introduces a phase difference of radians between the
A typical wave plate is simply a birefringent crystal or a double refracting plastic foil with a carefully chosen thickness. If a beam of parallel light strikes perpendicularly a wave plate the light beam is splitted into two components due to its double refracting properties. The two components have planes of oscillation perpendicular to each other and slightly different phase velocities.
For a quarter-wave plate the thickness of the foil is chosen in such a manner that the light component whose electric field vector oscillates in parallel to the rotation lever lags by a λ/4 behind other perpendicular oscillating light component. For a half-wave plate the thickness is chosen so that the created phase difference has the amount of λ/2. In this experiment monochromatic light falls on a quarter-wave and half-wave plate. The polarization of the emergent light is investigated at different angles between the optic axis of the wave plates and the direction of the incident light.
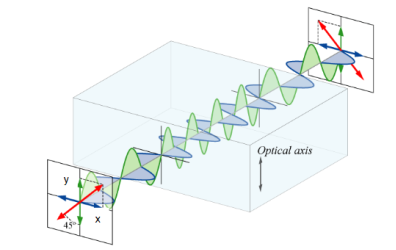
Figure 9
Half wave plate
A half-wave plate functions as a polarization rotator for linearly polarized light. It rotates the polarization of a linearly polarized light by twice the angle between its optic axis and the initial direction of polarization, as shown in Figure 22. It introduces a phase difference of radians between the two components of the electric field vectors.
Suppose a plane-polarized wave is normally incident on a wave plate, and the plane of polarization is at an angle ϕ with respect to the fast axis, as shown. After passing through the plate, the original plane wave has been rotated through an angle 2ϕ.
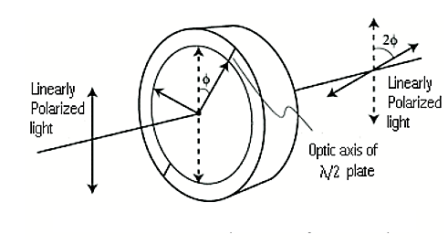
Figure 10
A half-wave plate is very handy in rotating the plane of polarization from a polarized laser to any other desired plane (especially if the laser is too large to rotate). Most large ion lasers are vertically polarized. To obtain horizontal polarization, simply place a half-wave plate in the beam with its fast (or slow) axis 45° to the vertical. The l/2 plates can also change left circularly polarized light into right circularly polarized light or vice versa. The thickness of half waveplate is such that the phase difference is 1/2 wavelength (l/2, Zero order) or certain multiple of 1/2-wavelength [(2n+1)l/2, multiple order].
Quarter Wave Plate
A quarter-wave plate is used to convert linear polarization to circular polarization and vice-versa. In order to obtain circular polarization, the amplitudes of the two E vector components must be equal and their phase difference must be 90 or 270 degrees. A quarter-wave plate is capable of introducing a phase difference of 90 degrees between the two components of incident light. However, this is not enough to produce circular polarization. The direction of polarization of the incident light with respect to the optic axis of the quarter-wave plate is equally important. It is obvious that the amplitudes of the two components will be equal only when the incident linear polarization direction makes an angle of 45 degrees with respect to the optic axis of the crystal(i.e.α= 45degrees). Figure 23 illustrates the conversion of linearly polarized light into circularly polarized light. Note that conversely, if circularly polarized light is incident on a quarter-wave plate, the resulting polarization will be linear, at an angle of 45 degrees with respect to the optic axis. Again, the reason is that a phase difference of 90 degrees is introduced between the two components of the electric field vector, which traces a helix-like path as the circularly polarized wave propagates.
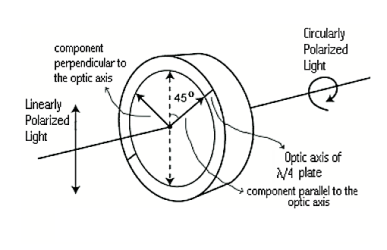
Figure 11
Optical Activity
Optical activity was first observed in quartz crystals in 1811 by a French physicist, François Arago. Louis Pasteur was the first to recognize that optical activity arises from the dissymmetric arrangement of atoms in the crystalline structures or in individual molecules of certain compounds.
Optical activity, the ability of a substance to rotate the plane of polarization of a beam of light that is passed through it. (In plane-polarized light, the vibrations of the electric field are confined to a single plane.
The intensity of optical activity is expressed in terms of a quantity, called specific rotation, defined by an equation that relates the angle through which the plane is rotated, the length of the light path through the sample, and the density of the sample (or its concentration if it is present in a solution). Because the specific rotation depends upon the temperature and upon the wavelength of the light, these quantities also must be specified. The rotation is assigned a positive value if it is clockwise with respect to an observer facing the light source, negative if counterclockwise. A substance with a positive specific rotation is described as dextrorotatory and denoted by the prefix d or (+); one with a negative specific rotation is levorotatory, designated by the prefix l or (-).
Optical activity is the ability of a chiral molecule to rotate the plane of plane-polairsed light, measured using a polarimeter. A simple polarimeter consists of a light source, polarising lens, sample tube and analysing lens.
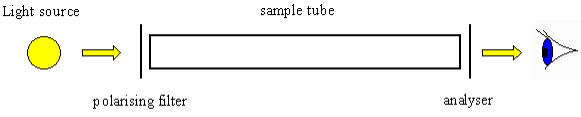
Figure 12
When light passes through a sample that can rotate plane polarised light, the light appears to dim because it no longer passes straight through the polarising filters. The amount of rotation is quantified as the number of degrees that the analysing lens must be rotated by so that it appears as if no dimming of the light has occurred.
Measuring Optical Activity
When rotation is quantified using a polarimeter it is known as an observed rotation, because rotation is affected by path length (l, the time the light travels through a sample) and concentration (c, how much of the sample is present that will rotate the light). When these effects are eliminated a standard for comparison of all molecules is obtained, the specific rotation, [a].
[a] = 100a / cl when concentration is expressed as g sample /100ml solution
Enantiomers will rotate the plane of polarisation in exactly equal amounts (same magnitude) but in opposite directions.
As already discussed Dextrorotary designated as d or (+), clockwise rotation (to the right) Levorotary designated as l or (-), anti-clockwise rotation (to the left).
If only one enantiomer is present a sample is considered to be optically pure. When a sample consists of a mixture of enantiomers, the effect of each enantiomer cancels out, molecule for molecule.
For example, a 50:50 mixture of two enantiomers or a racemic mixture will not rotate plane polarised light and is optically inactive. A mixture that contains one enantiomer excess, however, will display a net plane of polarisation in the direction characteristic of the enantiomer that is in excess.
Laurent’s half shade Polarimeter
Polarimeter – it is an optical instrument used to measure the angle of rotation of plane polarized light when it is passed through an optically active substance.
By measuring the angle, the specific rotation of an optically active substance can be determined.
Two types of polarimeters are generally used in the laboratory now a days Laurent’s Half Shade Polarimeter and Biquartz Polarimeter. We will discuss Laurent’s Half Shade Polarimeter.
Construction
- S is source of monochromatic light placed at the focus of convex
- Just after the convex lens there is a Nicol Prism P is placed. This prism acts as a polariser.
- H is a half shade device which divides the field of polarised light emerging out of the Nicol P into two halves generally of unequal brightness.
- T is a glass tube in which optically active solution is filled.
- The light after passing through T is allowed to fall on the analyzing Nicol A which can be rotated about the axis of the tube. (Don’t get confuse here, we already discussed in previous section that Nicol prism acts as a polariser as well as analyser).
- The rotation of analyser can be measured with the help of a scale.
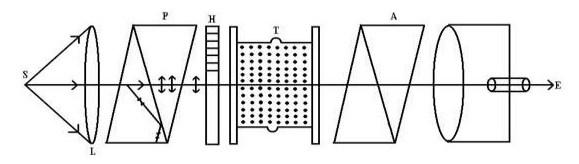
Figure 13
Laurent’s half shade polarimeter is shown in Figure 13
Working
To understand the working of this device we have to know the need of a Laurent half shade device. For this we assume that half shade device is not present.
In this basic setup (without the half-shade A) you are looking for the maximum and minimum brightness, which then tells you that the analyzer A is precisely aligned with the output rotation.
When tube is empty placed the analyzer in such a position that the view of field is completely dark. Note the position of the analyzer with the help of circular scale.
Now filled the tube with optically active solution and it is set in its proper position. The optically active solution rotates the plane of polarization of the light emerging out of the polariser P by some angle. So the light is transmitted by analyzer A and the field of view of telescope becomes bright.
Now the analyzer is rotated by a finite angle so that the field of view of telescope again become dark. This will happen only when the analyzer is rotated by the same angle by which plane of polarization of light is rotated by optically active solution.
The position of analyzer is again noted. The difference of the two readings will give you angle of rotation of plane of polarization.
But here the difficulty associated with this procedure that when analyzer is rotated for the total darkness, then it is attained gradually and hence it is difficult to find the exact position correctly for which complete darkness is obtained.
Figure 14
Laboratory Set Up of Poalrimeter
To overcome above difficulty half shade device is introduced between polariser P and glass tube T.
Half Shade Device
- It consist of two semi-circular plates ACB and ADC.
- One half ACB is made of glass while other half is made of quartz.
- Both the halves are joined together.
- The quartz is cut parallel to the optic axis.
- Thickness of the quartz is selected in such a way that it introduces a path difference of ‘A/2 between ordinary and extraordinary ray.
- The thickness of the glass is selected in such a way that it absorbs the same amount of light as is absorbed by quartz half.
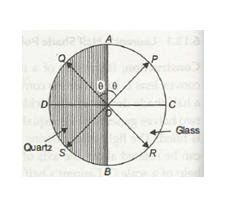
Figure 15
- Let us consider that the vibration of polarisation is along OP. On passing through the glass half the vibrations remain along OP. But on passing through quartz half these vibrations will split into o and e-components.
- The e-components are parallel to the optic axis while o-component is perpendicular to optic axis.
- The o-component travels faster in quartz and hence an emergence 0-component will be along OD instead of along OC.
- Thus components OA and OD will combine to form a resultant vibration along OQ which makes same angle with optic axis as OP.
Now if the Principal plane of the analysing Nicol is parallel to OP then the light will pass through glass half passable. Hence glass half will be brighter than quartz half or we can say that glass half will be bright and the quartz half will be dark. Similarly if principal plane of analysing. Nicol is parallel to OQ then quartz half will be bright and glass half will be dark.
When the principal plane of analyzer is along AOB then both halves will be equally bright. On the other hand if the principal plane of analyzer is along DOC. Then both the halves will be equally dark.
Thus it is clear that if the analysing Nicol is slightly disturbed from DOC then one half becomes brighter than the other. Hence by using half shade device, one can measure angle of rotation more accurately.
Mathematically
The specific rotation is given by S=θ/lC where l is length of tube and C is concentration.
Let us discuss Einstein’s theory of interaction of electromagnetic radiation with matter. He proposed that electromagnetic radiation interacts with matter in following three steps.
- Stimulated Absorption
- Spontaneous Emission
- Stimulated Emission
Stimulated Absorption:
Let E1 and E2 be the energies of ground and excited states of an atom. Suppose, if a photon of energy hν= E1− E2 interacts with an atom present in the ground state, the atom gets excitation form ground state E1 to excited state E2. This process is called stimulated absorption. Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons.
Stimulated absorption rate ∝ Number of atoms in the ground state
∝ Density of photons Spontaneous emission
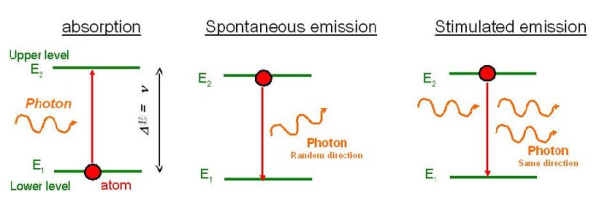
Figure 16
Spontaneous Emission:
Let E1 and E2 be the energies of ground and excited states of an atom. Suppose, if a photon of energy hν= E1− E2 interacts with an atom present in the ground state, the atom gets excitation form ground stateE1 to excited state E2. The excited atom does not stay in a long time in the excited state. The excited atom gets de-excitation after its life time by emitting a photon of energy hν= E1− E2. This process is called spontaneous emission. Also Spontaneous means by its own. Here excited atom comes to ground state by its own so it is named as spontaneous emission.
The spontaneous emission rate depends up on the number of atoms present in the excited state.
Spontaneous emission ∝ rate number of atoms in the excited state
Stimulated Emission:
This phenomena is responsible for producing laser light. Let E1and E2 be the energies of ground and excited states of an atom. Suppose, if a photon of energy hν= E1− E2 interacts with an atom present in the ground state, the atom gets excitation form ground stateE1 to excited state E2. Let, a photon of energy hν= E1− E2 interacts with the excited atom with in their life time; the atom gets de-excitation to ground state by emitting of another photon. These photons have same phase and it follows coherence. This phenomenon is called stimulated emission.
Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons.
Stimulated emission rate ∝ number of atoms in the excited state
∝ Density of photons
The distribution of atoms in the two energy levels will change by absorption or emission of radiation. Einstein introduced three empirical coefficients to quantify the change of population of the two levels. Let N1 be the number of atoms per unit volume with energy E1 and N2 be the number of atoms per unit volume with energy E2. Let ‘n’ be the number of photons per unit volume at frequency ‘υ’ such that hυ= E1− E2.
Then, the energy density of photons ρ(υ) = nhυ
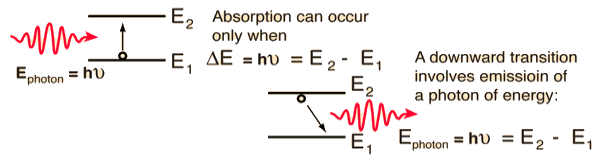
Figure:17
When these photons interact with atoms, both upward (absorption) and downward (emission) transition occurs.
At the equilibrium the upward transitions must be equal downward transitions.
Upward Transition
Stimulated absorption rate depends upon the number of atoms available in the lowest energy state as well as the energy density photons.
We have seen above that
Stimulated absorption rate ∝ N1 i.e. Number of atoms in the ground state
∝ ρ(υ) i.e. Density of photons spontaneous emission
Stimulated absorption rate = B12N1ρ(υ) ………(1)
Where B12 is the Einstein coefficient of stimulated absorption.
Downward transition
The spontaneous emission rate depends up on the number of atoms present in the excited state.
Spontaneous emission rate ∝ N2 i.e. number of atoms in the excited state
Spontaneous emission rate = A21N2 ………(2)
Where A21 is the Einstein coefficient of spontaneous emission.
Stimulated emission rate depends upon the number of atoms available in the excited state as well as the energy density of photons.
Stimulated emission rate ∝ N2 i.e. number of atoms in the excited state
∝ ρ(υ) i.e. Density of photons
Stimulated emission rate = B21N2ρ(υ) ………(3)
If the system is in equilibrium the upward transitions must be equal downward transitions.
Upward transitions = downward transitions
B12N1ρ(υ) = A21N2 + B21N2ρ(υ) ………(4)
B12N1ρ(υ) - B21N2ρ(υ) = A21N2
(B12N1- B21N2) ρ(υ) = A21N2
ρ(υ) =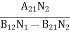
………(5)
Divide with B21N2 in numerator and denominator in right side of the above equation,
ρ(υ) =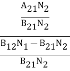 
= 
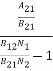………(6)
ρ(υ) =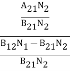 
= 
=
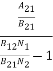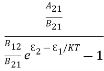………(7)
We know from Maxwell Boltzmann distribution law
= 
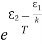………(8)
And also from Planck’s law, the radiation density
ρ(υ) =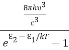 
………(9)
Comparing the two equations (7) and (9)
=
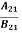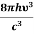and 
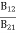=1 ………(10)
The above relations referred to as Einstein relations.
From the above equation for non degenerate energy levels the stimulated emission rate is equal to the stimulated absorption rate at the equilibrium condition.
= 
………(11)
Definition
The number of atoms present in the excited state or higher energy state is greater than the number of atoms present in the ground state or lower energy state is called population inversion.
Population inversion as name suggests that this is inverted phenomena. In general lower energy level is more populated that means it have more number of atoms in lower energy level as compared to higher energy level. But by pumping we will obtain a state when the number of atoms present in the higher energy state is greater than the number of atoms present in lower energy state.
Let us consider two level energy system of energies E1 and E2 as shown in figure.
Let N1 and N2 be the populations that means number of atoms per unit volume of energy levels E1 and E2 respectively.
According to Boltzmann’s distribution the population of an energy level E, at temperature T is given by
Ni=N0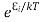 
Where N0 is the population of the lower level or ground state and k is the Boltzmann’s constant.
From the above relation, the population of energy levels E1 and E2 are
N1=N0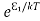 
N2=N0 
At ordinary conditions N1 >N2 i.e., the population in the ground or lower state is always greater than the population in the excited or higher states. The stage of making, population of higher energy level is greater than the population of lower energy level is called population inversion i.e. N1 < N2
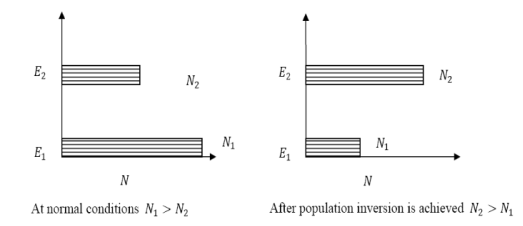
Figure 18
When population inversion method is used to enforce more and more atoms to give up photons. This initiates a chain reaction and releasing massive amount of energy.
This results in rapid build-up of energy of emitting one particular wavelength traveling coherently in fixed direction. This process is called amplification by stimulated emission using population inversion.
This population inversion situation is essential for a laser action. For any stimulated emission, It is necessary that the upper energy level or meta stable state should have a long life time, i.e., the atoms should pause at the meta stable state for more time than at the lower level.
Pumping mechanisms of population inversion
Thus for laser action, pumping mechanism (exciting with external source) maintain a higher population of atoms in the upper energy level relative to that in the lower level.
A system in which population inversion is achieved is called as an active system. The method of raising the particles from lower energy state to higher energy state is called pumping.
The process of achieving of population inversion is called pumping.
This can be done by number of ways.
The most commonly used pumping methods are
- Optical pumping
- Electrical discharge pumping
- Chemical pumping
- Thermal Pumping
- Injection current pumping
- Inelastic Atom-Atom Collisions
Optical pumping As the name suggests, in this method, light is used to supply energy to the laser medium. Optical pumping is used in solid laser. Xenon flash tubes are used for optical pumping. Since these materials have very broad band absorption, sufficient amount of energy is absorbed from the emission band of flash lamp and population inversion is created. So xenon flash lamp is used to produce more electrons in the higher energy level of the laser medium.
Examples of optically pumped lasers are ruby, Nd: YAG Laser(Neodymium: Yttrium Aluminum Garnet).
Electrical discharge pumping Electrical discharge pumping is used in gas lasers. Since gas lasers have very narrow absorption band pumping then any flash lamp is not possible. Electric discharge refers to flow of electrons or electric current through a gas, liquid or solid.
In this method of pumping, electric discharge acts as the pump source or energy source. A high voltage electric discharge (flow of electrons, electric charge, or electric current) is passed through the laser medium or gas. The intense electric field accelerates the electrons to high speeds and they collide with neutral atoms in the gas. As a result, the electrons in the lower energy state gains sufficient energy from external electrons and jumps into the higher energy state
Examples of Electrical discharge pumped lasers are He-Ne laser, CO2 laser, argon-ion laser etc.
Chemical pumping Chemical reaction may also result in excitation and hence creation of population inversion in few systems.
If an atom or a molecule is produced through some chemical reaction and remains in an excited state at the time of production, then it can be used for pumping. The hydrogen fluoride molecule is produced in an excited state when hydrogen and fluorine gas chemically combine. The number of produced excited atoms or molecules is greater than the number of normal state atoms or molecules. Thus, population inversion is achieved.
Examples H2 + F2 → 2HF, in this chemical reaction, hydrogen (H2) and fluorine (F2) molecules are chemically combined to produce hydrogen fluoride molecule (2HF) in an excited state.
Thermal Pumping: Sometimes we can achieve population inversion by heating the laser medium. In thermal pumping, heat acts as the pump source or energy source. In this method, population inversion is achieved by supplying heat into the laser medium.
When heat energy is supplied to the laser medium, the lower energy state electrons gains sufficient energy and jumps into the higher energy level.
The process of achieving population inversion in thermal pumping is almost similar to the optical pumping or electric discharge method, except that in this method heat is used as pump source instead of light or electric discharge.
Injection current pumping In semiconductors, injection of current through the junction results in creates of population inversion among the minority charge carriers.
Examples of such systems are InP and GaAs.
Inelastic Atom-Atom Collisions: Like the electric discharge method, here also a high voltage electric discharge acts as a pump source. However, in this method, a combination of two types of gases, say X and Y are used. The excited state of gas X is represented as X+ whereas gas Y is represented as Y+. Both X and Y gases have the same excited states (X+ and Y+).
When high voltage electric discharge passes through a laser medium having two types of gases X and Y, the lower energy state electrons in gas X will move to the excited state X+ similarly the lower energy state electrons in gas Y moves to the excited state Y+.
Initially, during electric discharge, the lower energy state electrons in gas X or atom X gets excited to X+ due to continuous collision with electrons. The excited state electrons in gas X+ now collide with the lower energy state electrons in gas Y. As a result, the lower energy state electrons in gas Y gains sufficient energy and jump into the excited state Y+. This method is used in the Helium–Neon (He-Ne) laser.
- Two-level laser
- Three-level laser
- Four-level laser
TWO-LEVEL LASER
Consider a group of electrons with two energy levels E1 and E2.
E1 is the lower energy state and E2 is the higher energy state.
N1 is the number of electrons in the energy state E1.
N2 is the number of electrons in the energy state E2.
The number of electrons per unit volume in an energy state is the population of that energy state.
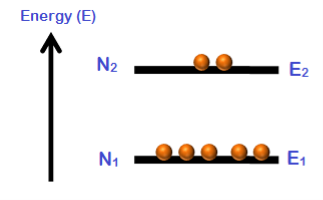
Figure 19
Population inversion cannot be achieved in a two energy level system. Under normal conditions, the number of electrons (N1) in the lower energy state (E1) is always greater as compared to the number of electrons (N2) in the higher energy state (E2).
N1 > N2
When temperature increases, the population of higher energy state (N2) also increases. However, the population of higher energy state (N2) will never exceeds the population of lower energy state (N1).
At best an equal population of the two states can be achieved which results in no optical gain.
N1 = N2
Two energy level lasers are not possible. We can not get population inversion in a 2 level LASER no matter how much we pump the atoms in the ground state. And since population inversion is a necessity for lasing action, we don't have two level lasers.
Therefore, we need 3 or more energy states to achieve population inversion. The greater is the number of energy states the greater is the optical gain.
There are certain substances in which the electrons once excited; they remain in the higher energy level or excited state for longer period. Such systems are called active systems or active media which are generally mixture of different elements.
When such mixtures are formed, their electronic energy levels are modified and some of them acquire special properties. Such types of materials are used to form 3-level laser or 4-level laser.
THREE-LEVEL LASER
The two energy levels between which lasing occur are: the lower laser energy level (E1), and the upper laser energy level (E2).
To simplify the explanation, we neglect spontaneous emission.
To achieve lasing, energy must be pumped into the system to create population inversion. So, that more atoms will be in energy level E2 than in the ground level (E1).
Atoms are pumped from the ground state (E1) to energy level E3. They stay there for an average time of 10-8 [sec], and decay (usually with a non-radiative transition) to the meta-stable energy level E2.
A schematic energy level diagram of a laser with three energy levels is shown in figure,
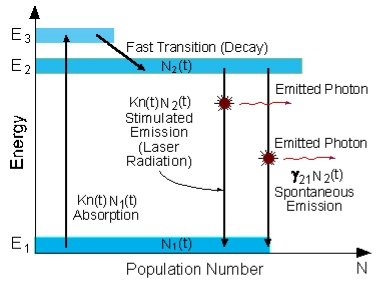
Figure 20: Energy level diagram in a three level laser
Since the lifetime of the meta-stable energy level (E2) is relatively long (of the order of 10-3 [sec], many atoms remain in this level.
If the pumping is strong enough, then after pumping more than 50% of the atoms will be in energy level E2, a population inversion exists, and lasing can occur.
In a three-level system, the laser transition ends on the ground state. The unpumped gain medium exhibits strong absorption on the laser transition. A population inversion and consequently net laser gain result only when more than half of the ions (or atoms) are pumped into the upper laser level; the threshold pump power is thus fairly high.
The population inversion can be achieved only by pumping into a higher-lying level, followed by a rapid radiative or non-radiative transfer into the upper laser level, because in this way one avoids stimulated emission caused by the pump wave. (For transitions between only two levels, simultaneous pump absorption and signal amplification cannot occur.)
An example of a three-level laser medium is ruby (Cr3+:Al203), as used by Maiman for the first laser.
FOUR -LEVEL LASER
As seen in Figur, there is four energy levels, with energies E1, E2, E3, E4 with populations of N1, N2, N3, N4 respectively. There energies increase for each level so that E1 < E2 < E3 < E4.
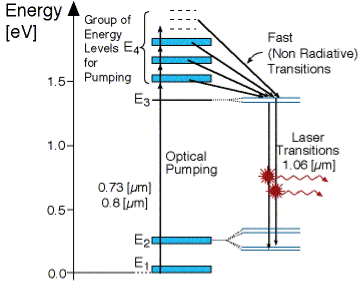
Figure 21
In this system, optical pumping from the ground state (E1 ) into the pump band (E4) excites the atoms. From this level the atoms decay by a fast, radiationless transition into the level 3 (E3). The lifetime of the laser transition from E3 – E2 is long compared to that of E4 –E3, a population accumulates in this level 3 (lasing level).
Here the atoms relax and start to create laser transitions through spontaneous and stimulated emissions into level 2 (E2). At this level, like level 4 has a fast decay into the ground state. Like before this quickly de-excited atom leads to a negligible population in E2.
This is significant, as the highly populated E3 level will then form a population inversion with the E2 level. Specifically as long as the population of level 3 N3 is greater then 0. Therefore optical amplification and laser operation can take place.
Since only a small number of atoms need to be excited in the upper lasing level E3 to form population inversion, it proves that a 4 level laser is much more efficient and practical then the 3 level laser.
A lower threshold pump power can be achieved with a four-level laser medium, where the lower laser level is well above the ground state and is quickly depopulated e.g. By multi-phonon transitions. Ideally, no appreciable population density in the lower laser level can occur even during laser operation. In that way, reabsorption of the laser radiation is avoided (provided that there is no absorption on other transitions). This means that there is no absorption of the gain medium in the unpumped state, and the gain usually rises linearly with the absorbed pump power.
The most popular four-level solid-state gain medium is Nd:YAG. All lasers based on neodymium-doped gain media, except those operated on the ground-state transition around 0.9-0.95 pm, are four-level lasers.
Neodymium ions can also be directly pumped into the upper laser level, e.g. With pump light around 880 nm for Nd:YAG. Even though effectively only three levels are involved, the term three-level system would not be used here.
Ruby laser is a three level solid state laser and was constructed by Maiman in 1960. Ruby laser is one of the few solid-state lasers that produce visible light. It emits deep red light of wavelength 694.3 nm.
Construction
A ruby laser consists of three important elements: laser medium, the pump source and the optical resonator.
Laser Medium
Ruby (Al2O3+Cr2O3) is a crystal of Aluminium oxide, in which 0.05% of Al+3 ions are replaced by the Cr+3 ions. The colour of the rod is pink. The active medium or laser medium in the ruby rod is Cr+3 ions. In ruby laser 4cm length and 5mm diameter rod is generally used. The ruby has good thermal properties.
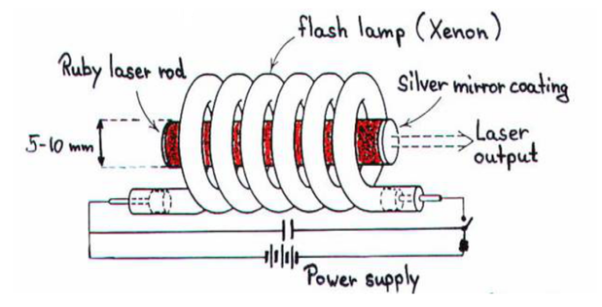
Figure 22
The pump source
The ruby rod is surrounded by xenon flash tube, which provides the pumping light to excite the chromium ions in to upper energy levels. The ruby rod was surrounded by a helical xenon flash lamp.
We know that population inversion is required to achieve laser emission. Population inversion is the process of achieving the greater population of higher energy state than the lower energy state. In order to achieve population inversion, we need to supply energy to the laser medium i.e. to ruby crystal.
Xenon flash tube emits thousands joules of energy in few milliseconds, but only a part of that energy is utilized by the chromium ions while the rest energy heats up the apparatus. A cooling arrangement is provided to keep the experimental set up at normal temperatures.
Optical resonator
Both the ends of the rods are highly polished and made strictly parallel. The ends are silvered in such a way, one becomes partially reflected the laser beam was emitted through that end and the other end fully reflected to reflect all the rays of light striking it.
Working of ruby laser:
Consider a ruby laser medium consisting of three energy levels E1, E2, E3 with N number of electrons.
We assume that the energy levels will be E1 < E2 < E3. The energy level E1 is known as ground state or lower energy state, the energy level E2 is known as metastable state, and the energy level E3 is known as pump state.
Let us assume that initially most of the electrons are in the lower energy state (E1) and only a tiny number of electrons are in the excited states (E2 and E3).
The energy level diagram of chromium ions is shown in figure. The chromium ions get excitation into higher energy levels by absorbing of 5500Å of wavelength radiation. The excited chromium ions stay in the level E3 for short interval of time (10-8 to 10-9 Sec). After their life time most of the chromium ions are de-excited from E3 to E1 and a few chromium ions are de-excited from E3 to E2.
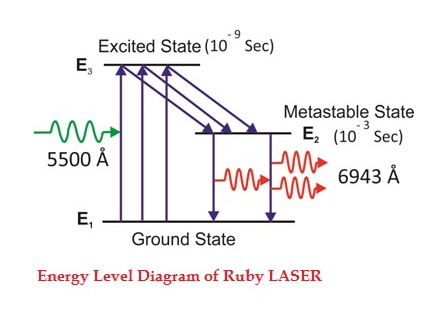
Figure 23
The transition between E3 and E2 is non-radioactive transition i.e. the chromium ions gives their energy to the lattice in the form of heat. In the Meta stable state the life time of chromium ions is 10-3 sec. The life time of chromium ions in the Meta stable state is 105 times greater than the life time of chromium ions in higher state.
Due to the continuous working of flash lamp, the chromium ions are excited to higher state E3 and returned to E2 level. After few milliseconds the level E2 is more populated than the level E1 and hence the desired population inversion is achieved. The state of population inversion is not a stable one. The process of spontaneous transition is very high. When the excited chromium ion passes spontaneously from E3 to E2it emits one photon of wave length 6943 Å. The photon reflects back and forth by the silver ends and until it stimulates an excited chromium ion in E2 state and it to emit fresh photon in phase with the earlier photon. The process is repeated again and again until the laser beam intensity is reached to a sufficient value. When the photon beam becomes sufficient intense, it emerges through the partially silvered end of the rod. The wave length 6943 Å is in the red region of the visible spectrum.
Draw backs of ruby laser
- The laser requires high pumping power
- The efficiency of ruby laser is very small
- It is a pulse laser
Application of ruby laser
- Ruby lasers are in optical photography
- Ruby lasers can be used for measurement of plasma properties such as electron density and temperature.
- Ruby lasers are used to remove the melanin of the skin.
- Ruby laser can be used for recording of holograms.
The first He-Ne gas laser was fabricated in 1961 by Ali Javan, Bennett and Herriott at Bell Telephone Laboratories. others. Helium-Neon laser is a type of gas laser in which a mixture of helium and neon gas is used as a gain medium. Helium-Neon laser is also known as He-Ne laser. The helium-neon laser was the first continuous wave laser ever constructed. The helium-neon laser operates at a wavelength of 632.8 nanometres (nm), in the red portion of the visible spectrum.
Ruby laser is a pulse laser, even it have high intense output. For continuous laser beam gas lasers are used. Using gas lasers, we can achieve highly coherence, high directionality and high monochromacity beam. The output power of the gas laser is generally in few milliwatts.
CONSTRUCTION
The helium-neon laser consists of three essential components:
- Pump source (high voltage power supply)
- Gain medium (laser glass tube or discharge glass tube)
- Resonating cavity
Pump source
The gain medium of a helium-neon laser is made up of the mixture of helium and neon gas contained in a glass tube at low pressure. In He-Ne gas laser, the He and Ne gases are taken in the ratio 10:1 in the discharge tube.
Gain medium
In He-Ne laser 80cm length and 1cm diameter discharge is generally used. The out power of these lasers depends on the length of the discharge tube and pressure of the gas mixture. Therefore, in order to achieve population inversion, we need to pump electrons from lower energy state of the helium. In He-Ne laser, neon atoms are the active centres and have energy levels suitable for laser transitions while helium atoms help in exciting neon atoms.
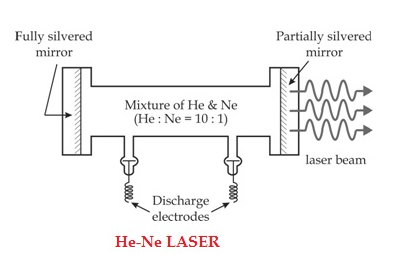
Figure 24
Resonating cavity
Two reflecting mirrors are fixed on either ends of the discharge tube, in that, one is partially reflecting and the other is fully reflecting. The fully silvered mirror will completely reflect the light whereas the partially silvered mirror will reflect most part of the light but allows some part of the light to produce the laser beam.
WORKING
When the electric discharge is passing through the gas mixture, the electrons accelerated towards the positive electrode. During their passage, they collide with He atoms and excite them into higher levels. 23s1 and 21s0 form ground state of He atom. In higher levels 23s1 and 21s0, the life time of He atoms is more. So there is a maximum possibility of energy transfer between He and Ne atoms through atomic collisions. When He atoms present in the levels 23s1 and 21s0 collide with Ne atoms present ground state, the Ne atoms gets excitation into higher levels 4s and 5s.
Due to the continuous excitation of Ne atoms, we can achieve the population inversion between the higher levels 4s and 5s and lower levels 3p and 4p. The various transitions 5s to 4p, 4s to 3p and 5s to 3p leads to the emission of wavelengths 3.93μm, 1.51μm and 6328 Å or 632.8μm.
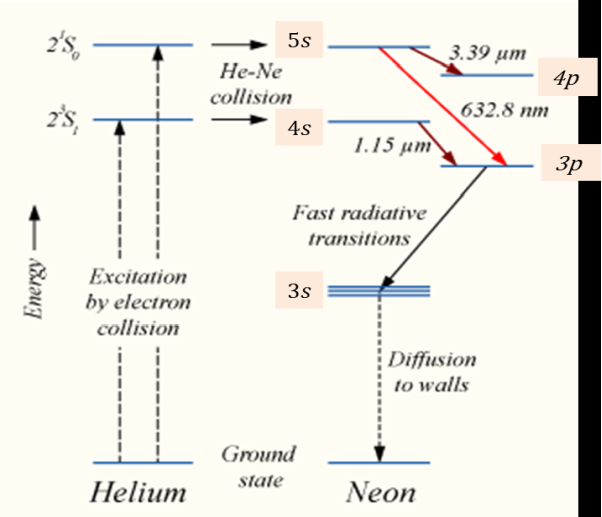
Figure 25
The first two corresponding to the infrared region while the last wavelength is corresponding to the visible region. The Ne atoms present in the 4s level are de-excited into 3s level, by spontaneously emitting a photon of around wavelength 6000 Å. When a narrow discharge tube is used, the Ne atoms present in the level 3s collide with the walls of the tube and get de-excited to ground state energy level.
ADVANTAGES OF HELIUM-NEON LASER
- Helium-neon laser emits laser light in the visible portion of the spectrum.
- High stability
- Low cost
- Operates without damage at higher temperatures
DISADVANTAGES OF HELIUM-NEON LASER
- Low efficiency
- Low gain
- Helium-neon lasers are limited to low power tasks
APPLICATIONS OF HELIUM-NEON LASERS
- Helium-neon lasers are used in industries.
- Helium-neon lasers are used in scientific instruments.
Helium-neon lasers are used in the college laboratories
Applications of lasers because of unique property of laser beam such as coherence, monochromacity, directionality, and high intensity, they are widely used in various fields like
1. Communication
2. Computers
3. Chemistry
4. Photography
5. Industry
6. Medicine
7. Military
8. Scientific Research
1. Communication
In case of optical communication semiconductors laser diodes are used as optical sources and its band width is (1014Hz) is very high compared to the radio and microwave communications. More channels can be sent simultaneously Signal cannot be tapped as the band width is large, more data can be sent. A laser is highly directional and less divergence, hence it has greater potential use in space crafts and submarine. It is used in optical fiber communications to send information over large distances with low loss. Laser light is used in underwater communication networks. Lasers are used in space communication, radars and satellites.
2. Computers
In LAN (local area network), data can be transferred from memory storage of one computer to other computer using laser for short time. Lasers are used in CD-ROMS during recording and reading the data. Lasers are used in computer printers.
3. Chemistry
Lasers are used in molecular structure identification Lasers are also used to accelerate some chemical reactions. Using lasers, new chemical compounds can be created by breaking bonds between atoms are molecules.
4. Photography
Lasers can be used to get 3-D lens less photography. Lasers are also used in the construction of holograms.
5. Industry
Lasers can be used to blast holes in diamonds and hard steel. Lasers are also used as a source of intense heat Carbon dioxide laser is used for cutting drilling of metals and non-metals, such as ceramics plastics glass etc. High power lasers are used to weld or melt any material. Lasers are also used to cut teeth in saws and test the quality of fabric. It is used to cut glass and quartz, used in electronic industries for trimming the components of Integrated Circuits (ICs).Lasers are used for heat treatment in the automotive industry. Laser light is used to collect the information about the prefixed prices of various products in shops and business establishments from the bar code printed on the product. Ultraviolet lasers are used in the semiconductor industries for photolithography. Photolithography is the method used for manufacturing printed circuit board (PCB) and microprocessor by using ultraviolet light. It is also used to drill aerosol nozzles and control orifices within the required precision.
6. Medicine
Pulsed neodymium laser is employed in the treatment of liver cancer. Argon and carbon dioxide lasers are used in the treat men of liver and lungs. Lasers used in the treatment of Glaucoma.
Lasers used in endoscopy to scan the inner parts of the stomach. Lasers used in the elimination of moles and tumors which are developing in the skin tissue and hair removal. It is also used for bloodless surgery.
Lasers are used to destroy kidney stones, in cancer diagnosis and therapy also used for eye lens curvature corrections. Lasers are used to study the internal structure of microorganisms and cells. It is used to create plasma. Lasers are used to remove the caries or decayed portion of the teeth.
7. Military
Lasers can be used as a war weapon. High energy lasers are used to destroy the enemy air-crofts and missiles. Lasers can be used in the detection and ranging likes RADAR. Laser range finders are used to determine the distance to an object. The ring laser gyroscope is used for sensing and measuring very small angle of rotation of the moving objects.
Lasers can be used as a secretive illuminators for reconnaissance during night with high precision.
8. Scientific research
Lasers are used in the field of 3D-photography Lasers used in Recording and reconstruction of hologram. Lasers are employed to create plasma. Lasers are used in Raman spectroscopy to identify the structure of the molecule and to count the number of atoms in a substance. Lasers are used in the Michelson- Morley experiment. A laser beam is used to confirm Doppler shifts in frequency for moving objects. A laser helps in studying the Brownian motion of particles. With the help of a helium-neon laser, it was proved that the velocity of light is same in all directions. Lasers are used to measure the pollutant gases and other contaminants of the atmosphere. Lasers help in determining the rate of rotation of the earth accurately. Lasers are used for detecting earthquakes and underwater nuclear blasts. A gallium arsenide diode laser can be used to setup an invisible fence to protect an area.
