UNIT I
Basic Concepts of Thermodynamics
Macroscopic Approach
Consider a certain amount of gas in a cylindrical container. The volume (V) can be measured by measuring the diameter and the height of the cylinder. The pressure (P) of the gas can be measured by a pressure gauge. The temperature (T) of the gas can be measured using a thermometer. The state of the gas can be specified by the measured P, V and T. The values of these variables are space averaged characteristics of the properties of the gas under consideration. In classical thermodynamics we often use this macroscopic approach. The macroscopic approach has the following features.
- The structure of the matter is not considered.
- A few variables are used to describe the state of the matter under consideration.
- The values of these variables are measurable following the available techniques of experimental physics.
Microscopic Approach
On the other hand, the gas can be considered as assemblage of a large number of particles each of which moves randomly with independent velocity. The state of each particle can be specified in terms of position coordinates (xi , yi , zi ) and the momentum components ( pxi , pyi , pzi ). If we consider a gas occupying a volume of 1 cm3 at ambient temperature and pressure, the number of particles present in it is of the order of 1020. The same number of position coordinates and momentum components are needed to specify the state of the gas. The microscopic approach can be summarized as:
- Knowledge of the molecular structure of matter under consideration is essential.
- A large number of variables are needed for a complete specification of the state of the matter
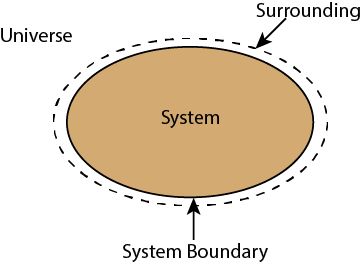
Whenever a change is to be analysed it is essential to specify the region in which the change take place. This is done by drawing a boundary around the region. Boundary may be real or imaginary.
Everything within the boundary is called the system. The region outside the boundary is called surroundings
There are three types of Thermodynamics systems:

1 – Open system (control volume system): If mass and energy both cross the boundary of a system it is called open system .in open system both mass and energy can transfer across the boundaries and the mass within the system may not be constant .most of the engineering devices are open systems involving flow of fluids through them.
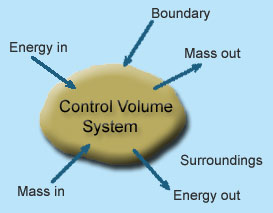
Example of open system
- Boiler – In boiler water convert from liquid to vapour phase. So mass and energy both transfer the boundary.
- Hydraulic turbine wheel – In this device potential energy of water convert into mechanical works. Water enters the wheel from head race side and leaves it to the tail race from the other end, and as such mass cross the system boundary.
- Motor-car engine – The engine sucks charge which is mixture of air and petrol and finally exhausts the gases to the surrounding atmosphere.
2 – Closed system (control mass system): If the mass within the boundary of the system does not change, it is called closed system. A closed system does not allow any mass transfer across the boundary but allow transfer of energy across the boundary.
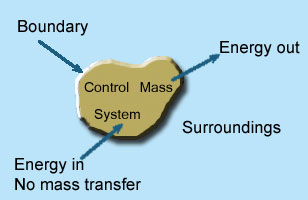
Example of closed system
- Piston cylinder assembly –the gas can reject or receive heat, expand or contract but no mass cross the boundary of system.
- Ignition system – electric energy cross the boundary to cause a spark between electrodes an initiate combustion .there is heat transfer but not mass across the system.
Pressure cooker, refrigerator, ice cream freezer etc. are the example of closed system.
3 - Isolated system : Neither mass nor energy cross the boundary of a system .it is called an isolated system . In this no mass and energy cross the system
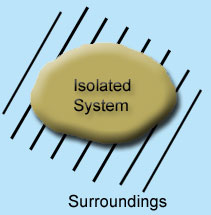
Example of isolated system
- Universe can be considered as an isolated system
- Fluid enclosed in a perfectly insulated closed vessel (thermos flask)
Intensive property: If the property is independent of mass of the system is called an intensive property.
Example - Pressure, temperature, density, velocity, height, viscosity are the example of intensive property.
Extensive property: If the property is proportional to the mass of the system it is called an extensive property.
Example- volume, surface area, potential energy, kinetic energy, internal energy, electric charge.
A system is said to be in the states of thermodynamics equilibrium if the value of the property is the same at all the points in the system. Or the system is said to exist in thermodynamics equilibrium when no change in any macroscopic property is registered, if the system is isolated from its surrounding.
The system is said to be in thermodynamic equilibrium if the conditions for following three equilibrium is satisfied:
- Mechanical equilibrium
- Chemical equilibrium
- Thermal equilibrium
1-Mechanical equilibrium: When there are no unbalanced forces within the system and between the system and the surrounding, the system is said to be under mechanical equilibrium.
The system is also said to be in mechanical equilibrium when the pressure throughout the system and between the system and surrounding is same. Whenever some unbalance forces exist within the system, they will get neutralized to attain the condition of equilibrium. Two systems are said to be in mechanical equilibrium with each other when their pressures are same.
2-Chemical equilibrium: The system is said to be in chemical equilibrium when there are no chemical reactions going on within the system or there is no transfer of matter from one part of the system to other due to diffusion. Two systems are said to be in chemical equilibrium with each other when their chemical potentials are same.
3-Thermal equilibrium: When the system is in mechanical and chemical equilibrium and there is no spontaneous change in any of its properties, the system is said to be in thermal equilibrium. When the temperature of the system is uniform and not changing throughout the system and also in the surroundings, the system is said to be thermal equilibrium. Two systems are said to be thermal equilibrium with each other if their temperatures are same.
States is the conditions of system identified by thermodynamics properties .the state of the system in thermodynamics equilibrium can be represented by a point with properties as coordinate’s .the system exist at a definite state when all the properties have a definite value.
The application of thermodynamic principles begins by defining a system that is in some sense distinct from its surroundings. For example, the system could be a sample of gas inside a cylinder with a movable piston, an entire steam engine, a marathon runner, the planet Earth, a neutron star, a black hole, or even the entire universe. In general, systems are free to exchange heat, work, and other forms of energy with their surroundings.
A system’s condition at any given time is called its thermodynamic state. For a gas in a cylinder with a movable piston, the state of the system is identified by the temperature, pressure, and volume of the gas. These properties are characteristic parameters that have definite values at each state and are independent of the way in which the system arrived at that state. In other words, any change in value of a property depends only on the initial and final states of the system, not on the path followed by the system from one state to another. Such properties are called state functions. In contrast, the work done as the piston moves and the gas expands and the heat the gas absorbs from its surroundings depends on the detailed way in which the expansion occurs.
The behaviour of a complex thermodynamic system, such as Earth’s atmosphere, can be understood by first applying the principles of states and properties to its component part in this case, water, water vapour, and the various gases making up the atmosphere. By isolating samples of material whose states and properties can be controlled and manipulated, properties and their interrelations can be studied as the system changes from state to state.
Thermodynamics process represents a transition in which a system changes from one state to another. When the path is completely specified then the change of state is called a process. A Process is defined as the transformation of the system from one fixed state to another fixed state .When any one of the properties changes, the working substance or system is said to have undergone a process.
Some of the processes are identified by special names as given below:
- Isobaric process (constant pressure process.
- Isochoric process (constant volume process)
- Isothermal process (constant temperature process)
- Isentropic process (constant entropy process)
- Adiabatic process(perfectly insulated process)
Cycle: Any process or series of processes whose end state are identical is called a cycle. Or Series of thermodynamic processes, the end states of which are identical, is called a thermodynamic cycle. In a thermodynamic cycle, chemical composition of the working fluid during the process does not change. Thus all the properties in the initial and final states remain unchanged.
Example - water that circulates through the steam power plant. There is a change of phase during the process, but the end states are same.
Heat: Heat is that form of energy for which the driving force is temperature difference. It is also defines as the heat is energy transferred across the boundary of a system because of a temperature difference between the system and surrounding. Heat is transient quantity which exists only as it crosses the boundary of a system.
Heat flowing into a system is considered positive while heat flowing out of a system is considered negative.
Work: In thermodynamics, work performed by a system is the energy transferred by the system to its surroundings. Kinetic energy, potential energy and internal energy are forms of energy that are properties of a system. Work is a form of energy, but it is energy in transit. A system contains no work, work is a process done by or on a system. In general, work is defined for mechanical systems as the action of a force on an object through a distance.
Work done by a system on its surrounding is considered positive while work done on the system by the surroundings is considered negative .
We know that
Work = force x displacement
But in case of thermodynamics works we take force is the product of a pressure p at the boundary and the area A of the moving boundary therefore
DW = pAdl
Where dW is the work done during an infinite displacement dl of the boundary.
Since Adl = dv = change in volume
DW = pdv
The conditions under which the above expression is valid are
- The system is closed
- There are no viscous effects within the system.
- The pressure and other properties have the same value on all boundaries of the system
- The effects due to gravity electricity or magnetism are negligible
If two systems are each in thermal equilibrium with the third system then the two system are in thermal equilibrium which each other.
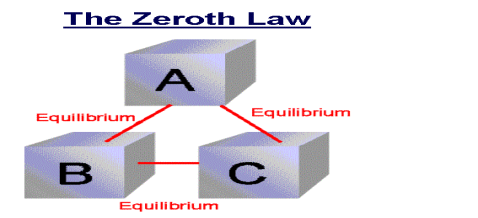
When a body A is in thermal equilibrium with a body B , and also separately with a body C ,then B and C will thermal equilibrium with each other .this is known as the Zeroth law of thermodynamics
Sometimes our body start to sweat and feel warm when we are in a room full of people and the sweating becomes excessive if the room size is small. This happens because our body is trying to cool off hence heat transfers from our body in the form of ‘sweat’. This entails the first law of thermodynamics.
The first law of thermodynamics states that the total energy of an isolated system is constant. Energy can be transformed from one form to another, but can neither be created nor destroyed.
According to this law, some of the heat given to system is used to change the internal energy while the rest in doing work by the system. Mathematically,
ΔQ=ΔU+ΔW
Where,
ΔQ = Heat supplied to the system
ΔW= Work done by the system.
ΔU = Change in the internal energy of the system.
If Q is positive, then there is a net heat transfer into the system, if W is positive, then there is work done by the system. So positive Q adds energy to the system and positive W takes energy from the system.
It can also be represented as ΔU=ΔQ−W
We can say that internal energy tends to increase when heat is given to the system and vice versa.
Limitations of First Law of Thermodynamics
- The limitation of the first law of thermodynamics is that it does not say anything about the direction of flow of heat.
- It does not say anything whether the process is a spontaneous process or not.
- The reverse process is not possible. In actual practice, the heat doesn’t convert completely into work. If it would have been possible to convert the whole heat into work, then we could drive ships across the ocean by extracting heat from the water of the ocean.
The first law of thermodynamics can be applied to a system to evaluate the changes in its energy when it undergoes a change of state while interacting with its surroundings. The processes that are usually encountered in thermodynamic analysis of systems can be identified as any one or a combination of the following elementary processes:
- Constant volume (isochoric) process
- Constant pressure (isobaric) process
- Constant temperature (isothermal) process.
- Adiabatic process.
Constant volume process: Suppose a gas enclosed in a rigid vessel is interacting with the surroundings and absorbs energy Q as heat. Since the vessel is rigid, the work done W due to expansion or compression is zero. Applying the first law, we get
DU = dQ or Q = U2 –U1
That is, heat interaction is equal to the change in internal energy of the gas. If the system contains a mass m equal of an ideal gas, then
Q = ΔU = mCv (T2 –T1)
The path followed by the gas is shown on a P-V diagram. Now consider the fluid contained in a rigid vessel as shown. The vessel is rigid and insulated. Shaft work is done on the system by a paddle wheel as shown in Fig. a. In Fig. b electric work is done on the system. Since the vessel is rigid, the PdV work is zero. Moreover, the vessel is insulated and hence dQ = 0. Application of the first law of thermodynamics gives
DU = dQ – dW = dQ – (dWpdv + dWs)
Or dU = -dWs or – Ws = ΔU = U2 –U1
Where dWpdv is the compression /expansion work and dWs is the shaft work. That is increase in internal energy of a system at a constant volume, which is enclosed by an adiabatic wall, is equal to the shaft work done on the system.
Constant pressure process: Several industrial processes are carried out at constant pressure. A few examples of constant pressure processes are: (a) reversible heating/cooling of a gas (b) phase change (c) paddle wheel work (d) electrical work. For a constant pressure process, the work done W is given by
W = ∫PdV = P (V2-V1)
Application of the first law of thermodynamics gives
DU = dQ – dW = dQ – PdV = dQ – d (PV)
Or dQ = dU + d (PV) = d (U + PV) = dH
Or Q = ΔH
That is in a constant pressure process, the heat interaction is equal to the increase in the enthalpy of the system. Now consider the constant pressure processes in which the system is enclosed by an adiabatic boundary. Application of the first law gives:
DU = dQ – dW = dQ – (PdV + dWs)
Here, the net work done (dW) consists of two parts – the PdV work associated with the motion of the boundary and (-dWs), the shaft work (or electrical work) done by the surroundings. Since the system is enclosed by an adiabatic boundary, dQ = 0 the equation can be written as
-dWs = dU + d(PV) = dH
That is, the increase in the enthalpy of the system is equal to the shaft work done on the system.
Constant temperature process: Suppose a gas enclosed in the piston cylinder assembly is allowed to expand from P1 to P2 while the temperature is held constant. Then application of the first law gives:
DU = dQ – dW = dQ –PdV
It is not possible to calculate work and heat interactions unless the relationships between the thermodynamic properties of the gas are known. Suppose the gas under consideration is an ideal gas (which follows the relation Pv = RT and u = u (T) only) then for an isothermal process,
DU = 0
DQ = PdV = RTdv/v or Q =W = RTln (v2/v1)
Internal energy
Internal energy is the sum of the kinetic energies and the potential energies of the molecules. We denote the internal energy of the system by U. Energy possessed by the atoms or molecules by virtue of their motion is kinetic energy. Since there is a force of attraction between two molecules, they possess some potential energy. The sum of total kinetic and potential energies of atoms or molecules constituting a system is the internal energy of the system. The internal energy of a system depends upon the state of the system. It has a definite value for a definite thermodynamic state. It is not a measurable quantity. If a system starting from one state passes through different states and finally returns to its initial state, then the change in its internal energy will be zero.
Enthalpy
When a process takes place at constant pressure, the heat absorbed or released is equal to the Enthalpy change. Enthalpy is sometimes known as “heat content”, but “enthalpy” is an interesting and unusual word, so most people like to use it. Etymologically, the word “entropy” is derived from the Greek, meaning “turning” and “enthalpy” is derived from the Greek meaning “warming”. As for pronunciation, Entropy is usually stressed on its first syllable, while enthalpy is usually stressed on the second.
Enthalpy (H) is the sum of the internal energy(U) and the product of pressure(P) and volume(V).
Enthalpy H can be written as,
H = U + pV
Where, H = Enthalpy of the system
U = Internal energy of the system
p = Pressure of the system
V = Volume of the system
Enthalpy is not measured directly, however, the change in enthalpy (ΔH) is measured, which is the heat added or lost by the system. It is entirely dependent on the state functions T, p and U.
Enthalpy can also be written as
ΔH=ΔU+ΔPV
At constant temperature, for the process heat flow(q) is equal to the change in enthalpy, this is represented as
ΔH=q
Enthalpy Units
The Enthalpy is expressed as,
H = Energy/Mass
Any physical quantity can be represented by dimensions. The arbitrary magnitudes allocated to the dimensions are called units. There are two types of dimensions namely primary or fundamental and secondary or derived dimensions.
Primary dimensions are: mass, m; length, L; time, t; temperature, T
Secondary dimensions are the ones that can be derived from primary dimensions such as velocity (m/s2), pressure (Pa = kg/m.s2).
There are two unit systems currently available SI (International System) and USCS (United States Customary System) or English system. We, however, will use SI units exclusively in this course. The SI units are based on the decimal relationship between units.