UNIT 4
Electrical Machines
Consider a stator of an electric motor where three-phase winding is physically distributed in the stator core in such a manner that winding of each phase is separated from other by 120o in space.
Although the vector sum of three currents in a balanced three-phase system is zero at any instant, but the resultant of the magnetic fields produced by the currents is not zero rather it will have a constant non-zero value rotating in space in respect to time.
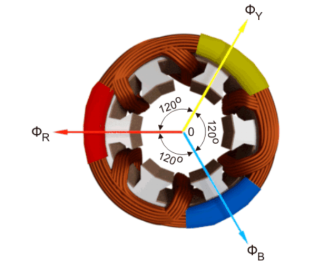
The magnetic flux produced by the current in each phase can be represented by the equations given below. This is a similar representation of current is a three-phase system as the flux is cophasial with the current.
ɸ R = ɸ m sin(wt)
ɸ Y = ɸ m sin(wt -120 0 )
ɸ B = ɸm sin(wt – 240 0 )
Where, φR, φY and φB are the instantaneous flux of corresponding Red, Yellow and Blue phase winding, φm amplitude of the flux wave. The flux wave in the space can be represented as shown below.
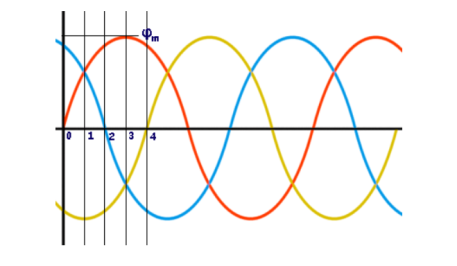
First consider the point 0.
ɸ R = ɸ m sin(0) = 0
The value of
ɸ Y = ɸ m sin(0 – 120 0) = ɸ m sin(-1200) = -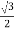 
ɸ m
The value of φB is
ɸ B = ɸm sin(0 – 240 0 )= ɸm sin (-240 0 ) =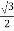 
ɸ m
The resultant of these fluxes at that instant (φr) is 1.5φm which is shown in the figure below.
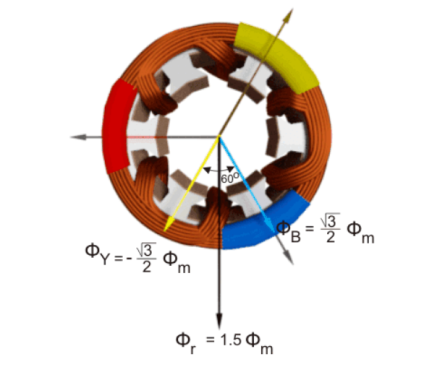
From the graphical representation of flux waves, consider the point 1, where ωt = π / 6 or 30o.
ɸ R = ɸ m sin(30) = ½ ɸ m
The value of
ɸ Y = ɸ m sin(30 – 120 0) = ɸ m sin (-90) = -ɸm.
The value
ɸ B = ɸm sin(30 – 240 0 ) = ɸ m sin (-210) = ½ ɸ m
The resultant of these fluxes at that instant (φr) is 1.5φm which is shown in the figure below. Here it is clear the resultant flux vector is rotated 30o further clockwise without changing its value.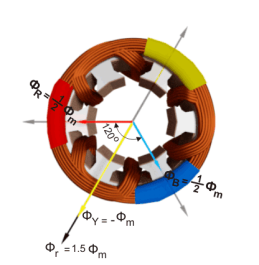
Now, on the graphical representation of flux waves, we will consider the point 2, where ωt = π / 3 or 60o.
ɸ R = ɸ m sin(60) =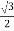 
ɸ m
The value of
ɸ Y = ɸ m sin(60 – 120 0) = ɸ m sin (-60) = -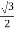 
ɸm.
The value of
ɸ B = ɸ m sin(60 – 240 0) = ɸ m sin (-180) = 0
The resultant of these fluxes at that instant (φr) is 1.5φm which is shown in the figure below. It shows that the resultant flux vector is rotated 30° further clockwise without changing its value.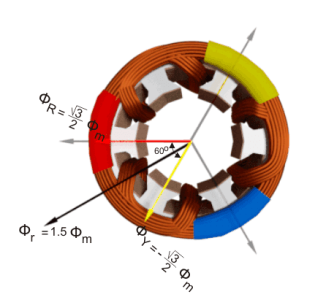
Now, consider the point 3, where ωt = π / 2 or 90o.
ɸ R = ɸ m sin(90) = ɸ m
The value of
ɸ Y = ɸ m sin(90 – 120 0) = ɸ m sin (-30) = -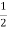 
ɸm.
The value of
ɸ B = ɸ m sin(90 – 240 0) = ɸ m sin (-150) = -1/2 ɸ m.
The resultant of these fluxes at that instant (φr) is 1.5φm which is shown in the figure below. The resultant flux vector is rotated 30o further clockwise without changing its value.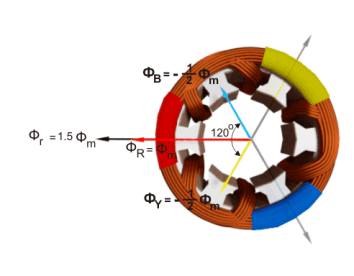
In this way we can prove that the due to balanced supply applied to the three phase stator winding a rotating or revolving magnetic fields is established in the space.
Principle of operation of induction motor:
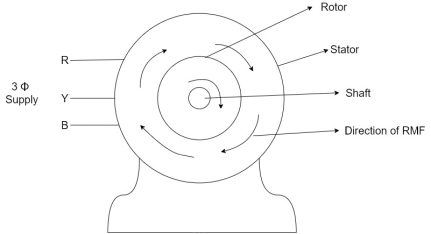
- When the 3Ф A.C supply is connected across the stator of induction motor, the current starts flowing through the stator wdg. i.ethe stator condition.
- Due to this current of flux (Ф) is established in the stator wdg. This flux (Ф) is alternating (changing) in nature. Thus this flux links with the rotor also, and a a Rotating Magnetic Field(RMF) is produced.
- This flux (Ф) induces emf in the rotor also. The RMF is produced in the air gap between stator and rotor.
- The rotor is rotating part which is till stationary, show the rotating magnetic field is cut by stationary rotor and an EMF is induced in the rotor winding. According to faraday's law of EMI the rotor EMF gives the rise to rotor current which opposes the main cause producing it according Lenz's law.
The below curve can be divided into three regions.
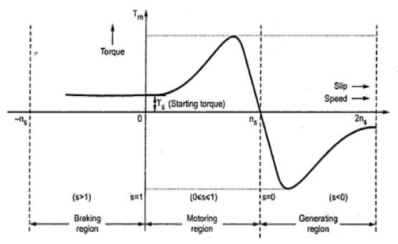
Fig: Torque-Slip Characteristics
i)Motoring Region(0≤s≤1): The induction motor rotates in the same direction as that of the field. Here the speed decreases and torque increases till breakdown torque is reached. In this region air-gap flux is nearly constant. After breakdown torque Tmax , torque decreases and slip increases.
Ii)Generating Region(s<0): In this machine operates as a generator. The rotor rotates at a speed greater than synchronous speed in same direction as that of rotating magnetic field. Due to super synchronous speed the slip becomes negative and creates negative regenerative torque.
Iii)Plugging Region(1≤s≤2): Here slip becomes greater than unity. So, motor rotates in the opposite direction of the rotating magnetic field. Here the stator field is reversed by changing the phase sequence of input supply, due to this the direction of rotating magnetic field also changes. Here torque is positive but speed is negative. So, plugging torque appears as breaking torque. This method of breaking is called plugging.
Que) The stator of a 3-phase induction motor has 5 slots per pole per phase. If supply frequency is 50Hz. Calculate a) number of stator poles produced and total number of slots in stator. b) Speed of rotating stator flux.?
Sol: a) P=2n=2*5=10 poles
Total number of slots= 5 slots/pole/phase * 10 poles * 3 phase=150
a) Ns=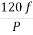
=120x50/10=600rpm
Que) A 3-phase induction motor is wound for 5 poles and is supplied from 50 Hz. Calculate a) synchronous speed b) rotor speed when slip is 4% c) rotor frequency when rotor runs at 500 rpm?
Sol: a) Ns=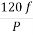
=120x50/5=1200 rpm
b)rotor speed N=Ns(1-s)=1200(1-0.04)=1152 rpm
c)when rotor speed is 500 rpm, slip s=(Ns-N)/Ns=(1200-500)/1200=0.58
Rotor current frequency f’=sf=0.58x50=29.17 Hz
Que) A 3-phase, 50 Hz,3-pole induction motor has a slip of 4%.Calculate a)speed of rotor. B) frequency of rotor emf. If the rotor as a resistance of 2ohm, and standstill reactance of 4ohm,calculate the power factor c)at standstill and d)at a speed of 1200rpm?
Sol: Ns=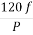
=120x50/3=2000 rpm
a) Speed of rotor N=Ns(1-s)=2000(1-0.04)=1920 rpm
b) Frequency or rotor = f’=sf=0.04x50=2Hz
R2=2ohm, X2=4ohm
Z2=R2+jX2=2+j4=4.47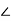
63.43o ohm
c)Power factor cosφ2=0.44(lag)
Slip at speed 1200rpm s=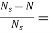
2000-1200/2000=0.4
Rotor impedance at slip s=0.4 is
Z2s=R2+jsX2=2+jx0.4x4=2.56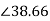
oohm
Power factor at 1200rpm is cos φ2s=cos38.66o=0.78(lag)
Q) A 3-phase induction motor star connected rotor has an induced emf of 70volts between slip rings at standstill on open circuit. The rotor has a resistance and reactance per phase of 1ohm and 5ohm respectively. Calculate current/phase and power factor when slip rings are short circuited?
Sol: Standstill emf/rotor phase=70/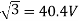
Rotor impedance/phase=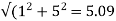
ohm
Rotor current/phase=40.4/5.09=7.92A
Power factor cosφ=0.99
Que) A 3-phase induction motor star connected rotor has an induced emf of 70volts between slip rings at standstill on open circuit. The rotor has a resistance and reactance per phase of 1ohm and 5ohm respectively. Calculate current/phase and power factor when slip rings are connected to star connected rheostat of 2ohm?
Sol: Rotor resistance/phase=2+1=3 ohm
Rotor impedance/phase=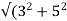
=5.83 ohm
Rotor current/phase= (70/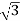
)/5.83=6.93A
Cosφ=3/5.83=0.514
Que) A 6-pole, 3-phase induction motor operates from a supply whose frequency is 50Hz. Calculate i) speed at which the magnetic field of stator is rotating. Ii)speed of rotor when slip is 4%. Iii)frequency of rotor current when slip is 3%?
Sol: i) Stator revolves at synchronous speed. So, Ns=120f/P=120 x 50/6=1000rpm
Ii)rotor speed N=(1-s) Ns= (1-0.04) x 1000=960rpm
Iii)frequency of rotor current f’=sf=0.03 x 50=90rpm
Loss components
In general, we can categorise losses as:
i)Constant losses: They remain constant over the normal working range of induction motor. By no-load test we can find these losses. The losses falling in this category are Iron or core loss, Mechanical Loss and Brush Friction loss.
a)Iron or core loss: The core losses depends on the frequency of supply voltage. As the frequency of rotor is always less than that of stator. Hence, core loss in rotor is less compared to that of stator. The core loss can be further classified as hysteresis and eddy current losses.
b)Mechanical and Brush Friction Loss: These are low at starting and increases with increase in speed. In induction motor speed is usually constant hence these losses also remain constant. Mechanical losses occur in bearings and brush friction losses occur in wound rotor induction motor.
Ii)Variable losses: These losses occur due to current flowing in stator and rotor windings. As the load changes, the current flowing in rotor and stator winding also changes and hence these losses also change. Therefore, these losses are called variable losses. The copper losses are obtained by performing blocked rotor test on three phase induction motor.
Efficiency
Rotor Efficiency=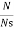
=
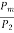
3-phase induction moor efficiency=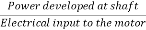
=
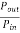
Que) The power input to a rotor of 440V, 50Hz, 6-pole, 3-phase, induction motor is 60kW. The rotor force is observed to make 80 alterations per minute. Calculate i) slip ii) rotor speed iii) rotor cu loss per phase?
Sol: 80 alterations per minute=80/60 cycles per second=1.333Hz=sf
i)slip=1.333/50=0.027 P.u.=2.7%
Ii)Rotor speed N=(1-s) Ns=(1-0.027) x 1000=973.33rpm
Ns=120f/P=120 x 50/6=1000rpm
Iii)rotor cu loss/phase=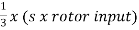
=
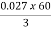=0.54kW
Que) The power input to a 3-phase induction motor is 80kW. The stator loss is total 1kW. Find the mechanical power developed and the rotor cu loss per phase if the slip is 3%?
Sol: P2= stator input – stator losses=80-1=79kW
Pm=(1-s)P2==(1-0.03) x 79=76.63kW
Total rotor cu loss=sP2=0.03 x 79=2.37kW
Rotor cu loss per phase=2.37x1000/3=790W
Que) The power input to a rotor of a 400V, 50hz,6-pole, 3-phaseinduction motor is 15kW. The slip is 4%. Calculate i) frequency of rotor current. i)rotor speed. Iii)rotor cu loss iv) rotor resistance/phase if rotor current is 50A?
Sol: i) frequency of rotor current=sf=0.04 x 50=2Hz
Ii) Rotor speed N=(1-s) Ns=(1-0.04) x 1000=960rpm
Ns=120f/P=120 x 50/6=1000rpm
Iii) rotor cu loss=s x rotor input=0.04 x 15=0.6kW
Iv)rotor cu loss/phase=0.6 x 1000/3=200W
602R2=200
R2=0.055Ω
Starting of induction motor
Direct on-line starter (Full voltage starting method)
In this induction motor is directly connected to the 3-phase supply. The DOL starter applies full line voltage to the motor terminals.
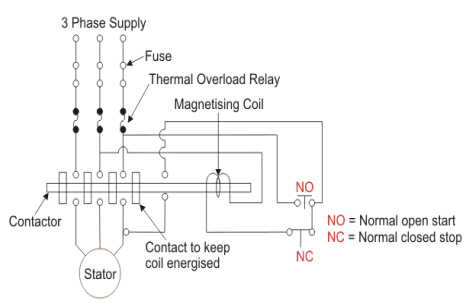
Fig: D.O.L Starter
If the high input current does not cause any excess voltage drop in circuit than only this starter can be used. The value of armature current in motor is given as
Ia=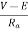
The expression for starting torque is given as
Ts starting torque
Tf Full load torque
If per phase rotor current at full load
Is per phase rotor current at starting
sf full load slip
ss starting slip
R2 rotor resistance
Ws synchronous speed of motor
In induction motor torque is given as
T=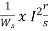
The ratio of starting torque to full load torque is given as
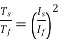x sf
The wiring diagram for a DOL starter is shown above. The working principle of a DOL starter begins with the connection to the 3-phase main with the motor. The control circuit is connected to any two phases and energized from them only. When we press the start button, the current flows through magnetizing coil and control circuit also.
The current energises the contactor coil and leads to close the contacts, and hence 3-phase supply becomes available to the motor. When we stop it, the current discontinues.ss As the supply to motor breaks the machine stops. . The contactor coil (Magnetizing Coil) gets supply even though we release start button because when we release start button, it will get supply from the primary contacts as illustrated in the diagram of the Direct Online Starter.
The advantages of a DOL starter include:
- Simple and most economical starter.
- More comfortable to design, operate and control.
- Provides nearly full starting torque at starting.
- Easy to understand and troubleshoot.
- DOL starter connects the supply to the delta winding of the motor.
The reduced voltage starting methods are:
Star delta starter: The set up for star delta starter is shown below
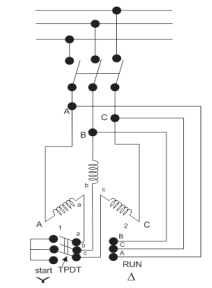
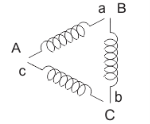
Fig: Star delta starter
The starter phases are connected to star by TPDT (triple pole double throw switch). Initially the TPDT switch is at position 1 and when motor attains steady state switch is thrown to position 2. In position 1 terminals are short circuited and at position 2 a, b and c are connected to B, C and A. The expression for starting torque is given as
Ts starting torque
Tf Full load torque
If per phase rotor current at full load
Is per phase rotor current at starting
sf full load slip
ss starting slip
R2 rotor resistance
Ws synchronous speed of motor
In induction motor torque is given as
T=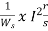
The ratio of starting torque to full load torque is given as
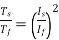x sf
Let V1 line voltage
Iss per phase starting current
Iss=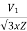
Starting current in stator when connected in delta position
Isd=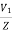
Isd=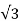
Iss
Then the torque ratio equation will be
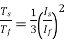x sf
This shows that the reduced voltage method has an advantage of reducing the starting current but the disadvantage is that all these methods of reduced voltage cause the objectionable reduction in the starting torque.
Speed Control: The speed can be controlled by the following methods.
i) Changing stator Pole: This can be done by Multiple stator windings. In stator two windings are provided which are isolated and have different number of poles. By switching we can control the supply to one winding and hence control the speed.
Ii) Supply voltage control: The torque produced is proportional to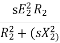 
. The value of 
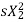is very small and R2 is also constant so T α
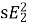. But E2 α V therefore, T α sV2. This equation shows that if supply voltage is decreased the torque also decreases.
Iii) Adding rheostat in the stator: As we already know T α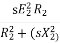 
. The value of 
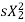is very small and E2 is also constant so T α 
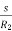. Now if we increase rotor resistance, R2 torque decreases but to supply the same load torque must remain constant. So, we increase slip, which will further result in the decrease in rotor speed. Thus, by adding additional resistance in the rotor circuit, we can decrease the speed of the three-phase induction motor.
Iv) v/f control: There is no direct relation in the speed and torque. At, full load the motor runs at a speed N. When mechanical load increases motor speed decreases till the motor torque again becomes equal to the load torque.
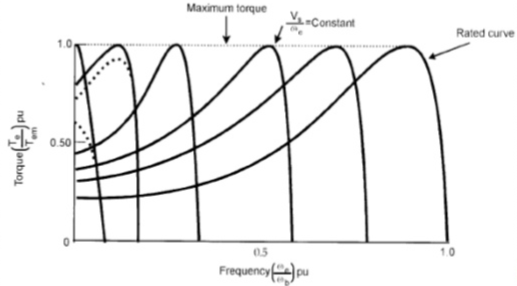
As long as two torques are equal the motor runs at constant speed. When the supply frequency increases the speed increases and reduces the maximum torque of motor. So,
i) F increases, N increases, Tmax decreases.
Ii) V increases, Tmax increases.
A Single-Phase Induction Motor consists of a single phase winding which is mounted on the stator of the motor and a cage winding placed on the rotor. A pulsating magnetic field is produced, when the stator winding of the single-phase induction motor shown below is energized by a single phase supply.
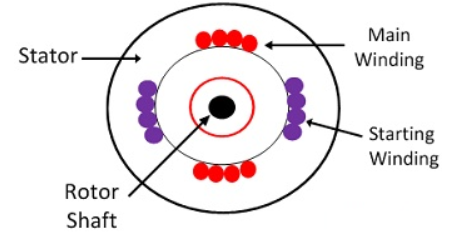
The word Pulsating means that the field builds up in one direction falls to zero and then builds up in the opposite direction. Under these conditions, the rotor of an induction motor does not rotate. Hence, a single-phase induction motor is not self-starting. It requires some special starting means.
If the 1 phase stator winding is excited and the rotor of the motor is rotated by an auxiliary means and the starting device is then removed, the motor continues to rotate in the direction in which it is started.
The performance of the single-phase induction motor is analysed by the two theories. One is known as the Double Revolving Field Theory, and the other is Cross Field Theory. Both the theories are similar and explain the reason to produce torque when the rotor is rotating.
Double Revolving Field Theory of Single- Phase Induction Motor
The double revolving field theory of a single- phase induction motor states that a pulsating magnetic field is resolved into two rotating magnetic fields. They are equal in magnitude but opposite in directions. The induction motor responds to each of the magnetic fields separately. The net torque in the motor is equal to the sum of the torque due to each of the two magnetic fields.
The equation for an alternating magnetic field is given as
b(α) = β max sin w t cos α -----------------------(1)
Where βmax is the maximum value of the sinusoidally distributed air gap flux density produced by a properly distributed stator winding carrying an alternating current of the frequency ω, and α is the space displacement angle measured from the axis of the stator winding.
SinA cosB = ½ sin(A-B) + ½ sin(A+B)
So, the equation (1) becomes
b(α) =1/2 β max sin (w t- α) + ½ β max sin (w t+ α) ------------(2)
The first term of the right-hand side of the equation (2) represents the revolving field moving in the positive α direction. It is known as a Forward Rotating field. Similarly, the second term shows the revolving field moving in the negative α direction and is known as the Backward Rotating field.
The direction in which the single -phase motor is started initially is known as the positive direction. Both the revolving field rotates at the synchronous speed. ωs = 2πf in the opposite direction. Thus, the pulsating magnetic field is resolved into two rotating magnetic fields. Both are equal in magnitude and opposite in direction but at the same frequency.
At the standstill condition, the induced voltages are equal and opposite as a result; the two torques are also equal and opposite. Thus, the net torque is zero and, therefore, a single- phase induction motor has no starting torque.
Separately excited dc motor has field coils similar to that of shunt wound dc motor. The name suggests the construction of this type of motor. Usually, in other DC motors, the field coil and the armature coil both are energized from a single source. The field of them does not need any separate excitation. But, in separately excited DC motor, separate supply Provided for excitation of both field coil and armature coil. Figure below shows the separately excited dc motor.
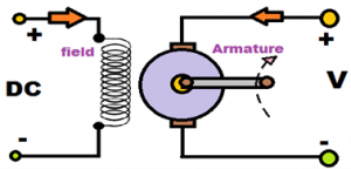
Here, the field coil is energized from a separate DC voltage source and the armature coil is also energized from another source. Armature voltage source may be variable but, independent constant DC voltage is used for energizing the field coil. So, those coils are electrically isolated from each other, and this connection is the specialty of this type of DC motor
In a separately excited motor, armature and field windings are excited form two different dc supply voltages. In this motor,
• Armature current Ia = Line current = IL = I
• Back emf developed , Eb = V – I Ra
where V is the supply voltage and Ra is the armature resistance.
• Power drawn from main supply , P = VI
• Mechanical power developed ,
Pm = Power input to armature – power loss in armature
Operating characteristics of Separately excited dc motor
Both in shunt wound dc motor and separately excited dc motor field is supplied from constant voltage so that the field current is constant. Therefore these two motors have similar speed -armature current and torque – armature current characteristics. In this type of motor flux is assumed to be constant.
• Speed – armature current (N – Ia) characteristics: We know that speed of dc motor is proportional to back emf / flux i.e Eb / φ . When load is increased back emf Eb and φ flux decrease due to armature resistance drop and armature reaction respectively .However back emf decreases more than φ so that the speed of the motor slightly decreases with load.
• Torque – armature current ( τ – Ia) characteristics : Here torque is proportional to the flux and armature current . Neglecting armature reaction, flux φ is constant and torque is proportional to the armature current Ia . τ – Ia characteristics is a straight lien passing through the origin. From the curve we can see that huge current is needed to start heavy loads. So this type of motor do not starts on heavy loads.
Speed control of separately excited DC motor
Speed of this type of dc shunt motor is controlled by the following methods:
I. Field control methods: Weakening of field causes increase in speed of the motor while strengthening the field causes decreases the speed. Speed adjustment of this type of motor is achieved from the following methods:
II. Field rheostat control: – Here a variable resistance is connected in series with the field coil. Thus the speed is controlled by means of flux variation.
Reluctance control involving variation of reluctance of magnetic circuit of motor.
Field voltage control by varying the voltage at field circuit while keeping armature terminal voltage constant.
III. Armature control methods: Speed adjustment of separately excited DC motor by armature control may be obtained by any one of the following methods :
i. Armature resistance control: – Here, the speed is controlled by varying the source voltage to armature. Generally, a variable resistance is provided with the armature to vary the armature resistance.
ii. Armature terminal voltage control involving variation of variation of voltage in armature circuit.
Applications OF DC Motors
Separately excited dc motors have industrial applications. They are often used as actuators. This type of motors is used in trains and for automatic traction purposes.
The synchronous generator or alternator is an electrical machine that converts the mechanical power from a prime mover into an AC electrical power at a particular voltage and frequency.
The synchronous motor always runs at a constant speed called synchronous speed.
It works on the principle of Faraday laws of electromagnetic induction. The electromagnetic induction states that electromotive force induced in the armature coil if it is rotating in the uniform magnetic field.
The EMF will also be generated if the field rotates and the conductor becomes stationary. Thus, the relative motion between the conductor and the field induces the EMF in the conductor. The wave shape of the induces voltage always a sinusoidal curve.
Construction of Synchronous Generator
The rotor and stator are the rotating and the stationary part of the synchronous generator. They are the power generating components of the synchronous generator.
The rotor has the field pole, and the stator consists the armature conductor. The relative motion between the rotor and the stator induces the voltage between the conductor.
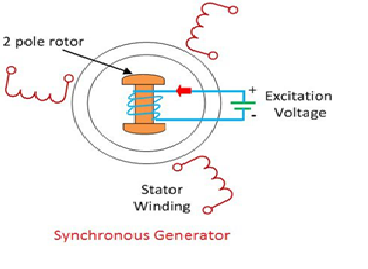
Applications of Synchronous Generator
- The three-phase synchronous generators have many advantages in generation, transmission and distribution.
- The large synchronous generators use in the nuclear, thermal and hydropower system for generating the voltages.
- The synchronous generator with 100MVA power rating uses in the generating station. The 500MVA power rating transformer use in the super thermal power stations.
- The synchronous generators are the primary source of the electrical power. For the heavy power generation, the stator of the synchronous generator design for voltage ratings between 6.6 kV to 33 kV.
Text-Books/Reference-Books:
- Basic Electrical Engineering - D.P. Kothari and I.J. Nagrath, 3rd edition 2010, Tata McGraw Hill.
- D.C. Kulshreshtha, “Basic Electrical Engineering”, McGraw Hill, 2009.
- L.S. Bobrow, Fundamentals of Electrical Engineering”, Oxford University Press, 2011
- Electrical and Electronics Technology, E. Hughes, 10th Edition, Pearson, 2010
- Electrical Engineering Fundamentals, Vincent Deltoro, Second Edition, Prentice Hall India, 1989.
