UNIT 4
Development of Surfaces
Imagine that a solid is enclosed in a wrapper of thin material, such as paper. If this covering is opened out and laid on a flat plane, the flattened-out paper is thedevelopment of the solid. Thus, when surfaces of a solid are laid out on a plane,the figure obtained is called itsdevelopment.
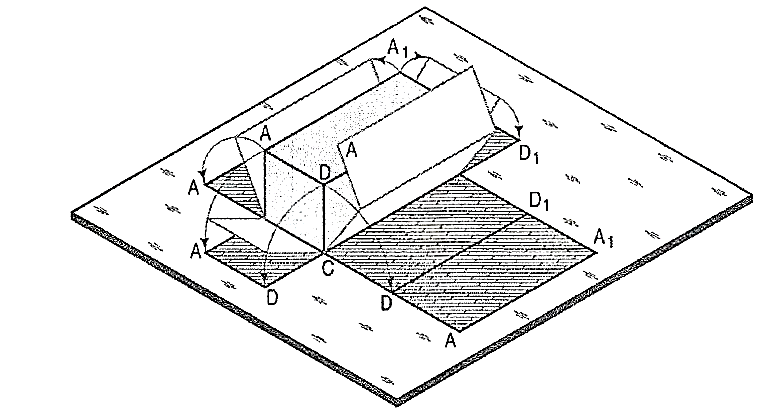
Figure 1
Fig. 1 shows a square prism covered with paper in process of being opened out. Its development (fig. 2) consists of four equal rectangles for the faces and two similar squares for its ends. Each figure shows the true size and shape of the corresponding surface of the prism. The development of a solid, thus represents the actual shape of all its surfaces which, when bent or folded at the edges, would form the solid.
Hence, it is very important to note that every line on the development must be the true length of the corresponding edge on the surface.
The knowledge of development of surfaces is essential in many industries such as automobile, aircraft, ship building, packaging and sheet-metal work. In construction of boilers, bins, process-vessels, hoppers, funnels, chimneys etc., the plates are marked and cut according to the developments which, when folded, form the desired objects. The form of the sheet obtained by laying all the outer surfaces of the solid with suitable allowances for the joints is known as pattern.
Only the surfaces of polyhedral (such as prisms and pyramids) and single curved surfaces (as of cones and cylinders) can be accurately developed. Warped and double-curved surfaces are undevelopable. These can however be approximately developed by dividing them up into many parts.
This chapter deals with the following topics:
1. Methods of development.
2. Developments of lateral surfaces of right solids.
3. Development of transition pieces.
4. Spheres (approximate method).
The following are the principal methods of development:
1. Parallel-line development:
It is employed in case of prisms and cylinders in which stretch-out-line principle is used. Lines A-A and A1-A1in fig.2 are called the stretch-out Ines.
2. Radial-line development:
Itis used for pyramids and cones in which the true length of the slant edge or the generator is used as radius.
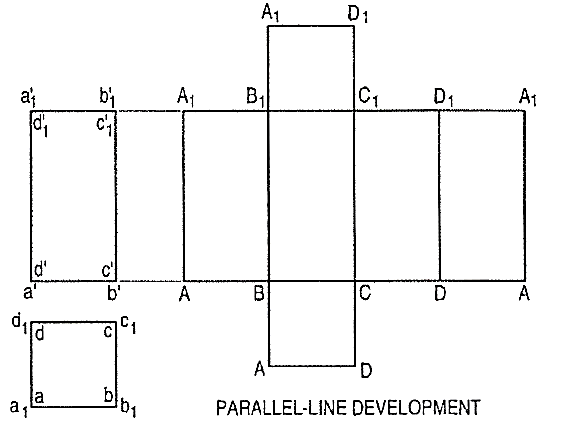
Figure 2
3. Triangulation development:
This is used to develop transition pieces. This is simply a method of dividing a surface into many triangles and transferring them into the development.
4. Approximate method:
It is used to develop objects of double curved orwarped surfaces as sphere, paraboloid, ellipsoid, hyperboloid and helicoid.
Developments of lateral surfaces of right solids:
The methods of drawing developments of surfaces of various solids are explainedby means of the following typical problems. Only the lateral surfaces of the solids (except the cube) have been developed. The ends or bases have been omitted. Theycan be easily incorporated if required.
Cube
The development of the surface of a cube consists of six equal squares, the lengthof the side of the squares being equal to the length of the edge of the cube.
Problem:
1. Draw the development of the surface of the part P of the cube,the front view of which is shown in fig. 3(i)Name all the corners of the cube and the points at which the edges are cut.
(i) Draw the stretch-out lines A-A and E-E directly in line with the front view, andassuming the cube to be whole, draw four squares for the vertical faces, onesquare for the top and another for the bottom as shown in fig. 3(ii).
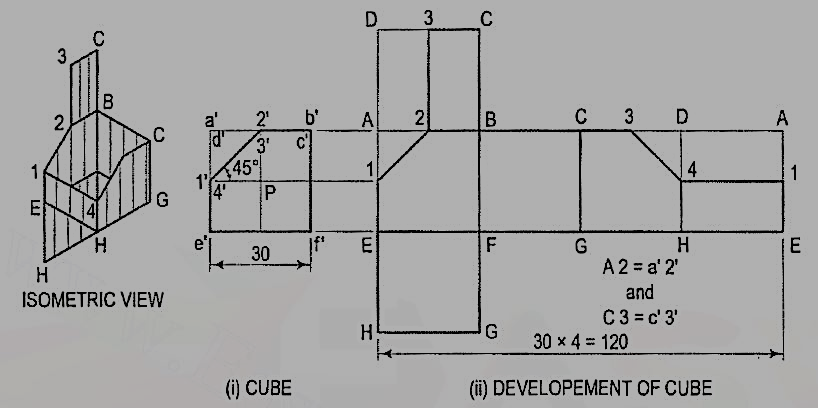
Figure 3
(ii) Name all the corners. Draw a horizontal line through 1' to cut AE at 1 andDH at 4. a' b' is the true length of the edge. Hence, mark a point 2 onAB and 3 on CD such that A 2 = a' 2' and C 3 = c' 3'. Mark the point3 on CD in the top square also.
(iii) Draw lines 1-2, 2-3, 3-4 and 4-1, and complete the development as shown.Keep lines for the removed portion, viz. A1, A2, 3D, D4 and DA thin and fainter.
2. Draw the development of the surface of the part P of the cubeshown in two views in fig. 4(i).
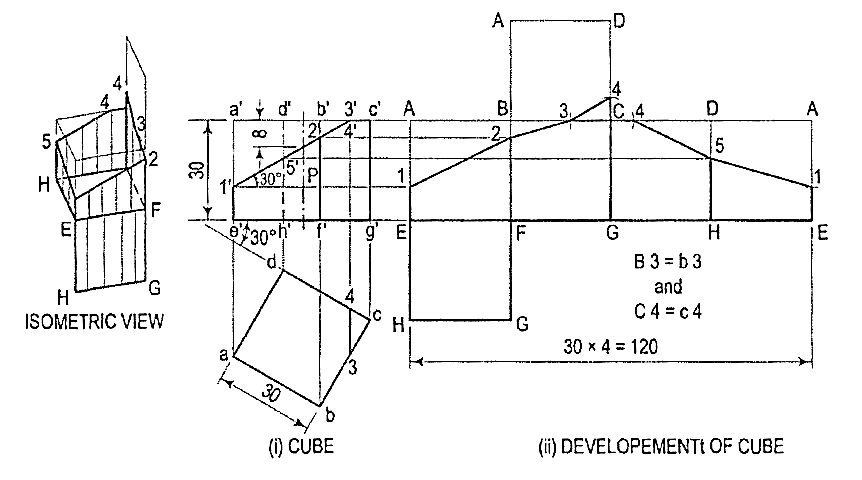
Figure 4
(i) Draw horizontal lines through points 1 ', 2' and 5' to cut AE in 1, BF in 2and DH in 5 respectively. Lines b'c' and c'd' do not show the true lengthsof the edges. The sides of the square in the top view show the true length.Therefore, mark points 3 in BC and 4 in CD such that 83 = b3 and C4 = c4.
(ii) Draw lines joining 1, 2, 3 etc. in correct sequence and complete the requireddevelopment. Keep the lines for the removed part fainter.
Prisms:
Development of the lateral surface of a prism consists of the same number ofrectangles in contact as the number of the sides of the base of the prism. Oneside of the rectangle is equal to the length of the axis and the other side equalto the length of the side of the base.
Problem:
3. Draw the development of the lateral surface of the part P of thepentagonal prism shown in fig. 3 (i).
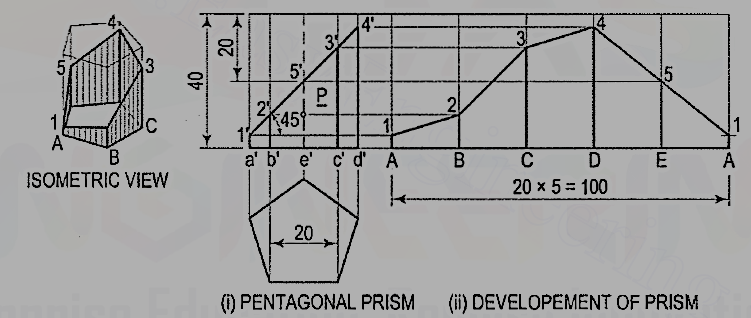
Figure 5
Name the corners of the prism and the points at which the edges are cut.
(i) Draw the development assuming the prism to be whole [fig. 5(ii)]. It is made up of five equal rectangles.
(ii) Draw horizontal lines through points 1’, 2’ etc. to cut the lines for the corresponding edges in the development at points 1, 2 etc.
(iii)Draw lines joining these points and complete the development as shown.
4. Draw the development of the lateral surface of the part P of thehexagonal prism shown in fig. 6 (i).
Name the points at which the edges are cut and draw the developmentassuming the prism to be whole [fig. 6(ii)].
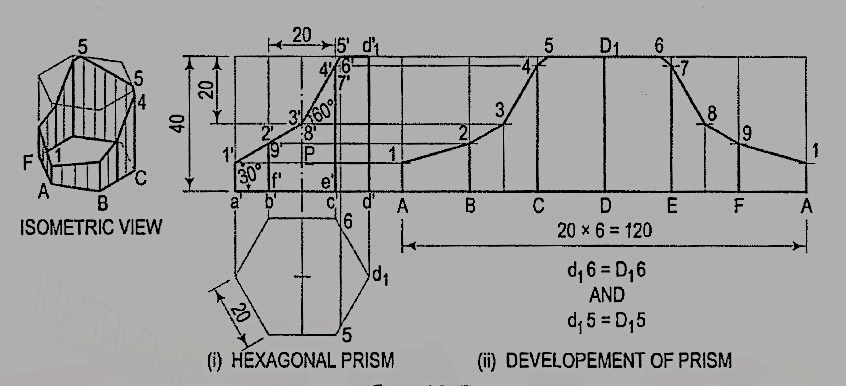
Figure 6
(i) Obtain all the points except 5 and 6 by drawing horizontal lines. Note thatpoints 3 and 8 lie on vertical lines drawn through the mid-points of BC and EF.
(ii) Mark points 5 and 6 such that SD1 = 5d1 and D16 = d16.
(iii) Draw lines joining points 1, 2, 3 etc. in correct sequence and complete therequired development as shown.
Cylinders
The development of the lateral surface of a cylinder is a rectangle having one sideequal to the circumference of its base-circle and the other equal to its length.
Problem
1. Develop the lateral surface of the truncated cylinder shown infig. 7(i).
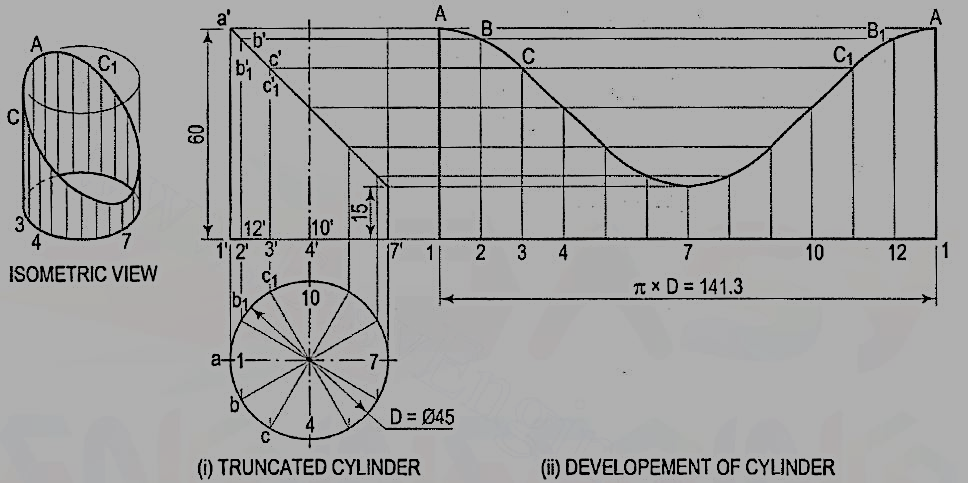
Figure 7
(i) Divide the circle in the top view into twelve equal parts. Project the divisionpoints to the front view and draw the generators. Mark points a', b' andb'1, c' and c'1 etc. in which the generators are cut.
(ii) Draw the development of the lateral surface of the whole cylinder alongwith the generators [fig. 7(ii)]. The length of the line 1-1 is equalto π x D (circumference of the circle). This length can also be markedapproximately by stepping off with a bow divider, twelve divisions, eachequal to the chord-length ab. (The length thus obtained is about 1 %shorter than the exact length; but this is permitted in drawing work.)
(iii) Draw horizontal lines through points a', b' and b'1 etc. to cut the correspondinggenerators in points A, B and B1 etc. Draw a smooth curve through thepoints thus obtained. The figure 1-A-A-1 is the required development.
Pyramids
The development of the lateral surface of a pyramid consists of many equalisosceles triangles in contact. The base and the sides of each triangle are respectivelyequal to the edge of the base and the slant edge of the pyramid.
Method of drawing the development of the lateral surface of a pyramid:
(i) With any point O as centre and radius equal to the true length of the slantedge of the pyramid, draw an arc of the circle. With radius equal to the truelength of the side of the base, step-off (on this arc) the same number ofdivisions as the number of sides of the base.
(ii) Draw lines joining the division-points with each other in correct sequenceand with the centre for the arc. The figure thus formed (excluding thearc) is the development of the lateral surface of the pyramid.
Problem:
1. Draw the development of the lateral surface of the part P ofthe triangular pyramid shown in fig. 8 (i). The line o'1' in the front view is thetrue length of the slant edge because it is parallel to xy in the lop view. The truelength of the side of the base is seen in the top view.
(i) Draw the development of the lateral surface of the whole pyramid [fig. 8(ii)]as explained above. On 01 mark a point A such that OA = o'a'. o'2' (withwhich o'3' coincides) is not the true length of the slant edge.
(ii) Hence, through b', draw a line parallel to the base and cutting o' a' at b".o'b" is the true length of o'b' as well as o'c'. Mark a point B in 02 andC in 03 such that OB = OC = o'b".
(iii) Draw lines AB, BC and CA and complete the required development as shown.Keep the arc and the lines for the removed part fainter.
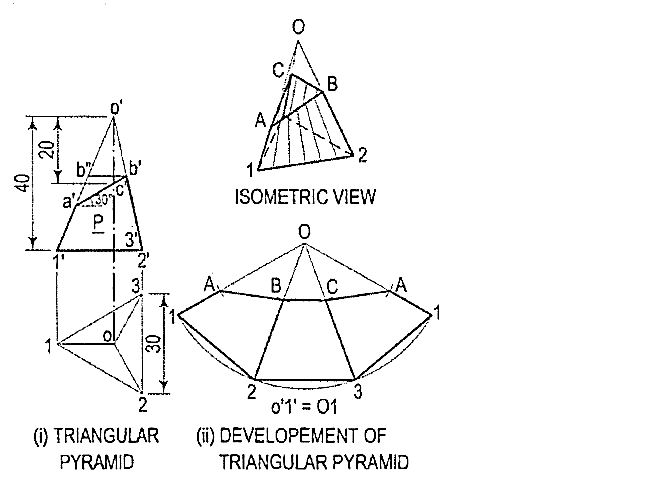
Figure 8
2. Draw the development of the lateral surface of the frustum ofthe square pyramid shown in fig. 9 (i).
(i) Determine the position of the apex. None of the lines in the front viewshows the true length of the slant edge. Therefore, draw the top view andmake any one line (for the slant edge) horizontal, i.e. parallel to xy and determine the true length o'1 '1. Through a', draw a line parallel to the baseand obtain the true length o'a".
(ii) With O as centre and radius o'1 '1, draw an arc and obtain the developmentof the lateral surface of the whole pyramid [fig. 9(ii)].
(iii) With centre O and radius o' a", draw an arc cutting O1, O2 etc. at pointsA, B etc. respectively.
(iv) Draw lines AB, BC, CD and DA and complete the required development.Note that these lines are respectively parallel to lines 1-2, 2-3 etc.
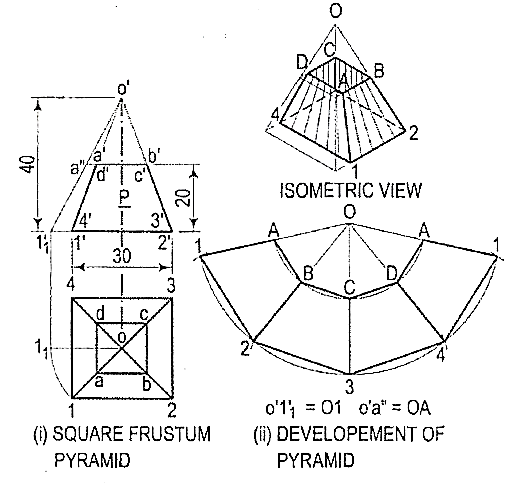
Figure 9
3.A frustum of a square pyramid has its base 50 mm side; top 25 mm side and height 75 mm. Draw the development of its lateral surface.
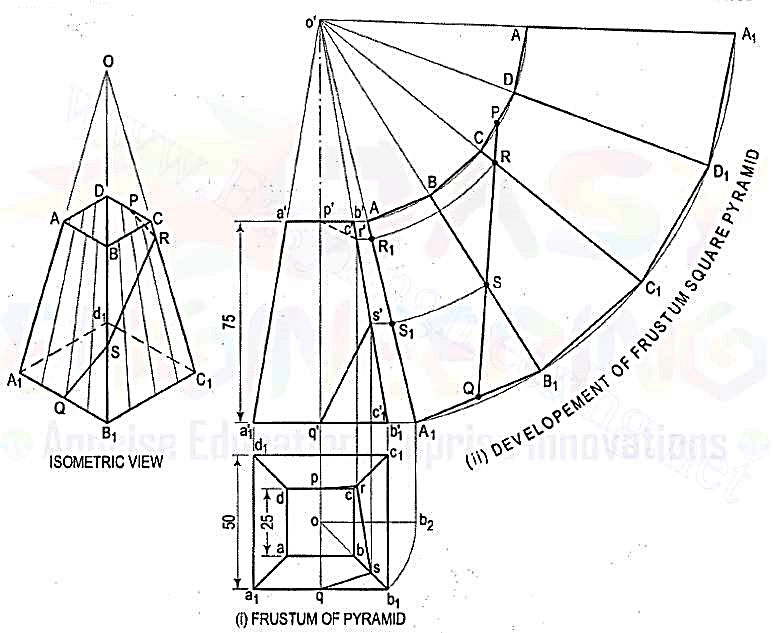
Figure 10
(i) Mark the mid-point P of CD and Q of A1B1. Draw a line joining P and Q andcutting CC1 at R and BB1 at S. Transfer these points to the front view and thetop view. For example, with o' as centre and radius o'R, draw an arc cuttingo' A1 at R1. Through R1, draw a line parallel to the base and cutting c'c'1 at r'.Project r' to r on cc1 in the top view. r' and r are the projections of R.
(ii) Similarly, obtain s' and s on b'b'1 and bb1 respectively. Draw lines pr, rs and sq which will show the top view of the line PQ. p'r's'q' will be the path of the line PQ in the front view.
Cone
The development of the curved surface of a cone is a sector of a circle, the radiusand the length of the arc of which are respectively equal to the slant height andthe circumference of the base-circle of the cone.
Problem:
1. Draw the development of the lateral surface of the truncatedcone shown in fig. 11 (i).
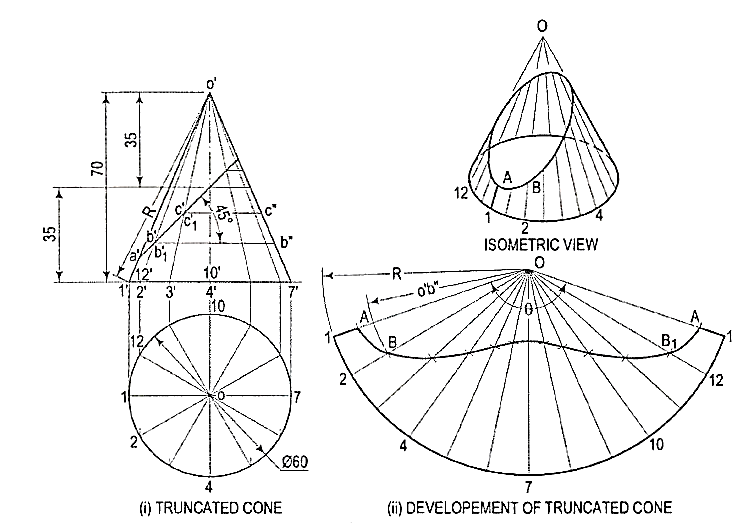
Figure 11
Assuming the cone to be whole, let us draw its development.
(i) Draw the base-circle in the top view and divide it into twelve equal parts.
(ii) With any point O as centre and radius equal to o'1' or o'7', draw an arcof the circle [fig. 15-24(ii)]. The length of this arc should be equal to thecircumference of the base circle. This can be determined in two ways.
(iii) Calculate the subtended angle θ by the formula,
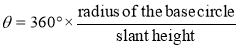
Cut-off the arc so that it subtends the angle θ at the center and divide it into twelve equal parts.
(iv) Step-off with a bow-divider, twelve equal divisions on the arc, each equalto one of the divisions of the base-circle.
(This will give an approximate length of the circumference. Note thatthe base-circle should not be divided into less than twelve equal parts.)
(v) Join the division-points with 0, thus completing the development of thewhole cone with twelve generators shown in it [fig. ,11(ii)].
(vi) The truncated portion of the cone may be deducted from this development bymarking the positions of points at which generators are cut and then drawinga curve through them. For example, generators o'2' and o'12' in the front vieware cut at points b' and b'1 which coincide with each other. The true length ofo' b' may be obtained by drawing a line through b', parallel to the base andcutting o'7' at b". Then o'b" is the true length of o'b'.
(vii) Mark points B and 81 on generators 02 and 0-12 respectively, such thatOB = 0B1 = o' b". Locate all points in the same way and draw a smoothcurve through them. The figure enclosed this curve and the arc is thedevelopment of the truncated cone.
2. Draw the development of the lateral surface of the part P ofthe cone shown in fig. 12
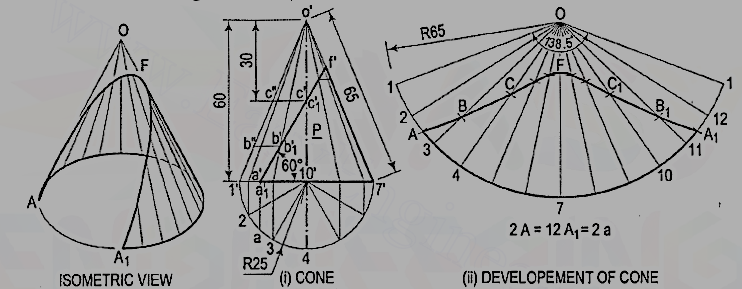
Figure 12
Draw the development as explained in problem [fig. 12 (ii)]. For thepoints at which the base of the cone is cut, mark points A and A1 on the arcs2-3 and 11-12 respectively, such that A2 = A1 12 = a2. Draw the curve passingthrough the points A, B, C etc. The figure enclosed between this curve and the arcA-A1 is the required development.
3. Draw the projections of a cone resting on the ground on itsbase and show on them, the shortest path by which a point P, starting from a pointon the circumference of the base and moving around the cone will return to thesame point. Base of cone 61 mm diameter; axis 75 mm long.
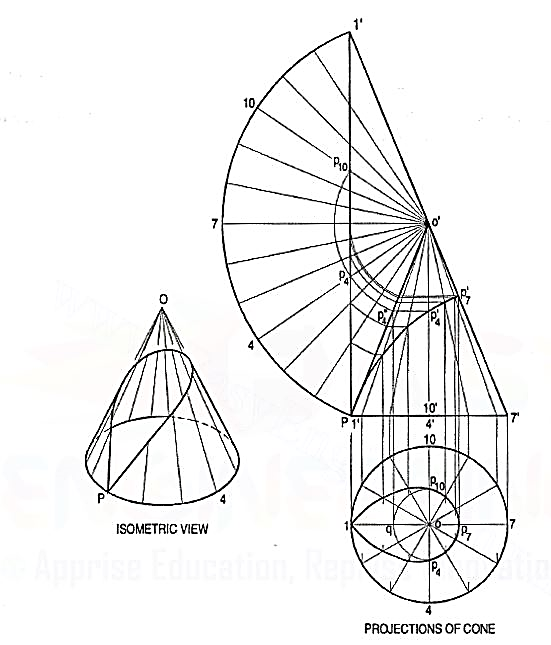
Figure 13
(i) Draw the projections and the development of the surface of the coneshowing all twelve generators (fig. 13). The development may be drawnattached to o'1 '.
(ii) Assume that P starts from the point 1 (i.e. point 1' in the front view).Draw a straight line 1 '1' on the development. This line shows the requiredshortest path.Let us take a point P4 at which the path cuts the generator o’4. Mark a point P"4 on o'1' such that o'P"4 = o'P4. This can be doneby drawing an arc with o' as centre and radius equal to o'P 4 cutting o11'at P"4. Through P"4, draw a line parallel to the base cutting o'4' at P'4.Then p'4 is the position of the point p4 in the front view.Similarly, transfer all the points to the front view and draw therequiredcurve through them. The curve at the back will coincide with the frontcurve.
(iii) Project these points to the top view on the respective generators. p'4 andp'10 cannot be projected directly. Hence, project p"4 to a point q on o1.With o as centre and radius equal to oq, draw an arc cutting o4 at p4 ando-10 at p10. Thus op4 = op10 = oq. A curve drawn through the pointsthus obtained will show the path in the top view.
Development of transition pieces:
Pipes are used in many industries to convey hot or cold fluids. When two differentsizes and shapes of pipes are joined using special pipe joint which is known astransition piece. In most cases, transition pieces are composed of plane surfacesand conical surfaces, the latter being developed by triangulation.
Problem:
1. In air-conditioning system a rectangular duct of 100 mm x 50 mmconnects another rectangular duct of 50 mm x 25 mm through the transition pieceas shown in fig. 14(i). Neglecting thickness of a metal sheet, develop the lateralsurface of the transition piece as shown in fig. 14(ii).
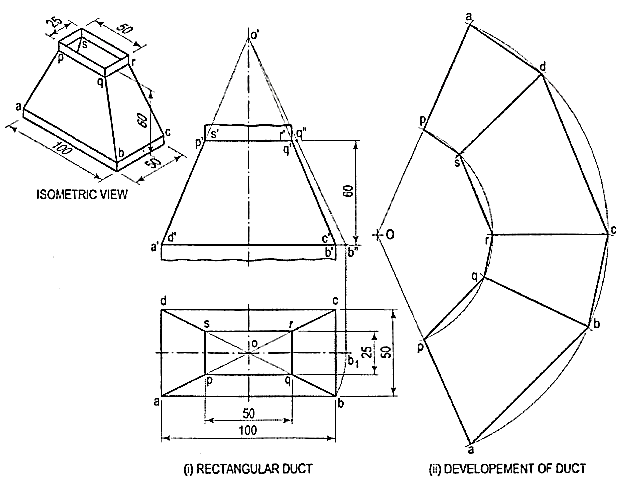
Figure 14
The transition piece is a frustum of a rectangular pyramid.
(i) Determine the position of the apex of the pyramid by extending a'p' and b'q' as shown. None of the lines in the front view shows the true length of theslant edge. Therefore, draw the top view and make any slant line parallel to xy and determine its true length o'b".
(ii) With O as centre and radius o'b", draw an arc and obtain the development ofa whole pyramid as shown.
(iii) With O as centre and radius o'q", draw an arc cutting oa, ob, oc at points p, q, etc.respectively. Join them in sequence and complete the development as shown.
2. An air-conditioning duct of a square cross-section70 mm x 70 mm connects a circular pipe of 40 mm diameter through the transitionpiece. Draw the projections and develop the lateral surface of the transition piece.
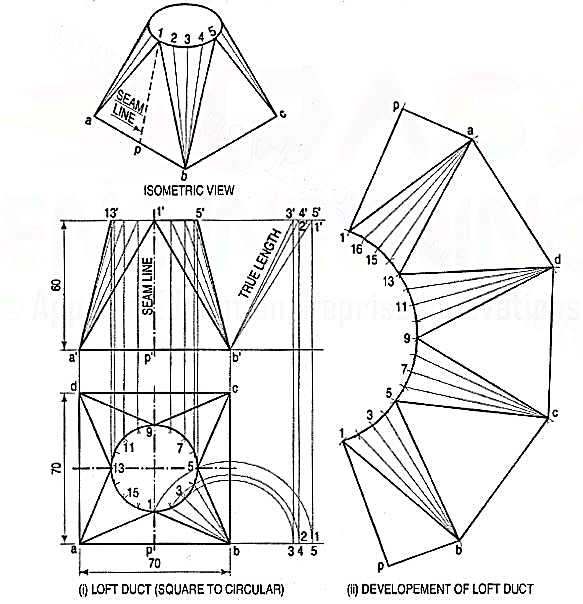
Figure 15
(i) Draw the front view and the top view as shown in fig. 15 (i).
(ii) Divide the top view of circle into some convenient divisions, say 16 parts as shown.
(iii) Note that the transition piece is composed of four isosceles triangles andfour conical surfaces. The seam is a long line 1-P.
(iv) Begin the development from the seam line 1-P (1 '-P'). As shown in fig. 15(ii)draw the right-angle triangle 1-P-b, whose base pb is equal to half the sideab and whose hypotenuse 1-b is equal to the true length 1 '-b' of side 1-b.
(v) The conical surfaces are developed by the triangulation method as follows.(vi) In the top view, join division of the circle 1, 2, 3 etc. with the corner a,b, c and d. Project them in the front view as shown. Obtain the truelength of sides of each triangle as shown.
(vii) With b as centre and 2'b' (true length) radius draw an arc, cutting thearc drawn with 1' as centre and 1 '2' as radius. Similarly, obtain thepoints 3', 4', 5' etc. Join them in the proper order as shown.
Introduction
The intersecting surfaces may be two plane surfaces or two curved surfaces of solids. The lateral surface of every solid taken as a whole is a curved surface. This surface may be made of only curved surface as in case of cylinders, cones etc. or of plane surfaces as in case of prisms, pyramids etc. In the former case, the problem is said to be on the intersection of surfaces and in the latter case, it is commonly known as the problem on interpenetration of solids. It may, however, be noted that when two solids meet or join or interpenetrate, it is the curved surfaces of the two that intersect each other.
In this chapter, we will learn,
1. Line of intersection
2. Methods of determining the line of intersection between surfaces of two interpenetrating solids.
3. Intersection of two prisms
4. Intersection of cylinder and cylinder
5. Intersection of cylinder and prism
6. Intersection of cone and cylinder
7. Intersection of cone and prism
8. Intersection of cone and cone
9. Intersection of sphere and cylinder or prism.
Line of Intersection
In engineering practice, objects constructed may have constituent parts, the surfaces of which intersect one another in lines which are called lines of intersection. A dome fitted on a boiler is one such example. The surface of the dome extends up to the line of intersection only. For accurate development of the surface of the dome, this line of intersection must be accurately located and shown in two orthographic views. The shape of the hole to be cut in the boiler-shell is also determined from the shape of the same line of intersection.
Thus, the line of intersection of the two surfaces is a line common to both. It is composed of points at which the lines of one surface intersect those on the other surface. The line of intersection may be straight or curved, depending upon the nature of intersecting surfaces.
Two plane surfaces (e.g. Faces of prisms and pyramids) intersect in a straight-line. The line of intersection between two curved surfaces (e.g. Of cylinders and cones) or between a plane surface and a curved surface is a curve.
When a solid completely penetrates another solid, there will be two lines of intersection. These lines are, sometimes, called the lines or curves of interpenetration. The portion of the penetrating solid which lies hidden within the other solid is shown by dotted lines.
Methods of determining the line of intersection between surfaces of two interpenetrating solids
(1) line method: A number of lines are drawn on the lateral surface of one of the solids and in the region of the line of intersection. Points of intersection of these lines with the surface of the other solid are then located. These points will obviously lie on the required line of intersection. They are more easily located from the view in which the lateral surface of the second solid appears edgewise (i.e. as a line). The curve drawn through these points will be the line of intersection.
(2) Cutting-plane method: The two solids are assumed to be cut by a series of cutting planes. The cutting planes may be vertical (i.e. perpendicular to the H.P.), edgewise (i.e. perpendicular to the V.P.) or oblique. The cutting planes are so selected as to cut the surface of one of the solids in straight lines and that of the other in straight lines or circles.
Intersection of two prisms:
Prisms have plane surfaces as their faces. The line of intersection between two plane surfaces is obtained by locating the positions of points at which the edges of one surface intersect the other surface and then joining the points by a straight-line. These points are called vertices (plural of vertex). The line of intersection between two prisms is therefore a closed figure composed of many such lines meeting at the vertices.
It is determined by locating the points at which edges of one prism intersect edges or faces of the other prism and then joining them in correct sequence.
Problem:
1. (fig. 1) A vertical square prism, base 50 mm side, is completely penetrated by a horizontal square prism, base 35 mm side, so that their axes intersect. The axis of the horizontal prism is parallel to the V.P., while the faces of the two prisms are equally inclined to the V.P. Draw the projections of the solids, showing lines of intersection. (Assume suitable lengths for the prisms.)
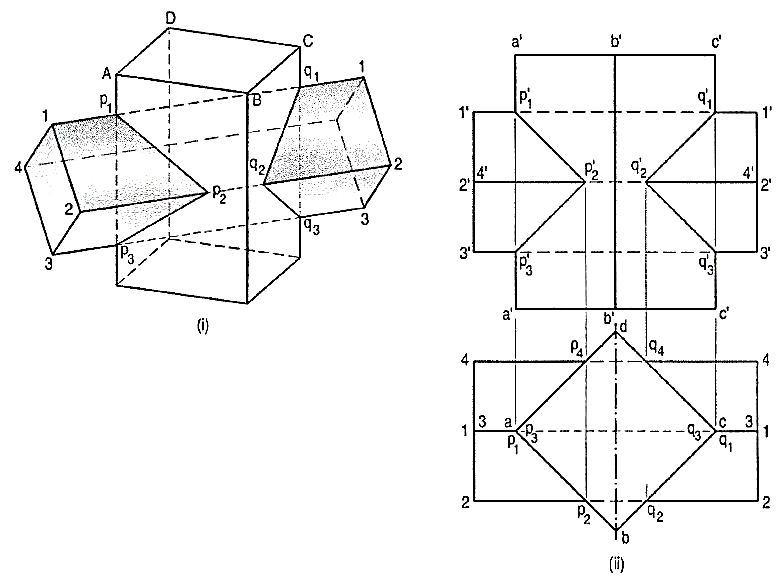
Figure 1
(i) Draw the projections of the prisms in the required position. The faces of the vertical prism are seen as lines in the top view. Hence, let us first locate the points of intersection in that view.
(ii) Lines 1-1 and 3-3 intersect the edge of the vertical prism in points p1 and p3(coinciding with a). Lines 2-2 and 4-4 intersect the faces at p2 and p4 respectively. The exact positions of these points along the length of the prism may now be determined by projecting them on corresponding lines in the front view. For example, p2 is projected to p'2 on the line 2'2'. Note that p'4 coincides with p'2.
(iii) Draw lines p'1 p'2 and p'2 p'3• Lines p'1 p’4and p' 3 p'4 coincide with the front lines. These lines show the line of intersection. Lines q'1q'2 and q'2q'3 on the other side are obtained in the same manner. Note that the lines for the hidden portion of the edges are shown as dashed lines. The portions p'1 p'3 and q'1q'3 of vertical edges a'a' and c'c' do not exist and hence, must be removed or kept fainter.
Problem 2:
A vertical square prism, base 50 mm side is completely penetrated by a horizontal square prism, base 35 mm side so that their axes are6 mm apart. The axis of the horizontal prism is parallel to the V.P., while the faces of both prisms are equally inclined to the V.P. Draw the projections of the prisms showing lines of intersection. (fig. 2)
Points p'1 ... p'4 at which edges of the horizontal prism intersect faces of the vertical prism may be located from the top view. In addition to these points, it will be necessary to find points at which edges of the vertical prism are cut. They will be the points at which these edges intersect the faces of the horizontal prism.
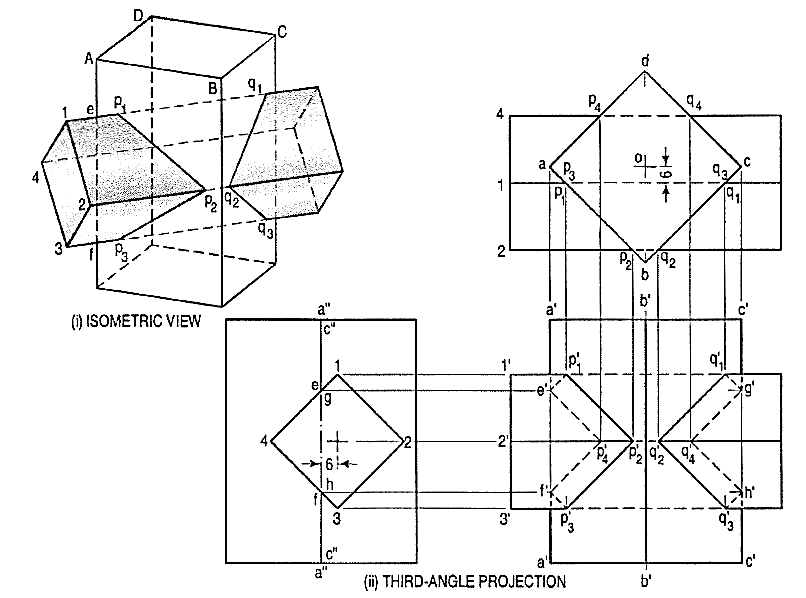
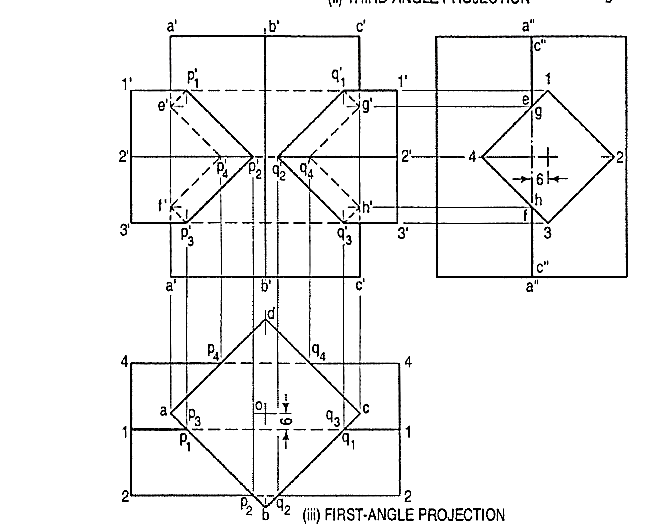
Figure 2
(i) For this purpose, draw the side view. In this view, all faces of the horizontal prism are lines. Mark points e and f at which the line a"a" intersects the faces. Project these two points to e' and f' on the line a'a' in the front view. Join all the points of intersection in correct sequence. Care must be taken to determine visible and hidden lines. Only two lines viz. p'1 p'2 and p'2 p'3 are visible.
(ii) Locate points (on the other side) at which the edges come out and the two points g' and h' at which the edge c'c' is cut.
(iii) Draw lines joining these points. They will be exactly like lines p'1 p'2 etc. on the left-hand side.
Intersection of Cylinder and Cylinder:
As cylinders have their lateral surfaces curved, the line of intersection between them will also be curved. Points on this line may be located by any one of the two methods. For plotting an accurate curve, certain critical or key points, at which the curve changes direction, must also be located. These are the points at which; outermost or extreme lines of each cylinder pierce the surface of the other cylinder.
In prisms, vertices are the key points.
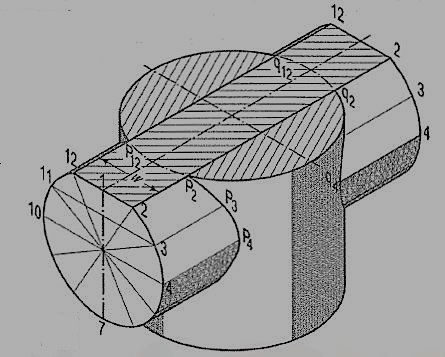
Figure 3
Problem:
1. A vertical cylinder of 80 mm diameter is completely penetrated by another cylinder of 60 mm diameter their axes bisecting each other at right angles. Draw their projections showing curves of penetration, assuming the axis of the penetrating cylinder to be parallel to the V.P.
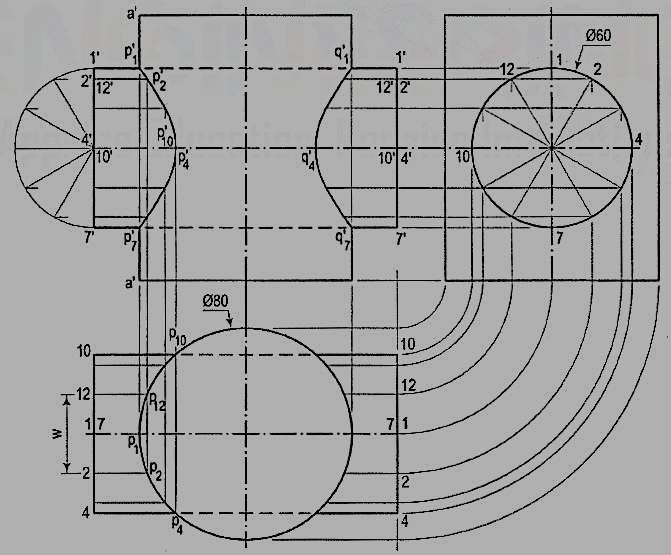
Figure 4
Draw the front view and the top view and show lines for twelve generators in the horizontal cylinder in both views.
(a) Line method:
(i) Mark points p1, p2 etc. at which lines 1-1, 2-2 etc. intersect the circle (showing the surface of the vertical cylinder) in the top view and project them to p'1, p'2 etc. on corresponding lines 1 '1 ', 2'2' etc. in the front view.
(ii) Draw the required curves on both sides of the axis through points thus located. Hidden portions of the curves coincide with the visible portions. Points p'1, p'4 , p'7 and p'10 are the key points where the curve changes direction.
(b) Cutting-plane method: It will be seen that in this problem, there is practically no difference between the line method and the cutting-plane method. But the latter method proves more useful in solving problems in which none of the projections shows a line-view of the surface of a solid. Assume a series of horizontal cutting planes passing through the lines on the horizontal cylinder and cutting both cylinders. Sections of the horizontal cylinder will be rectangles, while those of the vertical cylinder will always be circles of the same diameter as its own. Points at which sides of the rectangles intersect the circle will lie on the curve of intersection. For example, let a horizontal section plane through points 2 and 12 [fig. 3)].
In the front view, it will be a line coinciding with the line 2' 2'. The section of the horizontal cylinder will be a rectangle of width w (i.e. the line 2-12). The section of the vertical cylinder will be a circle. Points p2 and p12 at which the sides (2-2 and 12-12) of the rectangle cut the circle, lie on the curve. These points are first marked in the top view [fig. 4] and then projected to points p'2 and p'12 on lines 2' 2' and 12'-12' in the front view. Points on the other side of the vertical axis are in the same manner.
2. (fig 5) A vertical cylinder of 75 mm diameter is penetrated by another cylinder of the same size. The axis of the penetrating cylinder is parallel to both the H.P. And the V.P. And is 9 mm away from the axis of the vertical cylinder. Draw the projections showing curves of intersection.
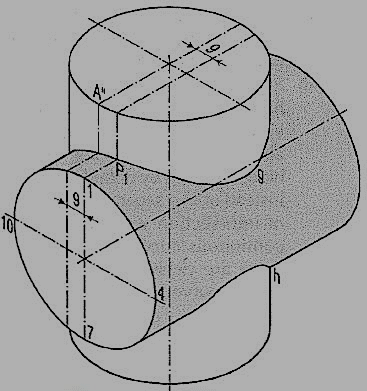
Figure 5
(i) Draw the three views and project points of intersection of lines which lie within the vertical cylinder.
(ii) Locate key points e' and f' as shown in problem 1. In addition to these, mark two more key points g and h (in the side view) where the circle cuts the extreme line b"b" of the vertical cylinder.
(iii) Project these points to g' and h' on the line b'b' in the front view. Draw a curve through all the points, showing the hidden portion by dotted lines. Instead of two separate curves of intersection we have one continuous curve. Note that there are twelve key points in this curve (fig. 6).
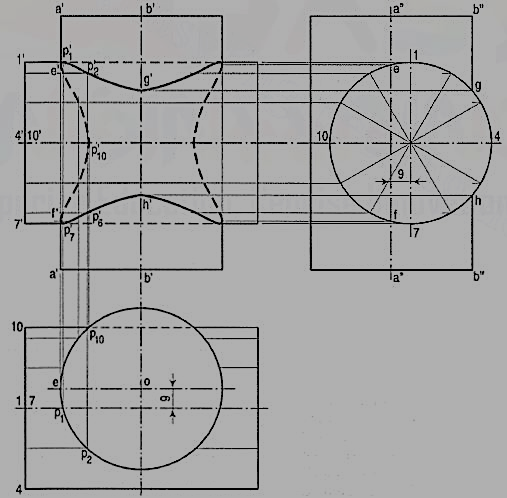
Figure 6
Intersection of cylinder and prism:
Problem:
1. A vertical cylinder of 60 mm diameter has a square hole of 30 mm sides cut through it. The axis of the hole is horizontal, parallel to the V.P. And 6 mm away from the axis of the cylinder. The faces of the hole are equally inclined to the H.P. And the V.P. Draw the projections of the cylinder showing the hole in it.
(i)Draw three views of the cylinder showing the lines for the hole in given position. Project all the key points, i.e. points of intersection of the edges of the hole with the surface of the cylinder, viz. p'1,p'2 etc. and those of the extreme lines of the cylinder with the surfaces of the hole, viz. e', fetch. Project a few intermediate points also (fig. 7).
(ii) Draw the required curve through these points on both sides of the axis. Note that the back portion of the hole is also visible. The curves from p'1 toe' and p'3 to fend in opposite directions.
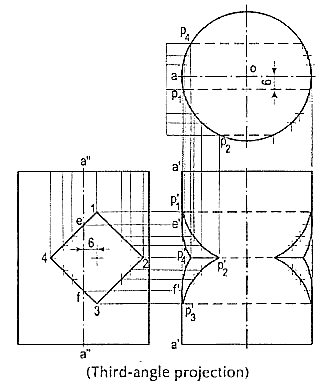
Figure 7
2. A vertical cylinder of 60 mm diameter is penetrated by a horizontal square prism, base 40 mm side, the axis of which is parallel to the V.P. And 10 mm away from the axis of the cylinder. A face of the prism makes an angle of 30° with the H.P. Draw their projections, showing curves of intersection.
(i) Draw the views in the required position. One longer edge of the prism will remain outside the cylinder. Project all the key points, viz. Points of intersection of the edges of the prism with the cylinder and those of the extreme lines of the cylinder with the surface of the prism, as shown in the figure.
(ii) To obtain accurate shape of the curves, project few more intermediate points also. These are omitted from the figure. Draw the required curve of intersection through these points, taking precaution to show the hidden part by dashed lines.
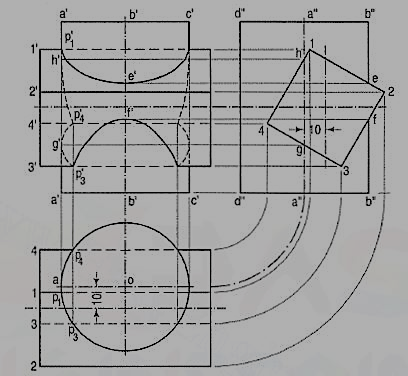
Figure 8
3. (fig.9): A connecting rod, 50 mm diameter, has a rectangular block 65 mm wide and 25 mm thick, forged at its end. The rod joins the block with a turned radius of 25 mm. Draw the projections of the rod showing curve of intersection.
The rod increases in diameter as it approaches the block. This forms what is called a fillet of 25 mm radius. As the width of the block is not as large as the biggest diameter of the rod, a curve of intersection is formed. Points on the curve are found as shown in fig. 9.
(i) Assume a horizontal cutting plane passing through a line, say a'a'. The section of the rod is a circle (see the top view) which cuts the sides of the block at points b.
(ii) Project these points to points b' on the line a'a'. Then the points b' lie on the curve. Obtain more points by assuming additional sections. The highest point on the curve will be on the line where the diameter of the section of the rod is equal to the width of the block.
Fig. 10 shows the shape of the curve when the diameter of the rod is equal to the width of the block. In this case, the highest point on the curve is on the horizontal line through the centre of the arc for the fillet.
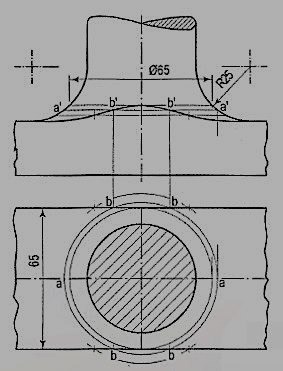
Figure 9
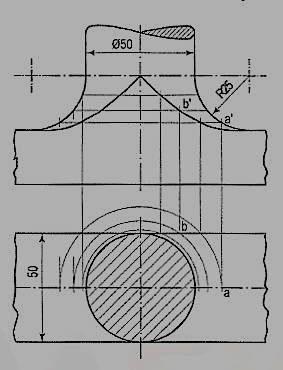
Figure 10
Intersection of cone and cylinder
Problem:
1.A vertical cone, diameter of base 75 mm and axis 100 mm Jong, is completely penetrated by a cylinder of 45 mm diameter. The axis of the cylinder is parallel to the H.P. And the V.P. And intersects the axis of the cone at a point 28 mm above the base. Draw the projections of the solids showing curves of intersection.
(a) Cutting-plane method (fig. 11 and fig. 12):
(i) Draw lines dividing the surface of the cylinder into twelve equal parts.
(ii) Assume a horizontal cutting plane passing through say, point 2 (fig. 11).The section of the cylinder will be a rectangle of width w (i.e. the line 2-12),while that of the cone will be a circle of diameter ee. These two sections intersect at points p2 and p12. These sections are clearly indicated in the top view by the rectangle 2-2-12-12 and the circle of diameter ee (fig. 12).
In the front view, the cutting plane is seen as a line coinciding with 2'2'. Points p2and p12 when projected on the line 2' 2'(with which the line 12'-12' coincides) will give a point p'2 (with which p'12 will coincide). Then p'2 and p'12 are the points on the curve of intersection.
(iii) To obtain the points systematically, draw circles with centre o and diameters dd,ee, ff etc. cutting lines through 1, 2 and12, 3 and 11 etc. at points p1, p2 andP12, P3 and P11 etc.
(iv) Project these points to the corresponding lines in the front view. Two more key points at which the curve changes direction must also be located. Their positions are determined from the side view. They are the points of nearest approach viz. m" and n" at which, lines drawn from the centre of the circle (i.e. the axis of the cylinder) and perpendicular to the extreme generators of the cone, cut the circle.
(v) Project these points to m' and n' in the front view and to m and n in the top view on the corresponding lines. Draw curves through these points in both the views. The back curve in the front view will coincide with the front curve. In. The top view a part of the curve will lie hidden and hence, it will be dotted. Draw similar curves on the right-hand side of the axis of the cone.
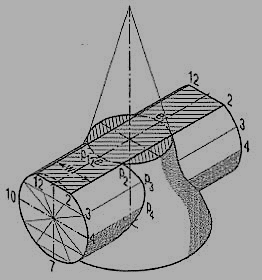
Figure 11
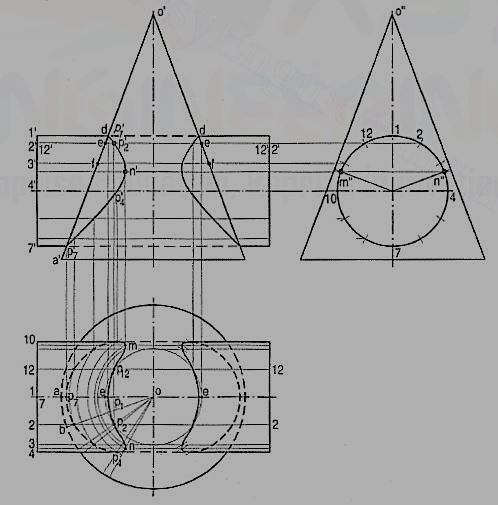
Figure 12
(b) Line method (fig. 13): The surface of the cylinder is a circle in the side view.
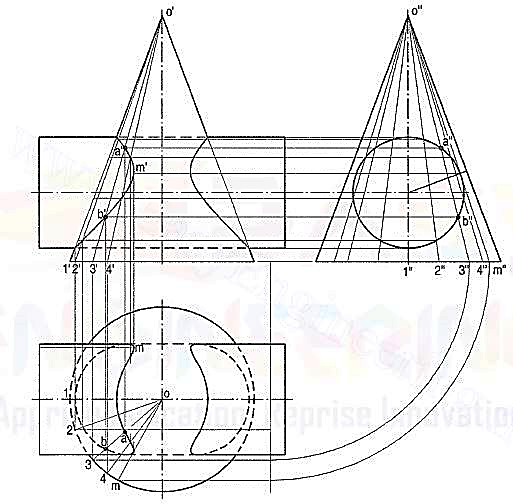
Figure 13
(i) Hence, draw a number of lines (representing generators of the cone) o‘’1’’ o’’2" etc. in the region of the circle and symmetrical on both sides of the axis. Points where these lines intersect the circle, lie on the curve of intersection.
(ii) To project them in the front and top views, first project the lines in both the views and then, locate the positions of these points on them. Let us take the line o"3" in the side view. Locate its position o3 in the top view as shown and project its front view o'3'. Project points a" and b" to points a' and b' on o'3' and from there, to a and b on o3.
(iii) Project all points in the same manner and draw the required curves through them. This method is a type of cutting-plane method in which cutting planes pass through the apex and are parallel to the axis of the cylinder.
Problem:
1. A vertical cone, base 80 mm diameter, axis 100 mm long, is penetrated by a horizontal cylinder of 40 mm diameter, the axis of which is 25 mm above the base of the cone, parallel to the V.P. And 6 mm away from the axis of the cone. Draw the projections, showing curves of intersection.
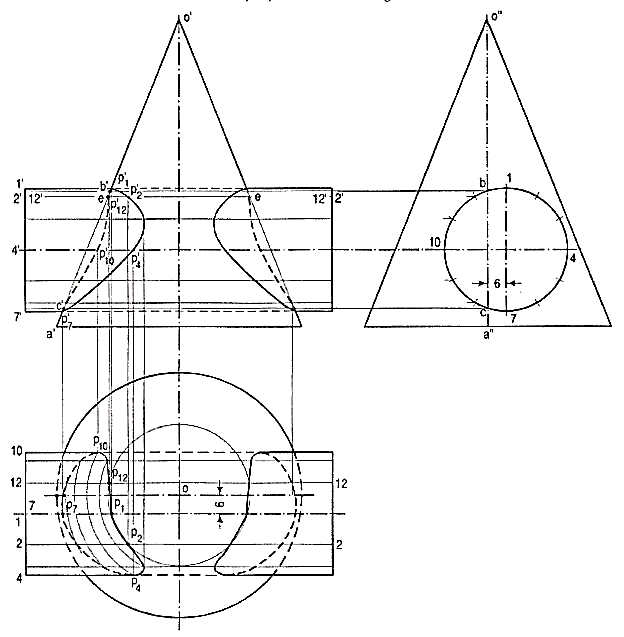
Figure 14
Draw the three views of the solids.
(i) Assuming a horizontal cutting plane through the line 2'2', draw a circle in the top view with centre o and diameter ee, cutting lines 2-2 and 12-12 at pointsP2 and P12.
(ii) Project these points to p'2 and p'12 on the line 2'2' (with which 12'-12'coincides). Obtain other points and the key points b' and c' in the same manner and draw the curves as shown. As the axes do not intersect, the back curves in the front view are different from the front curves.
2. A vertical cone, diameter of base 75 mm and axis 90 mm long is penetrated by a cylinder of 50 mm diameter, the axis of which is parallel to and 10 mm away from that of the cone. Draw the projections showing curves of intersection, when (i) the plane containing the two axes is parallel to the V.P.; (ii) the plane containing the two axes is inclined at 45° to the V.P.
(i) Draw the projections (fig. 16-30). The centre of the circle for the cylinder (in the top view) will lie on the horizontal centre line and 10 mm away from the centre of the circle for the cone. Divide the base-circle of the cone into twelve equal parts and draw twelve generators in both the views. The surface of the cylinder is seen as a circle in the top view. It cuts the lines on the surface of the cone at points p 1, p2 etc. Project these points to p'1, p'2 etc. on the corresponding lines in the front view. Draw the required curve of intersection through these points. The curve at the back will coincide with the front curve.
The cutting-plane method is exactly similar. Assume a series of vertical cutting planes passing through the apex. The sections of the cone will be triangles and those of the cylinder will be rectangles. Points of intersection between these sections will lie on the curve. For example, take a cutting plane coinciding with the line 2-8. In the front view, the section of the cone will be shown by triangle o'-2'-8', while that of the cylinder will be a rectangle of width w. Points p'2 and p'8 at which lines o'2' and 0‘8‘cutthe sides of the rectangle, lie on the curve of intersection.
Intersection of cone and prism:
Problem:
(fig. 15) Draw an equilateral triangle of 100 mm side with one side horizontal. Draw a square of 35 mm side in its centre with its sides inclined at 45° to the base of the triangle. The figure shows the front view of a cone standing on its base on the ground and having a square hole cut through it. Draw three views of the cone.
(i) Project the top and side views from the given view. Assume the cone as cut by a horizontal cutting plane passing through points a'. The section of the cone will be a circle of diameter bb. The hole will be cut in two straight lines through points a' and perpendicular to the V.P.
(ii) Therefore, with centre o (the apex in the top view) and diameter bb, draw circle cutting the projectors through a' at points a. Assume additional cutting planes, particularly those which pass through corners of the square and find other points. Draw curves through these points.
The method of locating points a" in the side view is clearly indicated by construction lines. Obtain all points in the same manner.
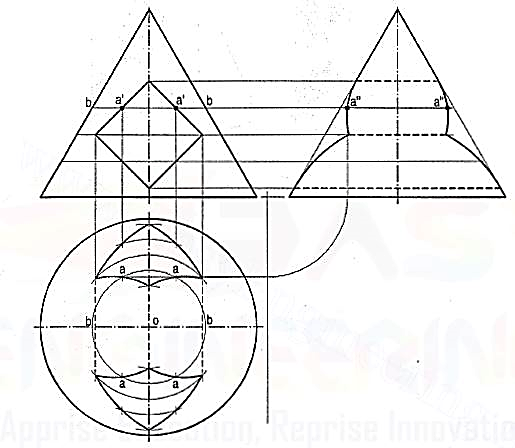
Figure 15
Intersection of Cone and Cone:
Problem:
1. A vertical cone, base 90 mm diameter and axis 90 mm long, is penetrated by another cone of base 75 mm diameter and height 100 mm. The axes of the two cones bisect each other at right-angles. Draw the front view showing curves of intersection, when the axis of the penetrating cone is parallel to the V.P. (fig. 16)
(i) Assume a horizontal cutting plane coinciding with a line a'd'. The section of the vertical cone will be a circle of diameter ee. The section of the horizontal cone will be a hyperbola. The width of the hyperbola at the point a' will be equal to twice the length of the line a'1'; that at the point b' will be twice b'2' etc.
(ii) In the top view, mark points on the projector through a' and symmetrical on both sides of the horizontal axis, so that 1-1 = twice a'1 '. Similarly, mark points on the projector through b' so that 2-2 = twice b'2' etc. Draw the hyperbola through the points thus obtained.
(iii) Draw a circle with centre o and radius c'e', cutting the hyperbola at points p1and q1. Project p1to p'1 and q1 to q'1 on the cutting-plane line a'd'.

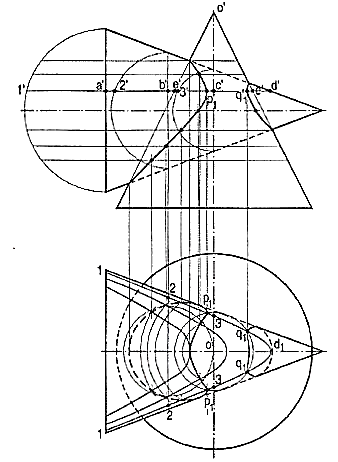
Figure 16
Then p1, q1, p'1 and q'1 are the points on the curves in the two views. Similarly, assume additional sections, preferably at equal distances on both sides of the axis (so that the sections will be the same). Draw the hyperbolas and circles in the top view and determine the points of intersection. Draw curves in both the views and on both sides of the vertical axis. The curves can be determined in the same manner even when the axes do not intersect.
Intersection of Sphere and Cylinder or Prism:
Problem:
1. (fig. 17) A hole of 50 mm diameter is drilled through a sphere of 75 mm diameter. The axis of the hole is 70 mm away from the centre of the sphere. Draw three views of the sphere when a vertical plane containing the centre of the sphere and the axis of the hole is inclined at 60° to the V.P.
(i) Draw the top view of the sphere and show the circle for the hole in the required position.
(ii) Project the front view and the side view. Divide the circle for the hole into twelve equal parts.
(iii) Assume many cutting planes parallel to the V.P. The sections of the sphere will be circles, while the hole will be cut in straight lines. Intersection of the circles with corresponding lines will give points on the curves.
(iv) Let us take a section plane passing through points 3 and 5. The section of the sphere will be a circle of diameter aa. The lines through 3 and 5 intersect this circle at points 3' and 5' which lie on the curve. Obtain the twelve points in the same manner. Also plot the key points at which the section through the centre of the sphere is cut by the lines of the hole. Draw curves through all the points. Project the points on the side view horizontally from the front view on corresponding lines of the hole and draw curves through them.
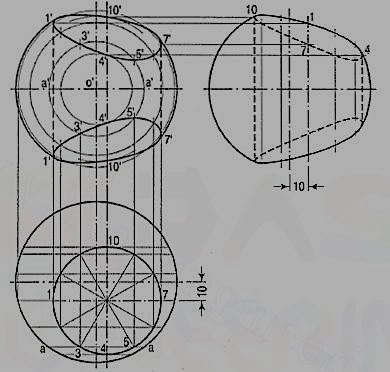
Figure 17
2. A sphere of 80 mm diameter is penetrated by a square prism, base 45 mm side, the axis of which passes through its centre. Draw the front view of the solids showing curves of intersection when the axis of the prism is parallel to both the planes and the faces are equally inclined to the V.P.
(i) Draw the front view and project the side view. Assume a vertical cutting plane passing through, say points a. The section of the sphere will be a circle of diameter bb. It is cut by the section of the prism (a rectangle of width aa) at points an' as shown in the front view. Then points a' are on the curve of intersection.
(ii) Obtain more points together with the key points in the same manner and draw curves through them.
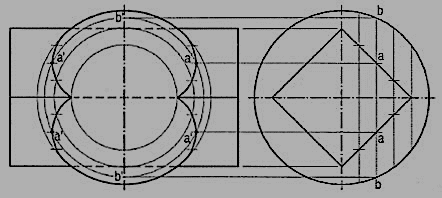
Figure 18
Exercise:
1. A vertical square prism, base 50 mm side has its faces equally inclined to theV.P. It is completely penetrated by another square prism of base 30 mm side, the axis of which is parallel to both the planes and is 6 mm away from the axis of the vertical prism. The faces of the horizontal prism also are equally inclined to the V.P. Draw the projections of the solids showing lines of intersection.
2. Two equal prisms whose ends are equilateral triangles of 40 mm side and axes 100 mm long, intersect at right angles. One face of each prism is on the ground. The axis of one of the prisms makes 30° with the V.P. Draw three views of the solids.
3. A square prism of base 50 mm side and height 125 mm stands on the ground with a side of the base inclined at 30° to the V.P. It is penetrated by a cylinder, 50 mm diameter and 125 mm long, whose axis is parallel to both the H.P. And the V.P. And bisects the axis of the prism. Draw the projections showing fully the curves of intersection.
References:
1. Engineering Drawing N.D. Bhatt / Charotar
2. Engineering Drawing / N. S. Parthasarathy and Vela Murali/ Oxford
3. Engineering Drawing / Basant Agrawal and McAgrawal/ McGraw Hill
4. Engineering Drawing/ M. B. Shah, B.C. Rane / Pearson.
5. Computer Aided Engineering Drawing – K Balaveera Reddy et al – CBS Publishers