Unit – 4

Torsion, stresses and deformation in circular and hollow shafts

4.1 Torsion

Torsion equation or torsion constant is defined as the geometrical property of a bar’s cross-section that is involved in the axis of the bar that has a relationship between the angle of twist and applied torque whose SI unit is m4. The torsion equation is given as follows:

T/J= τ/r=Gθ/L

Torsion equation derivation

Following are the assumptions made for the derivation of torsion equation:

• The material is homogeneous (elastic property throughout)
• The material should follow Hook’s law
• The material should have shear stress proportional to shear strain
• The cross-sectional area should be plane
• The circular section should be circular
• Every diameter of the material should rotate through the same angle
• The stress of the material should not exceed the elastic limit

Consider a solid circular shaft with radius R that is subjected to a torque T at one end and the other end under the same torque.

T = Maximum twisting torque or twisting moment

D = Diameter of shaft

R = Radius of shaft

J = Polar moment of Inertia

τ= Maximum Permissible Shear stress (Fixed for given material)

G = Modulus of rigidity

θ= Angle of twist (Radians) = angle D'OD L  = Length of shaft.

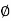= Angle D'CD = Angle of Shear strain 

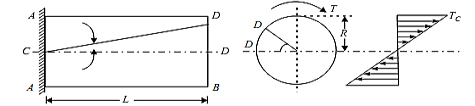
Fig.1

Then Torsion equation is: T/J =   τ/R = G. θ /L

Let the shaft is subjected to a torque or twisting moment 'T'. And hence every C.S. Of this shaft will be subjected to shear stress.

Now distortion at the outer surface = DD'

Shear strain at outer surface = Distortion/Unit length tan  θ = DD'/CD

i.e. shear stress at the outer surface (tan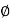=) = DD'/L or = DD'/L           ...(i)

Now DD' = R.θ              or      =  R .θ /L    ...(ii)

Now G = Shear stress induced/shear strain produced

G = τ / (R. θ /L);

Or;     τ/R = G. θ /L            …..(A);

This equation is called Stiffness equation.

Hear G, θ , L are constant for a given torque 'T'. That is proportional to R

If τ r  be the intensity of shear stress at any layer at a distance 'r' from canter of the shaft, then;

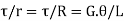
Now Torque in terms of Polar Moment of Inertia

From the fig

Area of the ring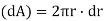

Since,

Turning force on Elementary Ring; .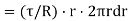

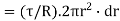
Turning moment 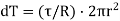.dr.r

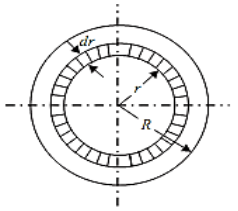
Fig.2

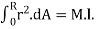of elementary ring about an axis perpendicular to the plane passing through center of circle.

Polar Moment of Inertia

Now from equation (ii) T = (τ/R)  J

Or                                       τ/R = T/J;                           ..(B)

This equation is called as strength equation

The combined equation A and B; we get

T/J =   τ/R = G. θ /L            

This equation is called as Torsion equation.

From the relation             T/J =   τ/R

We have  

T =   τ .J/R = τ .ZP

For the given shaft IP and R are constants and IP/R is thus constant and is called as polar modulus (ZP) of the shaft section.

Polar modulus of section is thus measure of strength of shaft in the torsion.

Torsional rigidity or Torsional Stiffness (K): = G.J/L = T/θ

Key takeaways

1) Torsional rigidity or Torsional Stiffness (K): = G.J/L = T/θ

2) Torsion equation is: T/J =   τ/R = G. θ /L

4.2 Stresses and deformation in circular in circular and hollow shafts

Consider a bar or shaft of circular cross section twisted by a couple T, assume the left-hand end is fixed and the right-hand end will rotate a small angle ϕ, called angle of twist if every cross section has the same radius and subjected to the same torque, the angle ϕ (x) will vary linearly between ends under twisting deformation, it is assumed

1. Plane section remains plane

2. Radii remaining straight and the cross sections remaining plane and circular

3. If ϕ is small, neither the length L nor its radius will change consider an element of the bar dx, on its outer surface we choose a small element abcd,

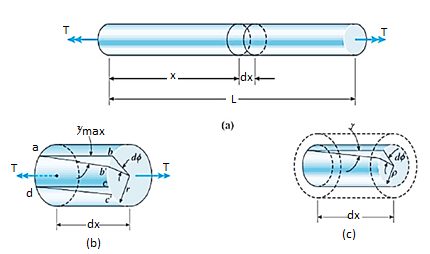
Fig. 3

During twisting the element rotate a small angle d, the element is in a state of pure shear, and deformed into ab'c'd, its shear strain γmax is

γmax = bb’/ab = r d ϕ / dx

d ϕ / dx represents the rate of change of the angle of twist ϕ, denote θ= d ϕ / dx as the angle of twist per unit length or the rate of twist, then γmax = r θ in general, ϕ and θ are function of x, in the special case of pure torsion, θ is constant along the length (every cross section is subjected to the same torque) θ = ϕ/L and γmax = rθ/L and the shear strain inside the bar can be obtained

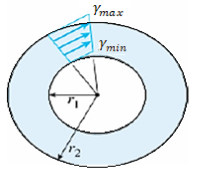
Fig. 4

γ = ρ.θ=ρ. γmax / r

γmin = r1 /r2 γmax

For a circular tube, it can be obtained. The above relationships are based only upon geometric concepts, they are valid for a circular bar of any material, elastic or inelastic, linear or nonlinear.

4.3 Stepped shafts

A shaft which tapers in a series of steps rather than one continuous narrowing. The stepped shaft was introduced by the True-Temper Division of The American Fork and Hoe Company which initially manufactured shafts with a smooth taper from butt to tip.

4.4 Deflection of shafts fixed at both the ends

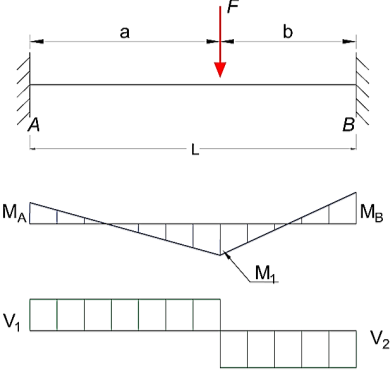
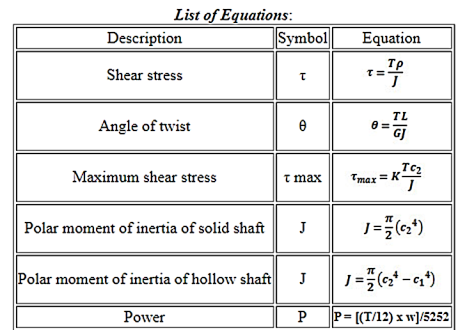
Fig 5 Beam Fixed at Both Ends - Single Point Load

Bending Moment

MA = - F a b2 / L2                               (1a)

Where

MA = moment at the fixed end A (Nm, lbf ft)

F = load (N, lbf)

MB = - F a2 b / L2                              (1b)

Where,

MB = moment at the fixed end B (Nm, lbf ft)

MF = 2 F a2 b2 / L3                           (1c)

Where,

MF = moment at the point load (Nm, lbf ft)

Deflection

δF = F a3 b3 / (3 L3 E I)                                  (1d)

Where,

δF = deflection at point load (m, ft)

E = Modulus of Elasticity (Pa (N/m2), N/mm2, psi)

I = Area Moment of Inertia (m4, mm4, in4)

Support Reactions

RA = F (3 a + b) b2 / L3                                 (1f)

Where

RA = support force at fixed end A (N, lbf)

RB = F (a + 3 b) a2 / L3                                 (1g)

Where

RB = support force at fixed end B  (N, lbf)

4.5 Stresses and deflection of helical springs

Springs are energy absorbing units whose function is to store energy and to restore it slowly or rapidly depending on the particular application.

Fig 6. Spring

A spring may be defined as an elastic member whose primary function is to deflect or distort under the action of applied load; it recovers its original shape when load is released.

Helical spring: They are made of wire coiled into a helical form, the load being applied along the axis of the helix. In these type of springs the major stresses is torsional shear stress due to twisting. They are both used in tension and compression.

Helical springs are used in various applications due to their shock absorption and load bearing properties. So, it is important to calculate its load bearing capacity, if you are selecting a helical spring for an application. This post discusses two types of helical springs that are differentiated on the basis of their load bearing capacity.

Types of Helical Springs on the Basis of Load Bearing Capacity

The load bearing capacity depends on various factors such as total number of coils, coil gaps, wire shapes, etc. The below mentioned are the two types of helical springs distinguished on the basis of their coils.

1. Open Coiled Helical Springs: These helical springs are designed to resist compression, which is they are known as compression springs. These springs are not wound tightly, and have a high pitch. This results in large spaces between the coils, which also makes the springs very recognizable. Hence, no two turns of a spring will lie on the same axis of the helix. The turns of these springs are located at inclined angles towards the helical axis. Some typical applications include ball point pens, valve assemblies in engines, car suspension systems, pogo sticks, etc.

CLOSE COILED HELICAL SPRING-UNDER AXIAL FORCE

This spring is subjected to either axial load or axial couple.

The parameters to be studied in springs are stress, stiffness and resilience.

Symbols used

Do= outer coil diameter

Di= inside coil diameter

Dm= mean coil diameter = D

d=diameter of wire

na = number of active turns (circles) in the spring

ni = Number of inactive turns

C = spring index= D/d  

(normally 4 to 12)

k = Wahl’s Stress concentration factor

ԏ = shear stress in spring wire

ϴ = angle of twist in wire

L= length of wire

T = torque= W x R

CLOSED COILED HELICAL SPRINGS – AXIAL LOAD

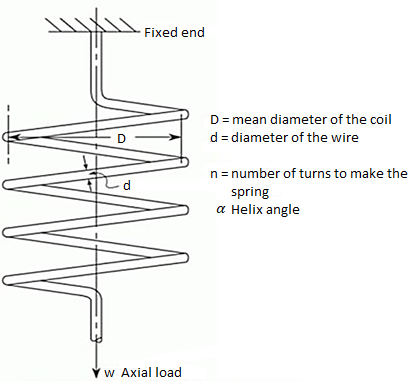
Fig 7. Closed coiled helical spring under axis load W

As the helix angle (angle of the turn with the horizontal) is small, axial load only causes twist in the wire of the spring. It is similar to a shaft under pure torsion. It is considered only in pure torsion and the torsion equation is used to analyze it.

Actually stresses present will be

• Torsion shear stress
• Bending stress
• Direct shear stress

Bending stress and direct shear stresses have been found to be negligible. However their small effect has been accounted for by Wahl stress concentration factor.

T = W x R=WxD/2

T/J = ԏ/r = Gϴ/L

J = (π/64)d4

R =radius of wire = d/2

G = Modulus of rigidity

ϴ= Angle of twist in radians

L= length of wire = 2πrn

Using T/J = ԏ /r

(WD/2)/ (π/64)d4 = ԏ /(d/2)

Α = angle of helix = 0 in a closed coil spring

Stress = ԏ= 8WD/πd3

Stress concentration factor accounts for two things

(i) Direct shear stress consideration

(ii) Stress concentration due to change in curvature

Wahl’s stress concentration factor is given by

K = (4C-1)/(4C-4)+ 0.615/C

Where C is spring index=D/d

Now actual shear stress becomes = kԏ= k 8WD/πd3  

(1/2)W δ = (1/2) Tϴ,

δ = 64 WR3n/Gd4                                                 

Stiffness = k= W/δ = Gd4/64R3n                     

Resilience = u = ԏ2/2G       

Solid length = nd  

References:

1. U.S. Department of Energy, Material Science. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
2. Elements of Strength of Materials (Timoshenko)
3. Strength of Materials (S. Ramamrutham)
4. A Textbook Of Strength Of Materials (R K Bansal)
5. Strength of Materials (Dr B.C.Punmia)