Unit - 4
Electrical Machines
The fundamental principle of induction machine is the creation of rotating and sinusoidally distributed magnetic field in the air gap. Three phase balanced power supply is fed to the three-phase stator winding creates a synchronously rotating magnetic field. Due to relative speed between rotating flux and stationary conductors, an emf is induced. The frequency to induced emf is same as supply frequency.
As shown in below fig.a , the stator field is assumed to clockwise. The relative motion of rotor w.r.t stator is anticlockwise. From Right-hand rule, the direction of induced emf in rotor is outwards. By the effect of combined field as shown in fig b the rotor experiences a force tending to rotate it in clockwise direction. Hence rotor rotates in the same direction as the stator field.
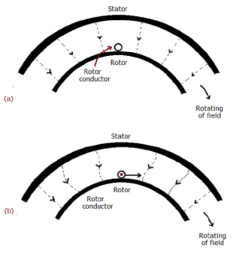
Fig 1 Rotating Magnetic Field
The speed of this rotating field is called synchronous speed. If the rotor is initially stationary, its conductors will be subjected to a changing magnetic field, inducing current in the short-circuited rotor at the same frequency. The interaction of air gap flux and rotor mmf produces torque. At synchronous speed rotor cannot have any torque.
There are two main parts of induction motor:
a) Stator
b) Rotor
a) Stator:
It is stationary part of induction motor. It has number of stampings. It is wound with three phase winding which is fed from 3-phase supply. The number of poles here are defined, they are selected according to the speed required. If required speed is greater than we need less number of poles. The stator produces an alternating flux when fed with 3-phase supply which revolves with synchronous speed(Ns = 120f / P). The synchronous speed is inversely proportional to number of poles.
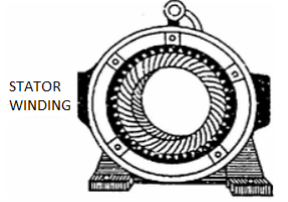
Fig:2 Stator
b) Rotor: It is rotating part of induction motor. There are two types of rotor
i)Squirrel cage rotor:
The rotor consists of a cylindrical core with parallel slots for carrying the rotor conductor. Each slot has one copper or aluminium bar. Each end of all bars is joined with metal ring. The entire construction resembles a squirrel cage. The rotor is not connected electrically to the supply it has induced current from stator. Almost 90% of induction motors are squirrel cage type. But is has a disadvantage of low starting torque, because the rotor bars are permanently short-circuited.
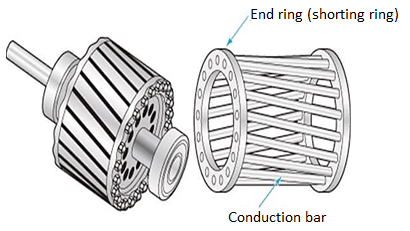
Fig 3 Squirrel cage rotor
Ii) Phase-wound rotor: It has laminated cylindrical core and the windings are uniformly distributed in the slots which are usually star connected. The other three winding terminals are brought out and connected to three insulated slip rings mounted on shaft with brushes resting on them. The three brushes are connected to a 3-phase star-connected rheostat as shown in Figure below.
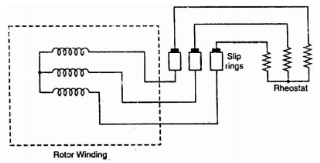
Fig 4: 3-phase star connected
At starting, the external resistances are included in the rotor circuit to give a large starting torque. These resistances are gradually reduced to zero as the motor runs up to speed. The external resistances are used during starting period only. When the motor attains normal speed, the three brushes are short-circuited so that the wound rotor runs like a squirrel cage rotor.
Slip:
The rotor can never have same speed as that of stator. If it occurs then there will not be relative speed between the two, hence no rotor emf, no rotor current and so no torque to maintain rotation. Due to this reason speed of rotor is always less than the stator field. The difference between the synchronous speed Ns and the actual speed N of the rotor is called as slip.
% slip s=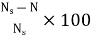
Therefore, rotor speed N=Ns(1-s).
Frequency of rotor current:
When rotor is stationary its frequency is same as the supply frequency. But when rotor revolves its frequency depends upon the slip-speed. Let frequency of rotor current be f’
Ns-N=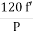
But Ns=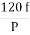
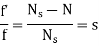
Rotor current have same frequency
=
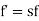
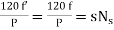
MMF produced by rotor current:
a) For standstill condition:
Let E2=emf induced per phase of rotor at standstill
R2=resistance per phase of rotor.
X2=reactance per phase of rotor at standstill=2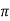
f1L2
Z2=rotor impedance per phase
I2=rotor current per phase
Z2=R2+jX2
=
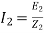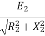
Power Factor cosφ2=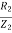
=
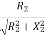
b) Rotor current at slip s:
Induced emf per phase in rotor winding at slip s is E2s=sE2
Rotor winding reactance per phase at slip s will be X2s=2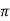
f2L=sX2
Rotor winding impedance per phase at slip s is Z2s=R2+jX2s=R2+jsX2
Rotor current at slip s, I2s=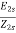
Power factor at slip s is cosφ2s=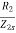
Key takeaway
Ns-N=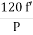
But Ns=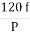
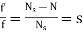
Examples
Que) The stator of a 3-phase induction motor has 5 slots per pole per phase. If supply frequency is 50Hz. Calculate a) number of stator poles produced and total number of slots in stator. b) Speed of rotating stator flux.?
Sol: a) P=2n=2*5=10 poles
Total number of slots= 5 slots/pole/phase * 10 poles * 3 phase=150
b) Ns=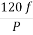
=120x50/10=600rpm
Que) A 3-phase induction motor is wound for 5 poles and is supplied from 50 Hz. Calculate a) synchronous speed b) rotor speed when slip is 4% c) rotor frequency when rotor runs at 500 rpm?
Sol: a) Ns=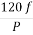
=120x50/5=1200 rpm
b) rotor speed N=Ns(1-s)=1200(1-0.04)=1152 rpm
c) when rotor speed is 500 rpm, slip s=(Ns-N)/Ns=(1200-500)/1200=0.58
Rotor current frequency f’=sf=0.58x50=29.17 Hz
Que) A 3-phase, 50 Hz,3-pole induction motor has a slip of 4%. Calculate a)speed of rotor. B) frequency of rotor emf. If the rotor as a resistance of 2ohm, and standstill reactance of 4ohm, calculate the power factor c)at standstill and d)at a speed of 1200rpm?
Sol: Ns=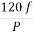
=120x50/3=2000 rpm
a) Speed of rotor N=Ns(1-s)=2000(1-0.04)=1920 rpm
b) Frequency or rotor = f’=sf=0.04x50=2Hz
R2=2ohm, X2=4ohm
Z2=R2+jX2=2+j4=4.47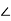
63.43o ohm
c) Power factor cosφ2=0.44(lag)
Slip at speed 1200rpm s=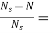
2000-1200/2000=0.4
Rotor impedance at slip s=0.4 is
Z2s=R2+jsX2=2+jx0.4x4=2.56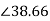
oohm
Power factor at 1200rpm is cosφ2s=cos38.66o=0.78(lag)
Q) A 3-phase induction motor star connected rotor has an induced emf of 70volts between slip rings at standstill on open circuit. The rotor has a resistance and reactance per phase of 1ohm and 5ohm respectively. Calculate current/phase and power factor when slip rings are short circuited?
Sol: Standstill emf/rotor phase=70/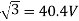
Rotor impedance/phase=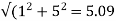
ohm
Rotor current/phase=40.4/5.09=7.92A
Power factor cosφ=0.99
Que) A 3-phase induction motor star connected rotor has an induced emf of 70volts between slip rings at standstill on open circuit. The rotor has a resistance and reactance per phase of 1ohm and 5ohm respectively. Calculate
Current/phase and power factor when slip rings are connected to star connected rheostat of 2ohm?
Sol: Rotor resistance/phase=2+1=3 ohm
Rotor impedance/phase=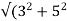
=5.83 ohm
Rotor current/phase=(70/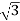
)/5.83=6.93A
Cosφ=3/5.83=0.514
Que) A 6-pole, 3-phase induction motor operates from a supply whose frequency is 50Hz. Calculate i) speed at which the magnetic field of stator is rotating. Ii)speed of rotor when slip is 4%. Iii)frequency of rotor current when slip is 3%?
Sol: i) Stator revolves at synchronous speed. So, Ns=120f/P=120 x 50/6=1000rpm
Ii)rotor speed N=(1-s)Ns=(1-0.04) x 1000=960rpm
Iii)frequency of rotor current f’=sf=0.03 x 50=90rpm
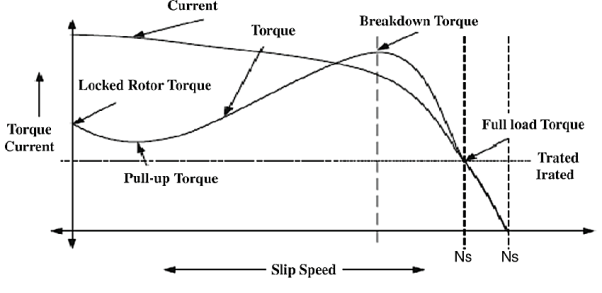
The below curve can be divided into three regions.
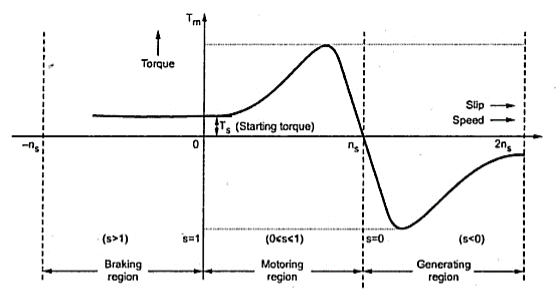
Fig:5 Torque-Slip Characteristics
i)Motoring Region(0≤s≤1): The induction motor rotates in the same direction as that of the field. Here the speed decreases and torque increases till breakdown torque is reached. In this region air-gap flux is nearly constant. After breakdown torque Tmax , torque decreases and slip increases.
Ii)Generating Region(s<0): In this machine operates as a generator. The rotor rotates at a speed greater than synchronous speed in same direction as that of rotating magnetic field. Due to super synchronous speed the slip becomes negative and creates negative regenerative torque.
Iii)Plugging Region(1≤s≤2): Here slip becomes greater than unity. So, motor rotates in the opposite direction of the rotating magnetic field. Here the stator field is reversed by changing the phase sequence of input supply, due to this the direction of rotating magnetic field also changes. Here torque is positive but speed is negative. So, plugging torque appears as breaking torque. This method of breaking is called plugging.
In general, we can categorise losses as:
i)Constant losses: They remain constant over the normal working range of induction motor. By no-load test we can find these losses. The losses falling in this category are Iron or core loss, Mechanical Loss and Brush Friction loss.
a) Iron or core loss: The core losses depend on the frequency of supply voltage. As the frequency of rotor is always less than that of stator. Hence, core loss in rotor is less compared to that of stator. The core loss can be further classified as hysteresis and eddy current losses.
b) Mechanical and Brush Friction Loss: These are low at starting and increases with increase in speed. In induction motor speed is usually constant hence these losses also remain constant. Mechanical losses occur in bearings and brush friction losses occur in wound rotor induction motor.
Ii)Variable losses: These losses occur due to current flowing in stator and rotor windings. As the load changes, the current flowing in rotor and stator winding also changes and hence these losses also change. Therefore, these losses are called variable losses. The copper losses are obtained by performing blocked rotor test on three phase induction motor.
Efficiency
Rotor Efficiency=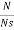
=
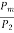
3-phase induction moor efficiency=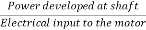
=
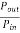
Que) The power input to a rotor of 440V, 50Hz, 6-pole, 3-phase, induction motor is 60kW. The rotor force is observed to make 80 alterations per minute. Calculate i) slip ii) rotor speed iii) rotor cu loss per phase?
Sol: 80 alterations per minute=80/60 cycles per second=1.333Hz=sf
i)slip=1.333/50=0.027 P.u.=2.7%
Ii)Rotor speed N=(1-s) Ns=(1-0.027) x 1000=973.33rpm
Ns=120f/P=120 x 50/6=1000rpm
Iii)rotor cu loss/phase=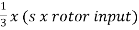
=
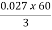=0.54kW
Que) The power input to a 3-phase induction motor is 80kW. The stator loss is total 1kW. Find the mechanical power developed and the rotor cu loss per phase if the slip is 3%?
Sol: P2= stator input – stator losses=80-1=79kW
Pm=(1-s)P2==(1-0.03) x 79=76.63kW
Total rotor cu loss=sP2=0.03 x 79=2.37kW
Rotor cu loss per phase=2.37x1000/3=790W
Que) The power input to a rotor of a 400V, 50hz,6-pole, 3-phaseinduction motor is 15kW. The slip is 4%. Calculate i) frequency of rotor current. i)rotor speed. Iii)rotor cu loss iv) rotor resistance/phase if rotor current is 50A?
Sol: i) frequency of rotor current=sf=0.04 x 50=2Hz
Ii) Rotor speed N=(1-s) Ns=(1-0.04) x 1000=960rpm
Ns=120f/P=120 x 50/6=1000rpm
Iii) rotor cu loss=s x rotor input=0.04 x 15=0.6kW
Iv)rotor cu loss/phase=0.6 x 1000/3=200W
602R2=200
R2=0.055Ω
Starting:
Direct on-line starter (Full voltage starting method)
In this induction motor is directly connected to the 3-phase supply. The DOL starter applies full line voltage to the motor terminals.
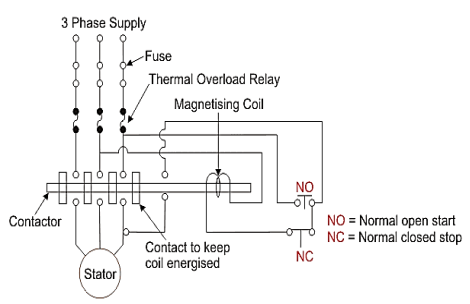
Fig:6 D.O.L Starter
If the high input current does not cause any excess voltage drop in circuit than only this starter can be used. The value of armature current in motor is given as
Ia=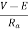
The expression for starting torque is given as
Ts starting torque
Tf Full load torque
If per phase rotor current at full load
Is per phase rotor current at starting
sf full load slip
ss starting slip
R2 rotor resistance
Ws synchronous speed of motor
In induction motor torque is given as
T=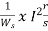
The ratio of starting torque to full load torque is given as
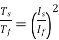x sf
The wiring diagram for a DOL starter is shown above. The working principle of a DOL starter begins with the connection to the 3-phase main with the motor. The control circuit is connected to any two phases and energized from them only. When we press the start button, the current flows through magnetizing coil and control circuit also.
The current energises the contactor coil and leads to close the contacts, and hence 3-phase supply becomes available to the motor. When we stop it, the current discontinues. As the supply to motor breaks the machine stops. The contactor coil (Magnetizing Coil) gets supply even though we release start button because when we release start button, it will get supply from the primary contacts as illustrated in the diagram of the Direct Online Starter.
The advantages of a DOL starter include:
- Simple and most economical starter.
- More comfortable to design, operate and control.
- Provides nearly full starting torque at starting.
- Easy to understand and troubleshoot.
- DOL starter connects the supply to the delta winding of the motor.
The reduced voltage starting methods are:
Star delta starter: The set up for star delta starter is shown below
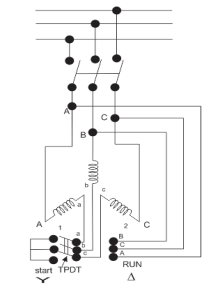
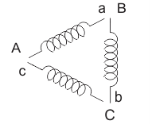
Fig:7 Star delta starter
The starter phases are connected to star by TPDT (triple pole double throw switch). Initially the TPDT switch is at position 1 and when motor attains steady state switch is thrown to position 2. In position 1 terminals are short circuited and at position 2 a, b and c are connected to B, C and A. The expression for starting torque is given as
Ts starting torque
Tf Full load torque
If per phase rotor current at full load
Is per phase rotor current at starting
sf full load slip
ss starting slip
R2 rotor resistance
Ws synchronous speed of motor
In induction motor torque is given as
T=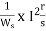
The ratio of starting torque to full load torque is given as
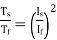x sf
Let V1 line voltage
Iss per phase starting current
Iss=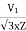
Starting current in stator when connected in delta position
Isd=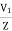
Isd=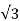
Iss
Then the torque ratio equation will be
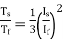x sf
This shows that the reduced voltage method has an advantage of reducing the starting current but the disadvantage is that all these methods of reduced voltage causes the objectionable reduction in the starting torque.
Speed Control: The speed can be controlled by the following methods.
i) Changing stator Pole: This can be done by Multiple stator windings. In stator two windings are provided which are isolated and have different number of poles. By switching we can control the supply to one winding and hence control the speed.
Ii) Supply voltage control: The torque produced is proportional to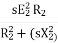 
. The value of 
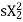is very small and R2 is also constant so T α
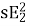. But E2α V therefore, T α sV2.This equation shows that if supply voltage is decreased the torque also decreases.
Iii) Adding rheostat in the stator: As we already know Tα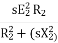
. The value of 
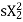is very small and E2 is also constant soTα
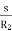. Now if we increase rotor resistance, R2 torque decreases but to supply the same load torque must remain constant. So, we increase slip, which will further result in the decrease in rotor speed. Thus, by adding additional resistance in the rotor circuit, we can decrease the speed of the three-phase induction motor.
Iv) v/f control: There is no direct relation in the speed and torque. At, full load the motor runs at a speed N. When mechanical load increases motor speed decreases till the motor torque again becomes equal to the load torque.
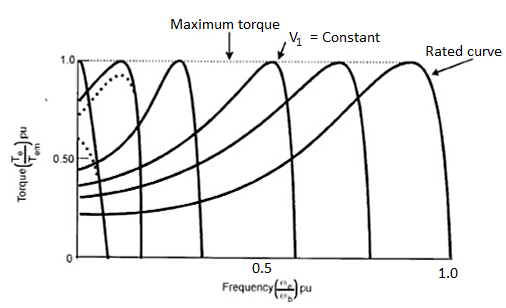
As long as two torques are equal the motor runs at constant speed. When the supply frequency increases the speed increases and reduces the maximum torque of motor. So,
i) F increases, N increases, Tmax decreases.
Ii) V increases, Tmax increases.
A Single-Phase Induction Motor consists of a single-phase winding which is mounted on the stator of the motor and a cage winding placed on the rotor. A pulsating magnetic field is produced, when the stator winding of the single-phase induction motor shown below is energized by a single-phase supply.
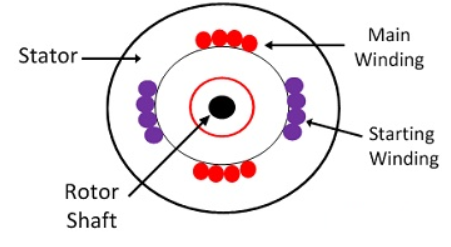
Fig 9 1-phase IM
The word Pulsating means that the field builds up in one direction falls to zero and then builds up in the opposite direction. Under these conditions, the rotor of an induction motor does not rotate. Hence, a single-phase induction motor is not self-starting. It requires some special starting means.
If the 1 phase stator winding is excited and the rotor of the motor is rotated by an auxiliary means and the starting device is then removed, the motor continues to rotate in the direction in which it is started.
The performance of the single-phase induction motor is analysed by the two theories. One is known as the Double Revolving Field Theory, and the other is Cross Field Theory. Both the theories are similar and explain the reason to produce torque when the rotor is rotating.
Working of 1-phase IM
Double Revolving Field Theory of Single- Phase Induction Motor
The double revolving field theory of a single- phase induction motor states that a pulsating magnetic field is resolved into two rotating magnetic fields. They are equal in magnitude but opposite in directions. The induction motor responds to each of the magnetic fields separately. The net torque in the motor is equal to the sum of the torque due to each of the two magnetic fields.
The equation for an alternating magnetic field is given as
b(α) = β max sin w t cos α -----------------------(1)
Where βmax is the maximum value of the sinusoidally distributed air gap flux density produced by a properly distributed stator winding carrying an alternating current of the frequency ω, and α is the space displacement angle measured from the axis of the stator winding.
SinA cosB = ½ sin(A-B) + ½ sin(A+B)
So, the equation (1) becomes
b(α) =1/2 β max sin (w t- α) + ½ β max sin (w t+ α) ------------(2)
The first term of the right-hand side of the equation (2) represents the revolving field moving in the positive α direction. It is known as a Forward Rotating field. Similarly, the second term shows the revolving field moving in the negative α direction and is known as the Backward Rotating field.
The direction in which the single -phase motor is started initially is known as the positive direction. Both the revolving field rotates at the synchronous speed. ωs = 2πf in the opposite direction. Thus, the pulsating magnetic field is resolved into two rotating magnetic fields. Both are equal in magnitude and opposite in direction but at the same frequency.
At the standstill condition, the induced voltages are equal and opposite as a result; the two torques are also equal and opposite. Thus, the net torque is zero and, therefore, a single- phase induction motor has no starting torque.
Application
These are used in low power applications and widely used in domestic applications as well as industrial. And some of those are Pumps, Compressors, Small fans, Mixers, Toys, High speed vacuum cleaners, Electric shavers, Drilling machines
Torque-Speed Characteristics:
There is no direct relation in the speed and torque. At, full load the motor runs at a speed N. When mechanical load increases motor speed decreases till the motor torque again becomes equal to the load torque. As long as two torques are equal the motor runs at constant speed. When the supply frequency increases the speed increases and reduces the maximum torque of motor. So,
Iii) F increases, N increases, Tmax decreases.
Iv) V increases, Tmax increases.
If the above two features are combined, we see that speed increases and torque kept same. If frequency is increased up to certain level and keeping voltage constant the motor speed increases and torque decreases. But when supply frequency is kept same and voltage is increased, then the motor characteristics in this case are stretched and the value of Tmax increases.
Key takeaway
At the standstill condition, the induced voltages are equal and opposite as a result; the two torques are also equal and opposite. Thus, the net torque is zero and, therefore, a single- phase induction motor has no starting torque.
In Separately excited DC motor field windings are used to excite the field flux. Armature current is supplied to the rotor through brush and commutator. When the motor is excited by a field current if and armature current ia flows, the motor develops a back emf and a torque to balance the load torque at a particular speed. The current if is independent of ia. The armature current has no effect on te field current. The current if is less than ia.
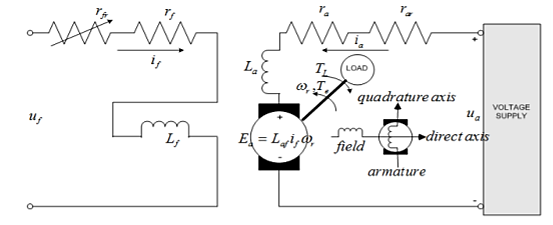
Fig 10 Separately Excited DC Motor
The speed can be controlled by varying voltage in the constant torque region. In the constant power region, field flux should be reduced to achieve speed above the rated speed.
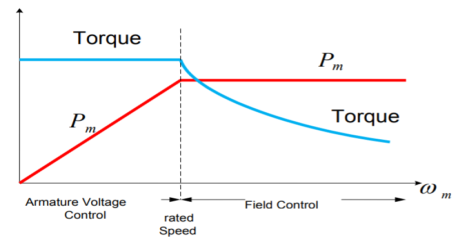
Fig 11: Armature voltage and field current control
An alternator consists of two main parts. The stator is the stationary part of the machine. It carries the armature winding in which the voltage is generated. The rotor is the rotating part of the machine which produces the main field flux. According to the shape of the field, synchronous machines may be classified as cylindrical-rotor (non-salient pole) machines (Figure 1) and salient-pole machines (Figure 2).
Stator construction: The various parts of the stator include the frame stator core stator windings and cooling arrangement.
The frame may be of cost iron for small size machines and a welded Steel tree for large size machines.
To reduce hysteresis, and eddy koi phone current losses, the stator core is assembled with high-grade silicon content steel laminations.
The winding is star connected and is put in the glass cut on the inner periphery of the stator.
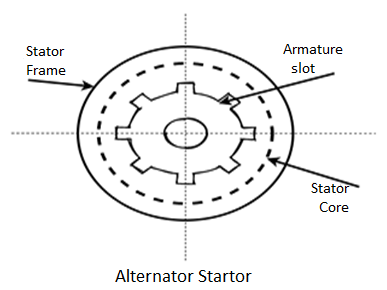
Fig 12 Construction
Rotor construction:
a) Salient pole rotor:
A salient pole rotor consists of poles projecting out from the source of the rotor core.
Salient pole rotors are normally used for routers with four or more poles.
Damper bars are usually inserted in the pole faces to damp out the rotor oscillations during a sudden change in load conditions.
A salient pole synchronous machine has a non-uniform air gap. The air is minimum under the pole centers, and it is maximum in between the poles.
The pull faces are so shaped that the radial autograph length increases from the pole center to the pool ties so that the flux distribution in the air gap is sinusoidal.
The individual field pole windings are connected in series to give an alternative North, and South polarities.
The ends of the field windings are connected to a DC source through the brushes on the slip rings
Salient pole generators have a large number of poles and operate at low speed. A salient pole generator has a comparatively large diameter and a short axial length. The larger diameters accommodate a large number of poles.
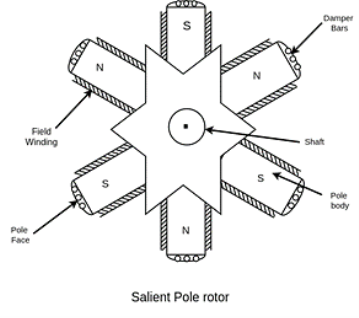
Fig 13 Salient Pole Rotor
b) Cylindrical rotor: -A cylindrical rotor machine is called a non-salient pole rotor machine. It has its rotor so constructed that it forms a smooth cylinder.
Cylindrical rotors are made from solid forgings of high-grade nickel-Chrome-molybdenum steel.
In about two-thirds of the rotor periphery, slots are cut at regular intervals and parallel to the shaft. Field windings are accommodated in these slots. The winding is of distributed type.
The unslotted portion of the rotor from two or four poles.
A cylindrical rotor machine has a comparatively small diameter and long axial length. Such construction limits the centrifugal forces. Thus, cylindrical rotors are particularly useful in high-speed machines.
The cylindrical rotor types alternator has two or four poles on the rotor. Such a construction provides greater mechanical strength and permits more accurate dynamic balancing.
The smooth rotor of the machine makes fewer wind losses, and the operation is less noisy because of the uniform air gap.
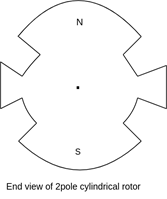
Fig 14 End View of cylindrical rotor
AC generators are usually called an alternator. They are also called synchronous generators. Rotating machines that rotate at a speed fixed by the supply frequency and the number of poles are called synchronous machines.
Most alternators have the rotating field and the stationary armature. The rotating field type alternator has several advantages over the rotating are major type alternators.
- A stationary armature is more easily insulated for the high voltage for which the alternator designs. The generated voltage may be as high as 33kv.
- The armature windings can be braced better mechanically against high electromagnetic forces due to large short-circuit currents when the armature windings are in the stator.
- The armature windings coma being stationary, are not subject to vibration, and centrifugal forces.
- The output current can be taken directly from fixed terminates on the stationary armature without using slip Transcona brushes etc.
- The rotating field is supplied with direct current usually the field voltage is between 100 to 500 balls. Only two rings are required to provide direct current 3 slip rings that would be required for a rotating armature. The insulation of the to relatively low voltage slip rings from the shaft can be provided easily.
- The bulk and weight of the armature windings are substantially greater than the windings of the field poles. The size of the machine is therefore reduced.
- The rotating field is comparatively light and can be constructed for high-speed rotation.
- The stationary armature may be cooled more easily because I am a teacher who can be made large to provide a number of cooling ducts.
Key takeaway
- A salient pole rotor consists of poles projecting out from the source of the rotor core.
- Salient pole rotors are normally used for routers with four or more poles.
- A cylindrical rotor machine is called a non-salient pole rotor machine. It has its rotor so constructed that it forms a smooth cylinder.
- Cylindrical rotors are made from solid forgings of high-grade nickel-Chrome-molybdenum steel.
Rotating-field type and Rotating-armature type
According to the arrangement of the field and armature windings, synchronous machines may be classified as rotating-armature type or rotating-field type.
1. Rotating-Armature Type:
The armature winding is on the rotor and the field system is on the stator. The generated current is brought out to the load via three (or four) slip-rings. Insulation problems, and the difficulty involved in transmitting large currents via the brushes, limit the maximum power output and the generated electromagnetic field (emf). This type is only used in small units, and its main application is as the main exciter in large alternators with brushless excitation systems.
2. Rotating-Field Type:
The armature winding is on the stator and the field system is on the rotor. Field current is supplied from the exciter via two slip-rings, while the armature current is directly supplied to the load. This type is employed universally since very high power can be delivered. Unless otherwise stated, the subsequent discussion refers specifically to rotating-field type synchronous machines.
Excitation systems for synchronous machines:
Excitation means the production of flux by passing current in the field winding direct current is required to excite the field winding on the rotor of the synchronous machines.
For small machines, DC is supplied to the rotor field by a DC generator called exciter. For medium-sized machines, AC excited I used in place of DC excited. The output of an AC exciter is rectified, and supplied through brushes, and slip ring to the rotor windings of the main synchronous machines. For large synchronous generators at present uses brushless excitation systems.
Speed, and frequency:
The frequency of the generated voltage depends upon the number of field poles, and on the speed at which the field poles are rotated.
One complete cycle of voltage is generated in an armature coil when a pair of field poles (one north, and one south pole) passes over the coil.
Let P=total number of field poles
p=pair of field poles
N=speed of the field poles in r.p.m
n=speed of the field poles in r.p.s
F=frequency of the generated voltage in Hz.
& 
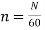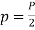
In one revolution of the rotor coma, and the armature coil is cut by 
north poles, and 
south poles.
Since one cycle is generated in an armature coil when a pair of field poles passes over Qualcomm are the number of cycles generated in one revolution of the rotor will be equal to the number of pairs of the pole.
Number of cycles per revolution=p
Also the common number of revolutions per second = n
Frequency =number of cycles per second
=
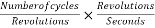
F=p×n
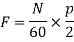
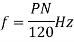
The speed given by the equation is called synchronous speed.
Three phases Synchronous generator (cylindrical rotor type):
Principle of operation: The rotor of the alternator is run at its proper speed by its prime mover. A prime mover is a machine that supplies the mechanical energy input to the alternator. Hydraulic turbines commerce steam and gas turbines are used as prime movers. As the poles of the rotor move under the armature conductor on the status of the file, and flux cut the armature conductors. Therefore voltage is generates in these conductors. This voltage of alternating nature of our sins poles of alternative polarity successively passes by a given stator conductor.
EMF equation and Winding Factor
Let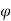 
=useful flux per pole in weber
P=total number of poles.
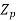=total number of conductors or equal sides in series per phase.
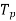=total number of coils or turns per phase.
n=speed of rotation of rotator is revaluation per second.
F=frequency of generated voltage.
Since the flux per Pole is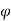 
, each stator conductor cuts a flux 
.
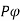The average value of generated voltage per conductor
=(
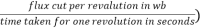
Since n revolutions are made in one second, one revolution will be made in 1/n second. Therefore, the time for one revolution of the armature is 1/n second. The average voltage generated per conductor is
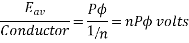
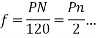
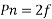
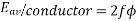
Since there are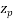 
conductors in series per phase, the average voltage generated per phase are given by
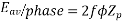
Since.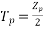
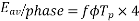
For the voltage wave, the form factor is given by
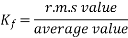
For sinusoidal voltage KF=1.11
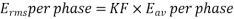
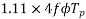
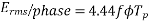
Above equation has been derived with the following assumptions
a) Coils have got a full pitch
b) All the conductors are concentrated in one stator slot.
Winding Factors
Winding Factor: The combined effect of coil span factor and distribution factor is known as winding factor. In fact, winding factor is the product of coil span factor and distribution factor.
Rating of generator
The voltage per phase, current per phase and number of phases defines the rating of generator. It is expressed in MVA or kVA. It can also be defined as the operating voltage between two of its three terminals. For delta connection it equals the phase winding voltage. For star connection it is equal to √3 times the phase-winding voltage.
Generator on no-load and on balanced load.
The factors on which the behavior of synchronous generator depends are on the power factor of load and on the connection. The type of connection means whether it is operating in parallel or alone. Practically, synchronous generators always operate as part of large power systems. Let us consider that the synchronous generator is working alone. According to our assumptions the generator operates at constant speed.
Fig 15 Generator operating alone
The reactive power from generator increases with increase in load. The field current, flux and the field resistor are all constant. Therefore, the speed is also constant keeping the magnitude of internal generated voltage as constant. Assuming the same power factor of the load, change in load will change the magnitude of the armature current IA. However, the angle will be the same (for a constant PF). Thus, the armature reaction voltage jXSIA will be larger for the increased load. Since the magnitude of the internal generated voltage is constant
EA=Vɸ+jXsIA
The basic demand is to generate a constant terminal voltage by generator. By controlling the internal voltage, the terminal voltage is controlled.
EA = K.
This may be done by changing flux in the machine while varying the value of the field resistance RF, which is summarized:
1. Decreasing the field resistance increases the field current in the generator.
2. An increase in the field current increases the flux in the machine.
3. An increased flux leads to the increase in the internal generated voltage.
4. An increase in the internal generated voltage increases the terminal voltage of the generator.
Key takeaway
- For lagging (inductive) loads, the phase (and terminal) voltage decrease.
- For unity power factor (purely resistive) loads, the phase (and terminal) voltage decrease.
- For leading (capacitive) loads, the phase (and terminal) voltage rise.
Armature windings
The winding through which a current is passed to produce the main flux is called the field winding.
The winding in which voltage is induced is called the armature winding some basic terms related to the armature winding are defined as eternal consists of two conductors connected to one end by an end connector. A coil is formed by connecting several turns in series.
A winding is formed by connecting several coils in series.
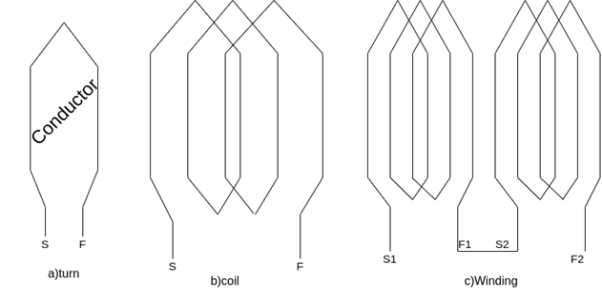
Fig Winding formed by several coils in series
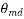=Mechanical degrees or angular measure in space
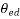= Electrical degree of angular measure in cycles
For p pole machine, the electrical degree is defined as
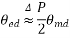
The angular distance between the centers of two adjacent pole on a machine is known as pole pitch or pole span.
One pole pitch=180° elect degree =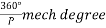
Regardless of the number of poles in the machine, a pole pitch is always 180° electrical degrees.
The two sides of a coil are placed in two slots on the stator surface. The distance between the two sides of a coil is called the coil pitch. If the coil pitch is one pole pitch coma it is called the full pitch coil. If the coil pitch is less than one pole pitch of the coil is called the short pitch coil for fractional pitch coil.
Coil span factor or pitch factor-
The distance between the two sides of a coil is called the coil span or coil pitch.
The angular distance between the central line of one pole to the central line of the next Pole is called pole pitch. A pole pitch is always 180 electrical degrees regardless of the number of poles on the machine.
A coil having a span equal to 180° electrical is called a full pitch coil.
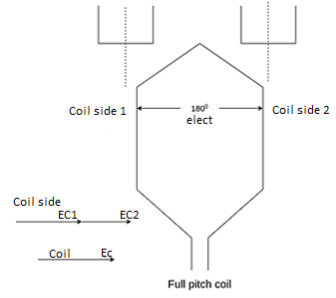
Fig 16 Full Pitch Coil
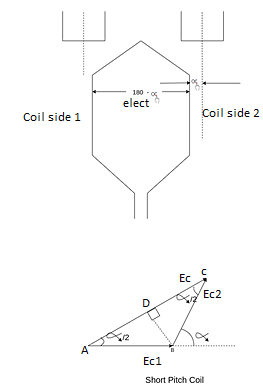
Fig 17 Short Pitch Coil
A coil having a span less than 180° electrical is called a short pitch coil, for fractional pitch coil. It is also called a chorded coil. A stator winding using fractional pitch coils is called a chorded winding. If the span of the coil is reduced by an angle 
electrical degrees, the coil span will be (
) Electrical degrees.
The coil span factor or pitch factor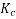 
is defined as the ratio of the voltage generated in the short pitch coil to the voltage generated in the full pitch coil. The coil span factor is also called the chording factor.
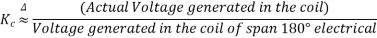
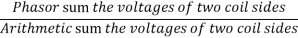
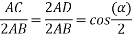
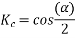
For full pitch coil,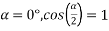 
, and
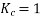For short pitch coil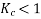 
Advantages of short pitching or chording
1) Shortens the end of the winding, and therefore there is shaving in the conductor material.
2) Reduces the effects of distorting harmonics, and thus the waveform of The generated voltage is improved and making it approach A sine wave.
Distribution factor or breadth factor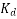 
In a concentrated winding, the coil side of a given face is concentrated in a single slot under a given Pole. The individual coil voltage is induced and is in phase with each other. These voltages may be added arithmetically.
In actual practice, in each phase comic walls are not concentrated in a single slot but are distributed in a number of slots in space to form a polar group under each pole.
The voltages induced in a coil side constituting a polar group are not in the face but differ by an angle equal to the angular displacement of the slots.
The distribution factor or bread factor is defined as the ratio of the actual voltage obtained to the possible voltage if all the coils of a polar group were concentrated in a single slot.
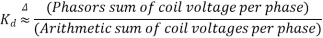
Let m=slots per pole per phase
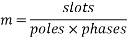
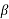= Angular displacement between adjacent slots in electrical degrees
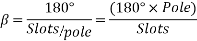
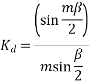
It is to be noted that the distribution factor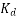 
for a given number of phases is dependent only on the number of distributed slots under a given pole. It is independent of the type of winding, lap or wave, or the number of turns per coil, etc.
As the number of slots per pole increases the distribution factor decreases.
Actual voltage generated
Taking the coil span factor, and distribution factor into account the actual generated voltage per phase is given by
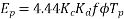
Is called the complete EMF equation of an alternator
The quantity (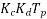
is sometimes called effective turns per phase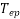 
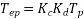
It is smaller than the actual number of turns per face due to fractional pitch coils, and due to the distribution of winding over several slots under each pole.
The coil span factor and distribution of a winding are sometimes combined into a single winding factor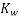 
which is the product of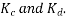 
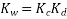
For Star connected alternator the line voltage is √3 times the phase voltage.
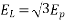
The angle between the terminal voltage v and the internal voltage is the machine angle or rotor angle
Numerical
Example 1. A 3-phase, 50Hz, 8 pole alternator has a star connected winding with 120 slots, and 8 conductors per slot. The flux per Pole is 0.05 WB. Sinusoidally distributed. Determine the phase and line voltages.
The full pitch coil
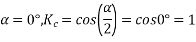
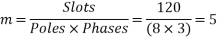
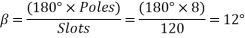
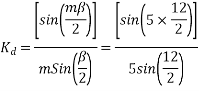
=0.9567
Total number of conductors=conductor per slot × number of slots
Z=8×120=960
Conductors per phase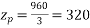 
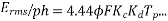
Generated voltage per phase
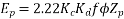
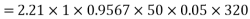
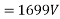
Generated voltage line
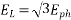
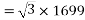
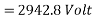
Example 2. A 3 phase 6 pole star connected alternator revolves at 1000 r.p.m. The stator has 90 slots and 8 conductors per slot. The flux per Pole is 0.05 wb (Sinusoidally distributed). Calculate the voltage generated by the machine if the winding factor is 0.96.
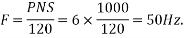
Total number of stator conductors=conductors per slots × number of slots
=8×90=720
Stator conductors per phase
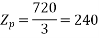
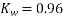
Generated voltage per phase
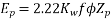
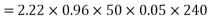
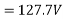
Generated line voltage=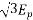
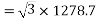
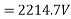
Example 3. A 3 phase, 16 Pole synchronous generator has a resultant air-gap flux of 0.06 wb per pole. The flux is distributed sinusoidally over the pole. The stator has two slots per pole per phase, and 4 conductors per slot are accommodated in two layers. The coil span is 150° electrical. Calculate the phase, and line induced voltage when the machine runs at 375 r.p.m.
m=Slots per pole per phase=2
Total slots=2×16×3=96
Total number of conductors=slots × conductors per slot
=96×4
=384
Number of conductors per phase
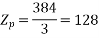
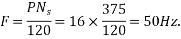
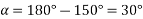
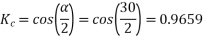
The angular displacement between adjacent slots
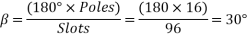
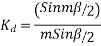
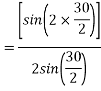
=0.9659
Since the flux is sinusoidally distributed
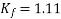
The generated voltage per phase is given by
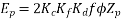
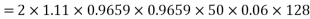
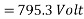
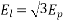
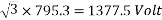
Example 4. A 3 phase, 50 hertz, 2 pole star connected turbo alternator has 54 slots with 4 conductors per slot the pitch of the coils is two slots less than the pole pitch. If the machine gives 3300V between lines on the open circuit with sinusoidal flux distribution, determine the useful flux per pole.
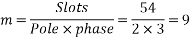
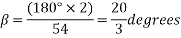
Coil pitch=25 slot angles
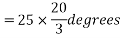
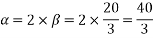
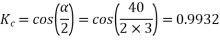
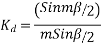
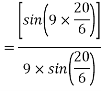
=0.95547
Total number of conductors per phase=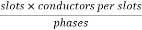
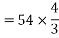
=72
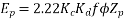
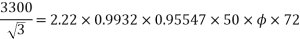
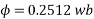
Example 5. A 4 pole, 3 phase, 50-hertz star connected alternator has 60 slots with two conductors per slot and having armature winding of two-layer type quasar short-pitched in such a way that if one coil sides lie in slot number one of the other lies in slot number 13. Determine the useful flux purple required to generate line voltage of 6000 volt.
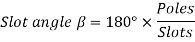
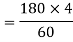
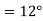
Coil Span=12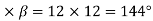
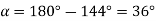
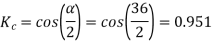
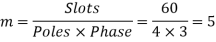
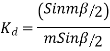
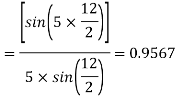
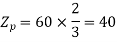
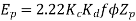
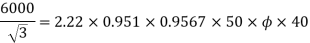
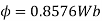
Armature leakage reactance:
In an AC machine, any flux set up by the load current which does not contribute to the useful flux of the machine is a leakage flux.
The effect of this leakage flux is to set up a self-induced emf in the armature winding the leakage flux is may be classified as
- Slot leakage
- Tooth head leakage
- Coil end for overhang leakage.
The voltage induced in the armature windings by the air gap flux is called air gap voltages.
The leakage flux also induces a voltage in the armature winding these are taken into account by introduction of leakage reactance drops. Most of the reluctances of the magnetic circuits for armature leakage fluxes are due to air paths. The fluxes are, therefore nearly proportional to the armature current producing them and are in phase with these currents. The voltage induced in the armature windings can be considered with the leakage reactance drops, and lead the current producing them by 90.
Armature reaction in synchronous machines:
When current flows through the armature winding of an alternator the resultant MMF produces flux. The armature flux reacts with main Pole flux causing the resultant flux to become either less than or more than the original main field flux. (The effect of armature (stator) flux on the flux produced by the rotor field poles is called armature reaction).
For simplicity, we considered a 3 phase 2 pole alternator having a single layer winding but this treatment is valid for any number of poles. Also the winding of each phase is assumed to be concentrated but the effect of armature reaction will be the same as if a distributed winding were used.
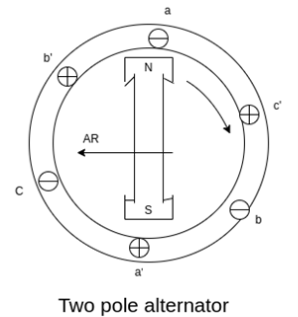
Fig 18 Two pole alternator
The power factor will be defined as the cosine of the angle between the armature phase current, and the induced EMF in the armature conductor in that phase.
a) Armature reaction at unity power factor:
Suppose that the alternator is supplying current at unity power factor the phase currents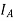 
, 
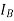, and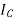 
will be in phase with their respective generated voltage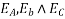 
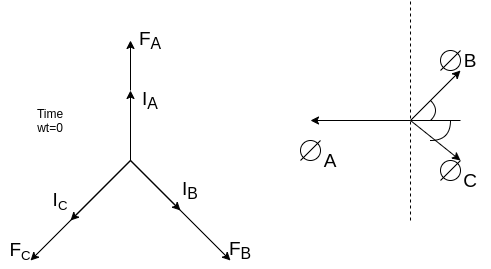
Fig 19 Phasor for UPF
The projections of phasor on the vertical Axis gives its instantaneous value. At t=0, the instantaneous values of the currents and fluxes are given by.
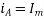
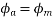
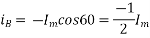
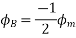
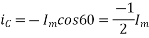
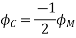
Where the subscript m denotes the maximum value of current, and flux.
Since the fluxes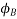 
, and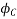 
are negative. They are acting opposite to the direction shown above. They are shown by OB, and OC. The resultant of the fluxes can be found by resolving the fluxes horizontally and vertically
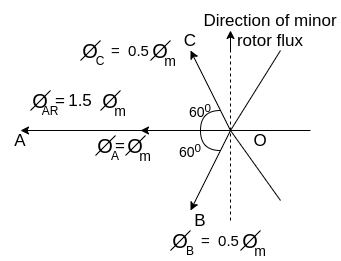
Fig 20 Direction of minor rotor flux
Resolving along the horizontal direction we get
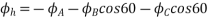
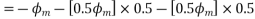
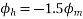
Resolving along the vertical direction we get
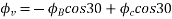
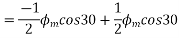
=0
The resultant armature reaction flux is given by
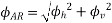
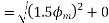
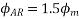
The direction of this resultant flux is along OA, and the resultant armature reaction flux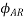 
is constant in magnitude equal to 1.5
.
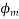Also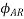 
lags behind 90 with the main field flux. This is called the cross-magnetizing flux.
b. Armature reaction: -Lagging power factor
Suppose that the alternator is loaded with an inductive load of zero power factor lagging. The phase current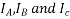 
will be lacking with their respective phase voltage 
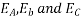by 90°.
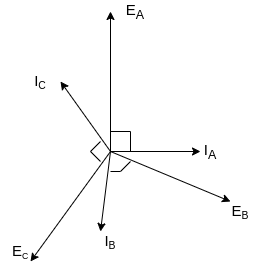
Fig 21 Phasor for Lagging power factor
At time t=0 the instantaneous values of currents and fluxes are given by
, 
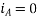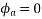
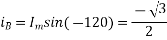
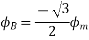
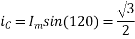
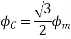
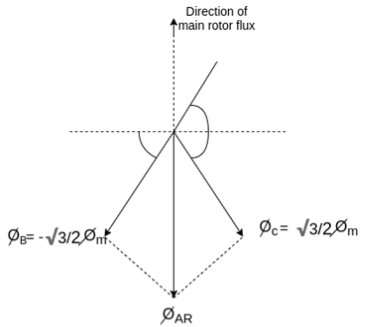
Fig 22 Direction of main rotor flux
The resultant flux is
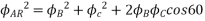
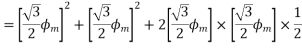
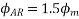
It is seen that the direction of the armature reaction flux is opposite to the main field flux. Therefore, it will oppose, and weaken the main field flux. It is said to be demagnetizing.
c. Armature reaction: Leading power factor
Suppose that the alternator is loaded with a load of zero power factor leading. The phase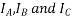 
will be leading their respective phase voltages 
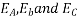by 90°
At time t=0 the instantaneous values of currents and fluxes are given by
, 
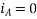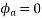
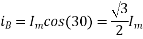
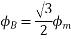
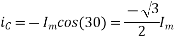
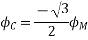
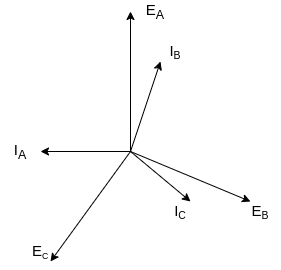
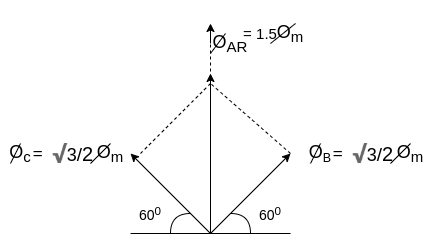
Fig 23 Phasor for Leading power factor
The resultant flux is given by
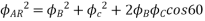
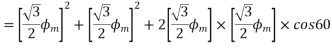
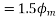
It is seen that the direction of the armature reaction flux is in the direction of the main field flux. Does it will aid it. In other words, it is a magnetizing flux.
Synchronous Impedance: -
The actual generated voltage consists of the summation of two-component voltages. One of these component voltages is the voltage that would be generated if there were no armature reaction. It is the voltage that would be generated because of only the field excitation. This component of the generated voltage is called the excitation voltage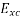 
.
The other component of the generated voltage is called the armature reaction voltage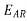
.
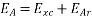
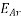is the equivalent to a voltage of inductive reactance, and
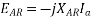
In addition to the effects of armature reaction, the stator winding also has a self-inductance and a resistance.
Let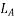 
= self-inductance of the stator winding
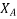= self inductive reactance of stator winding
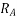=armature resistance
The terminal voltage V is given by
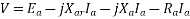
Where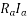 
=armature resistance drop
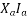=armature leakage reactance drop
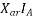=armature reaction voltage
Synchronous reactance can be represented as
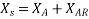
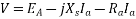
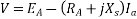
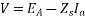
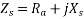
The impedance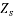 
is called the synchronous impedance.
Key takeaway
In an AC machine, any flux set up by the load current which does not contribute to the useful flux of the machine is a leakage flux.
The effect of this leakage flux is to set up a self-induced emf in the armature winding the leakage flux is may be classified as
- Slot leakage
- Tooth head leakage
- Coil end for overhang leakage.
Equivalent circuit, and phasor diagram of a synchronous generator
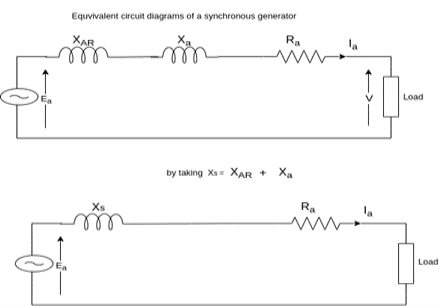
Fig 24 Equivalent Circuit Diagram of Synchronous Generator
a) Unity power factor
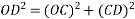
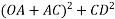
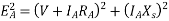
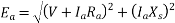
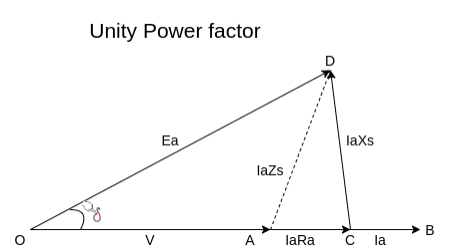
Fig 25 Phasor for UPF
b) Lagging power factor
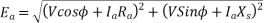
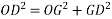
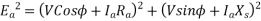
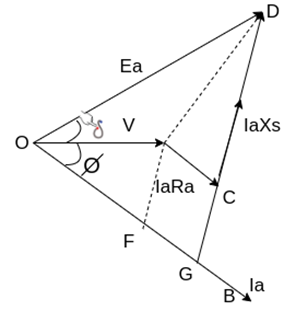
Fig 26 Phasor for Lagging PF
c) Leading power factor
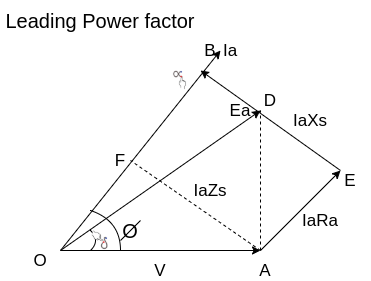
Fig 27 Phasor for leading power factor
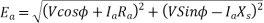
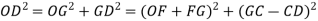
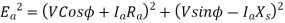
Problem
A 3 phase 16 pole alternator has a star connected winding with 144 slots, and 10 conductors per slot. The flux per pole=0.03 Wb sinusoidally distributed, and speed is 375 rpm.
Find
1) Frequency
2) Phase voltage
3) Line voltage
Solution
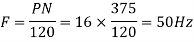
Total conductors= 144×10=1440
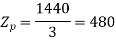
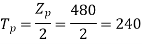
For 
as coil pitch is not mentioned take full pitched coil.
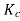=1
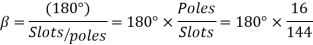
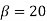
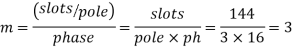
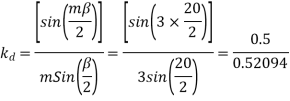
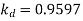
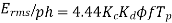
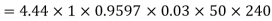
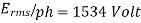
For star connection,
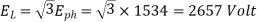
Problem
A 3 phase 4 pole alternator has 60 slots, two conductors per slot. The pitch of the coils is 3 slots less than full pitch. Find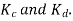 
Pole pitch=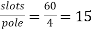
Now 15 slots=180
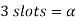
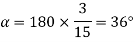
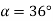
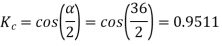
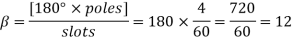
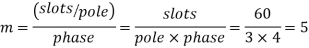
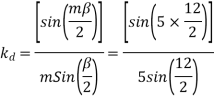
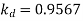
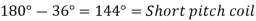
Sr.No. | Salient pole type synchronous machine | Non-salient pole type synchronous machine |
1 | Diagram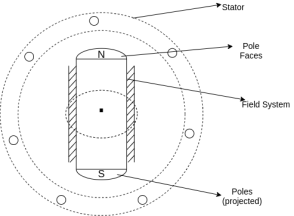 
| Diagram  |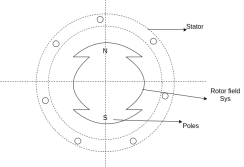
2 | Projected out poles | Merged in polls |
3 | Rotor surface is projected | Smooth rotor surface |
4 | The diameter of the machine is large | The small diameter of the machine |
5 | The axial length of the machine is small | The axial length of the machine is large |
6 | Speed is slow | Speed is high |
7 | Air gap is non uniform | Air gap is uniform |
8 | Damper bars/winding is used | Damper bar/winding not used |
9 | The air gap between stator and rotor is non-uniform | The air is uniform between stator and rotor |
10 | Centrifugal stress is more | Centrifugal stress is less |
11 | Aerodynamic resistance is more | Aerodynamic resistance is less |
Key takeaway
Average emf induced/conductor is
= 
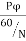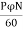
The induced /phase is given by
Eph = 4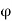
f Tph x 1.11=4.44
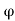f Tph
References:
- D. P. Kothari and I. J. Nagrath, “Basic Electrical Engineering”, Tata McGraw Hill, 2010.
- D. C. Kulshreshtha, “Basic Electrical Engineering”, McGraw Hill, 2009.
- L. S. Bobrow, “Fundamentals of Electrical Engineering”, Oxford University Press, 2011.
- E. Hughes, “Electrical and Electronics Technology”, Pearson, 2010.
- V. D. Toro, “Electrical Engineering Fundamentals”, Prentice Hall India, 1989.
