Unit - 3
Vector Space
Definition-
Let ‘F’ be any given field, then a given set V is said to be a vector space if-
1. There is a defined composition in ‘V’. This composition called addition of vectors which is denoted by ‘+’
2. There is a defined an external composition in ‘V’ over ‘F’. That will be denoted by scalar multiplication.
3. The two compositions satisfy the following conditions-
(a) 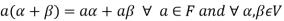
(b) 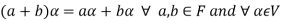
(c) 
(d) If 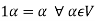 then 1 is the unity element of the field F.
then 1 is the unity element of the field F.
If V is a vector space over the field F, then we will denote vector space as V(F).
Note that each member of V(F) will be referred as a vector and each member of F as a scalar
Note- Here we have denoted the addition of the vectors by the symbol ‘+’. This symbol also be used for the addition of scalars.
If  then
then 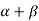 represents addition in vectors(V).
represents addition in vectors(V).
If  then a+b represents the addition of the scalars or addition in the field F.
then a+b represents the addition of the scalars or addition in the field F.
Note- For V to be an abelian group with respect to addition vectors, the following conditions must be followed-
1. 
2. 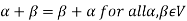
3.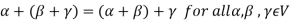
4. There exists an element 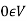 which is also called the zero vector. Such that-
which is also called the zero vector. Such that-
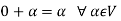
It is the additive identity in V.
5. There exists a 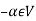 to every vector
to every vector 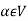 such that
such that
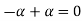
This is the additive inverse of V
Note- All the properties of an abelian group will hold in V if (V,+) is an abelian group.
These properties are-
1. 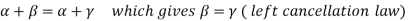
2. 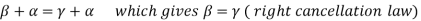
3. 
4. 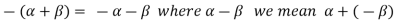
5. The additive identity 0 will be unique.
6. The additive inverse will be unique.
7. 
Note- The Greek letters 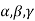 are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
Note- Suppose C is the field of complex numbers and R is the field of real numbers, then C is a vector space over R, here R is the subfield of C.
Here note that R is not a vector space over C.
Example-: The set of all 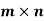 matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
Sol. V is an abelian group with respect to addition of matrices in groups.
The null matrix of m by n is the additive identity of this group.
If  then
then 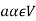 as
as 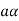 is also the matrix of m by n with elements of real numbers.
is also the matrix of m by n with elements of real numbers.
So that V is closed with respect to scalar multiplication.
We conclude that from matrices-
1. 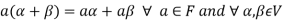
2. 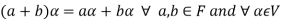
3. 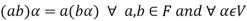
4. 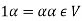 Where 1 is the unity element of F.
Where 1 is the unity element of F.
Therefore we can say that V (F) is a vector space.
Example-2: The vector space of all polynomials over a field F.
Suppose F[x] represents the set of all polynomials in indeterminate x over a field F. The F[x] is vector space over F with respect to addition of two polynomials as addition of vectors and the product of a polynomial by a constant polynomial.
Example-3: The vector space of all real valued continuous (differentiable or integrable) functions defined in some interval [0,1]
Suppose f and g are two functions, and V denotes the set of all real valued continuous functions of x defined in the interval [0,1]
Then V is a vector space over the filed R with vector addition and multiplication as:
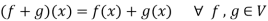
And
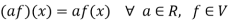
Here we will first prove that V is an abelian group with respect to addition composition as in rings.
V is closed with respect to scalar multiplication since af is also a real valued continuous function
We observe that-
1. If 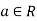 and f,g
and f,g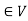 , then
, then
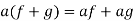
2. If  and
and  , then
, then
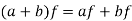
3. If 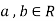 and
and 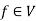 , then
, then
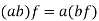
4. If 1 is the unity element of R and  , then
, then
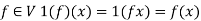
So that V is a vector space over R.
Some important theorems on vector spaces-
Theorem-1: Suppose V(F) is a vector space and 0 be the zero vector of V. Then-
1. 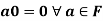
2. 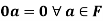
3. 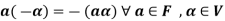
4. 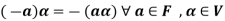
5. 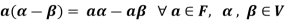
6. 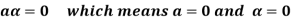
Proof-
1. We have

We can write 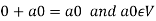
So that,
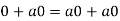
Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-
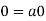
2. We have
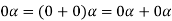
We can write 
So that,
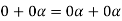
Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-
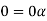
3. We have 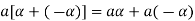
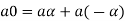
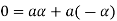
 is the additive inverse of
is the additive inverse of 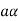

4. We have 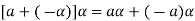


 is the additive inverse of
is the additive inverse of 
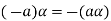
5. We have-
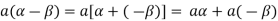
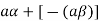
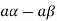
6. Suppose 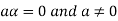 the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.
the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.
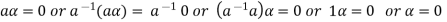
Again let-
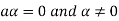 , then to prove
, then to prove 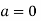 let
let 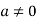 then inverse of ‘a’ exists
then inverse of ‘a’ exists
We get a contradiction that 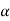 must be a zero vector. Therefore ‘a’ must be equal to zero.
must be a zero vector. Therefore ‘a’ must be equal to zero.
So that

Vector Sub Space
Definition
Suppose V is a vector space over the field F and 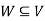 . Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
. Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
Theorem-1-The necessary and sufficient conditions for a non-empty sub-set W of a vector space V(F) to be a subspace of V are-
1. 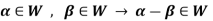
2. 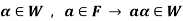
Proof:
Necessary conditions-
W is an abelian group with respect to vector addition If W is a subspace of V.
So that 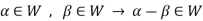
Here W must be closed under a scalar multiplication so that the second condition is also necessary.
Sufficient conditions-
Let W is a non-empty subset of V satisfying the two given conditions.
From first condition-
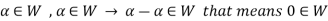
So that we can say that zero vector of V belongs to W. It is a zero vector of W as well.
Now 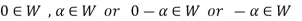
So that the additive inverse of each element of W is also in W.
So that-

Thus W is closed with respect to vector addition.
Theorem-2:
The intersection of any two subspaces  and
and 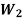 of a vector space V(F) is also a subspace of V(F).
of a vector space V(F) is also a subspace of V(F).
Proof: As we know that  therefore
therefore 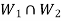 is not empty.
is not empty.
Suppose 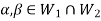 and
and 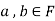
Now, 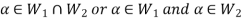
And 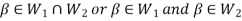
Since  is a subspace, therefore-
is a subspace, therefore-
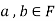 and
and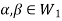 then
then 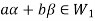
Similarly, 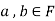
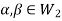 then
then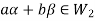
Now 
Thus,
 And
And 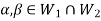
Then 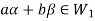
So that  is a subspace of V(F).
is a subspace of V(F).
Example-1: If 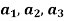 are fixed elements of a field F, then set of W of all ordered triads (
are fixed elements of a field F, then set of W of all ordered triads (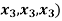 of elements of F,
of elements of F,
Such that-

Is a subspace of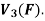
Sol. Suppose 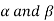 are any two elements of W.
are any two elements of W.
Such that 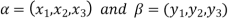
And these are the elements of F, such that-
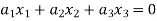 …………………….. (1)
…………………….. (1)
 ……………………. (2)
……………………. (2)
If a and b are two elements of F, we have
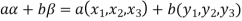
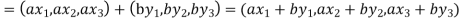
Now
= 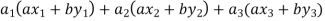
= 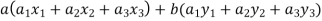
= 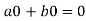
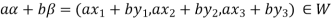
So that W is subspace of 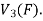
Example-2: Let R be a field of real numbers. Now check whether which one of the following are subspaces of 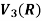
1. { 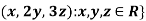
2. { 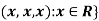
3. { 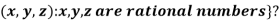
Solution- 1. Suppose W = { 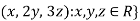
Let  be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-
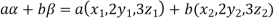
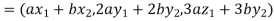
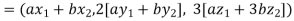
Since 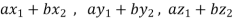 are real numbers.
are real numbers.
So that 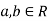 and
and 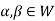 or
or 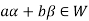
So that W is a subspace of 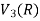
2. Let W = { 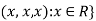
Let 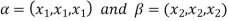 be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-

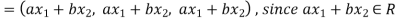
So that W is a subspace of 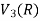
3. Let W ={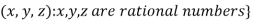
Now 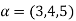 is an element of W. Also
is an element of W. Also  is an element of R.
is an element of R.
But 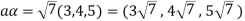 which do not belong to W.
which do not belong to W.
Since 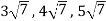 are not rational numbers.
are not rational numbers.
So that W is not closed under scalar multiplication.
W is not a subspace of 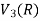
Key takeaways:
- If V is a vector space over the field F, then we will denote vector space as V(F).
- If
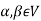 then
then 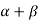 represents addition in vectors(V).
represents addition in vectors(V). - For V to be an abelian group with respect to addition vectors, the following conditions must be followed-
1. 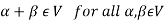
2. 
3.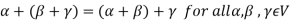
4. All the properties of an abelian group will hold in V if (V,+) is an abelian group.
5. The Greek letters 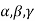 are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
are used to denote elements of vectors and Latin letters a , b , c etc. for scalars that means the elements of field F.
6. Suppose V is a vector space over the field F and  . Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
. Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
In the theory of vector spaces, a set of vectors is said to be linearly dependent if at least one of the vectors in the set can be defined as a linear combination of the others; if no vector in the set can be written in this way, then the vectors are said to be linearly independent. These concepts are central to the definition of dimension.
Linear Dependence and Independence: The set of vectors 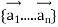 in an vector space V is said to be Linearly dependent if there exist scalars
in an vector space V is said to be Linearly dependent if there exist scalars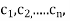 not all zero such that
not all zero such that
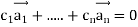
Example 1: Are  linearly independent?
linearly independent?
Independent if 
Has only the trivial solution 
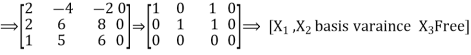
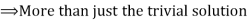

Example 2: Check whether the vectors 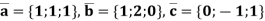 are independent.
are independent.
Solution: Calculate the coefficients in which a linear combination of these vectors vector.
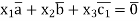
This vector equation can be written as a system of linear equations
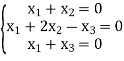
Solve this system using the gauss method
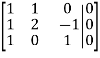
From 2 row we subtract the 1-th row; from 3row we subtract the 1-th row:
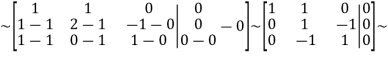
From 1 row we subtract the 2row; for 3 row add 2 row:
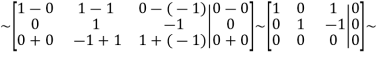
This solution shows that the system has many solutions, i.e exist nonzero combination c such that the linear combination of 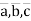 is equal to the zero vector,
is equal to the zero vector,
For Example, 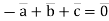
Means vectors 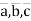 are linearly dependent.
are linearly dependent.
Answer: Vectors 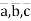 are linearly dependent.
are linearly dependent.
Key takeaways:
- Let V(F) be a vector space. A finite set
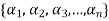 of vector of V is said to be linearly dependent if there exists scalars
of vector of V is said to be linearly dependent if there exists scalars 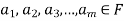 (not all of them as some of them might be zero) such that-
(not all of them as some of them might be zero) such that-

2. The set of non-zero vectors  of V(F) is linearly dependent if some
of V(F) is linearly dependent if some  Is a linear combination of the preceding ones.
Is a linear combination of the preceding ones.
Linear independence-
Let V(F) be a vector space. A finite set 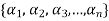 of vector of V is said to be linearly independent if every relation if the form-
of vector of V is said to be linearly independent if every relation if the form-

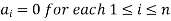
Theorem:
The set of non-zero vectors 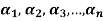 of V(F) is linearly dependent if some
of V(F) is linearly dependent if some 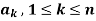
Is a linear combination of the preceding ones.
Proof:
If some 
Is a linear combination of the preceding ones, 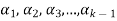 then ∃ scalars
then ∃ scalars 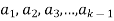 such that-
such that-
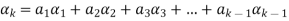 …… (1)
…… (1)
The set {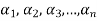 } is linearly dependent because the linear combination (1) the scalar coefficient
} is linearly dependent because the linear combination (1) the scalar coefficient 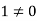
Hence the set { } of which {
} of which { } is a subset must be linearly dependent.
} is a subset must be linearly dependent.
Example-1: If the set S = 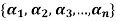 of vector V(F) is linearly independent, then none of the vectors
of vector V(F) is linearly independent, then none of the vectors 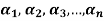 can be zero vector.
can be zero vector.
Sol. Let 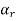 be equal to zero vector where
be equal to zero vector where 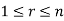
Then 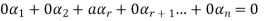
For any  in F.
in F.
Here 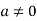 therefore from this relation we can say that S is linearly dependent. This is the contradiction because it is given that S is linearly independent.
therefore from this relation we can say that S is linearly dependent. This is the contradiction because it is given that S is linearly independent.
Hence none of the vectors can be zero.
We can conclude that a set of vectors which contains the zero vector is necessarily linear dependent.
Example-2: Show that S = {(1 , 2 , 4) , (1 , 0 , 0) , (0 , 1 , 0) , (0 , 0 , 1)} is linearly dependent subset of the vector space 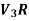 . Where R is the field of real numbers.
. Where R is the field of real numbers.
Sol. Here we have-
1 (1 , 2 , 4) + (-1) (1 , 0 , 0) + (-2) (0 ,1, 0) + (-4) (0, 0, 1)
= (1, 2 , 4) + (-1 , 0 , 0) + (0 ,-2, 0) + (0, 0, -4)
= (0, 0, 0)
That means it is a zero vector.
In this relation the scalar coefficients 1 , -1 , -2, -4 are all not zero.
So that we can conclude that S is linearly dependent.
Example-3: If 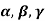 are linearly independent vectors of V(F).where F is the field of complex numbers, then so also are
are linearly independent vectors of V(F).where F is the field of complex numbers, then so also are  .
.
Sol. Suppose a, b, c are scalars such that-
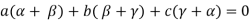
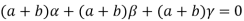 …………….. (1)
…………….. (1)
But 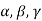 are linearly independent vectors of V(F), so that equations (1) implies that-
are linearly independent vectors of V(F), so that equations (1) implies that-
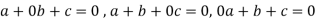
The coefficient matrix A of these equations will be-
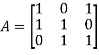
Here we get rank of A = 3, so that a = 0, b = 0, c = 0 is the only solution of the given equations, so that  are also linearly independent.
are also linearly independent.
Definition:
A subset S of a vector space V(F) is said to be a basis of V(F), if-
1. S consists of linearly independent vectors
2. Each vector in V is a linear combination of a finite number of elements of S.
Finite dimensional vector spaces
The vector space V(F) is said to be finite dimensional if there exists a finite subset S of V such that V = L(S).
Dimension theorem for vector spaces-
Statement- If V(F) is a finite dimensional vector spaces, then any two bases of V have the same number of elements.
Proof: Let V(F) is a finite dimensional vector space. Then V possesses a basis.
Let 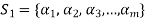 and
and 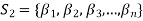 be two bases of V.
be two bases of V.
We shall prove that m = n
Since V = L(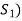 and
and 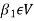 therefore
therefore 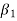 can be expressed as a linear combination of
can be expressed as a linear combination of 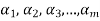
Consequently the set 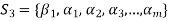 which also generates V(F) is linearly dependent. So that there exists a member
which also generates V(F) is linearly dependent. So that there exists a member 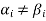 of this set. Such that
of this set. Such that 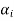 is the linear combination of the preceding vectors
is the linear combination of the preceding vectors 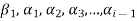
If we omit the vector 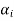 from
from 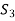 then V is also generated by the remaining set.
then V is also generated by the remaining set.
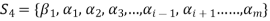
Since V = L( and
and 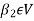 therefore
therefore 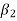 can be expressed as a linear combination of the vectors belonging to
can be expressed as a linear combination of the vectors belonging to 
Consequently the set-
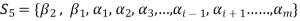
Is linearly dependent.
Therefore there exists a member 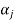 of this set such that
of this set such that 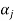 is a linear combination of the preceding vectors. Obviously
is a linear combination of the preceding vectors. Obviously 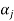 will be different from
will be different from 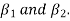
Since {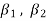 } is a linearly independent set
} is a linearly independent set
If we exclude the vector 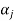 from
from 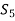 then the remaining set will generate V(F).
then the remaining set will generate V(F).
We may continue to proceed in this manner. Here each step consists in the exclusion of an 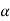 and the inclusion of
and the inclusion of 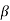 in the set
in the set 
Obviously the set 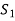 of all
of all  can not be exhausted before the set
can not be exhausted before the set 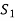 and
and 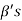
Otherwise V(F) will be a linear span of a proper subset of 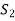 thus
thus 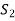 become linearly dependent. Therefore we must have-
become linearly dependent. Therefore we must have-

Now interchanging the roles of  we shall get that
we shall get that 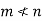
Hence,
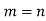
Extension theorem-
Every linearly independent subset of a finitely generated vector space V(F) forms of a part of a basis of V.
Proof: Suppose 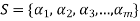 be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say
be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say 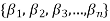
Let us consider a set-
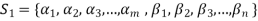 …………. (1)
…………. (1)
Obviously L(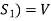 , since there
, since there 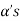 can be expressed as linear combination of
can be expressed as linear combination of 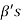 therefore the set
therefore the set 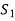 is linearly dependent.
is linearly dependent.
So that there is some vector of 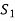 which is linear combination of its preceding vectors. This vector can not be any of the
which is linear combination of its preceding vectors. This vector can not be any of the 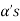 since the
since the  are linearly independent.
are linearly independent.
Therefore this vector must be some  say
say 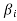
Now omit the vector 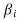 from (1) and consider the set-
from (1) and consider the set-

Obviously L(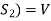 . If
. If 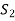 is linearly independent, then
is linearly independent, then 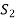 will be a basis of V and it is the required extended set which is a basis of V.
will be a basis of V and it is the required extended set which is a basis of V.
If 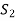 is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing
is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing 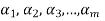 and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of
and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of 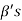 will be adjoined to S so as to form a basis of V.
will be adjoined to S so as to form a basis of V.
Example-1: Show that the vectors (1, 2, 1), (2, 1, 0) and (1, -1, 2) form a basis of 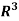
Sol. We know that set {(1,0,0) , (0,1,0) , (0,0,1)} forms a basis of 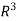
So that dim 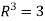 .
.
Now if we show that the set S = {(1, 2, 1), (2, 1, 0) , (1, -1, 2)} is linearly independent, then this set will form a basis of 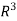
We have,
 (1, 2, 1)+
(1, 2, 1)+ (2, 1, 0)+
(2, 1, 0)+ (1, -1, 2) = (0, 0, 0)
(1, -1, 2) = (0, 0, 0)
(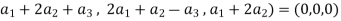
Which gives-
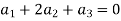

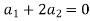
On solving these equations we get,
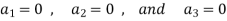
So we can say that the set S is linearly independent.
Therefore it forms a basis of 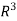
Example 1: Is the set S = {(1,1),(1,-1)} a basis for 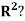
- Does S span
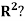
Solve 
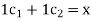
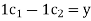
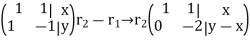
This system is consistent for every x and y, therefore S spans 
2.IS S linearly independent?
Solve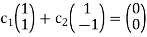
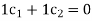
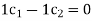
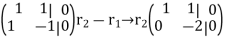
The system has a unique solution  (trivial solution)
(trivial solution)
Therefore, S is linearly independent.
Consequently, S is a basis for 
Example 2: 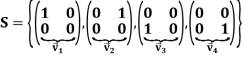
Is a basis for the vector space 
1.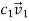 +
+
Is equivalent to:
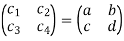
Which is consistent for every a,b,c and d.
Therefore, S spans 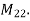
2.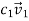 +
+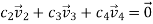 is equivalent to:
is equivalent to:
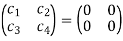
The system has only the trivial solution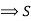 is linearly independent.
is linearly independent.
Consequently, S is a basis for 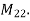
Key takeaways:
- The vector space V(F) is said to be finite dimensional if there exists a finite subset S of V such that V = L(S).
- If V(F) is a finite dimensional vector spaces, then any two bases of V have the same number of elements.
- Every linearly independent subset of a finitely generated vector space V(F) forms of a part of a basis of V.
Definition-
Suppose U(F) and V(F) are two vector spaces, then a mapping  is called a linear transformation of U into V, if:
is called a linear transformation of U into V, if:
1. 
2. 
It is also called homomorphism.
Kernel of a linear transformation-
Let f be a linear transformation of a vector space U(F) into a vector space V(F).
The kernel W of f is defined as-
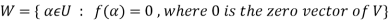
The kernel W of f is a subset of U consisting of those elements of U which are mapped under f onto the zero vector V.
Since f(0) = 0, therefore atleast 0 belong to W. So that W is not empty.
Example: The mapping 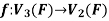 defined by-
defined by-
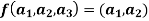
Is a linear transformation 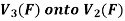 .
.
What is the kernel of this linear transformation.
Sol. Let 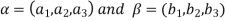 be any two elements of
be any two elements of 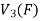
Let a, b be any two elements of F.
We have
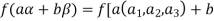 (
(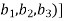
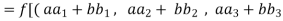
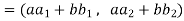
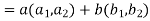 =
= 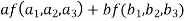
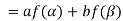
So that f is a linear transformation.
To show that f is onto 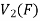 . Let
. Let 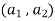 be any elements
be any elements 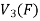 .
.
Then  and we have
and we have 
So that f is onto 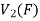
Therefore f is homomorphism of 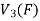 onto
onto  .
.
If W is the kernel of this homomorphism then 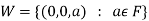
We have
∀
Also if 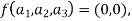 then
then 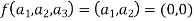
Implies 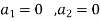
Therefore 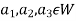
Hence W is the kernel of f.
Theorem: Let L: V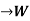 . Then ker L is a subspace of V.
. Then ker L is a subspace of V.
Proof: Notice that if L(v)=0 and L(u)=0, then for any constants c,d, L(cu+dv)=0.
Then by the subspace theorem, the kernel of L is a subspace of V.
This theorem has a nice interpretation in terms of the eigenspace of L. Suppose L has a zero eigenvalue. Then the associated eigenspace consists of all vectors v such that Lv=0v=0; in other words , the 0-eigenspace of L is exactly the kernel of L
Returning to the previous example, let L(x,y) =(x+y,x+2y,y). L is clearly not surjective, Since L sends  to a plane in
to a plane in 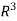 .
.
Notice that if x = L(v) and y = L(v), then for any constants c,d then cx+dy=L(cx+du). Then the subspace theorem strikes again, and we have the following theorem.
Example 1: 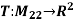 defined by
defined by  is linear. Describe its kernel and range and give the dimension of each.
is linear. Describe its kernel and range and give the dimension of each.
It should be clear that 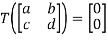 if, and only if, b= -a and d= -c. The kernel of T is therefore all matrices of the form
if, and only if, b= -a and d= -c. The kernel of T is therefore all matrices of the form
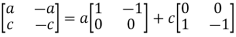
The two matrices 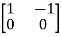 and
and 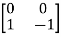 are not scalar multiples of each other, so they must be linearly independent. Therefore, the dimension of ker(T) is two.
are not scalar multiples of each other, so they must be linearly independent. Therefore, the dimension of ker(T) is two.
Now suppose that we have any vector  Clearly
Clearly  . So, the range of T of
. So, the range of T of  Thus the dimension of ran(T)is two.
Thus the dimension of ran(T)is two.
Example 2: 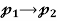 defined by T(ax+b) = 2bx-a is linear. Describe its kernel and range and give the dimension of each.
defined by T(ax+b) = 2bx-a is linear. Describe its kernel and range and give the dimension of each.
T(ax+b) =2bx-a=0 if, and only if, both a and b are zero. Therefore, the kernel of T is only the zero polynomial. By definition, the dimension of the subspace consisting of only the zero vector is zero, so ker(T) has dimension zero.
Suppose that we take a random polynomial cx+d in the codomain. If we consider the polynomial -dx+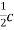 in the domain we see that
in the domain we see that
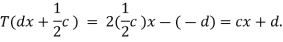
This shows that the range of T is all of  it has dimension two.
it has dimension two.
Key takeaways:
1. Suppose U(F) and V(F) are two vector spaces, then a mapping  is called a linear transformation of U into V, if:
is called a linear transformation of U into V, if:
1. 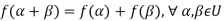
2. 
It is also called homomorphism.
2. Let f be a linear transformation of a vector space U(F) into a vector space V(F).
The kernel W of f is defined as-
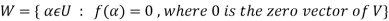
Rank-nullity theorem:
Statement: Let V,W be vector spaces, where V is finite dimensional. Let T: V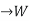 be a linear transformation. Then
be a linear transformation. Then
Rank(T)+Nullity(T) = dim
Where
Rank(T) = dim(Image(T)) and Nullity(T) = dim(Ker(T))
Proof: Let V, W be vector spaces over some field F and T defined as in the statement of the theorem with dim V = n
As Ker (T) 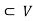 is a subspace, there exists a basis for it. Suppose
is a subspace, there exists a basis for it. Suppose
Dim Ker (T) = k and let
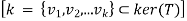

Be such a basis.
We may now, by the Steinitz exchange lemma, extend 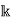 with n-k linearly independent vectors
with n-k linearly independent vectors  to form a full basis of V.
to form a full basis of V.
Let
S = 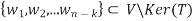

Such that
B=  =
= 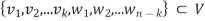
Is a basis for V.
From this, we know that
Im T = SpanT(B) = Span 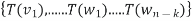 = Span(T)
= Span(T)
We now claim that T(S) is a basis for ImT. By definition, T(S) is generating; it remains to be shown that it is also linearly independent to conclude that it is a basis.
Suppose T(s) is not linearly independent, and let
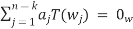
For some 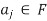 .
.
Thus, owing to the linearity of T, it follows that
T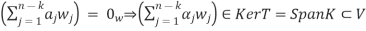

This is a contradiction to B being a basis, unless all  are equal to zero. This shows that T(S) is linearly independent, and more specifically that it is a basis for ImT .To summarise, we have K, a basis for Ker T, and T(S), a basis for ImT.
are equal to zero. This shows that T(S) is linearly independent, and more specifically that it is a basis for ImT .To summarise, we have K, a basis for Ker T, and T(S), a basis for ImT.
Finally, we may state that
Rank(T)+Nullity(T)=dim ImT+ dimKer T=
This concludes our proof.
Inverse of a Matrix:
To understand this concept better let us take a look at the following example.
The Inverse of Linear Transformation:
Definition: A function T from X to Y is called invertible if the equation T(x)=y has a unique solution x in X for each y in Y.
Denote the inverse of T as 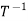 from Y to X, and write
from Y to X, and write
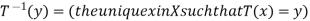
Note
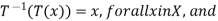

If a function T is invertible, then so is 
Example 1: Is the given, matrix Invertible 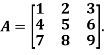
Solution:
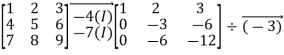
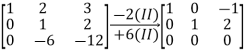
A fail to be invertible, since rref(A)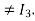
Example 2:
Given 3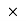 3 Rectangular Matrix
3 Rectangular Matrix
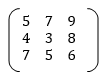
The augumented matrix is as follows
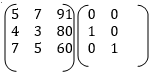
After applying the Gauss-Jordan elimination method:
The inverse of a matrix is as follows,
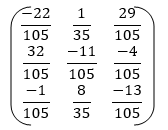
Example 3: Find the inverse of
A= 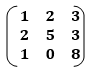
Solution:
Step 1: Adjoin the identity matrix to the right side of A:
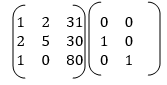
Step 2: Apply row operations to this matrix until the left side is reduced to I. The computations are:
 R2
R2 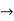 R2-R1 , R3
R2-R1 , R3 R3-R1
R3-R1
 R3
R3  R3 + 2R2
R3 + 2R2
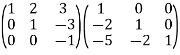 R1
R1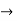 R1 -3R3 , R2
R1 -3R3 , R2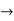 R2+3R3
R2+3R3
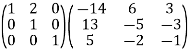 R1
R1 R1-2R2
R1-2R2
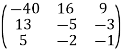
Step 3: Conclusion: The inverse matrix is:
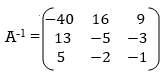
Example 4: Find the inverse of matrix A given below:
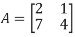
Solution: Let A = IA
Or
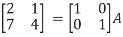

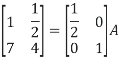
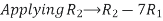
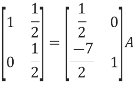
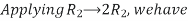

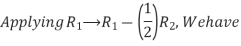
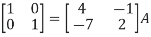
Thus the inverse of matrix A is given by I =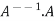
Therefore,

The composition of linear maps is linear: if f : V → W and g : W → Z are linear, then so is their composition g ∘ f : V → Z. It follows from this that the class of all vector spaces over a given field K, together with K -linear maps as morphisms, forms a category. The inverse of a linear map, when defined, is again a linear map.
Example 1: Theorem: Let (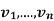 ) be a basis of V and (
) be a basis of V and (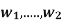 ) an arbitrary list of vectors in W. Then there exists a unique linear map
) an arbitrary list of vectors in W. Then there exists a unique linear map

Proof:
First we verify that there is at most one linear map T with 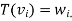 . Take any
. Take any 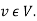 Since (
Since (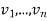 ) is a basis of V there are unique scalars
) is a basis of V there are unique scalars 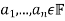 such that
such that 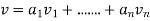 . By linearity we must have
. By linearity we must have

And hence T(v) is completely determined. To show existence , use (3) to define T. It remains to show that this T is linear and that . These two conditions are not hard to show and are left to the reader.
. These two conditions are not hard to show and are left to the reader.
The set of linear maps  is itself a vector space. For S,T
is itself a vector space. For S,T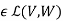 addition is defined as
addition is defined as
(S+T)v = S v + Tv 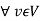
For a 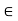 F an T
F an T  scalar multiplication is defined as
scalar multiplication is defined as
(aT)(v) = a(Tv) 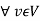
We should verify that S+T and aT are indeed linear maps again and that all properties of a vector space is satisfied.
I.e., associativity, identity and distributive property. Hence by the above properties we conclude that the given transformation is linear transformation.
Example 2: consider a linear map Tv: 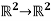 which rotates vectors be an angle 0
which rotates vectors be an angle 0 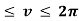 . From a known statement we have the corresponding matrix for this linear transformation is given below, solve for linear mapping
. From a known statement we have the corresponding matrix for this linear transformation is given below, solve for linear mapping
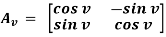
Solution: the composition of two rotations b angles are given by v and v’ that is
TV’TV is clearly the rotation TV+V’ hence we must have
Av+v’ = Av’Av
The left hand side of this equation is given by

And the right hand-side is,
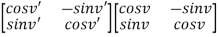
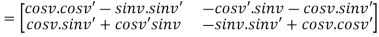
Comparing corresponding entries we find the claim that Tv’Tv = Tv+v’ is equivalent to well-known addition formulas
Cos(v+v’) = cosv. Cosv’ – sinv. Sinv’
Sin(v+v’) = cosv’. Sinv +cosv. Sinv’.
Let V and W be a finite dimensional F- vector spaces such that dimV = n and dimW = m and let BV = 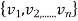 be a basis of V and BW =
be a basis of V and BW = 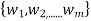 be a basis of W. Let T
be a basis of W. Let T 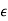 L(V, W)such that for each k = 1,2,…,n we have T (vk) =
L(V, W)such that for each k = 1,2,…,n we have T (vk) =  .then the matrix of linear map T w.r.to the bases BV and BW is
.then the matrix of linear map T w.r.to the bases BV and BW is
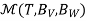 =
= 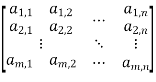
Example 1: Let T 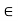 L
L 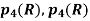 be defined by T(p(x)) = 2xp’(x), and let B1 =
be defined by T(p(x)) = 2xp’(x), and let B1 = 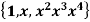 be a basis of
be a basis of 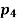 (R). Determine
(R). Determine 
Solution: First we will calculate the images of the basis vectors in B1 under the linear transformation T.
 T(1) = 2x(1)’ = 2x(0) = 0(1) + 0(x) + 0(x2) + 0(x3) + 0(x4)
T(1) = 2x(1)’ = 2x(0) = 0(1) + 0(x) + 0(x2) + 0(x3) + 0(x4)
 T(x) = 2x(x)’ = 2x(1) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
T(x) = 2x(x)’ = 2x(1) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
 T(x2) = 2x(x2)’ = 2x(2x) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
T(x2) = 2x(x2)’ = 2x(2x) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
 T(x3) = 2x(x3)’ = 2x(3x3) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
T(x3) = 2x(x3)’ = 2x(3x3) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
 T(x4) = 2x(x4)’ = 2x (4x3) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
T(x4) = 2x(x4)’ = 2x (4x3) = 0(1) +0(x) + 0(x2) + 0(x3) + 0(x4)
Therefore, we can now construct our matrix as follows.
The first column of 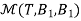 corresponds to the co-efficients determinend by T(1).
corresponds to the co-efficients determinend by T(1).
The second column corresponds to the co-efficients determined by T(x) and so fourth,
 =
= 
Example 2:Let T 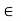 L(M22, M22) be defined by T
L(M22, M22) be defined by T 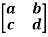 =
=  for a,b,c,d
for a,b,c,d  R and let B1 =
R and let B1 = 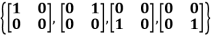 be a basis of M22.Determine
be a basis of M22.Determine 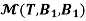
Solution: we will first calculate the images of our basic vectors under T.
T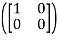 =
= 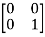 = 0
= 0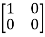 + 0
+ 0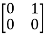 + 0
+ 0 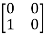 + 1
+ 1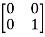
T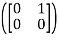 =
=  = 0
= 0 -1
-1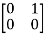 + 0
+ 0 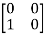 + 0
+ 0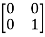
T 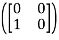 =
= 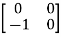 = 0
= 0 + 0
+ 0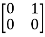 -1
-1 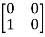 + 0
+ 0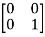
T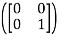 =
= 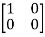 = 1
= 1 + 0
+ 0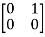 + 0
+ 0 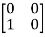 +0
+0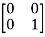
Therefore, we construct
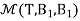 =
= 
References:
1. D. Poole, Linear Algebra: A Modern Introduction, 2nd Edition, Brooks/Cole, 2005.
2. V. Krishnamurthy, V.P. Mainra And J.L. Arora, An Introduction to Linear Algebra, Affiliated East–West Press, Reprint 2005.
3. Erwin Kreyszig, Advanced Engineering Mathematics, 9th Edition, John Wiley & Sons, 2006.
4. Veerarajan T., Engineering Mathematics for First Year, Tata McGraw-Hill,
New Delhi, 2008.
5. N.P. Bali and Manish Goyal, A Text Book of Engineering Mathematics, Laxmi Publications, Reprint, 2010.