Unit – 5
First Order Ordinary Differential Equations
Introduction-
In many engineering problems, differential equations have very important and significant role.
In this unit we will consider differential equations of first order and their solutions.
We study the solutions of differential equations which are: variables separable, homogeneous, non-homogeneous, exact, non-exact using integrating factors, linear, Bernoulli, higher degree, Clairaut’s, Lagrange’s. We consider geometrical applications and physical problems of law of natural growth, natural decay, Newton’s law of cooling, velocity of escape from earth and simple electrical circuits.
A “differential equation” (D.E.) is an equation involves an unknown function y of one or more independent variables x, t , . . . And its derivatives.
Differential equations are classified into two categories “ordinary and partial” depending on the number of independent variables appearing in the equation.
An ordinary differential equation is a D.E. In which the dependent variable y depends only on one independent variable say x (so that the derivatives of y are ordinary derivatives).
Definition-
An exact differential equation is formed by differentiating its solution directly without any other process,
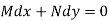
Is called an exact differential equation if it satisfies the following condition-
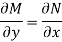
Here 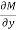 is the differential co-efficient of M with respect to y keeping x constant and
is the differential co-efficient of M with respect to y keeping x constant and 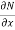 is the differential co-efficient of N with respect to x keeping y constant.
is the differential co-efficient of N with respect to x keeping y constant.
Step by step method to solve an exact differential equation-
1. Integrate M w.r.t. x keeping y constant.
2. Integrate with respect to y, those terms of N which do not contain x.
3. Add the above two results as below-
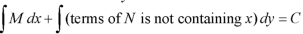
Example-1: Solve 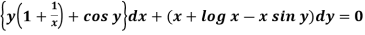
Sol.
Here M = 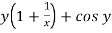 and N =
and N = 
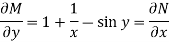
Then the equation is exact and its solution is-
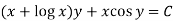
Example-2: Solve-
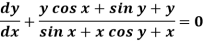
Sol. We can write the equation as below-
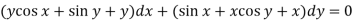
Here M = 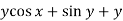 and N =
and N = 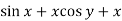
So that-
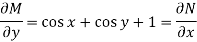
The equation is exact and its solution will be-
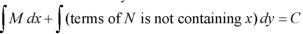
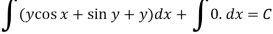
Or

Example-3: Determine whether the differential function ydx –xdy = 0 is exact or not.
Solution. Here the equation is the form of M(x , y)dx + N(x , y)dy = 0
But, we will check for exactness,

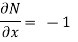
These are not equal results, so we can say that the given diff. Eq. Is not exact.
Example: Solve (5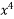 + 3
+ 3 – 2x
– 2x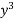 ) dx + (2
) dx + (2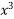 y – 3
y – 3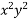 – 5
– 5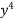 ) dy = 0
) dy = 0
Solution: Here, M = 5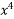 + 3
+ 3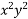 – 2x
– 2x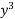 , N = 2
, N = 2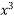 y – 3
y – 3 – 5
– 5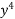

Since, 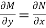 the given equation is exact.
the given equation is exact.
Now 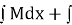 (terms
(terms 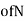 is not containing
is not containing  )
)  (y constant)
(y constant)
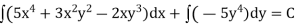
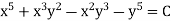 Ans
Ans
Example: Solve: 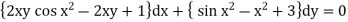
Solution: Here we have
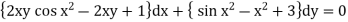 (1)
(1)
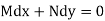 (2)
(2)
Comparing (1) and (2), we get
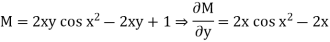
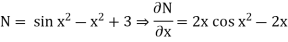
Here, 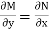
So the given differential equation is exact differential equation.
Hence solution is 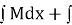 (terms
(terms 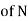 is not containing
is not containing 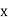 )
) 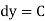



Put 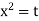 so that
so that 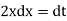
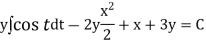

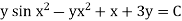 ans
ans
Example: Solve
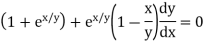
Solution: We 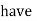
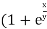 )
) 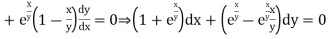
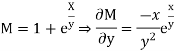

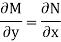
Given equation is exact.
Its solution is 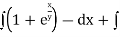 (terms
(terms  not containing
not containing 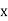 )
) 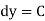
 Ans
Ans
Example: Solve: 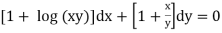
Solution: 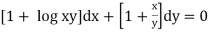

Which is in the form 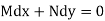
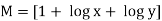 and
and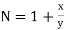
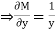 and
and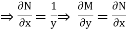
Hence the given differential equation is exact.
Solution is 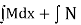 (terms not containing x)
(terms not containing x) 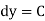

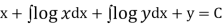 ... (1)
... (1)
Now, 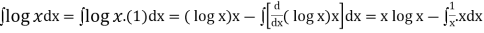
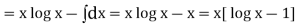
Equation (1) becomes 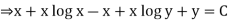
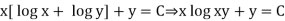
Equation reducible to exact form-
1. If M dx + N dy = 0 be an homogenous equation in x and y, then 1/ (Mx + Ny) is an integrating factor.
Example: Solve-
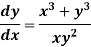
Sol.
We can write the given equation as-
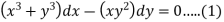
Here,
M = 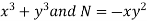

Multiply equation (1) by  we get-
we get-

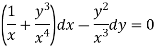
This is an exact differential equation-
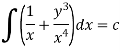

2. I.F. For an equation of the type 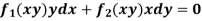
IF the equation Mdx + Ndy = 0 be this form, then 1/(Mx – Ny) is an integrating factor.
Example: Solve-
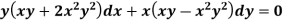
Sol.
Here we have-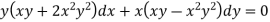
Now divide by xy, we get-
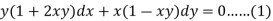
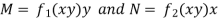
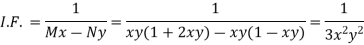
Multiply (1) by 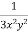 , we get-
, we get-

Which is an exact differential equation-
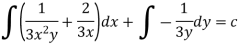
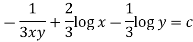
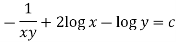
3. In the equation M dx + N dy = 0,
(i) If 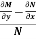 be a function of x only = f(x), then
be a function of x only = f(x), then 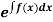 is an integrating factor.
is an integrating factor.
(ii) If 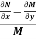 be a function of y only = F(x), then
be a function of y only = F(x), then 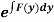 is an integrating factor.
is an integrating factor.
Example: Solve-
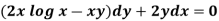
Sol.
Here given,
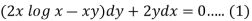
M = 2y and N = 2x log x - xy
Then-
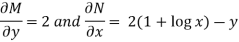
Here,
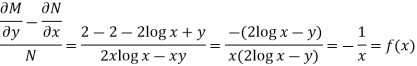
Then,
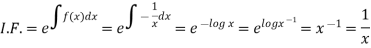
Now multiplying equation (1) by 1/x, we get-
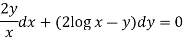
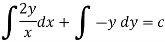
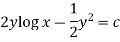
4. For the following type of equation-

An I.F. Is 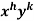
Where-
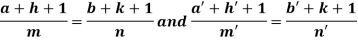
Example: Solve-
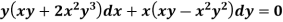
Sol.
We can write the equation as below-
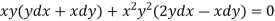
Now comparing with-
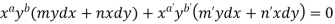
We get-
a = b = 1, m = n = 1, a’ = b’ = 2, m’ = 2, n’ = -1
I.F. = 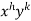
Where-
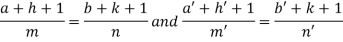
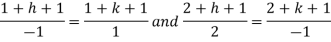
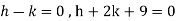
On solving we get-
h = k = -3
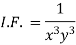
Multiply the equation by 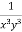 , we get-
, we get-
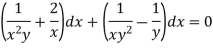
It is an exact equation.
So that the solution is-

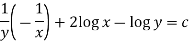
Linear Equations
A differential equation is said to be linear if the dependent variable and its differential coefficients occur only in the first degree and not multiplied together.
Thus the standard form of the linear equation of the first order, commonly known as L eibnitz’s linear equation is

To solve the equation, multiply both sides bi 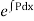
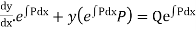 i.e.
i.e. 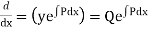
Integrating both sides we get,  as the required solutuion.
as the required solutuion.
Obs. The factor 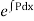 on multiplying by which the left hand side of (1) becomes the differential coefficient of the single function, is called the integrating factor (I.F.) of the linear equation (1)
on multiplying by which the left hand side of (1) becomes the differential coefficient of the single function, is called the integrating factor (I.F.) of the linear equation (1)
It is important to remember that (I.F.)=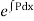
And the solution is 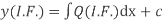
Example. Solve 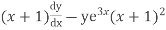
Solution. Dividing throughout by (x+1),given equation becomes
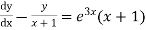 which is Leibnitz’s equation
which is Leibnitz’s equation
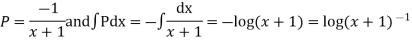

Thus the solution of (1) is 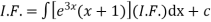
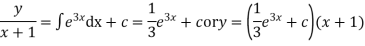
Example. Solve 
Solution. Given solution can be written as 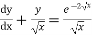
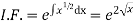
Thus solution of (1) is 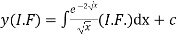
Or, 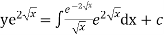
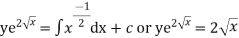
Example. Solve 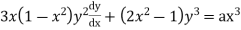
Solution. Putting 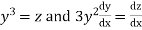 the given equation becomes
the given equation becomes
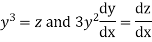
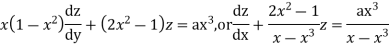
Which is Leibnitz’s equation in z.
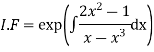
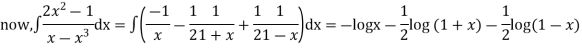
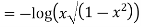
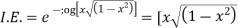
Thus the solution of (1) is

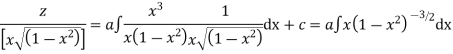

Hence the solution of the given equation is
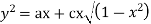
Example. Solve 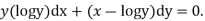
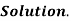 We have
We have 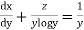 , which is a Leibnitz’sEquation in x
, which is a Leibnitz’sEquation in x
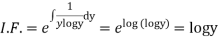
Thus the solution of (1) is 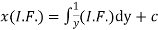
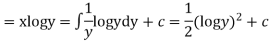
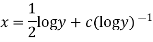
Example. Solve 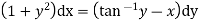
Solution. This equation contains 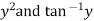 and is therefore not a linear in y, but since only z occurs, it can be written as
and is therefore not a linear in y, but since only z occurs, it can be written as
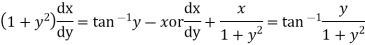
Which is a Leibnitz’s equation in z.

Thus the solution is 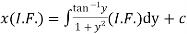
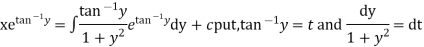

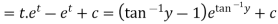
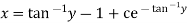
Bernoulli’s equation-
The equation
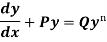
Is reducible to the Leibnitz’s linear equation and is usually called Bernoulli’s equation.
Working procedure to solve the Bernoulli’s linear equation-
Divide both sides of the equation -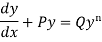
By , so that
, so that
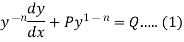
Put 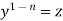 so that
so that 
Then equation (1) becomes-
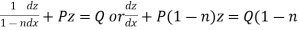 )
)
Here we see that it is a Leibnitz’s linear equations which can be solved easily.
Example: Solve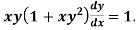
Sol.
We can write the equation as-
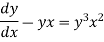
On dividing by 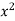 , we get-
, we get-
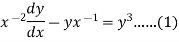
Put 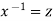 so that
so that 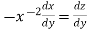
Equation (1) becomes,
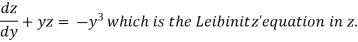
Here,
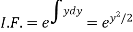
Therefore the solution is-
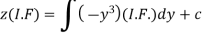
Or
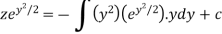
Now put 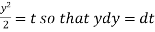
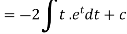
Integrate by parts-
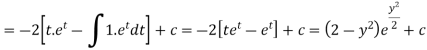
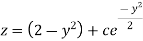
Or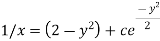
Example. Solve 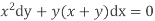
Solution. We have, 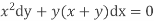
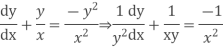
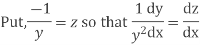
The given equation reduces to a linear differential equation in z.
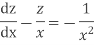
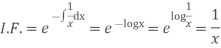
Hence the solution is
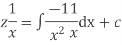

Example. Solve 
Solution. 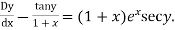
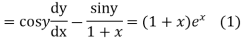

Equation (1) becomes
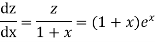
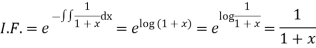
Solution is
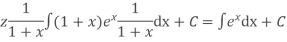

Example: Solve 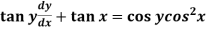
Sol. Here given,
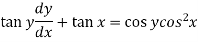

Now let z = sec y, so that dz/dx = sec y tan y dy/dx
Then the equation becomes-
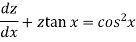
Here,
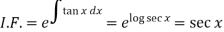
Then the solution will be-
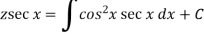
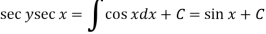
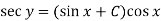
Example: Solve- 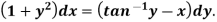
Sol. Here given-

We can re-write this as-

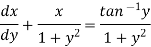
Which is a linear differential equation-
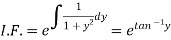
The solution will be-
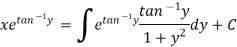
Put 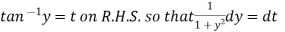
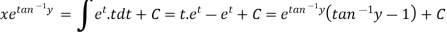
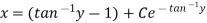
The general first order differential equation
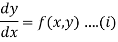
With the initial condition 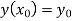
In this method the solution is in the form of a tabulated values.
Integrating both side of the equation (i) we get
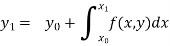
Assuming that 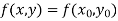 in
in 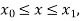 this gives Euler’s formula
this gives Euler’s formula
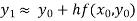
In general formula
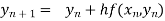 , n=0,1,2,…..
, n=0,1,2,…..
Error estimate for the Euler’s method
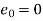
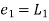
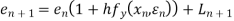
Example1: Use Euler’s method to find y(0.4) from the differential equation
 with h=0.1
with h=0.1
Given equation 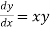
Here 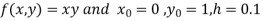
We break the interval in four steps.
So that 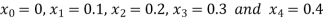
By Euler’s formula
 , n=0,1,2,3 ……(i)
, n=0,1,2,3 ……(i)
For n=0 in equation (i) we get
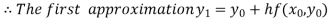
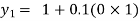
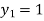
For n=1 in equation (i) we get
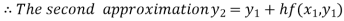
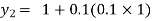
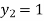 .01
.01
For n=2 in equation (i) we get
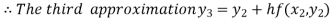
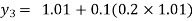
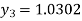
For n=3 in equation (i) we get
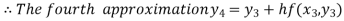
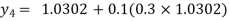

Hence y(0.4) =1.061106.
Example2: Using Euler’s method solve the differential equation for y at x=1 in five steps
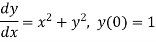
Given equation 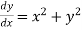
Here 
No. Of steps n=5 and so that 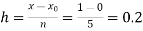
So that 
Also 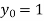
By Euler’s formula
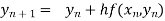 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
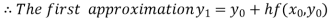
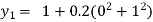
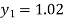
For n=1 in equation (i) we get
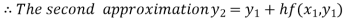
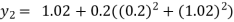
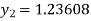
For n=2 in equation (i) we get
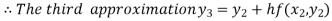
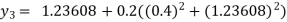
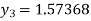
For n=3 in equation (i) we get

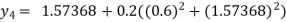

For n=4 in equation (i) we get
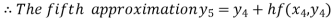
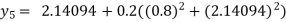
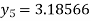
Hence 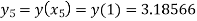
Example3: Given 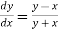 with the initial condition y=1 at x=0.Find y for x=0.1 by Euler’s method(five steps).
with the initial condition y=1 at x=0.Find y for x=0.1 by Euler’s method(five steps).
Given equation is 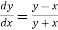
Here 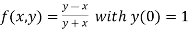
No. Of steps n=5 and so that 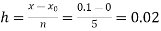
So that 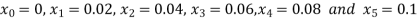
Also 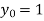
By Euler’s formula
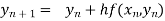 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
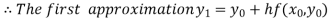
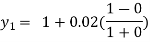

For n=1 in equation (i) we get

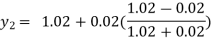
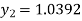
For n=2 in equation (i) we get
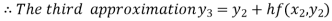
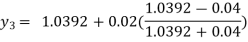
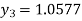
For n=3 in equation (i) we get
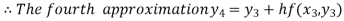
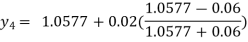
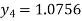
For n=4 in equation (i) we get
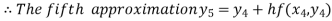
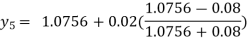
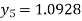
Hence 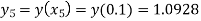
Modified Euler’s Method:
Instead of approximating 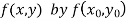 as in Euler’s method. In the modified Euler’s method we have the iteration formula
as in Euler’s method. In the modified Euler’s method we have the iteration formula
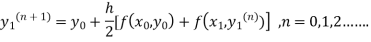
Where  is the nth approximation to
is the nth approximation to 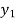 .The iteration started with the Euler’s formula
.The iteration started with the Euler’s formula
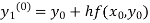
Example1: Use modified Euler’s method to compute y for x=0.05. Given that
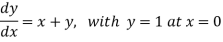
Result correct to three decimal places.
Given equation 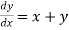
Here 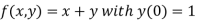
Take h =  = 0.05
= 0.05
By modified Euler’s formula the initial iteration is
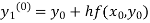
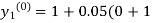 )
)

The iteration formula by modified Euler’s method is
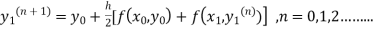 -----(i)
-----(i)
For n=0 in equation (i) we get


Where 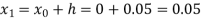 and
and 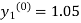 as above
as above
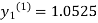
For n=1 in equation (i) we get
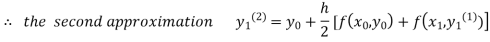

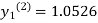
For n=3 in equation (i) we get
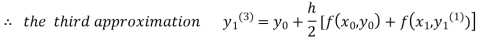
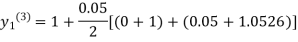
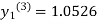
Since third and fourth approximation are equal .
Hence y=1.0526 at x = 0.05 correct to three decimal places.
Example2: Using modified Euler’s method, obtain a solution of the equation

Given equation 
Here 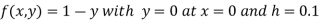
By modified Euler’s formula the initial iteration is
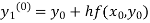
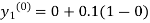

The iteration formula by modified Euler’s method is
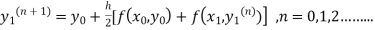 -----(i)
-----(i)
For n=0 in equation (i) we get
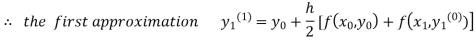
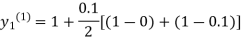
Where 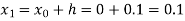 and
and 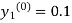 as above
as above
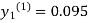
For n=1 in equation (i) we get
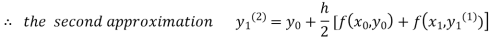
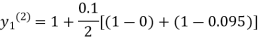
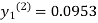
For n=2 in equation (i) we get
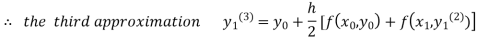

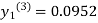
For n=3 in equation (i) we get
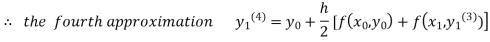
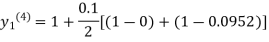
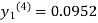
Since third and fourth approximation are equal.
Hence y=0.0952 at x=0.1
To calculate the value of  at x=0.2
at x=0.2
By modified Euler’s formula the initial iteration is
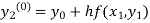

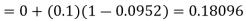
The iteration formula by modified Euler’s method is
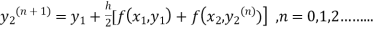 -----(ii)
-----(ii)
For n=0 in equation (ii) we get

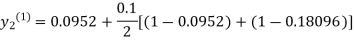
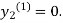 1814
1814
For n=1 in equation (ii) we get
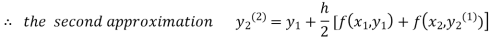
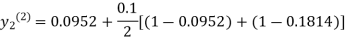
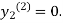 1814
1814
Since first and second approximation are equal .
Hence y = 0.1814 at x=0.2
To calculate the value of 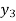 at x=0.3
at x=0.3
By modified Euler’s formula the initial iteration is
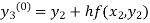

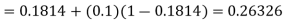
The iteration formula by modified Euler’s method is
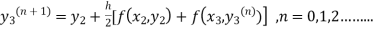 -----(iii)
-----(iii)
For n=0 in equation (iii) we get
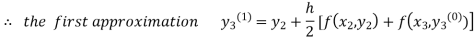
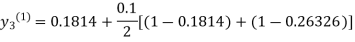
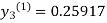
For n=1 in equation (iii) we get
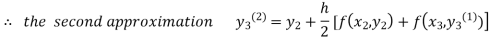

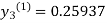
For n=2 in equation (iii) we get
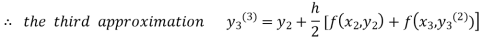
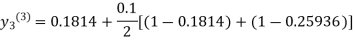
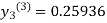
For n=3 in equation (iii) we get
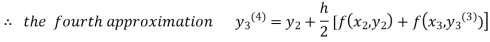
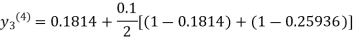
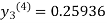
Since third and fourth approximation are same.
Hence y = 0.25936 at x = 0.3
The differential equation will involve 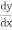 in higher degree and
in higher degree and 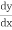 will not denoted by p. The differential equation will be of the form
will not denoted by p. The differential equation will be of the form 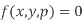
Case 1. Equations solvable for p
Example. Solve 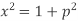
Solution. 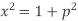
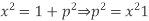
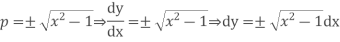
Which gives on integration 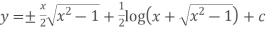
Example. Solve 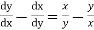
Solution. Given equation is 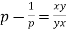 where
where 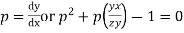
Factorizing, 
Thus we have 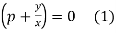

From (1) 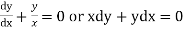
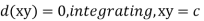
From (2) 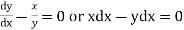
Integrating, 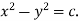 Thus x y=c or
Thus x y=c or  , constitute the required solution.
, constitute the required solution.
Otherwise combining these into one, the required solution can be written as
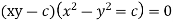
Example. Solve 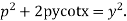
Solution. We have 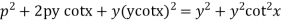
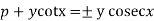

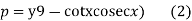
From (1) 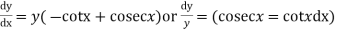
Integrating, 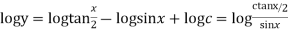
 or,
or, 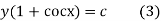
From (2) 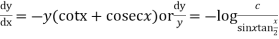
Integrating 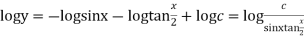
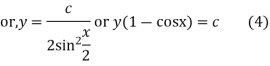
Thus combining (3) and (4), the required general solution is
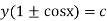
Case II. Equation solvable by y
(i) Differentiate the given equation with respect to x.
(ii) Eliminate p from the given equation and the equation obtained as above.
(iii) The eliminant is the required solution.
Example. Solve. 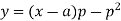
Solution. 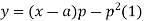
Differentiating (1) with respect to x we obtain
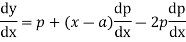
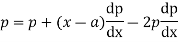
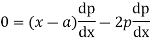
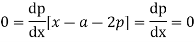
On integration we get p=c
Putting the value of p in (1) we get
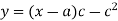
Example. Solve 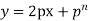
Solution. 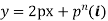
Differentiating it with respect to x we get
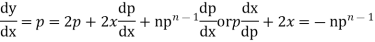
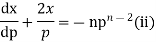
This is Leibnitz’s linear equation in x and p. Here 
Therefore the solution of (ii) is
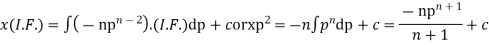
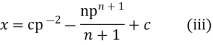
Substituting this value of x in (i) we get 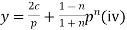
The equations (iii) and (iv) taken together with parameter p constitute the general solution (i).
Case III. Equations solvable by x.
(i) Differentiate the given equation with respect to y.
(ii) Solve the equation as obtained in (1) for p.
(iii) Eliminate p by putting the value of p in the given equation.
(iv) The eliminant is the required solution.
Example. Solve 
Solution. 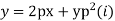
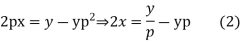
Differentiating (2) with respect to x we get
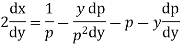
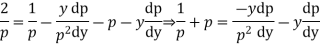
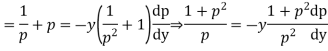
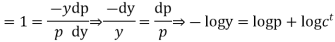
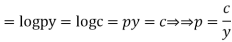
Putting the value of p in (1)
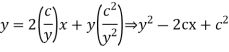
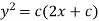
Example. Solve 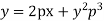
Solution. Given equation on solving for x takes the form x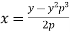
Differentiating with respect to y, 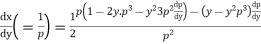
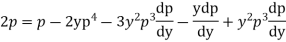
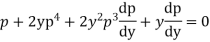
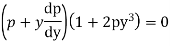
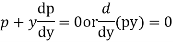
Integrating, 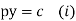
Thus eliminating from the given equation and (i) we get  which is required solution.
which is required solution.
Class IV. Clairaut’s equation
The equation 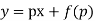 is known as Clairaut equation
is known as Clairaut equation
Differentiating (1) with respect to x
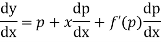
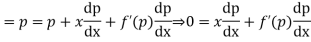
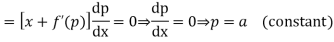
Putting the value of p in (1) we have
y=ax+f(a)
Which is the required solution.
Method. In the Clairaut equation, on replacing p by a constant, we get the solution of the problem.
Example. Solve. 
Solution. 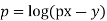 or
or 
Which is Clairaut equation.
Here its solution is 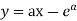
Example. Solve 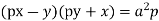
Solution. Put, 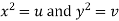 so that
so that 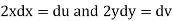
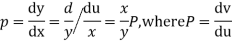
Then the given equation becomes 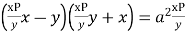
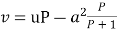 which is Clairaut form and its solution is
which is Clairaut form and its solution is 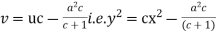
References:
- G.B. Thomas And R.L. Finney, Calculus And Analytic Geometry, 9th Edition, Pearson, Reprint, 2002.
- Erwin Kreyszig, Advanced Engineering Mathematics, 9th Edition, John Wiley & Sons, 2006.
- W. E. Boyce And R. C. Diprima, Elementary Differential Equations And Boundary
- Value Problems, 9th Edition, Wiley India, 2009.
- S. L. Ross, Differential Equations, 3rd Ed., Wiley India, 1984.
- E. A. Coddington, An Introduction To Ordinary Differential Equations, Prentice Hall India, 1995.
- E. L. Ince, Ordinary Differential Equations, Dover Publications, 1958.
1 J. W. Brown And R. V. Churchill, Complex Variables And Applications, 7th Ed., Mc- Graw Hill, 2004.
2 N.P. Bali And Manish Goyal, A Text Book Of Engineering Mathematics, Laxmi Publications, Reprint, 2008.
3 B.S. Grewal, Higher Engineering Mathematics, Khanna Publishers, 36th Edition, 2010.
4 Hk dass