Unit - 4
Reasoning Under Inconsistencies and Uncertainties
Monotonic Reasoning:
In monotonic reasoning, once the conclusion is taken, then it will remain the same even if we add some other information to existing information in our knowledge base. In monotonic reasoning, adding knowledge does not decrease the set of prepositions that can be derived.
To solve monotonic problems, we can derive the valid conclusion from the available facts only, and it will not be affected by new facts.
Monotonic reasoning is not useful for the real-time systems, as in real time, facts get changed, so we cannot use monotonic reasoning.
Monotonic reasoning is used in conventional reasoning systems, and a logic-based system is monotonic.
Any theorem proving is an example of monotonic reasoning.
Example:
Earth revolves around the Sun.
It is a true fact, and it cannot be changed even if we add another sentence in knowledge base like, "The moon revolves around the earth" Or "Earth is not round," etc.
Advantages of Monotonic Reasoning:
● In monotonic reasoning, each old proof will always remain valid.
● If we deduce some facts from available facts, then it will remain valid for always.
Disadvantages of Monotonic Reasoning:
● We cannot represent the real world scenarios using Monotonic reasoning.
● Hypothesis knowledge cannot be expressed with monotonic reasoning, which means facts should be true.
● Since we can only derive conclusions from the old proofs, so new knowledge from the real world cannot be added.
Non-monotonic Reasoning
In Non-monotonic reasoning, some conclusions may be invalidated if we add some more information to our knowledge base.
Logic will be said as non-monotonic if some conclusions can be invalidated by adding more knowledge into our knowledge base.
Non-monotonic reasoning deals with incomplete and uncertain models.
"Human perceptions for various things in daily life, "is a general example of non-monotonic reasoning.
Example: Let suppose the knowledge base contains the following knowledge:
● Birds can fly
● Penguins cannot fly
● Pitty is a bird
So from the above sentences, we can conclude that Pitty can fly.
However, if we add one another sentence into knowledge base "Pitty is a penguin", which concludes "Pitty cannot fly", so it invalidates the above conclusion.
Advantages of Non-monotonic reasoning:
● For real-world systems such as Robot navigation, we can use non-monotonic reasoning.
● In Non-monotonic reasoning, we can choose probabilistic facts or can make assumptions.
Disadvantages of Non-monotonic Reasoning:
● In non-monotonic reasoning, the old facts may be invalidated by adding new sentences.
● It cannot be used for theorem proving.
Key takeaway
In monotonic reasoning, once the conclusion is taken, then it will remain the same even if we add some other information to existing information in our knowledge base.
In Non-monotonic reasoning, some conclusions may be invalidated if we add some more information to our knowledge base.
Truth Maintenance Systems (TMS), also known as Reason Maintenance Systems, are used in Problem Solving Systems to manage the inference engine's beliefs in given sentences as a Dependency Network, in conjunction with Inference Engines (IE) such as rule-based inference systems.
PROBLEM SOLVING SYSTEM
+--------------------------------------------+
| |
| +----+ +-----+ |
| | IE |<---------------->| TMS | |
| +----+ +-----+ |
| |
+--------------------------------------------+
Truth Maintenance Systems: To implement Non-Monotonic Reasoning Systems, a number of Truth Maintenance Systems (TMS) have been created.
TMSs are, in a nutshell:
● All of them employ some type of dependency-directed backtracking,
● in which assertions are linked by a web of dependencies.
Characteristics
The following are some of the properties of Truth Maintenance Systems:
Justification-Based Truth Maintenance Systems (JTMS)
● This is a basic TMS because it has no knowledge of the structure of the statements themselves.
● There is a reason for each supported belief (assertion).
● Each justification is divided into two parts:
○ An IN-List is a list of beliefs that a person holds.
○ An OUT-List — a group of people who believe in something they don't believe in.
● An arrow connects an assertion to its justification.
● The network is formed when one statement feeds another reason.
● A belief status can be assigned to assertions.
● If every assertion in the IN-List is believed but none in the OUT-List, the assertion is legitimate.
● If the OUT-List is not empty or if any assertion in the IN-List is non-monotonic, the assertion is non-monotonic.
Logic-Based Truth Maintenance Systems (LTMS):
Identical to JTMS, with the following exceptions:
● Nodes (assertions) are assumed to have no ties between them until those relationships are expressly mentioned in reasons.
● JTMS can represent both P and P at the same time. An LTMS would result in a contradiction in this case.
● If this occurs, the network must be rebuilt.
Assumption-Based Truth Maintenance Systems (ATMS)
● JTMS and LTMS pursue a single line of reasoning at a time, and when necessary, retrace (dependency-directed) — depth first search.
● ATMs keep two paths open in parallel: breadth-first search and depth-first search.
● Backtracking is avoided at the expense of numerous contexts being maintained.
● However, as the reasoning progresses, inconsistencies emerge, and the ATMS can be trimmed.
● Simply look for assertions that aren't supported by evidence.
Key takeaway
Truth Maintenance Systems (TMS), also known as Reason Maintenance Systems, are used in Problem Solving Systems to manage the inference engine's beliefs in given sentences as a Dependency Network, in conjunction with Inference Engines (IE) such as rule-based inference systems.
Default reasoning is a type of Defeasible Reasoning that is used to convey facts such as "something is true by default."
Raymond Reiter introduced Default Logic as a Non-Monotonic Logic to formalise reasoning with default assumptions.
The only thing that standard logic can express is whether something is true or untrue.
This is an issue since reasoning frequently incorporates facts that are true most of the time but not always.
For instance, "Birds usually fly" vs. "All birds fly."
Penguins and ostriches are exceptions.
To deal with non-monotonicity and belief revision, Default Reasoning (and Default Logic) was developed.
Its primary goal is to formalise default inference rules while omitting all exceptions.
We'd like to know, just as we did previously. We'd like to know if Bobik is a Carnivore based on the following information: is a Carnivore based on the following information:
Dog(Bobik Dog(Bobik).
Assuming we know dogs are carnivores in general. Then there are carnivores, which are carnivores in general. Then, in order to obtain the answer, we'll apply the following formula: To find the solution, we'll use the following formula:
Given that a P is generally a Q, and given that P(a) is true, it is reasonable to infer that) is true, it is fair to conclude that Q(a) is true unless there is a strong reason not to. Unless there is a compelling reason not to, is correct.
Since the term was coined, the definition is a little hazy. Because the "excellent reason good reason" element isn't stated, the definition is a little hazy. We do not, however, have a specified part. However, we frequently rely on default reasoning: Default reasoning is frequently used:
If we were asked to describe the colour of a polar bear, we would say If we were asked to describe the colour of a polar bear, we would say
By default, the response would be By default, the answer is – white.
If we find out that the current bear has If we find out that the current bear has been rolling in mud, we might reconsider our position.
Logics formalizing default reasoning
Logics that can handle arbitrary default assumptions (default logic, defeasible reasoning, and answer set programming).
Logics that define the special default assumption that unknown facts can be assumed untrue by default (closed world assumption and circumscription).
Syntax of default logic
A pair < D,W> is a default theory.
The backdrop theory is a set of logical equations that formalises the facts that are known for sure.
D is a set of default rules, each of which has the following format:
Prerequisite: Justification1, …,Justificationn
Conclusion
We are driven to believe that Conclusion is true if we believe that Prerequisite is true and that each of Justification is consistent with our present views.
The logical formulae in W, as well as all formulas in a default, were considered to be first-order logic formulae at first, but they might be formulae in any formal logic.
Closed world assumption
Assumption of a closed world In artificial intelligence, a method for dealing with incompleteness. All facts are assumed to be true or untrue in a logic knowledge base. Any things with unknown truth values can't be represented without making some uncomfortable changes. The closed-world assumption addresses this by assuming that anything outside the knowledge base is untrue; in other words, unknown is the same as false.
In a formal system of logic used for knowledge representation, the closed-world assumption (CWA) is the assumption that a statement that is true is also known to be true. What is not now known to be true, on the other hand, is false. The same name also refers to Raymond Reiter's logical formalisation of this assumption. The open-world assumption (OWA) is the polar opposite of the closed-world assumption, saying that absence of knowledge does not indicate untruth. The interpretation of the real semantics of a conceptual statement with the identical notations of ideas is determined by CWA vs. OWA decisions. In most cases, a successful formalisation of natural language semantics will reveal whether the implicit logical foundations are based on CWA or OWA.
Negation as failure is linked to the closed-world assumption since it entails believing untrue every predicate that cannot be proven true.
The simplest way to express default is to use the word "default." Closed world reasoning is the most basic formalisation of default thinking. Closed world reasoning is a type of reasoning.
Observation:
The number of bad information concerning a specific topic. The amount of negative facts about a domain is often substantially more than the number of good facts about the domain. a large number of them are positive.
In many natural applications, the number of possible outcomes is limited. The quantity of explicit negative facts in many natural applications is so huge that their explicit representation becomes practically unfeasible. It becomes nearly impossible to represent yourself.
Example
A lending – library's data base. Library. Assume there are 1000 and 10,000 readers. Assume there are 1000 readers and 10,000 books, and each reader is permitted to borrow up to five volumes. In order to keep track of all of the books (up to five). We would need to store a tremendous quantity of data to keep track of all readers and all the books they do not currently borrow(the negative facts) currently borrow(the negative facts). a large volume of data
The closed world assumption
The obvious solution to this issue is to The logical solution to this dilemma is to assume that all positive information has been provided, and to conclude that any positive fact that has not been specified or that has not been specified or cannot be inferred from this information is untrue. This knowledge leads to a wrong conclusion.
This is the CWA rule in its entirety. This is the CWA rule in its entirety.
Key takeaway
Default reasoning is a type of Defeasible Reasoning that is used to convey facts such as "something is true by default."
Assumption of a closed world In artificial intelligence, a method for dealing with incompleteness. All facts are assumed to be true or untrue in a logic knowledge base.
Predicate completion is a closed-world reasoning strategy that assumes the stated sufficient conditions on a predicate are also required. An axiom schema realises circumscription, which is a formal device that characterises minimal reasoning, i.e. reasoning in minimal models. The main result of this paper is that the circumscription of P logically implies P's completion axiom for first order theories that are Horn in a predicate P.
A mechanism for "closing off" a first order representation is predicate completion [Clark 1978, Kowalski 19781. This idea comes from the observation that many world descriptions offer sufficient, but not required, conditions on one or more of their predicates, and hence are incomplete world descriptions. When reasoning about such worlds, one frequently uses a common sense reasoning convention that supports the notion - the so-called closed world assumption [Reiter 19781 - that the information presented about a predicate is all and only relevant knowledge about that predicate.
This assumption is formally interpreted by Clark as the assumption that the adequate requirements on the predicate, which are expressly stated by the world description, are also required. Consider the following simple blocks world description to better understand the concept:
A and B are distinct blocks.
A is on the table.
B is on A
These statements naturally convert into the following first-order equality theory, given the availability of general information that blocks cannot be tables:
BLOCK (A) BLOCK (B)
0N (A,TABLE) ON (B,A) (2)
A#B A# TABLE B # TABLE
Although we cannot prove that nothing is on B from (2), i.e. (2) /+ (x> -ON(x,B), there is a common sense convention regarding the description (1) that should allow us to reach this conclusion. According to this convention, (1) is a description of all and only the pertinent information about this world. Consider the equations to demonstrate how Clark interprets this convention.
(x) .x = A V x = B ZJ BLOCK (x) (3)
(xy).x = A 6 y = TABLE V x * B d y = A 3 ON(x,y)
Which are comparable to the facts about the predicate BLOCK and the predicate ON, respectively, in (2). These can be interpreted as the predicates BLOCK and ON's "if halves," or sufficient conditions. The closed world assumption is associated with the notion that these sufficient conditions are likewise required, according to Clark. This assumption can be made explicit by supplementing representation (2) with BLOCK and ON's "only if halves" or necessary conditions:
(x). BLOCK(x) 1 x=A V x=B (xy).
ON (x,y) 3 x=A & y=TABLE V x=B & y=A
These "only if" formulations are referred to by Clark as the completions of the predicates BLOCK and ON, respectively. As a result, under the closed world assumption, the first order representation is
(x). BLOCK(x) : x=A V x=B (xy).
ON(x,y) = x=A & y=TABLE V x=B & y=A AfB
A ≠ B A ≠ TABLE B ≠ TABLE
Nothing is on B - (x)-ON(x,B) - according to this theory, which was not deduced from the original theory.
Circumscription [McCarthy 19801] is a new way of thinking about the difficulty of "closing off" a first-order representation. McCarthy's intuitions about the closed world assumption are largely semantic in nature. For him, statements derivable from a first order theory T under the closed world assumption concerning a predicate P are simply statements true in all T models that are minimum with respect to P. These are models in which P's extension is minimal, roughly speaking. By enhancing T with the following axiom schema, dubbed the circumscription of P in T, McCarthy forces the examination of only such models:
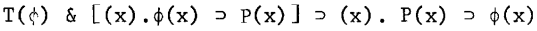
P is an n-ary predicate, and $ is an n-ary predicate parameter in this case. T(Φ) is the result of combining the formulas of T and replacing each occurrence of P with Φ. First order deductions from the theory T, along with this axiom schema, are formally associated with reasoning about the theory T under the closed world assumption about P. The closure of T with respect to P is the extended theory denoted by CLOSUREp(T). Typically, this schema is used to "guess" an appropriate instance of Φ, one that allows anything meaningful to be deduced.
Key takeaway
Predicate completion is a closed-world reasoning strategy that assumes the stated sufficient conditions on a predicate are also required. An axiom schema realises circumscription, which is a formal device that characterises minimal reasoning, i.e. reasoning in minimal models.
Fuzzy Logic (FL) is that of a method of the reasoning that resembles human reasoning. The approach of the FL imitates the way of decision making in humans that involves all intermediate possibilities between that of the digital values YES and NO.
The conventional logic block that a computer can understand takes the precise input and produces that of a definite output as TRUE or FALSE, which is equivalent to that of a human’s YES or NO.
The inventor of fuzzy logic, Lotfi Zadeh, observed that unlike the computers, the human decision making includes that of a range of the possibilities between YES and NO, example −
CERTAINLY YES |
POSSIBLY YES |
CANNOT SAY |
POSSIBLY NO |
CERTAINLY NO |
The fuzzy logic works on the levels of that of the possibilities of the input to achieve that of the definite output.
Implementation
● It can be implemented in the systems with the various sizes and the capabilities ranging from that of the small microcontrollers to large, the networked, and the workstation-based control systems.
● It can be implemented in the hardware, the software, or a combination of both.
Why Fuzzy Logic?
Fuzzy logic is useful for commercial and practical purposes.
● It can control the machines and the consumer products.
● It may not give the accurate reasoning, but acceptable to that of the reasoning.
● Fuzzy logic helps to deal with that uncertainty in engineering.
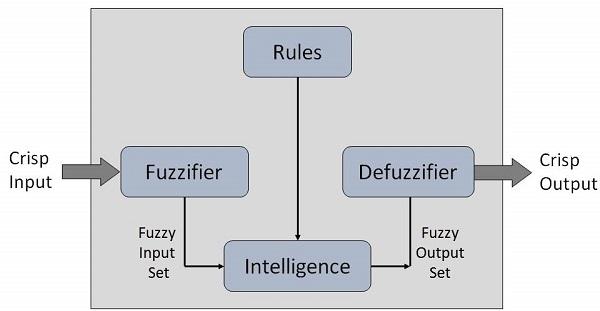
Fuzzy Logic Systems Architecture
It has four main parts as shown below −
● Fuzzification Module − It transforms that of the system inputs, which are crisp numbers, into that of the fuzzy sets. It splits the input signal into five steps example −
LP | x is Large Positive |
MP | x is Medium Positive |
S | x is Small |
MN | x is Medium Negative |
LN | x is Large Negative
|
● Knowledge Base − It stores IF-THEN rules provided by that of the experts.
● Inference Engine − It simulates that of the human reasoning process by making the fuzzy inference on the inputs and IF-THEN rules.
● Defuzzification Module − It transforms the fuzzy set obtained by that of the inference engine into a crisp value.
The membership functions work on that of the fuzzy sets of variables.
Membership Function
Membership functions allow you to quantify that of the linguistic term and represent a fuzzy set graphically. A membership function for that of a fuzzy set A on the universe of that of the discourse X is defined as μA:X → [0,1].
Here, each element of X is mapped to that of a value between 0 and 1. It is called the membership value or that of the degree of membership. It quantifies the degree of that of the membership of the element in X to that of the fuzzy set A.
● x axis represents that of the universe of discourse.
● y axis represents that of the degrees of membership in the [0, 1] interval.
There can be multiple membership functions applicable to that of the fuzzify a numerical value. Simple membership functions are used as use of that of the complex functions does not add more precision in the output.
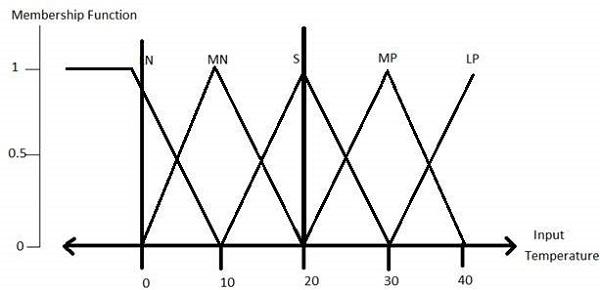
All membership functions for LP, MP, S, MN, and LN are shown as below −
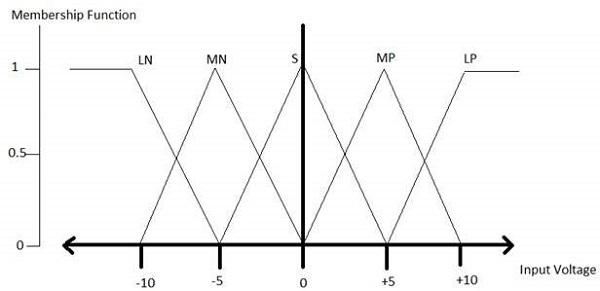
The triangular membership function shapes are the most of the common among various of the other membership function shapes for example trapezoidal, singleton, and Gaussian.
Here, the input to that of the 5-level fuzzifier varies from that of the -10 volts to +10 volts. Hence the corresponding output will also change.
Example of a Fuzzy Logic System
Let us consider that an air conditioning system with that of the 5-level fuzzy logic system. This system adjusts that of the temperature of the air conditioner by comparing that of the room temperature and that of the target temperature value.
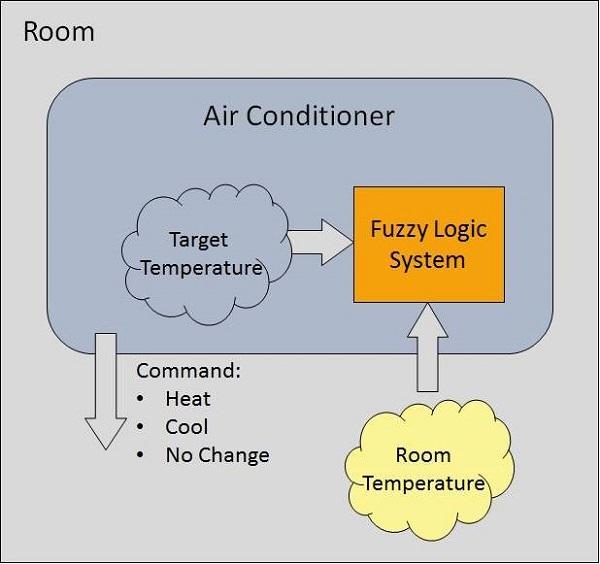
Fig: Example
Algorithm
● Define linguistic Variables and terms (start)
● Construct membership functions for them. (start)
● Construct knowledge base of rules (start)
● Convert crisp data into fuzzy data sets using membership functions. (fuzzification)
● Evaluate rules in the rule base. (Inference Engine)
● Combine results from each rule. (Inference Engine)
● Convert output data into non-fuzzy values. (defuzzification)
Development
Step 1 − Define linguistic variables and terms
Linguistic variables are the input and the output variables in that of the form of the simple words or the sentences. For that of the room temperature, cold, warm, hot, etc., are the linguistic terms.
Temperature (t) = {very-cold, cold, warm, very-warm, hot}
Every member of this set is that of a linguistic term and it can cover that of the some portion of overall temperature of the values.
Step 2 − Construct membership functions for them
The membership functions of temperature variable are as shown −
Step3 − Construct knowledge base rules
Create a matrix of room temperature values versus target temperature values that an air conditioning system is expected to provide.
RoomTemp. /Target | Very_Cold | Cold | Warm | Hot | Very_Hot |
Very_Cold | No_Change | Heat | Heat | Heat | Heat |
Cold | Cool | No_Change | Heat | Heat | Heat |
Warm | Cool | Cool | No_Change | Heat | Heat |
Hot | Cool | Cool | Cool | No_Change | Heat |
Very_Hot | Cool | Cool | Cool | Cool | No_Change |
Build a set of rules into the knowledge base in the form of IF-THEN-ELSE structures.
Sr. No. | Condition | Action |
1 | IF temperature=(Cold OR Very_Cold) AND target=Warm THEN | Heat |
2 | IF temperature=(Hot OR Very_Hot) AND target=Warm THEN | Cool |
3 | IF (temperature=Warm) AND (target=Warm) THEN | No_Change |
Step 4 − Obtain fuzzy value
Fuzzy set operations perform evaluation of rules. The operations used for that of the OR and AND are the Max and Min respectively. Combine all of the results of the evaluation to form that of a final result. This result is that of a fuzzy value.
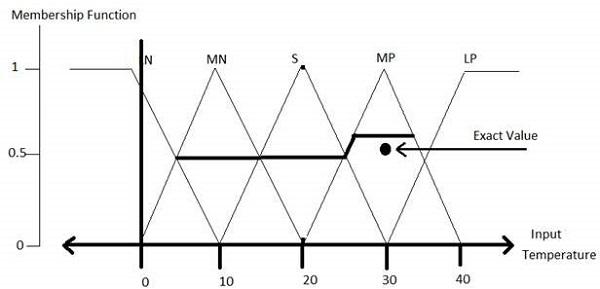
Step 5 − Perform defuzzification
Defuzzification is then performed according to that of the membership function for output variable.
Application Areas of Fuzzy Logic
The key application areas of fuzzy logic are as follows −
Automotive Systems
● Automatic Gearboxes
● Four-Wheel Steering
● Vehicle environment control
Consumer Electronic Goods
● Hi-Fi Systems
● Photocopiers
● Still and Video Cameras
● Television
Domestic Goods
● Microwave Ovens
● Refrigerators
● Toasters
● Vacuum Cleaners
● Washing Machines
Environment Control
● Air Conditioners/Dryers/Heaters
● Humidifiers
Advantages of FLSs
● Mathematical concepts within that of the fuzzy reasoning are very simple.
● You can modify a FLS by just adding or deleting the rules due to the flexibility of fuzzy logic.
● Fuzzy logic Systems can take the imprecise, the distorted, noisy input information.
● FLSs are easy to construct and to understand.
● Fuzzy logic is that of a solution to complex problems in all of the fields of life, including medicine, as it resembles human reasoning and that of the decision making.
Disadvantages of FLSs
● There is no systematic approach to that of fuzzy system designing.
● They are understandable only when they are simple.
● They are suitable for problems which do not need very high accuracy.
Key takeaway
Fuzzy Logic (FL) is that of a method of the reasoning that resembles human reasoning. The approach of the FL imitates the way of decision making in humans that involves all intermediate possibilities between that of the digital values YES and NO.
Calculating the posterior distribution of a query variable given some evidence is the most typical probabilistic inference problem. Unfortunately, estimating the posterior probability in a belief network within an absolute error (less than 0.5) or within a constant multiplicative factor is NP-hard, therefore there will be no universal efficient solutions.
The most common methods for probabilistic inference in belief networks are as follows:
● Taking use of the network's structure The variable elimination algorithm, which will be discussed later, is an example of this strategy.
● techniques based on searching From the worlds formed, posterior probabilities can be determined by enumerating some of the possible worlds. A bound on the error in the posterior probability can be estimated by determining the probability mass of the worlds not considered. When the distributions are severe (all probability are near to zero or one), as they are in engineered systems, this method works effectively.
● The goal of variational inference is to identify a problem approximation that is simple to compute. Choose an easy-to-compute class of representations first. This category could be as simple as a collection of disparate belief networks (with no arcs). Next, look for a member of the class who is the most similar to the original issue. Find an easy-to-compute distribution that is as close to the posterior distribution that must be computed as possible. As a result, the problem is reduced to an optimization problem of error minimization.
● Simulation that is stochastic. Random cases are generated using these methods based on probability distributions. The marginal distribution on any combination of variables can be approximated by treating these random cases as a set of samples.
Causes of uncertainty:
In the real world, the following are some of the most common sources of uncertainty.
● Information occurred from unreliable sources.
● Experimental Errors
● Equipment fault
● Temperature variation
● Climate change.
Probabilistic reasoning is a knowledge representation method that uses the concept of probability to indicate uncertainty in knowledge. We employ probabilistic reasoning, which integrates probability theory and logic, to deal with uncertainty.
Probability is employed in probabilistic reasoning because it helps us to deal with uncertainty caused by someone's indifference or ignorance.
There are many situations in the real world when nothing is certain, such as "it will rain today," "behavior of someone in specific surroundings," and "a competition between two teams or two players." These are probable sentences for which we can presume that something will happen but are unsure, thus we utilize probabilistic reasoning in this case.
Probability: Probability is a measure of the likelihood of an uncertain event occurring. It's a numerical representation of the likelihood of something happening. The probability value is always between 0 and 1, indicating complete unpredictability.
0 ≤ P(A) ≤ 1, where P(A) is the probability of an event A.
P(A) = 0, indicates total uncertainty in an event A.
P(A) =1, indicates total certainty in an event A.
We can compute the probability of an uncertain event using the formula below.
P(¬A) = probability of a not happening event.
P(¬A) + P(A) = 1.
Event: An event is the name given to each conceivable consequence of a variable.
Sample space: Sample space is a collection of all potential events.
Random variables: Random variables are used to represent real-world events and objects.
Prior probability: The prior probability of an occurrence is the probability calculated before fresh information is observed.
Posterior Probability: After all evidence or information has been considered, the likelihood is computed. It's a mix of known probabilities and new information.
Conditional probability: The likelihood of an event occurring when another event has already occurred is known as conditional probability.
Key takeaway
Probabilistic reasoning is a method of knowledge representation in which the concept of probability is used to convey the uncertainty in knowledge.
Probability is used in probabilistic reasoning because it allows us to deal with the uncertainty that arises from someone's laziness or ignorance.
● Bayesian Networks, also known as Bayes Nets, Belief Nets, Causal Nets, and Probability Nets, are a data structure for capturing all of the information in a domain's entire joint probability distribution. The Bayesian Net can compute every value in the entire joint probability distribution of a collection of random variables.
● This variable represents all direct causal relationships between variables.
● To construct a Bayesian net for a given set of variables, draw arcs from cause variables to immediate effects.
● It saves space by taking advantage of the fact that variable dependencies are generally local in many real-world problem domains, resulting in a high number of conditionally independent variables.
● In both qualitative and quantitative terms, the link between variables is captured.
● It's possible to use it to construct a case.
● Predictive reasoning (sometimes referred to as causal reasoning) is a sort of reasoning that proceeds from the top down (from causes to effects).
● From effects to causes, diagnostic thinking goes backwards (bottom-up).
● When A has a direct causal influence on B, a Bayesian Net is a directed acyclic graph (DAG) in which each random variable has its own node and a directed arc from A to B. As a result, the nodes represent states of affairs, whereas the arcs represent causal relationships. When A is present, B is more likely to occur, and vice versa. The backward influence is referred to as "diagnostic" or "evidential" support for A due to the presence of B.
● Each node A in a network is conditionally independent of any subset of nodes that are not children of A, given its parents.
A Bayesian network that depicts and solves decision issues under uncertain knowledge is known as an influence diagram.
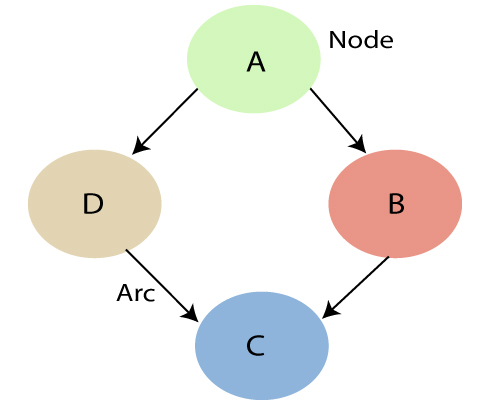
Fig: Bayesian network graph
● Each node represents a random variable that can be continuous or discontinuous in nature.
● Arcs or directed arrows represent the causal relationship or conditional probabilities between random variables. The graph's two nodes are connected by these directed links, also known as arrows.
These ties imply that one node has a direct influence on another, and nodes are independent of one another if there are no directed relationships.
Key takeaway
Bayesian Networks, also known as Bayes Nets, Belief Nets, Causal Nets, and Probability Nets.
Bayesian Networks are a data structure for capturing all of the information in the whole joint probability distribution for the collection of random variables that define a domain.
DST is a mathematical theory of evidence based on belief functions and plausible reasoning. It is used to combine that of the separate pieces of the information (evidence) to calculate that of the probability of an event.
DST offers an alternative to that of the traditional probabilistic theory for that of the mathematical representation of the uncertainty.
DST can be regarded as that of a more general approach to represent the uncertainty than the Bayesian approach.
Bayesian methods are sometimes inappropriate
Example:
Let A represent the proposition "Moore is attractive". Then the axioms of probability insist that P(A) + P(¬A) = 1.
Now suppose that the Andrew does not even know who "Moore" is, then
We cannot say that Andrew believes the proposition if he has no idea what it means.
Also, it is not fair to say that he disbelieves the proposition.
It would therefore be meaningful to denote Andrew's belief B of
B(A) and B(¬A) as both being 0.
Certainty factors do not allow this.
Dempster-Shafer Model
The idea is to allocate a number between 0 and 1 to indicate a degree of belief on a proposal as in the probability framework.
However, it is not considered that of a probability but that of a belief mass. The distribution of that of the masses is known basic belief assignment.
In other words, in this formalism that of a degree of belief (referred as mass) is represented as that of a belief function rather than that of a Bayesian probability distribution.
Example: Belief assignment
Suppose a system has that of a five members, say five independent states, and exactly one of which is the actual. If the original set is called S, |S| = 5, then
The set of all subsets (the power set) is called 2S.
If each possible subset as that of a binary vector (describing any member is present or not by writing 1 or 0), then 25 subsets are possible, ranging from the empty subset ( 0, 0, 0, 0, 0 ) to the "everything" subset ( 1, 1,1, 1, 1 ).
The "empty" subset represents a "contradiction", which is not true in any state, and is thus assigned a mass of one;
The remaining masses are normalized so that their total is 1.
The "everything" subset is labelled as "unknown"; it represents the state where all elements are present one, in the sense that you cannot tell which is actual.
Belief and Plausibility
Shafer's framework allows for belief about propositions to be represented as intervals, bounded by two values, belief (or support) and plausibility:
Belief ≤ plausibility
Belief in a hypothesis is constituted by the sum of the masses of all
Sets enclosed by it (i.e. the sum of the masses of all subsets of the hypothesis). It is the amount of belief that it will directly support to that of a given hypothesis at least in part, forming that of a lower bound.
Plausibility is 1 minus the sum of that of the masses of all sets whose intersection with the hypothesis is empty. It is an upper bound on the possibility that the hypothesis could possibly happen, up to that value, because there is only so much evidence that contradicts that hypothesis.
Example:
A proposition say that of the "the cat in the box is dead."
Suppose we have belief of 0.5 and plausibility of 0.8 for that of the proposition.
Example:
Suppose we have belief of 0.5 and plausibility of 0.8 for the proposition.
Evidence to state strongly, that the proposition is true with that of the confidence 0.5. Evidence contrary to hypothesis ("the cat is alive") has confidence 0.2.
Remaining mass of 0.3 (the gap between the 0.5 supporting evidence and the 0.2 contrary evidence) is "indeterminate," meaning that the
Cat could either be dead or alive. This interval represents the level of uncertainty based on the evidence in the system.
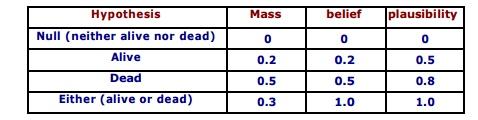
Null hypothesis is set to zero by that of the definition, corresponds to that of the "no solution". Orthogonal hypotheses "Alive" and "Dead" have probabilities of 0.2 and 0.5, respectively. This could correspond to that of the "Live/Dead Cat Detector"
Signals, which have respective reliabilities of 0.2 and 0.5. All-encompassing "Either" hypothesis (simply acknowledges there is a cat in the box) picks up the slack so that the sum of the masses is 1. Belief for the "Alive" and "Dead" hypotheses matches to that of their corresponding masses because they have no of the subsets;
Belief for "Either" consists of the sum of all of the three masses (Either, Alive, and Dead) because "Alive" and "Dead" are each subsets of that of the "Either".
"Alive" plausibility is 1- m (Death) and "Dead" plausibility is 1- m (Alive). "Either" plausibility sums m(Alive) + m(Dead) + m(Either).
Universal hypothesis ("Either") will always have that of the100% belief and plausibility; it acts as a checksum of the sorts.
Dempster-Shafer Calculus
In the previous slides, two specific examples of Belief and plausibility have been stated. It would now be easy to understand their generalization.
The Dempster-Shafer (DS) Theory requires that of a Universe of the Discourse U (or Frame of Judgment) consisting of that of the mutually exclusive alternatives, corresponding to an attribute of that of the value domain. For instance, in the satellite image of the classification the set U may consist of all of the possible classes of interest.
Each subset S ⊆ U is assigned a basic probability m(S), a belief Bel(S), and a plausibility Pls(S) so that m(S), Bel(S), Pls(S) ∈ [0, 1] and Pls(S) ≥ Bel(S) where
m represents the strength of an evidence, is the basic probability;
e.g., a group of pixels belong to that of the certain class, may be assigned value m.
Bel(S) summarizes all the reasons to believe S.
Pls(S) expresses how much one should believe in S if all currently unknown facts were to support S.
The true belief in S is somewhere in the belief interval [Bel(S), Pls(S)].
The basic probability assignment m is defined as function
m: 2U → [0,1], where m(Ø) = 0 and sum of m over all subsets of
U is 1 (i.e., ∑ S ⊆ U m(s) = 1).
For a given basic probability assignment m, the belief Bel of a subset A of U is the sum of m(B) for all subsets B of A , and the plausibility Pls of a subset A of U is Pls(A) = 1 - Bel(A') (5) where A' is complement of A in U.
Summarize:
The confidence interval is that interval of probabilities within which the true probability lies with that of a certain confidence that based on that of the belief "B" and the plausibility "PL" provided by some of the evidence "E" for that of a proposition "P". The belief brings together all the evidence that would lead us to believe in the proposition P with some certainty.
The plausibility brings together the evidence that is compatible with the proposition P and is not inconsistent with it.
If "Ω" is the set of possible outcomes, then a mass probability "M" is defined for each member of the set 2Ω and takes values in the range [0,1] . The Null set, "ф", is also a member of 2Ω.
Example
If Ω is the set { Flu (F), Cold (C), Pneumonia (P) }
Then 2Ω is the set Confidence interval is {ф, {F}, {C}, {P}, {F, C}, {F, P}, {C, P}, {F, C, P}} then defined as where
B(E) = ∑A M , where A ⊆ E i.e., all evidence that makes us believe in the correctness of P, and
PL(E) = 1 – B(¬E) = ∑¬A M , where ¬A ⊆ ¬E i.e., all the evidence that contradicts P.
Combining Beliefs
The Dempster-Shafer calculus combines that of the available evidences resulting in a belief and a plausibility in the combined evidence that represents a consensus on the correspondence. The model maximizes that of the belief in that of the combined evidences.
The rule of combination states that two basic probability assignments M1 and M2 are combined into a by third basic probability assignment the normalized orthogonal sum m1 (+) m2 stated below.
Suppose M1 and M2 are two of the belief functions.
Let X be the set of subsets of Ω to which M1 assigns a nonzero value and let Y be a similar set for M2 , then a new belief function M3 from the combination of beliefs in M1 and M2 is obtained as
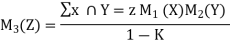
Where ∑ x ∩ Y = ф M1(X) M2(Y), for Z = ф
M3 (ф) is defined to be 0 so that the orthogonal sum remains that of a basic probability assignment.
Key takeaway
DST is a mathematical theory of evidence based on belief functions and plausible reasoning. It is used to combine that of the separate pieces of the information (evidence) to calculate that of the probability of an event.
References:
- Elaine Rich, Kevin Knight and Shivashankar B Nair, “Artificial Intelligence”, Mc Graw Hill Publication, 2009.
- Dan W. Patterson, “Introduction to Artificial Intelligence and Expert System”, Pearson Publication,2015.
- Saroj Kaushik, “Artificial Intelligence”, Cengage Learning, 2011.