Unit - 2
Linear Regression
One of the most basic and widely used Machine Learning methods is linear regression. It's a statistical technique for performing predictive analysis. Sales, salary, age, product price, and other continuous/real or numeric variables are predicted using linear regression.
The linear regression algorithm reveals a linear relationship between a dependent (y) variable and one or more independent (y) variables, thus the name. Because linear regression reveals a linear relationship, it determines how the value of the dependent variable changes as the value of the independent variable changes.
The link between the variables is represented by a slanted straight line in the linear regression model. Consider the following illustration:
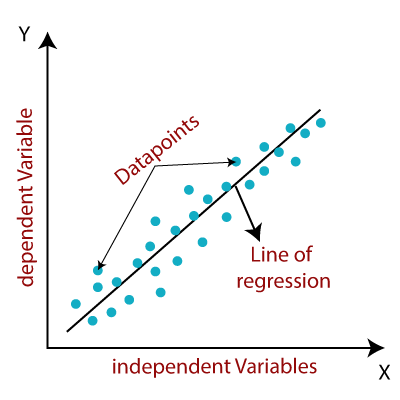
Fig 1: Linear regression model
A linear regression can be expressed mathematically as:
y= a0+a1x+ ε
Here,
Y= Dependent Variable (Target Variable)
X= Independent Variable (predictor Variable)
a0= intercept of the line (Gives an additional degree of freedom)
a1 = Linear regression coefficient (scale factor to each input value).
ε = random error
The values for the x and y variables are training datasets for the representation of a Linear Regression model.
Types of Linear Regression
Linear regression algorithms are further separated into two types:
● Simple Linear Regression - Simple Linear Regression is a Linear Regression approach that uses a single independent variable to predict the value of a numerical dependent variable.
● Multiple Linear Regression - Multiple Linear Regression is a Linear Regression approach that uses more than one independent variable to predict the value of a numerical dependent variable.
Gradient Descent is one of the most widely used optimization techniques for training machine learning models by minimising the difference between expected and actual results. In addition, Neural Networks are trained via gradient descent.
The task of minimizing/maximizing an objective function f(x) parameterized by x is referred to as an optimization algorithm in mathematics. Optimization is the task of minimising the cost function parameterized by the model's parameters in machine learning. The basic goal of gradient descent is to use iteration of parameter updates to minimise the convex function. These machine learning models can be utilised as strong tools for Artificial Intelligence and many computer science applications once they have been tuned.
Types of Gradient Descent
The Gradient Descent learning algorithm can be separated into Batch gradient descent, stochastic gradient descent, and mini-batch gradient descent based on the error in various training models. Let's look at the various types of gradient descent:
Batch Gradient Descent:
After analysing all training examples, batch gradient descent (BGD) is used to find the error for each point in the training set and update the model. The training period is the name given to this procedure. To put it another way, it's a greedy technique in which we have to add up all of the cases for each update.
Advantages
Batch gradient descent has the following advantages:
● In comparison to other gradient descent methods, it produces less noise.
● It ensures that gradient descent convergence is stable.
● Because all resources are employed for all training samples, it is computationally efficient.
Stochastic gradient descent
A variant of gradient descent called stochastic gradient descent (SGD) runs one training example every iteration. In other words, it processes a training epoch for each example in a dataset and changes the parameters of each training example one by one. It is easy to store in allocated memory because it only takes one training sample at a time. However, when compared to batch gradient systems, it exhibits some computational inefficiency due to the frequent updates that necessitate more detail and speed. It is also viewed as a noisy gradient due to the rapid changes. However, it can occasionally be useful in locating the global minimum as well as avoiding the local minimum.
Advantages
Learning occurs on every occurrence in stochastic gradient descent (SGD), and it has a few advantages over other gradient descent methods.
● It is simpler to allocate RAM in the required location.
● When compared to batch gradient descent, it is rather quick to compute.
● For huge datasets, it is more efficient.
Key takeaway
By calculating the gradient of the cost function, gradient descent is utilised to minimise the MSE.
Gradient descent is a technique for updating line coefficients by lowering the cost function in a regression model.
It is accomplished by selecting a random set of coefficient values and then iteratively updating the values to arrive at the lowest cost function.
Logistic Regression
Another approach to linear classification is the logistic regression model, which, despite its name, is a classification rather than a regression system.
In Logistic regression, we take a weighted linear combination of input features and pass it through a sigmoid function which outputs a number between 1 and 0. Unlike perceptron, which only tells us which side of the plane the point lies on, logistic regression gives a likelihood of a point lying on a particular side of the plane.
The probability of classification would be very similar to 1 or 0 as the point goes far away from the plane. The chance of classification of points very close to the plane is close to 0.5.
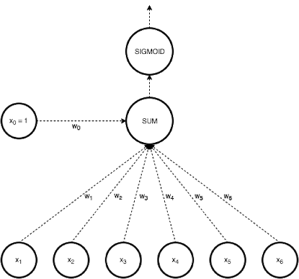
Fig 2: Logistic regression
The model is defined in terms of K-1 log-odds ratios, with an arbitrary class chosen as reference class (in this example it is the last class, K) (in this example it is the last class, K). Consequently, the difference between log-probabilities of belonging to a given class and to the reference class is modelled linearly as
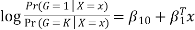
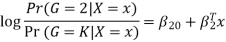
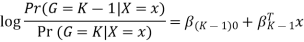
Where G stands for the real, observed class. From here, the probabilities of an observation belonging to each of the groups can be determined as
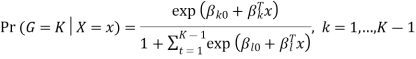
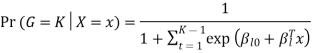
That clearly shows that all class probabilities add up to one.
Logistic regression models are usually calculated by maximum likelihood. Much as linear models for regression can be regularised to increase accuracy, so can logistic regression. In reality, L2 penalty is the default setting. It also supports L1 and Elastic Net penalties (to read more on these, check out the link above), but not all of them are supported by all solvers.
Overfitting
When a model learns the information and noise in the training data to the point where it degrades the model's performance on fresh data, this is known as overfitting. This means that the model picks up on noise or random fluctuations in the training data and learns them as ideas. The issue is that these notions do not apply to fresh data, limiting the models' ability to generalise.
Nonparametric and nonlinear models, which have more flexibility when learning a target function, are more prone to overfitting. As a result, many nonparametric machine learning algorithms incorporate parameters or strategies that limit and constrain the amount of detail learned by the model.
Decision trees, for example, are a nonparametric machine learning technique that is extremely versatile but susceptible to overfitting training data. This issue can be solved by pruning a tree after it has learned to remove part of the information it has gathered.
When our machine learning model tries to cover all of the data points in a dataset, or more than the required data points, overfitting occurs. As a result, the model begins to cache noise and erroneous values from the dataset, all of which reduces the model's efficiency and accuracy. Low bias and large variance characterise the overfitted model.
As we supply more training to our model, the odds of overfitting rise. It indicates that the more we train our model, the more likely it is to become overfitted.
In supervised learning, overfitting is the most common issue.
Regularization
One of the most fundamental topics in machine learning is regularisation. It's a method of preventing the model from overfitting by providing additional data.
When using training data, the machine learning model may perform well, but when using test data, it may not. It means that the model is unable to anticipate the outcome when dealing with unknown data by injecting noise into the output, and as a result, the model is said to as overfitted. A regularisation technique can be used to solve this problem.
This strategy can be applied in such a way that all variables or features in the model are preserved but the magnitude of the variables is reduced. As a result, the model's accuracy and generalisation are preserved.
Its main function is to minimise or regularise the coefficient of features to zero. "In regularisation technique, we minimise the magnitude of the features while preserving the same amount of features," to put it simply.
Techniques
The following are some of the most often used regularisation techniques:
● L1 regularization
● L2 regularization
● Dropout regularization
LASSO (Least Absolute Shrinkage and Selection Operator) regression is a regression model that employs the L1 Regularization approach.
Ridge regression is a regression model that use the L2 regularisation technique.
The "absolute value of magnitude" of the coefficient is added to the loss function as a penalty term in Lasso Regression (L).
Ridge regression
Ridge regression is one of the varieties of linear regression that introduces a little amount of bias to improve long-term predictions.
Ridge regression is a model regularisation technique that reduces the model's complexity. L2 regularisation is another name for it.
The cost function is changed in this method by including a penalty term. Ridge Regression penalty is the degree of bias introduced into the model. We may determine it by multiplying the squared weight of each individual feature by the lambda.
Lasso regression
Another regularisation technique for reducing model complexity is lasso regression. Least Absolute and Selection Operator is what it stands for.
It's similar to the Ridge Regression, but instead of a square of weights, the penalty term simply contains absolute weights.
Because it uses absolute data, it can reduce the slope to zero, whereas Ridge Regression can only go close.
L1 regularisation is another name for it.
Key takeaway
Regularization is a strategy for reducing mistakes and avoiding overfitting by fitting the function suitably on the supplied training set.
Support Vector Machine
SVM is another linear classification algorithm (One which separates data with a hyperplane) just like logistic regression and perceptron algorithms.
Given any linearly separable data, we can have multiple hyperplanes that can function as a separation boundary as shown. SVM selects the "optimal" hyperplane of all candidate hyperplanes.
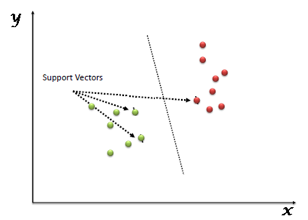
Fig 3: Support vector machine
To understand definition of "optimal" hyperplane, let us first define some concepts we will use
● Margin: It is the distance of the separating hyperplane to its nearest point/points.
● Support Vectors: The point/points closest to the dividing hyperplane.
The optimal hyperplane is defined as the one which maximises the margin. Thus SVM is posed as an optimization problem where we have to maximise margin subject to the constraint that all points lie on the correct side of the separating hyperplane
If all candidate hyperplanes correctly classify the data, why is maximum margin hyperplane the optimal one? One intuitive explanation is - If the incoming samples to be classified contain noise, we do not want them to cross the boundary and be classified incorrectly.
Advantages:
● It works very well with a clear margin of separation
● It is useful in high dimensional spaces.
● It is useful in situations where the number of dimensions is greater than the number of samples.
● It uses a subset of training points in the decision function (called support vectors), so it is also memory efficient.
Disadvantages:
● It doesn’t work well when we have a broad data set because the necessary training time is higher.
● It also doesn’t work very well, when the data set has more noise i.e. target classes are overlapping.
● SVM doesn’t explicitly have probability estimates, these are determined using a costly five-fold cross-validation.
Key takeaway
Logistic Regression models the probabilities of an observation belonging to each of the classes through linear functions.
It is usually considered safer and more stable than discriminant analysis methods, since it is relying on less assumptions.
It also turned out to be the most accurate for our example spam results.
Decision Tree is a Supervised learning technique that can be used for both classification and Regression problems, but mostly it is preferred for solving Classification problems. It is a tree-structured classifier, where internal nodes represent the features of a dataset, branches represent the decision rules and each leaf node represents the outcome.
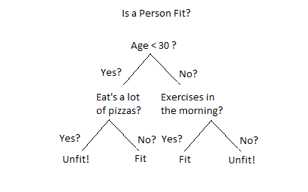
Fig 4: Decision tree example
In a Decision tree can be divided into:
● Decision Node
● Leaf Node
Decision nodes are marked by multiple branches that represent different decision conditions whereas output of those decisions is represented by leaf node and do not contain further branches.
The decision tests are performed on the basis of features of the given dataset.
It is a graphical representation for getting all the possible solutions to a problem/decision based on given conditions.
Decision Tree algorithm:
● Comes under the family of supervised learning algorithms.
● Unlike other supervised learning algorithms, decision tree algorithms can be used for solving regression and classification problems.
● Are used to create a training model that can be used to predict the class or value of the target variable by learning simple decision rules inferred from prior data (training data).
● Can be used for predicting a class label for a record we start from the root of the tree.
● Values of the root attribute are compared with the record’s attribute. On the basis of comparison, a branch corresponding to that value is considered and jumps to the next node.
Issues in Decision tree learning
● It is less appropriate for estimation tasks where the goal is to predict the value of a continuous attribute.
● This learning is prone to errors in classification problems with many classes and relatively small number of training examples.
● This learning can be computationally expensive to train. The process of growing a decision tree is computationally expensive. At each node, each candidate splitting field must be sorted before its best split can be found. In some algorithms, combinations of fields are used and a search must be made for optimal combining weights. Pruning algorithms can also be expensive since many candidate sub-trees must be formed and compared.
- Avoiding overfitting
A decision tree’s growth is specified in terms of the number of layers, or depth, it’s allowed to have. The data available to train the decision tree is split into training and testing data and then trees of various sizes are created with the help of the training data and tested on the test data. Cross-validation can also be used as part of this approach. Pruning the tree, on the other hand, involves testing the original tree against pruned versions of it. Leaf nodes are removed from the tree as long as the pruned tree performs better on the test data than the larger tree.
Two approaches to avoid overfitting in decision trees:
● Allow the tree to grow until it overfits and then prune it.
● Prevent the tree from growing too deep by stopping it before it perfectly classifies the training data.
2. Incorporating continuous valued attributes
3. Alternative measures for selecting attributes
● Prone to overfitting.
● Require some kind of measurement as to how well they are doing.
● Need to be careful with parameter tuning.
● Can create biased learned trees if some classes dominate.
Key takeaway
Decision Tree is a Supervised learning technique that can be used for both classification and Regression problems, but mostly it is preferred for solving Classification problems.
It is a tree-structured classifier, where internal nodes represent the features of a dataset, branches represent the decision rules and each leaf node represents the outcome.
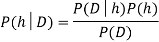
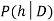=Posterior probability of h
P(h)= Prior probabilityy of h
P(D|h)=Probability of observing D given that h holds
P(D)= Probability of observing D
The posterior probability P(H|D) of a hypothesis is calculated as a product of the probability of the data given the hypothesis (P(D|H)), multiplied by the probability of the hypothesis (P(H)), divided by the probability of seeing the data, according to Bayes' Theorem. (P(D)) We've already seen one use of Bayes Theorem in class: in the analysis of Knowledge Cascades, we discovered that based on the conditional probabilities computed using Bayes' Theorem, reasonable decisions may be made where one's own personal information is omitted.
P(h/D) = P(D/h)P(h) / P(D)
By the law of product: P(h D) = P(h).P(D/h)
It's also commutative: P(D h) = P(D).P(h/D)
We can come up with the Bayesian formula as shown above if we combine them as equals. Also,
P(H) = Prior Probability.
P(D) = Likelihood of the data.
The Bayes' Theorem is the foundation of a form of Machine Learning known as Bayesian Machine Learning.
The Naive Bayes classifier is a tautological Bayesian Machine Learning technique that uses Bayes' Rule with the strong independence assumption that features in the dataset are conditionally independent of each other, given that we know the data class.
To comprehend Bayes Theorem in Machine Learning, it is necessary to comprehend that Bayes Theorem is quite useful in estimating value precision. Let's start at the beginning to understand how. The Bayes Theorem is a statement and theorem made by a British mathematician in the 18th century. He came up with a formula that works and is employed in conditional probability. What is conditional probability, exactly?
It's a phrase that refers to the likelihood of getting an answer to a question or predicting a likely outcome based on recent outcomes. A single statement is a method or process for cross-checking or updating existing forecasts in order to reduce the probability of making errors. In Machine Learning, this is how we express the Bayes Theorem.
Bayes' theorem is a mathematical formula for calculating the probability of an event based on ambiguous information. It is also known as Bayes' rule, Bayes' law, or Bayesian reasoning.
In probability theory, it relates the conditional and marginal probabilities of two random events.
The inspiration for Bayes' theorem came from British mathematician Thomas Bayes. Bayesian inference is a technique for applying Bayes' theorem, which is at the heart of Bayesian statistics.
It's a method for calculating the value of P(B|A) using P(A|B) knowledge.
Bayes' theorem can update the probability forecast of an occurrence based on new information from the real world.
Example: If cancer is linked to one's age, we can apply Bayes' theorem to more precisely forecast cancer risk based on age.
Bayes' theorem can be derived using the product rule and conditional probability of event A with known event B:
As a result of the product rule, we can write:
P(A ⋀ B)= P(A|B) P(B) or
In the same way, the likelihood of event B if event A is known is:
P(A ⋀ B)= P(B|A) P(A)
When we combine the right-hand sides of both equations, we get:
The above equation is known as Bayes' rule or Bayes' theorem (a). This equation is the starting point for most current AI systems for probabilistic inference.
It displays the simple relationship between joint and conditional probabilities. Here,
P(A|B) is the posterior, which we must compute, and it stands for Probability of hypothesis A when evidence B is present.
The likelihood is defined as P(B|A), in which the probability of evidence is computed after assuming that the hypothesis is valid.
Prior probability, or the likelihood of a hypothesis before taking into account the evidence, is denoted by P(A).
Marginal probability, or the likelihood of a single piece of evidence, is denoted by P(B).
In general, we can write P (B) = P(A)*P(B|Ai) in the equation (a), therefore the Bayes' rule can be expressed as:
Where A1, A2, A3,..... Is a set of mutually exclusive and exhaustive events, and An is a set of mutually exclusive and exhaustive events.
Use of Bayes’ Theorem
The purpose of doing an expert task, such as medical diagnosis, is to identify identifications (diseases) based on observations (symptoms). A relationship like this can be found in Bayes' Theorem.
P(A | B) = P(B | A) * P(A) / P(B)
Suppose: A=Patient has measles, B =has a rash
Then: P(measles/rash)=P(rash/measles) * P(measles) / P(rash)
Based on the known statistical values on the right, the desired diagnostic relationship on the left can be determined.
Applications of Bayes theorem
The theorem has a wide range of applications that aren't confined to finance. Bayes' theorem, for example, can be used to estimate the accuracy of medical test findings by taking into account how probable any specific person is to have a condition as well as the test's overall accuracy.
Key takeaway
Bayes' theorem, often known as Bayes' rule, Bayes' law, or Bayesian reasoning, is a mathematical formula for calculating the probability of an event based on ambiguous information.
The Bayesian inference is a method of applying Bayes' theorem, which is central to Bayesian statistics.
A boolean-valued function defined over a large quantity of training data can be regarded as a concept in Machine Learning. I discussed the principles of constructing a learning system in ML in my previous article, but we still need a learning mechanism or a suitable representation of the target concept to finish the design of a learning algorithm.
Finding the day when my friend Ramesh enjoys his favourite sport, for example, could be one viable target concept. We have some day attributes/features such as Sky, Air Temperature, Humidity, Wind, Water, and Forecast, and we have a target concept named EnjoySport based on these.
The following training example is accessible to you:
Eg | Sky | AirTemp | Humidity | Wind | Water | Forecast | EnjoySport |
1 | Sunny | Warm | Normal | Strong | Warm | Same | Yes |
2 | Sunny | Warm | High | Strong | Warm | Same | Yes |
3 | Rainy | Cold | High | Strong | Warm | Change | No |
4 | Sunny | Warm | High | Strong | Cool | Change | Yes |
Let's use TPE (Task, Performance, Experience) to formally design the problem:
Problem - Looking forward to the day when Ramesh likes his sport.
Task T - Learn to forecast the value of EnjoySport on any given day based on the values of the day's qualities.
Performance measure P - Total proportion of days properly predicted (EnjoySport).
Training experience E - A collection of days with labels (EnjoySport: Yes/No).
Take a look at a very basic hypothesis representation, which is made up of a set of restrictions in the instance attributes. With the help of example I we generate the following hypothesis h i for our training set:
Hi(x) := <x1, x2, x3, x4, x5, x6>
Where x1, x2, x3, x4, x5 and x6 are the values of Sky, AirTemp, Humidity, Wind, Water and Forecast.
Hence h1 will look like(the first row of the table above):
h1(x=1): <Sunny, Warm, Normal, Strong, Warm, Same > Note: x=1 represents a positive hypothesis / Positive example
We're looking for the most appropriate hypothesis to reflect the concept. Ramesh, for example, only participates in his favourite sport on cold, humid days (This seems independent of the values of the other attributes present in the training examples).
h(x=1) = <?, Cold, High, ?, ?, ?>
Here ? indicates that any value of the attribute is acceptable. Note: The most generic hypothesis will be < ?, ?, ?, ?, ?, ?> where every day is a positive example and the most specific hypothesis will be <?,?,?,?,?,? > where no day is a positive example.
We'll go over the two most common methods for coming up with a good hypothesis:
● Find-S Algorithm
● List-Then-Eliminate Algorithm
The Bayes Optimal Classifier is a probabilistic model that predicts the most possible outcome for a new scenario.
The Bayes Theorem, which provides a principled way of estimating a conditional probability, is used to explain it. It's also related to Maximum a Posteriori (MAP), a probabilistic method for determining the most likely hypothesis for a training dataset.
In practice, computing the Bayes Optimal Classifier is computationally costly, if not difficult, and instead, simplifications like the Gibbs algorithm and Naive Bayes can be used to estimate the result.
The Bayes optimal classifier is a probabilistic model that makes the most probable prediction for a new example, given the training dataset.
This model is often referred to as the Bayes optimal learner, the Bayes classifier, Bayes optimal decision boundary, or the Bayes optimal discriminant function.
Bayes Classifier: A probabilistic model that predicts the most possible outcome for new data.
Any model that uses this equation to classify examples is a Bayes optimal classifier, and no other methodology can outperform it on average.
A Bayes optimal classifier, or Bayes optimal learner, is a method that classifies new instances according to [the equation]. On average, no other classification system that uses the same hypothesis space and prior information as this method will outperform it.
It means that any other algorithm that works with the same data, hypotheses, and prior probabilities cannot outperform this method on average. As a consequence, the term "optimal classifier" was coined.
Despite the fact that the classifier allows the best predictions, it isn't flawless due to the ambiguity in the training data and the problem domain and hypothesis space's incomplete coverage. As a consequence, the model will make mistakes. Bayes errors are the name given to these types of errors.
The Bayes error rate is the lowest possible test error rate provided by the Bayes classifier. [...] The irreducible error rate is analogous to the Bayes error rate.
The Bayes error is the smallest possible error that can be made since the Bayes classifier is optimal.
The Bayes Error is the smallest possible error when making predictions.
Key takeaway
The Bayes Optimal Classifier is a probabilistic model that predicts the most possible outcome for a new scenario.
The Bayes optimal classifier is a probabilistic model that makes the most probable prediction for a new example, given the training dataset.
The Naïve Bayes algorithm is comprised of two words Naïve and Bayes, Which can be described as:
● Naïve: It is called Naïve because it assumes that the occurrence of a certain feature is independent of the occurrence of other features. Such as if the fruit is identified based on color, shape, and taste, then red, spherical, and sweet fruit is recognized as an apple. Hence each feature individually contributes to identifying that it is an apple without depending on each other.
● Bayes: It is called Bayes because it depends on the principle of Bayes’ Theorem.
Naïve Bayes Classifier Algorithm
Naïve Bayes algorithm is a supervised learning algorithm, which is based on the Bayes theorem and used for solving classification problems. It is mainly used in text classification that includes a high-dimensional training dataset.
Naïve Bayes Classifier is one of the simple and most effective Classification algorithms which help in building fast machine learning models that can make quick predictions.
It is a probabilistic classifier, which means it predicts based on the probability of an Object.
Some popular examples of the Naïve Bayes Algorithm are spam filtration, Sentimental analysis, and classifying articles.
Bayes’ Theorem:
● Bayes’ theorem is also known as Bayes’ Rule or Bayes’ law, which is used to determine the probability of a hypothesis with prior knowledge. It depends on the conditional probability.
● The formula for Bayes’ theorem is given as:
Where,
● P(A|B) is Posterior probability: Probability of hypothesis A on the observed event B.
● P(B|A) is Likelihood probability: Probability of the evidence given that the probability of a hypothesis is true.
● P(A) is Prior Probability: Probability of hypothesis before observing the evidence.
● P(B) is a Marginal Probability: Probability of Evidence.
Working of Naïve Bayes’ Classifier can be understood with the help of the below example:
Suppose we have a dataset of weather conditions and corresponding target variable “Play”. So using this dataset we need to decide whether we should play or not on a particular day according to the weather conditions. So to solve this problem, we need to follow the below steps:
Convert the given dataset into frequency tables.
Generate a Likelihood table by finding the probabilities of given features.
Now, use Bayes theorem to calculate the posterior probability.
Problem: If the weather is sunny, then the Player should play or not?
Solution: To solve this, first consider the below dataset:
Outlook Play
0 Rainy Yes
1 Sunny Yes
2 Overcast Yes
3 Overcast Yes
4 Sunny No
5 Rainy Yes
6 Sunny Yes
7 Overcast Yes
8 Rainy No
9 Sunny No
10 Sunny Yes
11 Rainy No
12 Overcast Yes
13 Overcast Yes
Frequency table for the Weather Conditions:
Weather Yes No
Overcast 5 0
Rainy 2 2
Sunny 3 2
Total 10 5
Likelihood table weather condition:
Weather No Yes
Overcast 0 5 5/14 = 0.35
Rainy 2 2 4/14 = 0.29
Sunny 2 3 5/14 = 0.35
All 4/14=0.29 10/14=0.71
Applying Bayes’ theorem:
P(Yes|Sunny)= P(Sunny|Yes)*P(Yes)/P(Sunny)
P(Sunny|Yes)= 3/10= 0.3
P(Sunny)= 0.35
P(Yes)=0.71
So P(Yes|Sunny) = 0.3*0.71/0.35= 0.60
P(No|Sunny)= P(Sunny|No)*P(No)/P(Sunny)
P(Sunny|NO)= 2/4=0.5
P(No)= 0.29
P(Sunny)= 0.35
So P(No|Sunny)= 0.5*0.29/0.35 = 0.41
So as we can see from the above calculation that P(Yes|Sunny)>P(No|Sunny)
Hence on a Sunny day, the Player can play the game.
Advantages of Naïve Bayes Classifier:
● Naïve Bayes is one of the fast and easy ML algorithms to predict a class of datasets.
● It can be used for Binary as well as Multi-class Classifications.
● It performs well in Multi-class predictions as compared to the other Algorithms.
● It is the most popular choice for text classification problems.
Disadvantages of Naïve Bayes Classifier:
● Naive Bayes assumes that all features are independent or unrelated, so it cannot learn the relationship between features.
Applications of Naïve Bayes Classifier:
● It is used for Credit Scoring.
● It is used in medical data classification.
● It can be used in real-time predictions because Naïve Bayes Classifier is an eager
● learner.
● It is used in Text classification such as Spam filtering and Sentiment analysis.
Types of Naïve Bayes Model:
There are three types of Naive Bayes Model, which are given below:
Gaussian: The Gaussian model assumes that features follow a normal distribution.
This means if predictors take continuous values instead of discrete, then the model assumes that these values are sampled from the Gaussian distribution.
Multinomial: The Multinomial Naïve Bayes classifier is used when the data is multinomial distributed. It is primarily used for document classification problems, it means a particular document belongs to which category such as Sports, Politics, education, etc.
The classifier uses the frequency of words for the predictors.
Bernoulli: The Bernoulli classifier works similarly to the Multinomial classifier, but the predictor variables are the independent Booleans variables. Such as if a particular word is present or not in a document. This model is also famous for document classification tasks.
Key takeaway
The Naïve Bayes algorithm is a supervised learning algorithm, which is based on the Bayes theorem and used for solving classification problems.
The Naïve Bayes Classifier is one of the simple and most effective Classification algorithms which help in building fast machine learning models that can make quick predictions.
Bayes’ theorem is also known as Bayes’ Rule or Bayes’ law, which is used to determine the probability of a hypothesis with prior knowledge
The Bayesian Belief Network (BBN) is an important framework technology for dealing with probabilistic occurrences in order to handle an issue with any level of uncertainty. Variables and their unique dependencies are visually presented in a directed graph with no directed cycles in a probabilistic graphical model (DAG).
The BBN displays conditional dependencies between two or more entirely arbitrary variables in layman's terms.
These networks are entirely probabilistic and are used to detect possible anomalies. As a result, they're ideal for use in machine learning, which primarily relies on anomaly detection.
The Bayesian belief network isn't new, and machine learning isn't the only application that makes use of it. As this network is utilised to, it has a wide range of applications and use cases.
● Predicting based on historical data;
● Detecting possible data anomalies;
● Diagnosing existing issues;
● Providing automatic insight;
● Logic and reasoning within AI;
● Binary decision making when exposed to unpredictability;
The Bayesian Belief Network is an important data science feature that is used in AI, Big Data, and Data Mining in addition to machine learning.
How is the Bayesian Belief Network Applied in Machine Learning?
Because machine learning is all about probability, the Bayesian Belief Network can be used to a wide range of applications. In machine learning, BBN's key purpose is to depict the probability model for each given domain, assess and explain probabilities for any given scenario using factual data and evidence, and supervise the link between the various random variables in any given condition.
These networks provide a visual probability model, which is represented by a graph with data nodes and oriented edges. Through this probability model, the BBN determines the correlations and dependencies between the given variables in any given sheet of data, enabling for machine learning process elucidation, calculations, and decision-making.
Each node defines its domain variable, and each node is specified by arcs. A conditional probability distribution table, which is a predefined collection of integrated random variables, quantifies all of the nodes in question.
The BBN models are the theorem's defining feature, and their construction determines the theorem's success rate. The better the data, the better the data derivatives, and the higher the BBN probability event estimation.
The Bayesian Belief Network is important in machine learning because it verifies nearly every step of the process, including data pre-processing, learning, and post-processing. The BBN is utilised in the unsupervised building of deep neural networks by structure learning, which is made possible by Bayes' theorem and the use of the generative graph. The algorithmic nature of this application lends itself to machine learning, and BBN plays an even bigger role in the machine learning process thanks to enhanced data organisation.
Key takeaway
The Bayesian Belief Network (BBN) is an important framework technology for dealing with probabilistic occurrences in order to handle an issue with any level of uncertainty.
In real-world machine learning applications, there are frequently numerous important features accessible for learning, but only a tiny fraction of them is observable. So, for variables that are sometimes observable and sometimes not, we may learn from the instances where the variable is visible and then predict its value in the cases where it is not.
On the other hand, the Expectation-Maximization algorithm can be used to predict the values of latent variables (variables that are not directly observable and are instead inferred from the values of other observed variables) if the general form of probability distribution governing those latent variables is known. Many unsupervised clustering techniques in the field of machine learning are based on this algorithm.
Arthur Dempster, Nan Laird, and Donald Rubin published a paper in 1977 that explained, proposed, and named it. When latent variables are involved and the data is missing or partial, it is utilised to find the local maximum likelihood parameters of a statistical model.
In statistical models, the EM approach can be used to find the local maximum likelihood estimates/parameters (MLE) or maximum a posteriori (MAP) estimates/parameters for latent variables (unobservable variables inferred from observable variables).
Or, to put it another way, the EM method in machine learning uses observable examples of latent variables to predict values in instances that are unobservable for learning, and it continues until the values converge.
The EM algorithm is an iterative approach that revolves between two modes: the first, named E-step, estimates missing or latent variables, and the second, termed M-step, optimises model parameters that better explain data. i.e.
E - step: Estimates the dataset's missing values.
M - step: While the data is still available, maximise the model parameters.
Given the generalised form of probability distribution that is related with these latent variables, the procedure is used to predict these values or to compute missing or incomplete data.
Working of EM Algorithm
Let's take a closer look at how this algorithm works.
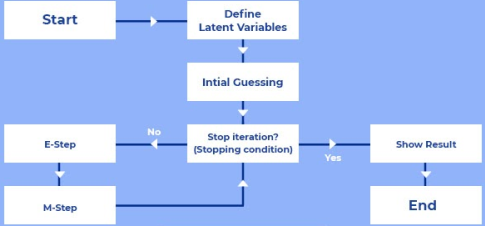
Fig 5: Workflow of EM algorithm
Step 1 - We suppose that observed data or initial values of the parameters are derived from the specified model, which has one set of missing or incomplete data and another set of starting parameters.
As a result, the system is given an entire set of partial observed data, presuming that the observed data comes from a specified model.
Step 2 - The values of unobservable instances, or missing data, are anticipated or approximated based on the observable value of the observable instances of the available data. Expectation step, or E-step, is the name given to this step.
The observed data is utilised to estimate or guess missing or partial data values that are used to update the variables in this stage.
Step 3 - We next update the settings and complete the data set using the E-step data. The M-step, or Maximization Step, is the name for this step. We also revise the hypothesis.
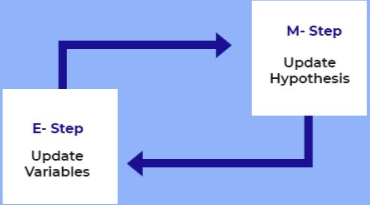
Fig 6: Working of E-step and M-step
We verify whether the values are converging or not as the final step, and if they are, we halt the procedure.
If the values do not converge, step 2 and step 3 will be repeated until the state of convergence is attained, otherwise we will simply repeat E-step and M-step.
Properties
The EM algorithm provides a number of useful qualities.
● It has numerical stability, and EM iteration improves the chances.
● It possesses reliable-universal convergence under underlying - favourable circumstances.
● It is quite simple to programme and search a little storage slot because it is implemented analytically and computationally. Simply said, it is easier to control convergence and programming eros by observing the continuous expansion in likelihood, which can be easily computed.
● Due to the low cost per iteration, the maximum number of iterations necessary for the EM algorithm can be counterbalanced as compared to other approaches.
● The answers to the M-steps are usually found in closed form.
● It can be globally accepted to obtain estimates of missing data.
Drawbacks
Aside from that, there are a few disadvantages to consider:
● Although it is unable to provide automated estimations of the covariance matrix of parameter estimates, this limitation can be overcome by using proper methods in conjunction with the EM algorithm.
● It can become quite slow at convergence and only reach local optima in some cases.
● Analytically, the E- and M-steps may be unmanageable in some circumstances.
● It necessitates the use of both forward and backward probability.
Key takeaway
The EM algorithm is an iterative approach that revolves between two modes: the first, named E-step, estimates missing or latent variables, and the second, termed M-step, optimises model parameters that better explain data.
References:
- Tom Mitchell. Machine Learning (McGraw Hill)
- Understanding Machine Learning. Shai Shalev-Shwartz and Shai Ben-David. Cambridge University Press.
- Christopher M. Bishop. Pattern Recognition and Machine Learning (Springer)
