Unit - 5
Probability & Statistics
Average or measures of Central tendency
An average is a value which is representative of a set of data. Average value may also be termed as measures of Central tendency. There are five types of averages in common.
(i) Arithmetic average or mean
(ii) Median
(iii) Mode
(iv) Geometric mean
(v) Harmonic mean
Arithmetic mean
If 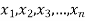 are n numbers then their arithmetic mean (A.M) is defined by
are n numbers then their arithmetic mean (A.M) is defined by

If the number 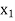 occurs
occurs 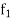 times
times 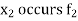 X and so on then
X and so on then
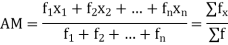
This is known as direct method.
Example 1. Find the mean of 20, 22, 25, 28, 30.
Solution. 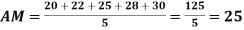
Example 2. Find the mean of the following:
Numbers | 8 | 10 | 15 | 20 |
Frequency | 5 | 8 | 8 | 4 |
Solution. 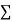 fx = 8×5 + 10×8 + 15×8 + 20×4 = 40+80+120+80=320
fx = 8×5 + 10×8 + 15×8 + 20×4 = 40+80+120+80=320
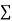 f = 5+8+8+4=25
f = 5+8+8+4=25
A.M.= 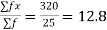
(b) Short cut method
Let a be the assumed mean, d the derivation of the variate x from a. Then
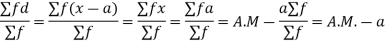
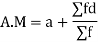
Example 3. Find the arithmetic mean for the following distribution
Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
Frequency | 7 | 8 | 20 | 10 | 5 |
Solution. Let assumed mean (a) = 25
Class | Mid-value (x) | Frequency (f) |  | Fd |
0-10 | 5 | 7 | -20 | -140 |
10-20 | 15 | 8 | -10 | -80 |
20-30 | 25 | 20 | 0 | 0 |
30-40 | 35 | 10 | + 10 | +100 |
40-50 | 45 | 5 | + 20 | +100 |
Total |
| 50 |
| -20 |
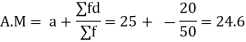
(C) Step diffusion method
Let a be the assumed mean, i the width of the class interval and
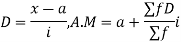
Example 4. Find the arithmetic mean of the data given in example 3 by step deviation method.
Solution. Let a =25
Class | Mid-value x | Frequency f | 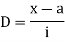 | f.D |
0-10 | 5 | 7 | -2 | -14 |
10-20 | 15 | 8 | -1 | -8 |
20-30 | 25 | 20 | 0 | 0 |
30-40 | 35 | 10 | +1 | +10 |
40-50 | 45 | 5 | +2 | +10 |
Total |
| 50 |
| -2 |
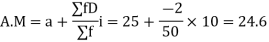
Median
Median is defined as the measure of the central atom when they are arranged in ascending or descending order of magnitude.
When the total number of the items is odd and equal to say n of  item gives the median.
item gives the median.
When the total number of The frequencies is even, say n, then there are two middle items and so the mean of the values of 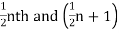 th items is the median.
th items is the median.
Example 5. Find the median of 6, 8, 9, 10, 11, 12, 13.
Solution. Total number of items =7
The middle item 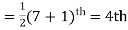
Median= value of the 4th item = 10
For grouped data, median 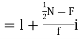
Where l is the lower limit of the median class, f is the frequency of the class, i is the width of the class interval, F is the total of all the the preceding frequencies of the median class and N is total frequency of the data.
Example 6. Find the value of median from the following data
Number of days for which absent (less than) | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
Number of students | 29 | 224 | 465 | 582 | 634 | 644 | 650 | 653 | 655 |
Solution. The given cumulative frequency distribution will first be converted into ordinary frequency as under:
Class interval | Cumulative frequency | Ordinary frequency |
0-5 | 29 | 29=29 |
5-10 | 224 | 224-29=105 |
10-15 | 465 | 465-224=241 |
15-20 | 582 | 582-465=117 |
20-25 | 634 | 634-582=52 |
25-30 | 644 | 644-634=10 |
30-35 | 650 | 650-644=6 |
35-40 | 653 | 653-650=3 |
40-45 | 655 | 655-653=2 |
Median = size of 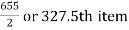
327.5th item lies in 10-15 which is the median class
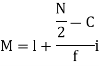
Where l stands for lower limit of median class.
N stands for the total frequency
C stands for cumulative frequency just preceding the median class
i stands for class interval
f stands for frequency for the median class
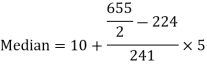
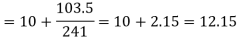
Mode
Mode is defined to be the size of the variable which occurs most frequently.
Example 7. Find the mode of the following items
0,1,6,7,2,3,7,6,6,2,6,0,5,6,0.
Solution. 6 occurs 5 times and no other item occurs 5 or more than 5 times, hence the mode is 6.
For grouped data, 
Where l is the lower limit of the modal class, f is the frequency of the modal class, i is the width of the class,  is the frequency before the model class and
is the frequency before the model class and 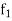 frequency of the modal class.
frequency of the modal class.
Empirical formula
Mean – Mode =3 [Mean – Median]
Example 8. Find the mode from the following data
Age | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 | 30-36 | 36-42 |
Frequency | 6 | 11 | 25 | 35 | 18 | 12 | 6 |
Solution.
Age | Frequency | Cumulative frequency |
0-6 | 6 | 6 |
6-12 | 11 | 17 |
12-18 | 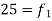 | 42 |
18-24 | 35 = f | 77 |
24-30 |  | 95 |
30-36 | 12 | 107 |
36-42 | 6 | 113 |
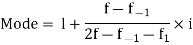
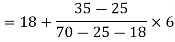
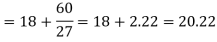
Geometric mean
If 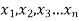 be n values of variates x, then the geometric mean
be n values of variates x, then the geometric mean

Example 10. Calculate the harmonic mean of 4,8,16.
Solution. 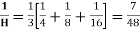

Average deviation on mean deviation
It is the mean of the absolute values of the definitions of given set of numbers from their arithmetic mean.
If 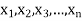 be a set of numbers with frequencies
be a set of numbers with frequencies 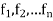 respectively. Let x be the arithmetic mean of the numbers
respectively. Let x be the arithmetic mean of the numbers 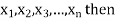
Mean deviation = 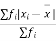
Example 11. Find the mean deviation of the following frequency distribution
Class | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 |
Frequency | 8 | 10 | 12 | 9 | 5 |
Solution. Let a = 15
Class | Mid-value x | Frequency f | d = x-a | Fd | |x-14| | f|x-14| |
0-6 | 3 | 8 | -12 | -96 | 11 | 88 |
6-12 | 9 | 10 | -6 | -60 | 5 | 50 |
12-18 | 15 | 12 | 0 | 0 | 1 | 12 |
18-24 | 21 | 9 | +6 | 54 | 7 | 63 |
24-30 | 27 | 5 | +12 | 60 | 13 | 65 |
Total |
| 44 |
| -42 |
| 278 |
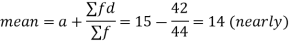
Average deviation= 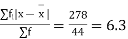
MOMENTS
The rth moment of a variable x about the mean x is usually denoted by is given by
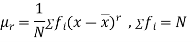
The rth moment of a variable x about any point a is defined by
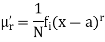
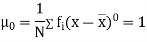
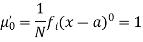
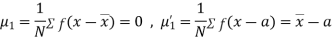
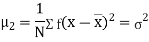
Relation between moments about mean and moment about any point:
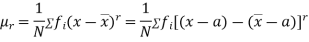
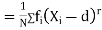 where
where and
and 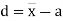
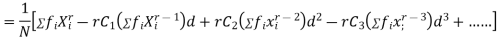

In particular
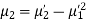

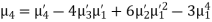
Note. 1. The sum of the coefficients of the various terms on the right‐hand side is zero.
2. The dimension of each term on right‐hand side is the same as that of terms on the left.
MOMENT GENERATING FUNCTION
The moment generating function of the variate 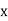 about
about 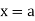 is defined as the expected value of
is defined as the expected value of 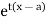 and is denoted
and is denoted 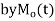 .
.

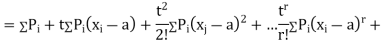
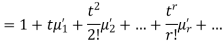
Where 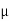 , ‘ is the moment of order
, ‘ is the moment of order 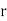 about
about 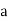
Hence 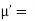 coefficient of
coefficient of  or
or 
Again 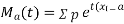 )
) 
Thus the moment generating function about the point  moment generating function about the origin.
moment generating function about the origin.
SKEWNESS:
Skewness denotes the opposite of symmetry. It is lack of symmetry. In a symmetrical series, the mode, the median, and the arithmetic average are identical.
Coefficient of skewness 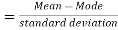
KURTOSIS: It measures the degree of peakedness of a distribution and is given by Measure of kurtosis.

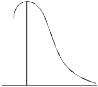
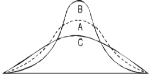
Negative skewness Positive skewness A: Mesokurtic B: Leptokurtic
C: Playkurtic
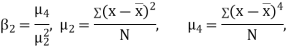
If 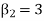 , the curve is normal or mesokurtic.
, the curve is normal or mesokurtic.
If 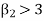 , the curve is peaked or leptokurtic.
, the curve is peaked or leptokurtic.
If 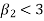 , the curve is flat topped or platykurtic
, the curve is flat topped or platykurtic
Example. The first four moments about the working mean 28.5 of distribution are 0.2 94, 7.1 44, 42.409 and 454.98. Calculate the moments about the mean. Also evaluate 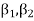 and comment upon the skewness and kurtosis of the distribution.
and comment upon the skewness and kurtosis of the distribution.
Solution. The first four moments about the arbitrary origin 28.5 are 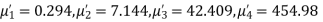
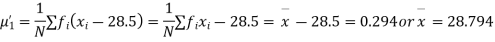
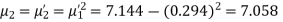
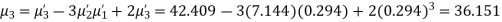
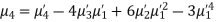
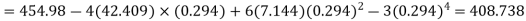
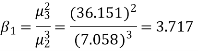
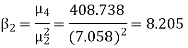
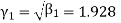 , which indicates considerable skewness of the distribution.
, which indicates considerable skewness of the distribution.
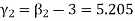 , which shows that the distribution is leptokurtic.
, which shows that the distribution is leptokurtic.
Example. Calculate the median, quartiles and the quartile coefficient of skewness from the following data:
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140=150 |
No. Of persons | 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
Solution. Here total frequency 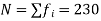
The cumulative frequency table is
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140=150 |
Frequency | 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
Cumulative Frequency | 12 | 30 | 65 | 107 | 157 | 202 | 222 | 230 |
Now, N/2 =230/2= 115th item which lies in 110 – 120 group.
Median or 
Also, 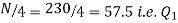 is 57.5th or 58th item which lies in 90-100 group.
is 57.5th or 58th item which lies in 90-100 group.
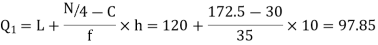
Similarly 3N/4 = 172.5 i.e. 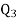 is 173rd item which lies in 120-130 group.
is 173rd item which lies in 120-130 group.

Hence quartile coefficient of skewness = 
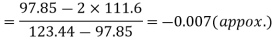
Correlation
So far we have confined our attention to the analysis of observations on a single variable. There are however, many phenomenon where the changes in one variable are related to the changes in the other variable. For instance the yield of a crop varies with the amount of rainfall, the price of a commodity increases with the reduction in its supply and so on. Such a data connecting two variables is called bivariate population.
To obtain a measure of relationship between the two variables, we plot their corresponding values on the graph taking one of the variable along the x axis and the other along the y axis. (Figure 25.6).
Let the origin be shifted to 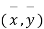 , where
, where 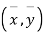 re the means of X’s and y's that the new coordinates are given by
re the means of X’s and y's that the new coordinates are given by
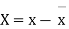
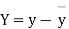
Now the points (X,Y) are so distributed over the four quadrants of XY plane that the product XY is positive in the first and third quadrant but negative in the second and fourth quadrants. The algebraic sum of the products can be taken as describing the trend of the dots in all the quadrants.
(i) If 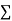 XY is positive, the trend of the dots is through the first and third quadrants.
XY is positive, the trend of the dots is through the first and third quadrants.
(ii) If 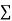 XY is negative the trend of two dots is in the second and fourth quadrants and
XY is negative the trend of two dots is in the second and fourth quadrants and
(iii) If 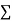 XY is zero, the points indicate no trend i.e. the points are evenly distributed over the quadrants.
XY is zero, the points indicate no trend i.e. the points are evenly distributed over the quadrants.
The 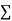 XY or better still
XY or better still 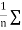 XY i.e. the average of n products may be taken as a measure of correlation. If we put X and Y in their units, i.e.
XY i.e. the average of n products may be taken as a measure of correlation. If we put X and Y in their units, i.e. 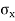 taking , as the unit for x and
taking , as the unit for x and 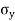 for y, then
for y, then
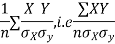
Is the measure of correlation.
Coefficient of correlation
The numerical measure of correlation is called the coefficient of correlation and is defined by the relation
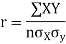
Where, X = deviation from the mean =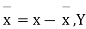 = devaluation from the mean
= devaluation from the mean 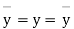
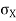 = Standard deviation of x series,
= Standard deviation of x series,  = standard deviation of y series and n = number of the values of the two variables
= standard deviation of y series and n = number of the values of the two variables
Methods of calculation
(a) Direct method. Substituting the value of 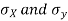 in the above formula we get
in the above formula we get

Another form of the formula (1) which is quite handy for calculation is
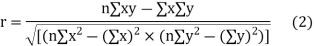
(b) Step deviation method. The direct method becomes very lengthy and tedious if the means of the two series are not integers. In such cases, use is made of assumed means. If 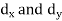 are step deviations from the assumed means, then
are step deviations from the assumed means, then
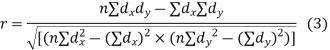
(c) Coefficient of correlation for grouped data. When x and y series are both given as frequency distributions these can be represented by a two way table known as the correlation table. The coefficient of correlation for such a bivariate frequency distribution is calculated by the formula

Where 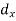 = derivation of the central values from the assumed mean of x series
= derivation of the central values from the assumed mean of x series
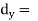 derivation of the central values from the assumed mean of y series
derivation of the central values from the assumed mean of y series
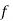 is the frequency corresponding to the pair (x, y)
is the frequency corresponding to the pair (x, y)
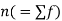 is the total number of frequency
is the total number of frequency
Example. Psychological test of the intelligence and of Engineering ability were applied to 10 students. Here is a record of ungrouped data showing intelligence ratio (I.R) and Engineering ratio (E.R). Calculate the coefficient of correlation.
Student | A | B | C | D | E | F | G | H | I | J |
I.R. | 105 | 104 | 102 | 101 | 100 | 99 | 98 | 96 | 93 | 92 |
E.R. | 101 | 103 | 100 | 98 | 95 | 96 | 104 | 92 | 97 | 94 |
Solution. We construct the following table
Student | Intelligence ratio x  | Engineering ratio y y 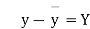 | 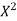 | 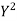 | XY |
A | 105 6 | 101 3 | 36 | 9 | 18 |
B | 104 5 | 103 5 | 25 | 25 | 25 |
C | 102 3 | 100 2 | 9 | 4 | 6 |
D | 101 2 | 98 0 | 4 | 0 | 0 |
E | 100 1 | 95 -3 | 1 | 9 | -3 |
F | 99 0 | 96 - 2 | 0 | 4 | 0 |
G | 98 -1 | 104 6 | 1 | 36 | -6 |
H | 96 -3 | 92 -6 | 9 | 36 | 18 |
I | 93 -6 | 97 -1 | 36 | 1 | 6 |
J | 92 -7 | 94 -4 | 49 | 16 | 28 |
Total | 990 0 | 980 0 | 170 | 140 | 92 |
From this table, mean of x, i.e. 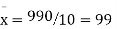 and mean of y, i.e.
and mean of y, i.e. 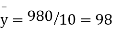
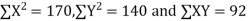
Substituting these value in the formula (1)p.744 we have
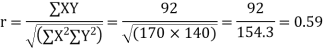
Example. The correlation table given below shows that the ages of husband and wife of 53 married couples living together on the census night of 1991. Calculate the coefficient of correlation between the age of the husband and that of the wife.
Age of husband | Age of wife | Total | ||||||
15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 | |||
15-25 | 1 | 1 | - | - | - | - | 2 | |
25-35 | 2 | 12 | 1 | - | - | - | 15 | |
35-45 | - | 4 | 10 | 1 | - | - | 15 | |
45-55 | - | - | 3 | 6 | 1 | - | 10 | |
55-65 | - | - | - | 2 | 4 | 2 | 8 | |
65-75 | - | - | - | - | 1 | 2 | 3 | |
Total | 3 | 17 | 14 | 9 | 6 | 4 | 53 | |
Solution.
Age of husband | Age of wife x series | Suppose 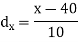 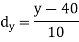 | |||||||||||
15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 |
Total f | |||||||
Years | Midpoint x | 20 | 30 | 40 | 50 | 60 | 70 | ||||||
Age group | Midpoint y |
|
| -20 | -10 | 0 | 10 | 20 | 30 | 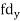 | 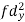 | 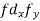 | |
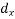  | -2 | -1 | 0 | 1 | 2 | 3 | |||||||
15-25 | 20 | -20 | -2 | 4 1 | 2 1 |
|
|
|
| 2 | -4 | 8 | 6 |
25-35 | 30 | -10 | -1 | 4 2 | 12 12 | 0 1 |
|
|
| 15 | -15 | 15 | 16 |
35-45 | 40 | 0 | 0 |
| 0 4 | 0 10 | 0 1 |
|
| 15 | 0 | 0 | 0 |
45-55 | 50 |
|
|
|
| 0 3 | 6 6 | 2 1 |
| 10 | 10 | 10 | 8 |
55-65 | 60 |
|
|
|
|
| 4 2 | 16 4 | 12 2 | 8 | 16 | 32 | 32 |
65-75 | 70 |
|
|
|
|
|
| 6 1 | 18 2 | 3 | 9 | 27 | 24 |
Total f | 3 | 17 | 14 | 9 | 6 | 4 | 53 = n | 16 | 92 | 86 | |||
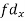 | -6 | -17 | 0 | 9 | 12 | 12 | 10 | Thick figures in small sqs. For 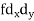 Check: 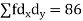 From both sides | |||||
 | 12 | 17 | 0 | 9 | 24 | 36 | 98 | ||||||
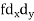 | 8 | 14 | 0 | 10 | 24 | 30 | 86 | ||||||
With the help of the above correlation table, we have
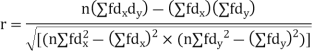
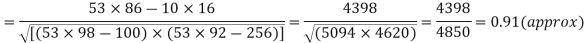
Lines of Regression
It frequently happens that the dots of the scatter diagram generally tends to cluster along a well- defined direction which suggests a linear relationship between the variables x and y. Such a line of best fit for the given distribution of dots is called the line of regression (figure 25.6). In fact there are two such lines, one giving the best possible mean values of y for each specified value pf x and the other giving the best possible mean values of x for given value of y. The former is known as the line of regression of y on x and the latter as the line of regression of x on y.
Consider first the line of regression of y on x. Let the straight line satisfying the general trend of n dots in a scatter diagram be
 (1)
(1)
We have to determine the constant a and b so that (1) gives for each value of x, the best estimate for the average value of y in accordance with the principle of least squares therefore, the normal equation for a and b are
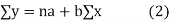
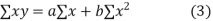
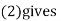
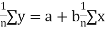 i.e.
i.e. 
This shows that 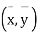 i.e. the mean of x and y lie on (1).
i.e. the mean of x and y lie on (1).
Shifting the origin to 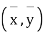 (3) takes the form of
(3) takes the form of

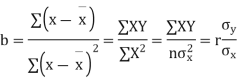
Cor. The correlation coefficient r is the geometric mean between the two regression coefficients
For 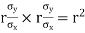
Example. The two regression equations of the variable x and y are x = 19.13 and y = 11.64 – 0.50 x. Find (i) mean of x’s (ii) mean of y’s and (iii) the correlation coefficient between x and y.
Solution. Since the mean of x’s and the mean of y’s lie on the two regression lines, we have
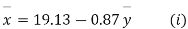
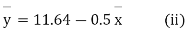
Multiplying (ii) by 0.87 and subtracting from (i) we have
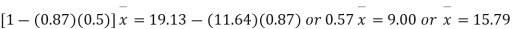
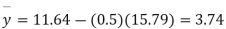
Regression coefficient of y and x is -0.50 and that of x and y is -0.87.
Now since the coefficient of correlation is the geometric mean between the two regression coefficients.
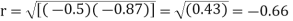
[-ve sign is taken since both the regression coefficients are –ve]
Example. If 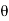 is the angle between the two regression lines show that
is the angle between the two regression lines show that
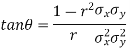
Explain the significance when 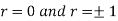 .
.
Solution. The equations to the line of regression of y on x and x on y are
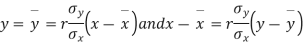
Their slopes are 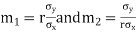
Thus, 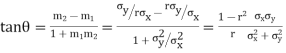
When r = 0,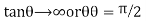 i.e. when the variable are independent, the two lines of regression are perpendicular to each other.
i.e. when the variable are independent, the two lines of regression are perpendicular to each other.
When  . Thus the line of regression coincide i.e. there is perfect correlation between the two variables.
. Thus the line of regression coincide i.e. there is perfect correlation between the two variables.
Example. While calculating correlation coefficient between two variables x and y from 25 pairs of observations, the following results were obtained : n = 25, 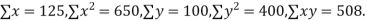 Later it was discovered at the time of checking that the pairs of values x -8,6 and y = 12, 8 were copied down as x = 6,8 and y = 14,6. Obtain the correct value of correlation coefficients.
Later it was discovered at the time of checking that the pairs of values x -8,6 and y = 12, 8 were copied down as x = 6,8 and y = 14,6. Obtain the correct value of correlation coefficients.
Solution. To get the correct results, we subtract the incorrect values and add the corresponding correct values.
The correct results would be
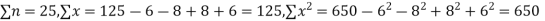
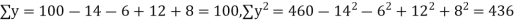

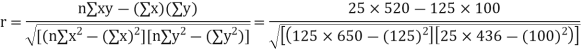
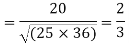
RANK CORRELATION
A group of n individuals may be arranged in order to merit with respect to some characteristics. The same group would give different orders for different characteristics. Considering the orders corresponding to two characteristics A and B, the correction between these n pairs of rank is called the rank correlation in the characteristics A and B for that group of individuals.
Let 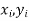 be the ranks of the ith individuals in A and B respectively. Assuming that no two individuals are bracketed equal in either case, each of the variables taking the values 1,2,3,…,n we have
be the ranks of the ith individuals in A and B respectively. Assuming that no two individuals are bracketed equal in either case, each of the variables taking the values 1,2,3,…,n we have
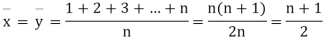
If X, Y be the deviations of x, y from their means, then

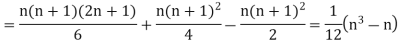
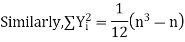
Now let, 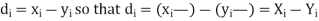
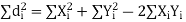

Hence the correlation coefficient between these variables is

This is called the rank correlation coefficient and is denoted by 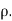
Example. Ten participants in a contest are ranked by two judges as follows:
x | 1 | 6 | 5 | 10 | 3 | 2 | 4 | 9 | 7 | 8 |
y | 6 | 4 | 9 | 8 | 1 | 2 | 3 | 10 | 5 | 7 |
Calculate the rank correlation coefficient 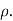
Solution. If 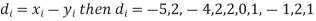
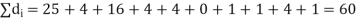
Hence, 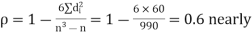
Example. Three judges A,B,C give the following ranks. Find which pair of judges has common approach
A | 1 | 6 | 5 | 10 | 3 | 2 | 4 | 9 | 7 | 8 |
B | 3 | 5 | 8 | 4 | 7 | 10 | 2 | 1 | 6 | 9 |
C | 6 | 4 | 9 | 8 | 1 | 2 | 3 | 10 | 5 | 7 |
Solution. Here n = 10
A (=x) | Ranks by B(=y) | C (=z) | 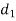 x-y | 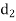 y - z | 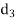 z-x | 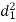
| 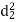 |  |
1 | 3 | 6 | -2 | -3 | 5 | 4 | 9 | 25 |
6 | 5 | 4 | 1 | 1 | -2 | 1 | 1 | 4 |
5 | 8 | 9 | -3 | -1 | 4 | 9 | 1 | 16 |
10 | 4 | 8 | 6 | -4 | -2 | 36 | 16 | 4 |
3 | 7 | 1 | -4 | 6 | -2 | 16 | 36 | 4 |
2 | 10 | 2 | -8 | 8 | 0 | 64 | 64 | 0 |
4 | 2 | 3 | 2 | -1 | -1 | 4 | 1 | 1 |
9 | 1 | 10 | 8 | -9 | 1 | 64 | 81 | 1 |
7 | 6 | 5 | 1 | 1 | -2 | 1 | 1 | 4 |
8 | 9 | 7 | -1 | 2 | -1 | 1 | 4 | 1 |
Total |
|
| 0 | 0 | 0 | 200 | 214 | 60 |
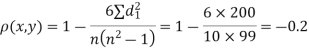
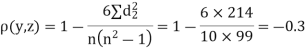
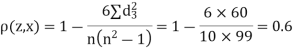
Since 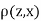 is maximum, the pair of judge A and C have the nearest common approach.
is maximum, the pair of judge A and C have the nearest common approach.
Hypothesis-
A hypothesis is a statement or a claim or an assumption about the value of a population parameter (e.g., mean, median, variance, proportion, etc.).
Similarly, in the case of two or more populations, a hypothesis is a comparative statement or a claim, or an assumption about the values of population parameters. (e.g., means of two populations are equal, the variance of one population is greater than other, etc.).
For example-
If a customer of a car wants to test whether the claim of the car of a certain brand gives the average of 30km/hr is true or false.
Simple, and composite hypotheses-
If a hypothesis specifies only one value or exact value of the population parameter then it is known as a simple hypothesis., and if a hypothesis specifies not just one value but a range of values that the population parameter may assume is called a composite hypothesis.
The null, and alternative hypothesis
The hypothesis is to be tested as called the null hypothesis.
The hypothesis which complements the null hypothesis is called the alternative hypothesis.
In the example of a car, the claim is 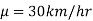 , and its complement is
, and its complement is 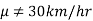 .
.
The null and alternative hypothesis can be formulated as-
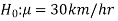
And
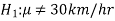
Testing a Hypothesis
Critical region-
Let 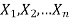 be a random sample drawn from a population having unknown population parameter
be a random sample drawn from a population having unknown population parameter 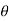 .
.
The collection of all possible values of 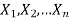 is called sample space, and a particular value represents a point in that space.
is called sample space, and a particular value represents a point in that space.
To test a hypothesis, the entire sample space is partitioned into two disjoint sub-spaces, say, 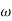 , and S –
, and S – 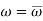 . If the calculated value of the test statistic lies in, then we reject the null hypothesis, and if it lies in
. If the calculated value of the test statistic lies in, then we reject the null hypothesis, and if it lies in 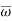 then we do not reject the null hypothesis. The region is called a “rejection region or critical region”, and the region
then we do not reject the null hypothesis. The region is called a “rejection region or critical region”, and the region 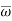 is called a “non-rejection region”.
is called a “non-rejection region”.
Therefore, we can say that
“A region in the sample space in which if the calculated value of the test statistic lies, we reject the null hypothesis then it is called a critical region or rejection region.”
The region of rejection is called the critical region.
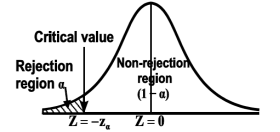
The critical region lies in one or two tails on the probability curve of the sampling distribution of the test statistic it depends on the alternative hypothesis.
Therefore, there are three cases-
CASE-1: if the alternative hypothesis is right-sided such as 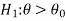 then the entire critical region of size
then the entire critical region of size 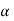 lies on the right tail of the probability curve.
lies on the right tail of the probability curve.
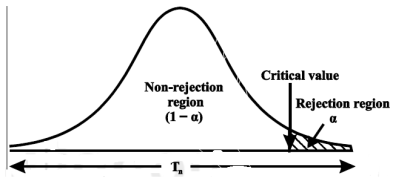
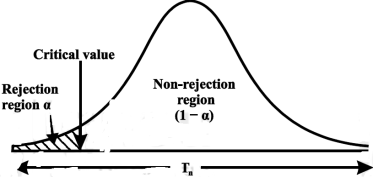
CASE-2: if the alternative hypothesis is left-sided such as 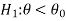 then the entire critical region of size
then the entire critical region of size 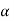 lies on the left tail of the probability curve.
lies on the left tail of the probability curve.
CASE-3: if the alternative hypothesis is two-sided such as 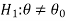 then the entire critical region of size
then the entire critical region of size 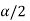 lies on both tail of the probability curve
lies on both tail of the probability curve
Type-1, and Type-2 error-
Type-1 error-
The decision relating to the rejection of null hypo. When it is true is called a type-1 error.
The probability of type-1 error is called the size of the test, it is denoted by 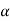 , and defined as-
, and defined as-

Note-
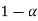 is the probability of a correct decision.
is the probability of a correct decision.
Type-2 error-
The decision relating to the non-rejection of null hypo. When it is false is called a type-1 error.
It is denoted by 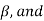 defined as-
defined as-
Decision |
 |  |
Reject 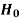 | Type-1 error | Correct decision |
Do not reject  | Correct decision | Type-2 error |
One-tailed, and two-tailed tests-
A test of testing the null hypothesis is said to be a two-tailed test if the alternative hypothesis is two-tailed whereas if the alternative hypothesis is one-tailed then a test of testing the null hypothesis is said to be a one-tailed test.
For example, if our null and alternative hypothesis are-
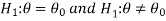
Then the test for testing the null hypothesis is two-tailed because the
An alternative hypothesis is two-tailed.
If the null and alternative hypotheses are-
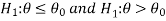
Then the test for testing the null hypothesis is right-tailed because the alternative hypothesis is right-tailed.
Similarly, if the null and alternative hypotheses are-
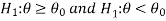
Then the test for testing the null hypothesis is left-tailed because the alternative hypothesis is left-tailed
Procedure for testing a hypothesis-
Step-1: first we set up the null hypothesis 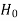 , and alternative hypothesis
, and alternative hypothesis 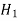 .
.
Step-2: After setting the null, and alternative hypothesis, we establish
Criteria for rejection or non-rejection of the null hypothesis, that is,
Decide the level of significance (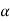 ), at which we want to test our
), at which we want to test our
Hypothesis. Generally, it is taken as 5% or 1% (α = 0.05 or 0.01).
Step-3: The third step is to choose an appropriate test statistic under H0 for
Testing the null hypothesis as given below
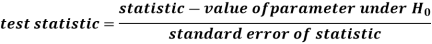
Now after doing this, specify the sampling distribution of the test statistic preferably in the standard form like Z (standard normal),  , t, F or any other well-known in the literature
, t, F or any other well-known in the literature
Step-4: Calculate the value of the test statistic described in Step III based on observed sample observations.
Step-5: Obtain the critical (or cut-off) value(s) in the sampling distribution of the test statistic, and construct rejection (critical) region of size  .
.
Generally, critical values for various levels of significance are put in the form of a table for various standard sampling distributions of test statistic such as Z-table, 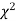 -table, t-table, etc
-table, t-table, etc
Step-6: After that, compare the calculated value of the test statistic obtained from Step IV, with the critical value(s) obtained in Step V, and locates the position of the calculated test statistic, that is, it lies in the rejection region or non-rejection region.
Step-7: in testing the hypothesis we have to conclude, it is performed as below-
First- If the calculated value of the test statistic lies in the rejection region at  level of significance then we reject the null hypothesis. It means that the sample data provide us sufficient evidence against the null hypothesis, and there is a significant difference between the hypothesized value and the observed value of the parameter
level of significance then we reject the null hypothesis. It means that the sample data provide us sufficient evidence against the null hypothesis, and there is a significant difference between the hypothesized value and the observed value of the parameter
Second- If the calculated value of the test statistic lies in the non-rejection region at 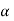 level of significance then we do not reject the null hypothesis. Its means that the sample data fails to provide us sufficient evidence against the null hypothesis, and the difference between hypothesized value, an observed value of the parameter due to fluctuation of sample
level of significance then we do not reject the null hypothesis. Its means that the sample data fails to provide us sufficient evidence against the null hypothesis, and the difference between hypothesized value, an observed value of the parameter due to fluctuation of sample
The procedure of testing of hypothesis for large samples-
A sample size of more than 30 is considered a large sample size. So that for large samples, we follow the following procedure to test the hypothesis.
Step-1: first we set up the null and alternative hypothesis.
Step-2: After setting the null, and alternative hypotheses, we have to choose the level of significance. Generally, it is taken as 5% or 1% (α = 0.05 or 0.01)., and accordingly rejection and non-rejection regions will be decided.
Step-3: The third step is to determine an appropriate test statistic, say, Z in the case of large samples. Suppose Tn is the sample statistic such as sample
Mean, sample proportion, sample variance, etc. for the parameter 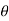
Then for testing the null hypothesis, the test statistic is given by
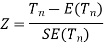
Step-4: the test statistic Z will assumed to be approximately normally distributed with mean 0, and variance 1 as
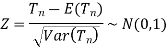
By putting the values in the above formula, we calculate test statistic Z.
Suppose z be the calculated value of Z statistic
Step-5: After that, we obtain the critical (cut-off or tabulated) value(s) in the sampling distribution of the test statistic Z corresponding to 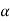 assumed in Step II. We construct the rejection (critical) region of size α in the probability curve of the sampling distribution of test statistic Z.
assumed in Step II. We construct the rejection (critical) region of size α in the probability curve of the sampling distribution of test statistic Z.
Step-6: Decide on the null hypothesis based on the calculated, and critical values of test statistic obtained in Step IV, and Step V.
Since critical value depends upon the nature of the test that it is a one-tailed test or two-tailed test so following cases arise-
Case-1 one-tailed test- when  (right-tailed test)
(right-tailed test)
In this case, the rejection (critical) region falls under the right tail of the probability curve of the sampling distribution of test statistic Z.
Suppose 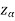 is the critical value at
is the critical value at  level of significance so the entire region greater than or equal to
level of significance so the entire region greater than or equal to 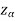 is the rejection region, and less than
is the rejection region, and less than
 is the non-rejection region
is the non-rejection region
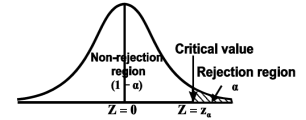
If z (calculated value ) ≥ 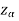 (tabulated value), that means the calculated value of test statistic Z lies in the rejection region, then we reject the null hypothesis H0 at
(tabulated value), that means the calculated value of test statistic Z lies in the rejection region, then we reject the null hypothesis H0 at 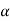 level of significance. Therefore, we conclude that sample data provides us sufficient evidence against the null hypothesis, and there is a significant difference between the hypothesized or specified value, and the observed value of the parameter.
level of significance. Therefore, we conclude that sample data provides us sufficient evidence against the null hypothesis, and there is a significant difference between the hypothesized or specified value, and the observed value of the parameter.
If z <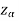 that means the calculated value of test statistic Z lies in the non-rejection region, then we do not reject the null hypothesis H0 at
that means the calculated value of test statistic Z lies in the non-rejection region, then we do not reject the null hypothesis H0 at 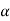 level of significance. Therefore, we conclude that the sample data fails to provide us sufficient evidence against the null hypothesis, and the difference between hypothesized value, an observed value of the parameter due to fluctuation of the sample.
level of significance. Therefore, we conclude that the sample data fails to provide us sufficient evidence against the null hypothesis, and the difference between hypothesized value, an observed value of the parameter due to fluctuation of the sample.
So the population parameter 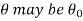
Case-2: when 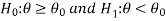 (left-tailed test)
(left-tailed test)
The rejection (critical) region falls under the left tail of the probability curve of the sampling distribution of test statistic Z.
Suppose -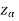 is the critical value at
is the critical value at 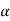 level of significance than the entire region less than or equal to -
level of significance than the entire region less than or equal to -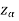 is the rejection region, and greater than -
is the rejection region, and greater than -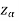 is the non-rejection region
is the non-rejection region
If z ≤-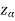 , that means the calculated value of test statistic Z lies in the rejection region, then we reject the null hypothesis H0 at
, that means the calculated value of test statistic Z lies in the rejection region, then we reject the null hypothesis H0 at 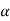 level of significance.
level of significance.
If z >- , that means the calculated value of test statistic Z lies in the non-rejection region, then we do not reject the null hypothesis H0 at
, that means the calculated value of test statistic Z lies in the non-rejection region, then we do not reject the null hypothesis H0 at 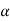 level of significance.
level of significance.
In the case of the two-tailed test-
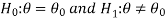
In this case, the rejection region falls under both tails of the probability curve of the sampling distribution of the test statistic Z. Half the area (α) i.e. α/2 will lie under the left tail, and the other half under the right tail. Suppose 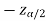 , and
, and 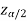 are the two critical values at the left-tailed, and right-tailed respectively. Therefore, an entire region less than or equal to
are the two critical values at the left-tailed, and right-tailed respectively. Therefore, an entire region less than or equal to 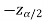 and greater than or equal to
and greater than or equal to  are the rejection regions, and between -
are the rejection regions, and between -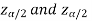 is the non-rejection region.
is the non-rejection region.
If Z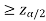 that means the calculated value of test statistic Z lies in the rejection region, then we reject the null hypothesis H0 at
that means the calculated value of test statistic Z lies in the rejection region, then we reject the null hypothesis H0 at  level of significance.
level of significance.
If 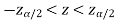 that means the calculated value of test statistic Z lies in the non-rejection region, then we do not reject the null hypothesis H0 at
that means the calculated value of test statistic Z lies in the non-rejection region, then we do not reject the null hypothesis H0 at 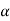 level of significance.
level of significance.
Testing of hypothesis for the population mean using Z-Test
For testing the null hypothesis, the test statistic Z is given as-
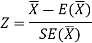
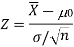
The sampling distribution of the test statistics depends upon variance 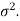
So that there are two cases-
Case-1: when 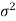 is known -
is known -
The test statistic follows the normal distribution with mean 0, and variance unity when the sample size is large as the population under study is normal or non-normal. If the sample size is small then test statistic Z follows the normal distribution only when the population under study is normal. Thus,
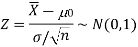
Case-2: when  is unknown –
is unknown –
We estimate the value of 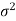 by using the value of sample variance
by using the value of sample variance
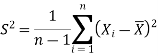
Then the test statistic becomes-

After that, we calculate the value of the test statistic as may be the case (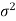 is known or unknown), and compare it with the critical value at the prefixed level of significance α.
is known or unknown), and compare it with the critical value at the prefixed level of significance α.
Example: A manufacturer of ballpoint pens claims that a certain pen manufactured by him has a mean writing-life of at least 460 A-4 size pages. A purchasing agent selects a sample of 100 pens and put them on the test. The mean writing-life of the sample found 453 A-4 size pages with a standard deviation of 25 A-4 size pages. Should the purchasing agent reject the manufacturer’s claim at a 1% level of significance?
Sol.
It is given that-
The specified value of the population mean = 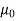 = 460,
= 460,
Sample size = 100
Sample mean = 453
Sample standard deviation = S = 25
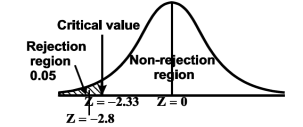
The null, and alternative hypothesis will be-

Also, the alternative hypothesis left-tailed so that the test is left tailed test.
Here, we want to test the hypothesis regarding population mean when population SD is unknown. So we should use a t-test for if the writing-life of the pen follows a normal distribution. But it is not the case. Since sample size is n = 100 (n > 30) large so we go for Z-test. The test statistic of Z-test is given by
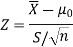
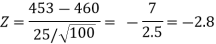
We get the critical value of left tailed Z test at 1% level of significance is 
Since the calculated value of test statistic Z (= ‒2.8,) is less than the critical value
(= −2.33), that means the calculated value of test statistic Z lies in the rejection region so we reject the null hypothesis. Since the null hypothesis is the claim so we reject the manufacturer’s claim at a 1% level of significance.
Example: A big company uses thousands of CFL lights every year. The brand that the company has been using in the past has an average life of 1200 hours. A new brand is offered to the company at a price lower than they are paying for the old brand. Consequently, a sample of 100 CFL light of new brand is tested which yields an average life of 1220 hours with a standard deviation of 90 hours. Should the company accept the new brand at a 5% level of significance?
Sol.
Here we have-
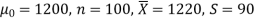
The company may accept the new CFL light when the average life of
CFL light is greater than 1200 hours. So the company wants to test that the new brand CFL light has an average life greater than 1200 hours. So our claim is 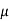 > 1200, and its complement is
> 1200, and its complement is 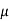 ≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis, and the claim as the alternative hypothesis. Thus,
≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis, and the claim as the alternative hypothesis. Thus,

Since the alternative hypothesis is right-tailed so the test is right-tailed.
Here, we want to test the hypothesis regarding population mean when population SD is unknown, so we should use a t-test if the distribution of life of bulbs known to be normal. But it is not the case. Since the sample size is large (n > 30) so we can go for a Z-test instead of a t-test.
Therefore, the test statistic is given by
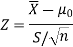
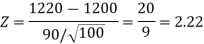
The critical values for a right-tailed test at a 5% level of significance is
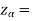 1.645
1.645
Since the calculated value of test statistic Z (= 2.22) is greater than the critical value (= 1.645), that means it lies in the rejection region so we reject the null hypothesis, and support the alternative hypothesis i.e. we support our claim at a 5% level of significance
Thus, we conclude that the sample does not provide us sufficient evidence against the claim so we may assume that the company accepts the new brand of bulbs
Level of significance-
The probability of type-1 error is called the level of significance of a test. It is also called the size of the test or the size of the critical region. Denoted by 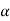 .
.
It is prefixed as a 5% or 1% level of significance.
If the calculated value of the test statistics lies in the critical region then we reject the null hypothesis.
The level of significance relates to the trueness of the conclusion. If the null hypothesis does not reject at level 5% then a person will be sure “concluding about the null hypothesis” is true with 95% assurance but even it may false with 5% chance.
The general procedure of t-test for testing hypothesis-
Let X1, X2,…, Xn be a random sample of small size n (< 30) selected from a normal population, having parameter of interest, say,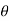
Which is unknown but its hypothetical value- then
Step-1: First of all, we set up null and alternative hypotheses
Step-2: After setting the null, and alternative hypotheses our next step is to decide criteria for rejection or non-rejection of null hypothesis i.e. decide the level of significance 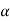 at which we want to test our null hypothesis. We generally take
at which we want to test our null hypothesis. We generally take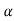 = 5 % or 1%.
= 5 % or 1%.
Step-3: The third step is to determine an appropriate test statistic, say, t for testing the null hypothesis. Suppose Tn is the sample statistic (maybe sample mean, sample correlation coefficient, etc. depending upon 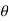 ) for the parameter
) for the parameter 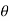 then test-statistic t is given by
then test-statistic t is given by
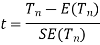
Step-4: As we know, the t-test is based on t-distribution, and t-distribution is described with the help of its degrees of freedom, therefore, test statistic t follows t-distribution with specified degrees of freedom as the case may be.
By putting the values of Tn, E(Tn), and SE(Tn) in the above formula, we calculate the value of test statistic t. Let t-cal be the calculated value of test statistic t after putting these values.
Step-5: After that, we obtain the critical (cut-off or tabulated) value(s) in the sampling distribution of the test statistic t corresponding to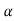 assumed in Step II. The critical values for the t-test are corresponding to a different level of significance (α). After that, we construct the rejection (critical) region of size
assumed in Step II. The critical values for the t-test are corresponding to a different level of significance (α). After that, we construct the rejection (critical) region of size 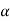 in the probability curve of the sampling distribution of test statistic t.
in the probability curve of the sampling distribution of test statistic t.
Step-6: Decide on the null hypothesis based on calculated, and critical value(s) of test statistic obtained in Step IV, and Step V respectively.
Critical values depend upon the nature of the test.
The following cases arise-
In the case of the one-tailed test-
Case-1: 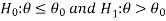 [Right-tailed test]
[Right-tailed test]
In this case, the rejection (critical) region falls under the right tail of the probability curve of the sampling distribution of test statistic t.
Suppose  is the critical value at
is the critical value at 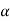 level of significance than the entire region greater than or equal to
level of significance than the entire region greater than or equal to 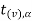 is the rejection region, and less than
is the rejection region, and less than 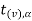 is the non-rejection region.
is the non-rejection region.
If 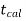 ≥
≥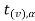 that means the calculated value of test statistic t lies in the rejection (critical) region, then we reject the null hypothesis
that means the calculated value of test statistic t lies in the rejection (critical) region, then we reject the null hypothesis 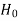 at
at 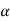 level of significance.
level of significance.
If 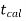 <
<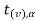 that means the calculated value of test statistic t lies in the non-rejection region, then we do not reject the null hypothesis
that means the calculated value of test statistic t lies in the non-rejection region, then we do not reject the null hypothesis 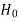 at
at 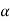 level of significance.
level of significance.
Case-2: 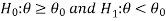 [Left-tailed test]
[Left-tailed test]
In this case, the rejection (critical) region falls under the left tail of the probability curve of the sampling distribution of test statistic t.
Suppose -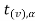 is the critical value at
is the critical value at 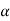 level of significance than the entire region less than or equal to -
level of significance than the entire region less than or equal to -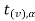 is the rejection region, and greater than -
is the rejection region, and greater than -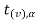 is the non-rejection region.
is the non-rejection region.
If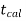 ≤ −
≤ −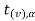 that means the calculated value of test statistic t lies in the rejection (critical) region, then we reject the null hypothesis
that means the calculated value of test statistic t lies in the rejection (critical) region, then we reject the null hypothesis 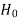 at
at 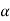 level of significance.
level of significance.
If 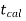 > −
> −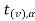 , that means the calculated value of test statistic t lies in the non-rejection region, then we do not reject the null hypothesis
, that means the calculated value of test statistic t lies in the non-rejection region, then we do not reject the null hypothesis 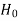 at
at 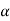 level of significance.
level of significance.
In the case of the two-tailed test-
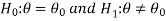
In this case, the rejection region falls under both tails of the probability curve of the sampling distribution of the test statistic t. Half the area (α) i.e. α/2 will lie under the left tail, and another half under the right tail. Suppose -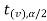 , and
, and 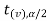 are the two critical values at the left- tailed, and right-tailed respectively. Therefore, an entire region less than or equal to -
are the two critical values at the left- tailed, and right-tailed respectively. Therefore, an entire region less than or equal to -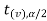 and greater than or equal to
and greater than or equal to 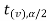 are the rejection regions, and between -
are the rejection regions, and between -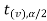 and
and 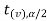 is the non-rejection region.
is the non-rejection region.
If 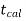 ≥
≥ 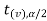 or
or 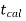 ≤ -
≤ - , that means the calculated value of test statistic t lies in the rejection(critical) region, then we reject the null hypothesis
, that means the calculated value of test statistic t lies in the rejection(critical) region, then we reject the null hypothesis 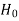 at
at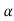 level of significance.
level of significance.
And if -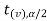 <
< 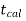 <
< 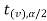 , that means the calculated value of test statistic t lies in the non-rejection region, then we do not reject the null hypothesis
, that means the calculated value of test statistic t lies in the non-rejection region, then we do not reject the null hypothesis 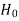 at
at 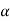 level of significance.
level of significance.
Testing of hypothesis for the population mean using t-Test
There are the following assumptions of the t-test-
- Sample observations are random, and independent.
- Population variance
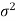 is unknown
is unknown - The characteristic under study follows a normal distribution.
For testing the null hypothesis, the test statistic t is given by-
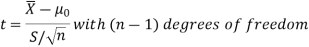
Example: A tyre manufacturer claims that the average life of a particular category
Of his tyre is 18000 km when used under normal driving conditions. A random sample of 16 tyres was tested. The mean, and SD of life of the tyres in the sample were 20000 km, and 6000 km respectively.
Assuming that the life of the tyres is normally distributed, test the claim of the manufacturer at a 1% level of significance using the appropriate test.
Sol.
Here we have-
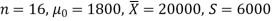
We want to test that manufacturer’s claim is true that the average
Life (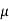 ) of tyres is 18000 km. So claim is μ = 18000, and its complement
) of tyres is 18000 km. So claim is μ = 18000, and its complement
Is μ ≠ 18000. Since the claim contains the equality sign so we can take
The claim as the null hypothesis, and complement as the alternative
Hypothesis. Thus,


Here, population SD is unknown, and the population under study is given to
Be normal.
So here can use t-test-
For testing the null hypothesis, the test statistic t is given by-
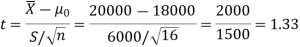
The critical value of test statistic t for two-tailed test corresponding (n-1) = 15 df at 1% level of significance are 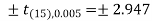
Since the calculated value of test statistic t (= 1.33) is less than the critical (tabulated) value (= 2.947), and greater than the critical value (= − 2.947), that means the calculated value of test statistic lies in the non-rejection region, so we do not reject the null hypothesis. We conclude that the sample fails to provide sufficient evidence against the claim so we may assume that manufacturer’s claim is true.
F-test-
Assumption of F-test-
The assumptions for F-test for testing the variances of two populations are:
- The samples must be normally distributed.
- The samples must be independent.
Let 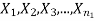 be a random sample of size
be a random sample of size 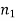 taken from a normal population with
taken from a normal population with  variance
variance 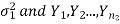 be a random sample of size
be a random sample of size 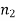 from another normal population with a mean
from another normal population with a mean 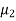 , and
, and 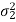 .
.
Here, we want to test the hypothesis about the two population variances so we can take our alternative null, and hypotheses as-
For two-tailed test-
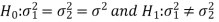
For one-tailed test-

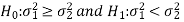
We use test statistic F for testing the null hypothesis-
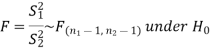
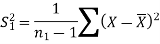
And

In the case of the one-tailed test-
Case-1: 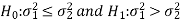 (right-tailed test)
(right-tailed test)
In this case, the rejection (critical) region falls at the right side of the probability curve of the sampling distribution of test statistic F. Suppose 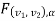 is the critical value of test statistic F with (
is the critical value of test statistic F with (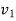 =
= 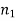 – 1,
– 1, 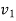 =
= 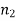 – 1) df at
– 1) df at 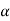 level of significance so entire region greater than or equal
level of significance so entire region greater than or equal 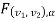 to is the rejection (critical) region, and less than
to is the rejection (critical) region, and less than 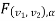 is the non-rejection region.
is the non-rejection region.
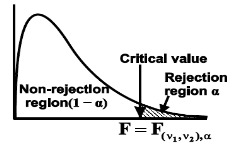
If  that means the calculated value of the test statistic lies in the rejection (critical) region, then we reject the null hypothesis H0 at
that means the calculated value of the test statistic lies in the rejection (critical) region, then we reject the null hypothesis H0 at level of significance. Therefore, we conclude that samples data provide us sufficient evidence against the null hypothesis, and there is a significant difference between population variances
level of significance. Therefore, we conclude that samples data provide us sufficient evidence against the null hypothesis, and there is a significant difference between population variances
If 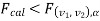 , that means the calculated value of the test statistic lies in the non-rejection region, then we do not reject the null hypothesis H0 at
, that means the calculated value of the test statistic lies in the non-rejection region, then we do not reject the null hypothesis H0 at 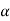 level of significance. Therefore, we conclude that the sample data fail to provide us sufficient evidence against the null hypothesis, and the difference between population variances due to fluctuation of the sample.
level of significance. Therefore, we conclude that the sample data fail to provide us sufficient evidence against the null hypothesis, and the difference between population variances due to fluctuation of the sample.
Case-2: 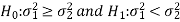 (left-tailed test)
(left-tailed test)
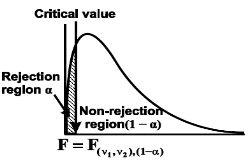
In this case, the rejection (critical) region falls at the left side of the probability curve of the sampling distribution of test statistic F. Suppose 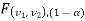 is the critical value at
is the critical value at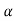 level of significance than the entire region less than or equal to
level of significance than the entire region less than or equal to 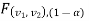 is the rejection(critical) region, and greater than
is the rejection(critical) region, and greater than 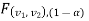 is the non-rejection region.
is the non-rejection region.
If 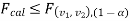 that means the calculated value of the test statistic lies in the rejection (critical) region, then we reject the null hypothesis H0 at
that means the calculated value of the test statistic lies in the rejection (critical) region, then we reject the null hypothesis H0 at 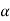 level of significance.
level of significance.
If 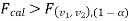 that means the calculated value of the test statistic lies in the non-rejection region, then we do not reject the null hypothesis H0 at
that means the calculated value of the test statistic lies in the non-rejection region, then we do not reject the null hypothesis H0 at 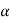 level of significance.
level of significance.
In the case of the two-tailed test-
When 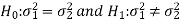
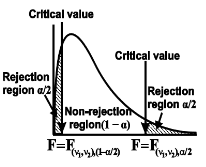
In this case, the rejection (critical) region falls at both sides of the probability curve of the sampling distribution of test statistic F, and half the area(α) i.e. α/2 of rejection (critical) region lies at the left tail and another half on the right tail.
Suppose  and
and 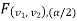 are the two critical values at the left-tailed, and right-tailed respectively on pre-fixed
are the two critical values at the left-tailed, and right-tailed respectively on pre-fixed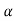 level of significance. Therefore, an entire region less than or equal to
level of significance. Therefore, an entire region less than or equal to 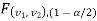 , and greater than or equal to
, and greater than or equal to 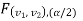 are the rejection (critical) regions, and between
are the rejection (critical) regions, and between  , and
, and 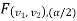 is the non-rejection region
is the non-rejection region
If  or
or 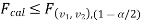 that means the calculated value of the test statistic lies in the rejection(critical) region, then we reject the null hypothesis H0 at the α level of significance.
that means the calculated value of the test statistic lies in the rejection(critical) region, then we reject the null hypothesis H0 at the α level of significance.
If 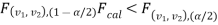 that means the calculated value of test statistic F lies in the non-rejection region, then we do not reject the null hypothesis H0 at α level of significance.
that means the calculated value of test statistic F lies in the non-rejection region, then we do not reject the null hypothesis H0 at α level of significance.
Example: Two sources of raw materials are under consideration by a bulb manufacturing company. Both sources seem to have similar characteristics but the company is not sure about their respective uniformity. A sample of 12 lots from source A yields a variance of 125, and a sample of 10 lots from source B yields a variance of 112. Is it likely that the variance of source A significantly differs from the variance of source B at significance level α = 0.01?
Sol.
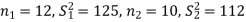
The null, and alternative hypothesis will be-
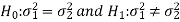
Since the alternative hypothesis is two-tailed so the test is two-tailed.
Here, we want to test the hypothesis about two population variances and sample sizes 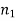 = 12(< 30), and
= 12(< 30), and 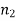 = 10 (< 30) are small. Also, the populations under study are normal, and both samples are independent.
= 10 (< 30) are small. Also, the populations under study are normal, and both samples are independent.
So we can go for F-test for two population variances.
The test statistic is-
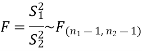
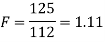
The critical (tabulated) value of test statistic F for the two-tailed test corresponding 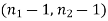 = (11, 9) df at 5% level of significance are
= (11, 9) df at 5% level of significance are 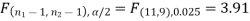 , and
, and
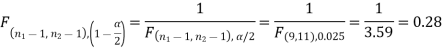
Since the calculated value of test statistic (= 1.11) is less than the critical value (= 3.91), and greater than the critical value (= 0.28), that means the calculated value of test statistic lies in the non-rejection region, so we do not reject the null hypothesis, and reject the alternative hypothesis. We conclude that samples provide us sufficient evidence against the claim so we may assume that the variances of source A and B differ.
Chi-square 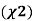 test
test
When a fair coin is tossed 80 times we expect from the theoretical considerations that heads will appear 40 times, and tail 40 times. But this never happens in practice that is the results obtained in an experiment do not agree exactly with the theoretical results. The magnitude of discrepancy between observations, and theory is given by the quantity 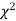 (pronounced as chi-squares). If
(pronounced as chi-squares). If 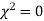 the observed, and theoretical frequencies completely agree. As the value of
the observed, and theoretical frequencies completely agree. As the value of 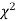 increases, the discrepancy between the observed, and theoretical frequencies increases.
increases, the discrepancy between the observed, and theoretical frequencies increases.
Definition. If 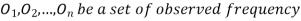 , and
, and 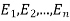 be the corresponding set of expected (theoretical) frequencies, then
be the corresponding set of expected (theoretical) frequencies, then 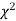 is defined by the relation
is defined by the relation
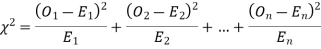
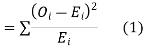
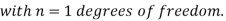
Chi-square distribution
If 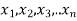 be n independent normal variates with mean zero, and s.d. Unity, then it can be shown that
be n independent normal variates with mean zero, and s.d. Unity, then it can be shown that 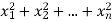 is a random variate having
is a random variate having 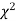 distribution with ndf.
distribution with ndf.
The equation of the 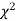 curve is
curve is
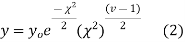
Properties of 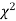 distribution
distribution
- If v = 1, the
 curve (2) reduces to
curve (2) reduces to 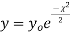 which is the exponential distribution.
which is the exponential distribution. - If
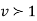 this curve is tangential to the x-axis at the origin and is positively skewed as the mean is at v and mode at v-2.
this curve is tangential to the x-axis at the origin and is positively skewed as the mean is at v and mode at v-2. - The probability P that the value of
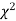 from a random sample will exceed
from a random sample will exceed 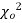 is given by
is given by
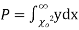
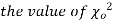 have been tabulated for various values of P, and values of v from 1 to 30. (Table V Appendix 2)
have been tabulated for various values of P, and values of v from 1 to 30. (Table V Appendix 2)
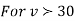 , the
, the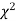 curve approximates to the normal curve, and we should refer to normal distribution tables for significant values of
curve approximates to the normal curve, and we should refer to normal distribution tables for significant values of 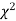 .
.
IV. Since the equation of 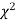 the curve does not involve any parameters of the population, this distribution does not dependent on the form of the population.
the curve does not involve any parameters of the population, this distribution does not dependent on the form of the population.
V. Mean = 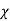 , and variance =
, and variance = 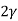
Goodness of fit
The values of 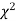 is used to test whether the deviations of the observed frequencies from the expected frequencies are significant or not. It is also used to test how well a set of observations fit given distribution
is used to test whether the deviations of the observed frequencies from the expected frequencies are significant or not. It is also used to test how well a set of observations fit given distribution 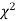 therefore provides a test of goodness of fit, and may be used to examine the validity of some hypothesis about an observed frequency distribution. As a test of goodness of fit, it can be used to study the correspondence between the theory, and fact.
therefore provides a test of goodness of fit, and may be used to examine the validity of some hypothesis about an observed frequency distribution. As a test of goodness of fit, it can be used to study the correspondence between the theory, and fact.
This is a nonparametric distribution-free test since in this we make no assumptions about the distribution of the parent population.
Procedure to test significance, and goodness of fit
(i) Set up a null hypothesis, and calculate
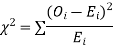
(ii) Find the df, and read the corresponding values of  at a prescribed significance level from table V.
at a prescribed significance level from table V.
(iii) From 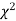 table, we can also find the probability P corresponding to the calculated values of
table, we can also find the probability P corresponding to the calculated values of 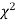 for the given d.f.
for the given d.f.
(iv) If P<0.05, the observed value of  is significant at a 5% level of significance
is significant at a 5% level of significance
If P<0.01 the value is significant at the 1% level.
If P>0.05, it is good faith, and the value is not significant.
Example. A set of five similar coins is tossed 320 times, and the result is
Number of heads | 0 | 1 | 2 | 3 | 4 | 5 |
Frequency | 6 | 27 | 72 | 112 | 71 | 32 |
Solution. For v = 5, we have 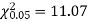
P, probability of getting a head=1/2;q, probability of getting a tail=1/2.
Hence the theoretical frequencies of getting 0,1,2,3,4,5 heads are the successive terms of the binomial expansion 
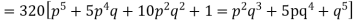
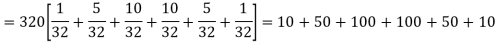
Thus the theoretical frequencies are 10, 50, 100, 100, 50, 10.
Hence, 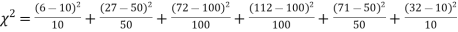
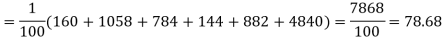
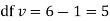
Since the calculated value of 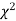 is much greater than
is much greater than 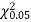 the hypothesis that the data follow the binomial law is rejected.
the hypothesis that the data follow the binomial law is rejected.
Example. Fit a Poisson distribution to the following data, and test for its goodness of fit at a level of significance 0.05.
x | 0 | 1 | 2 | 3 | 4 |
f | 419 | 352 | 154 | 56 | 19 |
Solution. Mean m =
Hence, the theoretical frequency is 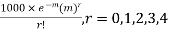
X | 0 | 1 | 2 | 3 | 4 | Total |
F | 404.9 (406.2) | 366 | 165.4 | 49.8 | 11..3 (12.6) | 997.4 |
Hence, 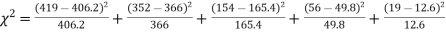
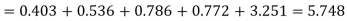
Since the mean of the theoretical distribution has been estimated from the given data, and the totals have been made to agree, there are two constraints so that the number of degrees of freedom v = 5- 2=3
For v = 3, we have 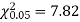
Since the calculated value of 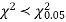 the agreement between the fact, and theory is good, and hence the Poisson distribution can be fitted to the data.
the agreement between the fact, and theory is good, and hence the Poisson distribution can be fitted to the data.
Example. In experiments of pea breeding, the following frequencies of seeds were obtained
Round, and yellow | Wrinkled, and yellow | Round, and green | Wrinkled, and green | Total |
316 | 101 | 108 | 32 | 556 |
Theory predicts that the frequencies should be in proportions 9:3:3:1. Examine the correspondence between theory, and experiment.
Solution. The corresponding frequencies are
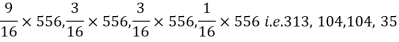
Hence,
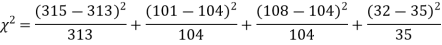
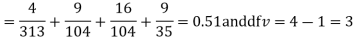
For v = 3, we have 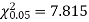
Since the calculated value of 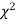 is much less than
is much less than 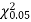 there is a very high degree of agreement between theory, and experiment.
there is a very high degree of agreement between theory, and experiment.
References:
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. N.P. Bali, and Manish Goyal, A textbook of Engineering Mathematics, Laxmi Publications.
3. P. G. Hoel, S. C. Port, and C. J. Stone, Introduction to Probability Theory, Universal Book Stall.
4. S. Ross, A First Course in Probability, 6th Ed., Pearson Education India,2002.