Unit - 1
Mathematical Logic
Introduction:
In unit we shall study mathematical logic, which is concerned with all kinds of reasoning.
Mathematical logic has two aspects. On one hand it is analytical theory of art of reasoning whose goal is to systematize and codify principles of valid reasoning. It may be used to judge the correctness of statements which make up the chain. In this aspect logic may be called ‘classical’ mathematical logic.
The other aspect of Mathematical logic is inter-related with problems relating the foundation of Mathematics. G. Frege (1884–1925) developed the idea, regarding a mathematical theory as applied system of logic.
Principles of logic are valuable to problem analysis, programming and logic design.
Statement-
When a declarative sentence which is true or false but not both is called statement.
The truth values “true” and “false” of a statement are denoted by T ad F respectively. We can denote them by 0 and 1 as well.
Examples of statements are-
1. 2 + 11 = 12
2. Jaipur is in India
Truth table-
The table showing the truth values of a statement formula is called ‘truth table’.
The truth table for a given statement form displays the truth values that correspond to all possible combinations of truth values for its component statement variables.
Laws of formal-
1. Law of contradiction- According to the law of contradiction the same predicate cannot be both affirmed and denied precisely of the same subject
For every preposition p is not the same that p is both true and false.
2. Law of excluded middle- If p is a statement, then either p is true or p is false and there cannot be middle ground.
Connectives-
Statements in mathematical logic are combinations of simpler statements joined by words and phrases like ‘and’. ‘or’, ‘if and only if’, etc. These words and phrases are called logical connectives.
Disjunction-
Definition: The disjunction of two propositions p and q is the compound statement 10 Elementary Logic p or q, denoted by p ∨ q.
For example, ‘Aman has a house or Amit has a house’ Is the disjunction of p and q, where-
p: Aman has a house, and
q: Amit has a house.
Example: Obtain the truth value of the disjunction of ‘The earth is flat’. And ‘3 + 5 = 2’.
Solution: Let p denote ‘The earth is flat,’ and q denote ‘3 + 5 = 2’. Then we know that the truth values of both p and q are F. Therefore, the truth value of p ∨ q is F.
Example-Let p: 5 + 2 = 7, q: 9 + 2 = 10 then p ∨q: 5 + 2 = 7 or 9 + 2 = 10
Truth table for disjunction-
p | q | p∨q |
T T F F | T F T F | T T T F |
Exclusive disjunction-
The exclusive disjunction of two propositions p and q is the statement ‘Either p is true or q is true, but both are not true. Either p is true or q is true, but both are not true’. We denote this by p ⊕q.
Conjunction-
Definition: We call the compound statement ‘p and q’ the conjunction of the
Statements p and q. We denote this by p ∧q.
Example- ‘3 + 1 ≠ 7 ∧ 2 > 0’ is the conjunction of ‘3 + 1 ≠ 7’ and ‘2 > 0’.
p | q | p∧q |
T T F F | T F T F | T F F F |
Example-
Obtain the truth value of the conjunction of ‘2 ÷5 = 1’ and ‘Ramesh is in Jaipur’.
Solution: Let p: 2 ÷5 = 1, and
q: Ramesh is in Jaipur.
Then the truth value of p is F. Therefore, from Table 3 you will find that the truth
Value of p ∧ q is F.
Negation-
The negation of a proposition p is ‘not p’, denoted by ~p.
Example-
If p is ‘Smriti is at the station.’, then ~ p is ‘Smriti is not at the station’.
Similarly, if p is ‘No person can live without food.’,~ p is ‘At least one person can live without food.’
Conditional connectives-
Given any two propositions p and q, we denote the statement ‘If p, then q’ by
p→ q. We also read this as ‘p implies q’. Or ‘p is sufficient for q’, or ‘p only if q’. We also call p the hypothesis and q the conclusion. Further, a statement of the form p → q is called a conditional statement.
Truth table for implication-
p | q | p q |
T T F F | T F T F | T F T T |
Definition for converse-
The converse of p → q is q → p. In this case we also say ‘p is necessary for q’, or ‘p if q’ when we combine an implication and its converse, then-
Let p and q be two propositions. The compound statement
(p→ q) ∧(q → p) is the bi-conditional of p and q. We denote it by p ↔ q, and (Read) as ‘p if and only q’.
We use ‘if and only ‘if’ as iff
We also say that ‘p implies and is implied by q’. Or ‘p is necessary and sufficient for q’.
Example- Pradeep will get good marks if and only if he studies regularly means that Pradeep will get good marks if he studies regularly and Pradeep studies regularly if he gets good marks.
Truth table for two-way implication-
p | q | p q | q p | p ↔ q |
T T F F | T F T F | T F T T | T T F T | T F F T |
Disjunctive normal form-
Definition-
Suppose A denotes a given formula. Another formula B which is equivalent to A will be called a disjunctive normal form of A if B is a sum of elementary products.
A disjunctive normal form of a given formula is constructed as given below-
(i) Replace ‘→’, ‘↔’ by using the logical connectives ∧, ∨and ~.
(ii) Use De Morgan’s laws to eliminate ~ before sums or products.
(iii) Apply distributive laws repeatedly and eliminate product of variables to obtain the required normal form.
Example: Obtain disjunctive normal form ofp∨(~p →(q ∨(q →~r)))
Solution: p ∨(~p →(q ∨(q →~r)))
≡p ∨(~p →q ∨(~q ∨~r)))
≡p∨(p ∨(q ∨(~q ∨~r)))
≡p∨p∨q ∨~q ∨~r
≡p∨q∨~q ∨~r
Therefore, the disjunctive normal form of
p∨(~p →(q ∨( ~q →~r))) is p ∨q ∨~q ~r
Example: Obtain the disjunctive normal form of
(a) p∨(~p →(q ∨(q →~r)))
Solution:
(a) p∨(_ p →(q ∨(q →_ r)))
≡p∨(_ p →q ∨(_ q ∨_ r))
≡p∨( p∨q ∨(_ q ∨_ r))
≡p∨p∨q ∨_ q ∨_ r
≡p∨q∨_ q ∨_ r
Conjunctive normal form-
Let A denote a given formula, another formula B which is equivalent to A is called conjunctive normal formula if B is a product of an elementary sum.
Principal disjunctive normal form-
Definition 1.5: If A is a given formula, then an equivalent formula B, consisting of disjunctives of Minterms only is called the Principal disjunctive normal form of the formula A.
Example: Obtain the principal disjunctive normal form of (~ p ∨~ q)→ (~ p ∧r).
Solution: (~ p ∨~ q)→ (~ p ∧r )
⇔~(~ p ∨~ q) ∨ (~ p ∧r )
⇔~ (~(p ∧q)) ∨ (~ p ∧r )
⇔( p∧q) ∨ (~ p ∧r )
⇔( p∧q∧ (r ∨~ r )) ∨ (~ p ∧r ∧ (q ∨~ q))
⇔( p∧q∧r) ∨ ( p ∧q ∧~ r) ∨ (~ p ∧r ∧q) ∨ (~ p ∧r ∧~ q)
The principal disjunctive normal form of the given formula is
( p∧q∧r) ∨( p∧q∧~ r) ∨ (~ p ∧q ∧r) ∨ (~ p ∧~ q ∧r)
Example: Obtain the principal disjunctive normal form of ~p ∨q.
Solution: ~p ∨q ≡(~p ∧(q ∨~q)) ∨(q ∧(p ∨~p))
≡(~p ∧q) ∨(~p ∧~q) ∨(q ∧p) ∨(q ∧~p)
≡(~p ∧q) ∨(~p ∧~q) ∨(p ∧q)
Therefore (~p ∧q) ∧(~p ∧~q) ∧(p ∧q) is the required principal disjunctive normal form.
Principal conjunctive normal form-
Definition 1.6: If A is a given formula, then an equivalent formula B is called principle conjunctive normal form of A if B is a product of maxterms.
Theory of inference of statement calculus-
Modus ponens and modus tollens-
An argument form consisting of two premises and a conclusion is called a syllogism. The first and second premises are called the major premise and minor premise, respectively.
The most famous form of syllogism in logic is called modus ponens. It has the following form:
If p then q.
p
∴q
Example:
If the sum of the digits 469437 is divisible by 3
Then 469437 is divisible by 3.
The another valid argument form called modus tollens.
Modus tollens means- method of denying.
It has the following form-
If p then q.
∼q
∴∼p
For example-
If Rahim is tall, then Rahim is thick.
Rahim is not thick.
∴Rahim is not tall.
The rules of inference- (Modus ponens and modus tollens)
The theory of inference is a form of argument that is valid.
Modus ponens and modus tollens are both rules of inference.
The following result gives the rules of inference-
Implications:
I1 P ∧ Q P (Simplification)
I2 P ∧ Q Q (Simplification)
I3 P P ∨ Q (Addiction)
I4 Q P ∨ Q (Addiction)
I5 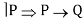
I6 Q P Q
I7 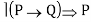
I8 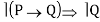
I9 P, Q P ∧ Q
I10 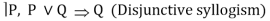
I11 P, P Q Q (Modus Ponens)
I12 
I13 P Q, Q R P R (Hypothetical syllogism)
I14 P ∨ Q, P R, Q R R (Dilemma)
Equivalences:
E1 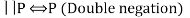
E2 P ∧ Q 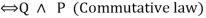
E3 P ∨ Q  Q ∨ P (Commutative law)
Q ∨ P (Commutative law)
E4 (P ∧ Q) ∧ R  P ∧ (Q ∧ R) (Associative law)
P ∧ (Q ∧ R) (Associative law)
E5 (P ∨ Q) ∨ R ⟺ P ∨ (Q ∨ R) (Associative law)
E6 P ∧ (Q ∨ R) ⟺ (P ∧ Q) ∨ (P ∧ R) (Distributive law)
E7 P ∨ (Q ∧ R) ⟺ (P ∨ Q) ∧ (P ∨ Q) (Distributive law)
E8 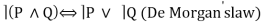
E9 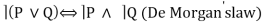
E10 P ∨ P  P
P
E11 P ∧ P  P
P
E12 R ∨ ( P ∧ 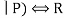
E13 R ∧ ( P ∨ 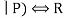
E14 R ∨ ( P ∧ 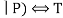
E15 R ∧ ( P ∧ 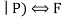
E16 P Q 
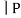 ∨ Q
∨ Q
E17 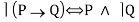
E18 P Q 
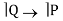
E19 P ( Q R) 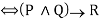
E20 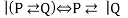
E21 P ⇄ Q ⇔ ( P Q) 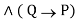
E22 (P ⇄ Q) ⇔ (P 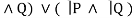
1. Modus ponens (Law of detachment)-
Let us consider the following argument-
If Ravi can fire, he will hit the target
Ravi can fire,
Therefore, he will hit the target.
In order to study the form of the argument, suppose p be the proposition ‘Ravi can fire’ and q be the proposition ‘ Ravi will hit the target’.
Then the premises are p→q and p.
The conclusion is q.
Hence the form of argument-
Hence the form of argument-
p q
p/q, i.e., [ (p q) ∧ p] q
To check the validity of this argument we will construct a truth table as follows-
p | q | p q | (p q) ∧ q |
T T F F | T F T F | T F T T | T F F F |
By looking the second column(the conclusion) and the fourth column(the premises).
Whenever the premises are true in first row the conclusion is true.
Hence the argument is valid.
This is the form of valid argument and this law is called law of detachment because the conclusion q is detached from a premise.
We also call it as the law of direct inference.
2. Modus tollens (Law of detachment)-
Let us consider the following argument-
If Ravi can fire, he will hit the target.
Ravi will not hit the target.
Therefore, Ravi cannot fire.
The argument is of the form-
p q
~ q, i.e., [(p q) ∧ ∼ ] ∼ p
As we know that, we read in grammar predicate is the word in a sentence which expresses what is said of the object. It is a part of a declarative sentence describing the properties of an object or relation among objects.
It is a part of a declarative sentence describing the properties of an object or relation among objects (The word ‘Predicate’ and property will be used to mean the same thing) for example ‘is a cricket player’, ‘is a teacher’ ‘is short’ are predicates. In logic the word predicate has a broader role than in grammar. The basis for this is the observation that a predicate is supplemented by, including a variable x as a place holder, for the intended subject, the result behaves as ‘a statement function’, in the sense that for each value of x a statement results. Consider the statement p : x is an even number
The truth value of p depends on the value of x. p is true when x = 4, and false when x = 11. The statement p is not a proposition. In this section we extend the system of logic to include such statements.
In grammar ‘Rajan loves’ is not a predicate. If ‘x’ is introduced as a place holder for the object, then we get the result as ‘Rajan loves x’.
Which is a statement function. Thus we can define, a predicate p(x) as an expression having the quality that on an assignment of values to the variable x, from an appropriate domain, a statement results.
Def: Let P (x) be a statement involving variable x and a set D. We call P a propositional function if for each x in D, P (x) is a proposition. The set D is called the domain of discourse (or universe of discourse) of P. It is the set of all possible values which can be assigned to variables in statements involving predicates.
For example the domain of discourse for P (x): “x is a cricket player” can be taken as the set of all human beings and the statement.
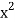 – 3x – 7 = 0
– 3x – 7 = 0
Is a propositional function. The domain of discourse is the set of real numbers.
In logic it has a wide role.
A predicate is an expression of one or more variables defined on some specific domain. A predicate with variables can be made a proposition by either assigning a value to the variable or by quantifying the variable.
The following are some examples of predicates −
- Let E (x, y) denote "x = y"
- Let X (a, b, c) denote "a + b + c = 0"
- Let M (x, y) denote "x is married to y"
A series of claims is referred to as an argument. The conclusion is the last assertion, and the premises are the ones before it (or hypothesis). Before the conclusion, the symbol "∴" (read thus) is placed. The conclusion of a valid argument flows from the truth values of the premises.
The templates or instructions for creating valid arguments from the statements we already know are provided by Rules of Inference.
Simple arguments can be used as the foundation for more complex valid arguments. Certain simple arguments that have been proven to be true are extremely essential in terms of their application. These are known as Rules of Inference arguments.
The most widely used Inference Rules are listed below —
Rules of Inference | Tautological form | Name |
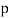 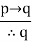 | 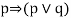 | Modus Ponens |
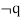 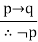
| 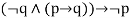 | Modus Tollens |
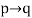 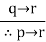 | 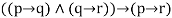 | Hypothetical syllogism |
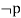 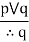 | 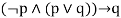
| Disjunctive syllogism |
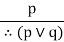 | 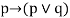 | Addition |
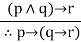 | 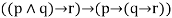 | Exportation |
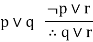 | 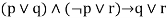 | Resolution |
Similarly, we have Rules of Inference for quantified statements –
Rule of Inference | Name |
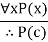 | Universal instantiation |
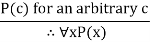 | Universal generalization |
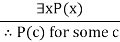 | Existential instantiation |
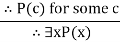 | Existential generalization |
References:
1. Discrete Mathematics and its Applications, Kenneth H. Rosen, 7th Edition, McGraw Hill Education (India) Private Limited.
2. Discrete Mathematics D.S. Malik & K. K. Sen, Revised Edition Cengage Learning.
3. Elements of Discrete Mathematics, C.L. Liu and D.P. Mohapatra, 4th Edition, McGraw Hill Education (India) Private Limited.
4. Discrete Mathematics with Applications, Thomas Koshy, Elsevier.
5. Discrete and Combinatorial Mathematics, R. P. Grimaldi, Pearson.