Unit - 4
Turing Machine
An information processing system (TM) may be a mathematical model that consists of
Associate infinite length tape divided into cells on which input is given. It consists of a head that reads the input tape.
A state register stores the state of the information processing system. Once reading an associated input image, it’s replaced with another image, its internal state is modified, and it moves from one cell to the proper or left. If the metal reaches the ultimate state, the input string is accepted, otherwise rejected.
Formal definition
A metal will be formally delineate as a 7-tuple (Q, X, ∑, δ, q0, B, F)
Where −
• Q may be a finite set of states
• X is that the tape alphabet
• ∑ is that the input alphabet
• δ may be a transition function; δ: alphabetic character × X → alphabetic character × X ×
• q0 is that the initial state
• B is that the blank image
• F is that the set of ultimate states
Basic model of Turing machine
With the help of the following representation, the turning machine can be modelled.
1. The input tape contains an infinite number of cells, each cell containing one input symbol, so it is possible to position the input string on the tape. Blank characters fill up the empty tape.

Fig 1: Input tape
2. The finite control and the head of tape that is responsible for reading the current symbol of input. The head of the tape will switch from left to right,
3. A finite set of states through which the system has to go through.
4. Finite set of symbols that are used in the construction of the Turing machine logic, called external symbols.
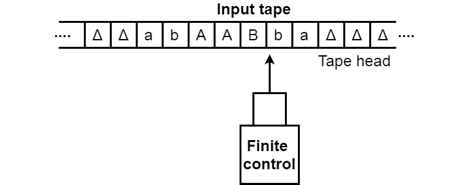
Fig 2: Basic model of TM
Various features of the Turing machine exist:
- It has an external memory that recalls an arbitrary, long input list.
- It has infinite capability for memory.
- The model has a method in which it is easy to read the input on the tape on the left or right.
- Depending on its input, the computer may generate a certain output. It will often be appropriate for the same input to be used to produce the output. So, the distinction between input and output has been abolished in this machine. It is therefore possible to use a standard set of alphabets for the Turing machine.
Key takeaway:
- TM may be a mathematical model that consists of associate infinite length tape divided into cells on which input is given.
- It consists of a head that reads the input tape.
- A state register stores the state of the information processing system.
1. Multiple tracks Alan Turing Machine:
- A k-tack Alan Turing machine(for some k>0) has k-tracks and one R/W head that reads and writes all of them one by one.
- A k-track information processing system may be simulated by one track information processing system
2. Two-way infinite Tape Alan Turing Machine:
- Infinite tape of two-way infinite tape information processing system is boundless in each directions left and right.
- Two-way infinite tape information processing system may be simulated by unidirectional infinite {turing|Turing|Alan Alan Turing|Alan Mathison Turing|mathematician} machine(standard Turing machine).
3. Multi-tape Alan Turing Machine:
- It has multiple tapes and controlled by one head.
- The Multi-tape information processing system is completely different from k-track information processing system however communicative power is same.
- Multi-tape information processing system may be simulated by single-tape information processing system.
4. Multi-tape Multi-head Alan Turing Machine:
- The multi-tape information processing system has multiple tapes and multiple heads
- Each tape controlled by separate head
- Multi-Tape Multi-head information processing system may be simulated by normal information processing system.
5. Multi-dimensional Tape Alan Turing Machine:
- It has multi-dimensional tape wherever head will move any direction that's left, right, up or down.
- Multi-dimensional tape information processing system may be simulated by one-dimensional information processing system.
6. Multi-head Alan Turing Machine:
- A multi-head information processing system contain 2 or additional heads to scan the symbols on constant tape.
- In one step all the heads sense the scanned symbols and move or write severally.
- Multi-head information processing system may be simulated by single head information processing system.
7. Non-deterministic Alan Turing Machine:
- A non-deterministic information processing system encompasses a single, a method infinite tape.
- For a given state and input image has atleast one option to move (finite range of decisions for consecutive move), every selection many decisions of path that it'd follow for a given input string.
- A non-deterministic information processing system is adored settled information processing system.
The Turing machine is a mathematical model of a machine that operates mechanically on a tape. There are symbols on this tape that the machine can read and write one at a time with the help of a tape head. The operation is entirely determined by a finite set of elementary instructions such as "write a 1 in state 42 if the symbol seen is 0; change to state 17 if the symbol seen is 1; write a 1 in state 17 if the symbol seen is 0 and change to state 6;" and so on. Turing imagines a person, whom he calls the "computer," who performs these deterministic mechanical laws slavishly in the original essay ("On Computable Numbers, with an Application to the Entscheidungs problem").
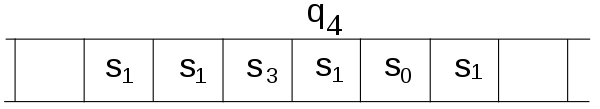
Fig 3: The instruction to be performed (q4) is shown over the scanned square
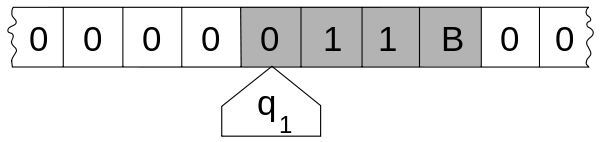
Fig 4: The internal state (q1) is shown inside the head, and the illustration describes the tape as being infinite and pre-filled with "0", the symbol serving as blank.
A Turing machine is made up of the following components:
- A tape with cells that are stacked one on top of the other. A symbol from a finite alphabet is contained in each cell. A specific blank symbol (here spelled as '0') and one or more other symbols make up the alphabet. The tape is supposed to be extensible to the left and right arbitrarily, ensuring that the Turing machine has access to as much tape as it requires for computing. The blank symbol is supposed to be filled in cells that have not been written in before. In some models, the tape has a specific symbol on the left end, and it extends or is infinitely extensible to the right.
- A head that can read and write symbols on the tape as well as move the tape left and right one cell at a time. In certain types, the tape is stationary while the head moves.
- A state register that stores the state of one of a finite number of Turing machines. The special start state with which the state register is initialized is one of them. These states, according to Turing, take the place of the "state of mind" that a person conducting calculations would be in.
- Given the present state(qi) of the machine and the symbol(aj) it is reading on the tape (symbol now under the head), a finite table of instructions directs the machine to do the following in order (for the 5-tuple models):
- Either delete or add a symbol (replacing aj with aj1).
- Move the head (which can take values of 'L' for one step left, 'R' for one step right, or 'N' for staying in the same spot, as indicated by dk).
- Assume the same or a different condition as directed (go to state qi1).
A multi-track non-deterministic Turing machine with a tape of some limited finite length is a linear bounded automaton.
Length = function (Length of the initial input string, constant c)
Here,
Memory information ≤ c × Input information
The measurement is limited to the region bounded by constants. There are two special symbols in the input alphabet that act as left end markers and right end markers, indicating that the transitions do not switch either to the left of the left end marker or to the right of the tape's right end marker.
A linear bounded automaton can be defined in 8-tuple -
(Q, X, ∑, q0, ML, MR, δ, F)
Where
- Q is a finite set of states
- X is the tape alphabet
- ∑ is the input alphabet
- q0 is the initial state
- ML is the left end marker
- MR is the right end marker where MR ≠ ML
- δ is a transition function which maps each pair (state) to (state, tape symbol, Constant ‘c’) where c could become 0 or +1 or -1.
- F is the set of final states.
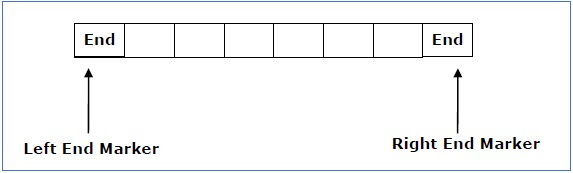
Fig 5: Linear bounded automata
Note -
- The measurement is limited to the region bounded by constants.
- A linear bounded automaton is a multi-track non-deterministic Turing machine with a tape of some limited finite length.
References:
1. Theory of Automata and Formal Language, R.B. Patel & P. Nath, Umesh Publication.
2. An Introduction and Finite Automata Theory, Adesh K. Pandey, TMH.
3. Theory of Computation AM Natrajan, Tamilarasi, Bilasubramani, New Age International Publishers, Chhattisgarh Swami Vivekan.
4. An introduction to Formal Languages and Automata by Peter Linz, Narosa Publications.