Unit - 3

Concurrency and Synchronization

3.1 Process synchronization

Process Synchronization is the task of coordinating the execution of processes in a way that no two processes can have access to the same shared data and resources.

It is specially needed in a multi-process system when multiple processes are running together, and more than one processes try to gain access to the same shared resource or data at the same time.

This can lead to the inconsistency of shared data. So the change made by one process not necessarily reflected when other processes accessed the same shared data. To avoid this type of inconsistency of data, the processes need to be synchronized with each other.

How Process Synchronization Works?

For Example, process A changing the data in a memory location while another process B is trying to read the data from the same memory location. There is a high probability that data read by the second process will be erroneous.

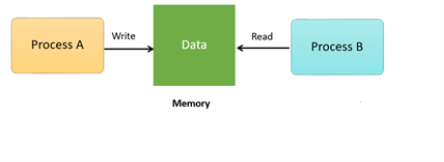
Fig 1 – Memory

Sections of a Program

Here, are four essential elements of the critical section:

●        Entry Section: It is part of the process which decides the entry of a particular process.

●        Critical Section: This part allows one process to enter and modify the shared variable.

●        Exit Section: Exit section allows the other process that are waiting in the Entry Section, to enter into the Critical Sections. It also checks that a process that finished its execution should be removed through this Section.

●        Remainder Section: All other parts of the Code, which is not in Critical, Entry, and Exit Section, are known as the Remainder Section.

Key takeaway

Process Synchronization is the task of coordinating the execution of processes in a way that no two processes can have access to the same shared data and resources.

It is specially needed in a multi-process system when multiple processes are running together, and more than one processes try to gain access to the same shared resource or data at the same time.

3.2 Critical section problem, and its solutions

The critical Section is the part of a program that tries to access shared resources. That resource is also any resource in a very pc sort of a memory location, organization, computer hardware, or any IO device.

The vital section can not be dead by quite one method at an identical time; software faces difficulties in permitting and disallowing the processes from coming into the vital section.

The vital section downside is employed to style a group of protocols which might make sure that the Race condition among the processes can ne'er arise.

To synchronize the cooperative processes, our main task is to resolve the vital section downside. We want to supply an answer in such a way that the subsequent conditions are glad.

Requirements of Synchronization mechanisms

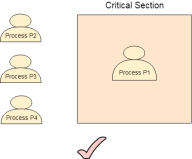
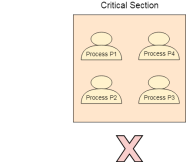
Fig 2 - Synchronization mechanisms

1. Progress

Progress means that if one process doesn't need to execute into a critical section then it should not stop other processes to get into the critical section.

2.     Bounded Waiting

We should be able to predict the waiting time for every process to get into the critical section. The process must not be endlessly waiting for getting into the critical section.

3.     Architectural Neutrality

Our mechanism must be architectural natural. It means that if our solution is working fine on one architecture then it should also run on the other ones as well.

Key takeaway

The critical Section is the part of a program that tries to access shared resources. That resource is also any resource in a very pc sort of a memory location, organization, computer hardware, or any IO device.

The vital section can not be dead by quite one method at an identical time; software faces difficulties in permitting and disallowing the processes from coming into the vital section.

3.3 Semaphores

Semaphores are integers variables that are utilized to provide solution to the critical section problem.

A semaphore is represented by S and apart from initialization it is utilize by two atomic operations, wait( ) and signal( ) for process synchronization.

Wait( ): The wait operation decreases the value of S, in case it is positive. On the other hand in case S is negative or zero, at that point no activity is performed.

Wait(S)

{

While (S<=0);

S- - ;

}

Signal( ): The signal( ) operation increases the value of its semaphore S.

Signal(S)

{

S++;

}

All changes to the integer value of the semaphore in the wait () and signal() function must be executed individually. That is, the point at which one process adjusts the semaphore value, no other process can at the same time change that equivalent semaphore value.

Furthermore, on account of wait (S), the testing of the integer value of (S ≤ 0), with its conceivable adjustment (S- - ), must be executed without interruption.

Properties of Semaphores

●        It's basic and consistently have a non-negative integer value.

●        Works with numerous processes.

●        Can have a wide range of critical section with various semaphores.

●        Each critical section has exceptional access semaphores.

●        Can allow numerous processes into the critical section at the same time, if desirable.

Types of Semaphores

There are two primary categories of semaphores for example counting semaphores and binary semaphores. Insights regarding these are given as below:

1. Counting Semaphores: These are integer number value semaphores and have an unlimited value space. These semaphores are utilized to facilitate the resource access, where the semaphore count is the quantity of accessible resources. On the off chance that the resources are added, semaphore count naturally increases and if the resources are removed, the count is decremented.
2. Binary Semaphores: The binary semaphores resemble counting semaphores yet their value is limited to 0 and 1. The wait( ) function possibly works when the semaphore is 1 and the signal operation succeeds when semaphore is 0. It is sometimes simpler to execute binary semaphores than counting semaphores.

Semaphore Usage

●        In practice, semaphores can take on one of two structures:

●        Binary semaphores can have one of the two values, 0 or 1. They can be utilized to provide solution to the critical section problem as portrayed above, and can be utilized as mutexes on systems that don't give a different mutex mechanism. The utilization of mutexes for this reason is given in figure below.

Do {

Waiting (mutex);

// critical section

Signal (mutex);

//remainder section

} while (true);

Mutual-exclusion usage with semaphores

●        Counting semaphores can take on any integer value, and are generally used to count the remaining number of some resource. The counter is defined to the value of such resources available in the system, and at point the counting semaphore is more than zero, at that point a process can enter a critical section and utilize one of the resources. When the counter gets up to zero (or negative in certain executions), then the process obstructs another process free a resource and increase the counting semaphore with a signal call.

Semaphores can likewise be utilized to synchronize certain tasks between processes. For instance, assume it is significant that process P1 execute instruction S1 before process P2 executes instruction S2.

●        First we make a semaphore named sync that is shared by the two processes, and defined it to zero.

●        At that point in process P1 we embed the code:

S1;

Signal( sync );

●        And in process P2 we embed the code:

Wait( sync );

S2;

●        Since sync was initialized to 0, process P2 will block on the wait until P1 executes the call to signal.

Advantages of Semaphores

Some of the benefits of semaphores are as per the following:

1. Semaphores permit just one process into the critical section. They follow the mutual exclusion standard carefully and are substantially more effective than some different techniques for synchronization.
2. There is no resource wastage in view of busy waiting in semaphores as processor time isn't wasted pointlessly to check if a condition is satisfied to enable a process to get to the critical section.
3. Semaphores are implemented in the machine independent code of the microkernel. So they are machine independent.

Disadvantages of Semaphores

Some of the disadvantages of semaphores are as per the following:

1. Semaphores are complicated so the wait and signal function must be designed in the right order to avoid deadlocks.
2. Semaphores are unfeasible for last scale use as their utilization prompts loss of modularity. This happens in light of the fact that the wait and signal tasks avoid the formation of an organized design for the system.
3. Semaphores may prompt a priority inversion where low priority processes may access the critical section first and high priority processes later.

Key takeaway

Semaphores are integers variables that are utilized to provide solution to the critical section problem.

3.4 Classical problems of synchronization: readers and writers problem

READERS WRITERS PROBLEM

The readers-writers problem is a classical problem of process synchronization, it relates to a data set such as a file that is shared between more than one process at a time. Among these various processes, some are Readers - which can only read the data set; they do not perform any updates, some are Writers - can both read and write in the data sets.

The readers-writers problem is used for managing synchronization among various reader and writer process so that there are no problems with the data sets, i.e. no inconsistency is generated.

Let's understand with an example - If two or more than two readers want to access the file at the same point in time there will be no problem. However, in other situations like when two writers or one reader and one writer wants to access the file at the same point of time, there may occur some problems, hence the task is to design the code in such a manner that if one reader is reading then no writer is allowed to update at the same point of time, similarly, if one writer is writing no reader is allowed to read the file at that point of time and if one writer is updating a file other writers should not be allowed to update the file at the same point of time. However, multiple readers can access the object at the same time.

Let us understand the possibility of reading and writing with the table given below:

TABLE 1

The solution of readers and writers can be implemented using binary semaphores.

We use two binary semaphores "write" and "mutex", where binary semaphore can be defined as:

Semaphore: A semaphore is an integer variable in S, that apart from initialization is accessed by only two standard atomic operations - wait and signal, whose definitions are as follows:

1. Wait(S)  
2. {  
3. While(S <= 0) ;  
4. S--;  
5. }  
6.  
7. 2. signal(S)  
8. {  
9. S++;  
10. }  

From the above definitions of wait, it is clear that if the value of S <= 0 then it will enter into an infinite loop (because of the semicolon; after while loop). Whereas the job of the signal is to increment the value of S.

The below code will provide the solution of the reader-writer problem, reader and writer process codes are given as follows -

Code for Reader Process

The code of the reader process is given below -

1. Static int readcount = 0;  
2. Wait (mutex);  
3. Readcount ++; // on each entry of reader increment readcount  
4. If (readcount == 1)  
5. {  
6.  Wait (write);  
7. }  
8. Signal(mutex);  
9.  
10. --READ THE FILE?  
11.  
12. Wait(mutex);  
13. Readcount --; // on every exit of reader decrement readcount  
14. If (readcount == 0)  
15. {  
16.  Signal (write);  
17. }  
18. Signal(mutex);  

In the above code of reader, mutex and write are semaphores that have an initial value of 1, whereas the read count variable has an initial value as 0. Both mutex and write are common in reader and writer process code, semaphore mutex ensures mutual exclusion and semaphore write handles the writing mechanism.

The read count variable denotes the number of readers accessing the file concurrently.

The moment variable read count becomes 1, wait operation is used to write semaphore which decreases the value by one. This means that a writer is not allowed how to access the file anymore. On completion of the read operation, read count is decremented by one. When read count becomes 0, the signal operation which is used to write permits a writer to access the file.

Code for Writer Process

The code that defines the writer process is given below:

1. Wait(write);  
2. WRITE INTO THE FILE  
3. Signal(wrt);  

If a writer wishes to access the file, wait operation is performed on write semaphore, which decrements write to 0 and no other writer can access the file. On completion of the writing job by the writer who was accessing the file, the signal operation is performed on write.

Let's see the proof of each case mentioned in Table 1

CASE 1: WRITING - WRITING → NOT ALLOWED. That is when two or more than two processes are willing to write, then it is not allowed. Let us see that our code is working accordingly or not?

Explanation:  

1. The initial value of semaphore write = 1  
2. Suppose two processes P0 and P1 wants to write, let P0 enter first the writer code, the moment P0 enters  
3. Wait(write); will decrease semaphore write by one, now write = 0  
4. And continue WRITE INTO THE FILE  
5. Now suppose P1 wants to write at the same time (will it be allowed?) let's see.  
6. P1 does Wait(write), since the write value is already 0, therefore from the definition of wait, it will go into an infinite loop (i.e. Trap), hence P1 can never write anything, till P0 is writing.  
7. Now suppose P0 has finished the task, it will  
8. Signal(write); will increase semaphore write by 1, now write = 1  
9. If now P1 wants to write it since semaphore write > 0  
10. This proofs that, if one process is writing, no other process is allowed to write.  

CASE 2: READING - WRITING → NOT ALLOWED. That is when one or more than one process is reading the file, then writing by another process is not allowed. Let us see that our code is working accordingly or not?

Explanation:  

1. Initial value of semaphore mutex = 1 and variable readcount = 0  
2. Suppose two processes P0 and P1 are in a system, P0 wants to read while P1 wants to write, P0 enter first into the reader code, the moment P0 enters   
3. Wait(mutex); will decrease semaphore mutex by 1, now mutex = 0  
4. Increment readcount by 1, now readcount = 1, next  
5. If (readcount == 1)// evaluates to TRUE  
6. {  
7.  Wait (write); // decrement write by 1, i.e. write = 0(which     
8.                   Clearly proves that if one or more than one   
9.                   Reader is reading then no writer will be    
10.                   Allowed.  
11. }  
12.  
13. Signal(mutex); // will increase semaphore mutex by 1, now mutex = 1 i.e. other readers are allowed to enter.  
14.  
15. And reader continues to --READ THE FILE?  
16.  
17. Suppose now any writer wants to enter into its code then:  
18.  
19. As the first reader has executed wait (write); because of which write value is 0, therefore wait(writer); of the writer, code will go into an infinite loop and no writer will be allowed.  
20. This proofs that, if one process is reading, no other process is allowed to write.  
21. Now suppose P0 wants to stop the reading and wanted to exit then  
22. Following sequence of instructions will take place:  
23. Wait(mutex); // decrease mutex by 1, i.e. mutex = 0  
24. Readcount --; // readcount = 0, i.e. no one is currently reading  
25. If (readcount == 0) // evaluates TRUE  
26. {  
27.  Signal (write); // increase write by one, i.e. write = 1   
28. }  
29. Signal(mutex);// increase mutex by one, i.e. mutex = 1  
30.  
31. Now if again any writer wants to write, it can do it now, since write > 0  

CASE 3: WRITING -- READING → NOT ALLOWED. That is when if one process is writing into the file, then reading by another process is not allowed. Let us see that our code is working accordingly or not?

Explanation:  

1. The initial value of semaphore write = 1  
2. Suppose two processes P0 and P1 are in a system, P0 wants to write while P1 wants to read, P0 enter first into the writer code, the moment P0 enters   
3. Wait(write); will decrease semaphore write by 1, now write = 0  
4. And continue WRITE INTO THE FILE  
5. Now suppose P1 wants to read the same time (will it be allowed?) let's see.  
6. P1 enters reader's code  
7. Initial value of semaphore mutex = 1 and variable readcount = 0  
8. Wait(mutex); will decrease semaphore mutex by 1, now mutex = 0  
9. Increment readcount by 1, now readcount = 1, next  
10. If (readcount == 1)// evaluates to TRUE  
11. {  
12.  Wait (write); // since value of write is already 0, hence it   
13.                   Will enter into an infinite loop and will not be    
14.                   Allowed to proceed further (which clearly   
15.                   Proves that if one writer is writing then no    
16.                   Reader will be allowed.  
17. }  
18.  
19. The moment writer stops writing and willing to exit then   
20. This proofs that, if one process is writing, no other process is allowed to read.  
21.  
22. The moment writer stops writing and willing to exit then it will execute:  
23. Signal(write); will increase semaphore write by 1, now write = 1  
24. If now P1 wants to read it can since semaphore write > 0   

CASE 4: READING - READING → ALLOWED. That is when one process is reading the file, and other process or processes is willing to read, then they all are allowed i.e. reading - reading is not mutually exclusive. Let us see that our code is working accordingly or not?

Explanation:  

1. Initial value of semaphore mutex = 1 and variable readcount = 0  
2. Suppose three processes P0, P1 and P2 are in a system, all the three processes P0, P1, and P2 want to read, let P0 enter first into the reader code, the moment P0 enters   
3. Wait(mutex); will decrease semaphore mutex by 1, now mutex = 0  
4. Increment readcount by 1, now readcount = 1, next  
5. If (readcount == 1)// evaluates to TRUE  
6. {  
7.  Wait (write); // decrement write by 1, i.e. write = 0(which     
8.                   Clearly proves that if one or more than one   
9.                   Reader is reading then no writer will be    
10.                   Allowed.  
11. }  
12.  
13. Signal(mutex); // will increase semaphore mutex by 1, now mutex = 1 i.e. other readers are allowed to enter.  
14.  
15. And P0 continues to --READ THE FILE?  
16.  
17. →Now P1 wants to enter the reader code  
18. Current value of semaphore mutex = 1 and variable readcount = 1  
19. Let P1 enter into the reader code, the moment P1 enters   
20. Wait(mutex); will decrease semaphore mutex by 1, now mutex = 0  
21. Increment readcount by 1, now readcount = 2, next  
22. If (readcount == 1)// eval. to False, it will not enter if block  
23.  
24. Signal(mutex); // will increase semaphore mutex by 1, now mutex = 1 i.e. other readers are allowed to enter.  
25.  
26. Now P0 and P1 continues to --READ THE FILE?  
27.  
28. →Now P2 wants to enter the reader code  
29. Current value of semaphore mutex = 1 and variable readcount = 2  
30. Let P2 enter into the reader code, the moment P2 enters   
31. Wait(mutex); will decrease semaphore mutex by 1, now mutex = 0  
32. Increment readcount by 1, now readcount = 3, next  
33. If (readcount == 1)// eval. to False, it will not enter if block  
34.  
35. Signal(mutex); // will increase semaphore mutex by 1, now mutex = 1 i.e. other readers are allowed to enter.  
36.  
37. Now P0, P1, and P2 continues to --READ THE FILE?  
38.  
39.  
40. Suppose now any writer wants to enter into its code then:  
41.  
42. As the first reader P0 has executed wait (write); because of which write value is 0, therefore wait(writer); of the writer, code will go into an infinite loop and no writer will be allowed.    
43.  
44. Now suppose P0 wants to come out of system( stop reading) then  
45. Wait(mutex); //will decrease semaphore mutex by 1, now mutex = 0  
46. Readcount --; // on every exit of reader decrement readcount by   
47.                 One i.e. readcount = 2  
48.  
49. If (readcount == 0)// eval. to FALSE it will not enter if block  
50.  
51. Signal(mutex); // will increase semaphore mutex by 1, now mutex = 1 i.e. other readers are allowed to exit  
52.  
53.  
54. → Now suppose P1 wants to come out of system (stop reading) then  
55. Wait(mutex); //will decrease semaphore mutex by 1, now mutex = 0  
56. Readcount --; // on every exit of reader decrement readcount by   
57.                 One i.e. readcount = 1  
58.  
59. If (readcount == 0)// eval. to FALSE it will not enter if block  
60.  
61. Signal(mutex); // will increase semaphore mutex by 1, now mutex = 1 i.e. other readers are allowed to exit  
62.  
63. →Now suppose P2 (last process) wants to come out of system (stop reading) then  
64. Wait(mutex); //will decrease semaphore mutex by 1, now mutex = 0  
65. Readcount --; // on every exit of reader decrement readcount by   
66.                 One i.e. readcount = 0  
67.  
68. If (readcount == 0)// eval. to TRUE it will enter into if block  
69. {  
70.  Signal (write); // will increment semaphore write by one, i.e.   
71.                     Now write = 1, since P2 was the last process  
72.                     Which was reading, since now it is going out,   
73.                     So by making write = 1 it is allowing the writer      
74.                     To write now.  
75. }  
76.  
77. Signal(mutex); // will increase semaphore mutex by 1, now mutex = 1   
78.  
79.  
80. The above explanation proves that if one or more than one processes are willing to read simultaneously then they are allowed. 

Key takeaway

The readers-writers problem is used for managing synchronization among various reader and writer process so that there are no problems with the data sets, i.e. no inconsistency is generated.

3.5 Dining philosophers problem

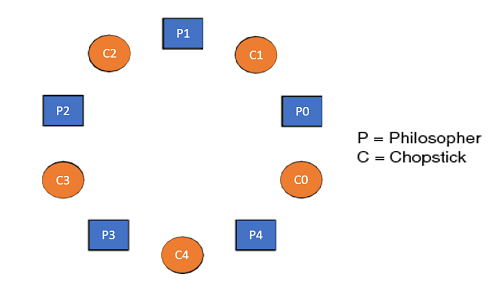
THE DINING PHILOSOPHERS PROBLEM

The dining philosopher's problem is the classical problem of synchronization which says that Five philosophers are sitting around a circular table and their job is to think and eat alternatively. A bowl of noodles is placed at the center of the table along with five chopsticks for each of the philosophers. To eat a philosopher needs both their right and a left chopstick. A philosopher can only eat if both immediate left and right chopsticks of the philosopher is available. In case if both immediate left and right chopsticks of the philosopher are not available then the philosopher puts down their (either left or right) chopstick and starts thinking again.

The dining philosopher demonstrates a large class of concurrency control problems hence it's a classic synchronization problem.

Fig 3 - Five Philosophers sitting around the table

Dining Philosophers Problem- Let's understand the Dining Philosophers Problem with the below code, we have used fig 1 as a reference to make you understand the problem exactly. The five Philosophers are represented as P0, P1, P2, P3, and P4 and five chopsticks by C0, C1, C2, C3, and C4.

1. Void Philosopher  
2. {  
3. While(1)  
4.  {  
5.   Take_chopstick[i];  
6.   Take_chopstick[ (i+1) % 5] ;  
7.   . .  
8.   . EATING THE NOODLE  
9.   .  
10.   Put_chopstick[i] );  
11.   Put_chopstick[ (i+1) % 5] ;  
12.   .  
13.   . THINKING  
14.  }  
15. }  

Let's discuss the above code:

Suppose Philosopher P0 wants to eat, it will enter in Philosopher() function, and execute take_chopstick[i]; by doing this it holds C0 chopstick after that it execute take_chopstick[ (i+1) % 5]; by doing this it holds C1 chopstick( since i =0, therefore (0 + 1) % 5 = 1)

Similarly suppose now Philosopher P1 wants to eat, it will enter in Philosopher() function, and execute take_chopstick[i]; by doing this it holds C1 chopstick after that it execute take_chopstick[ (i+1) % 5]; by doing this it holds C2 chopstick( since i =1, therefore (1 + 1) % 5 = 2)

But Practically Chopstick C1 is not available as it has already been taken by philosopher P0, hence the above code generates problems and produces race condition.

The solution of the Dining Philosophers Problem

We use a semaphore to represent a chopstick and this truly acts as a solution of the Dining Philosophers Problem. Wait and Signal operations will be used for the solution of the Dining Philosophers Problem, for picking a chopstick wait operation can be executed while for releasing a chopstick signal semaphore can be executed.

Semaphore: A semaphore is an integer variable in S, that apart from initialization is accessed by only two standard atomic operations - wait and signal, whose definitions are as follows:

1. 1. wait(S)  
2. {  
3. While( S <= 0) ;  
4. S--;  
5. }  
6.  
7. 2. signal(S)  
8. {  
9. S++;  
10. }  

From the above definitions of wait, it is clear that if the value of S <= 0 then it will enter into an infinite loop (because of the semicolon; after while loop). Whereas the job of the signal is to increment the value of S.

The structure of the chopstick is an array of a semaphore which is represented as shown below -

1. Semaphore C[5];  

Initially, each element of the semaphore C0, C1, C2, C3, and C4 are initialized to 1 as the chopsticks are on the table and not picked up by any of the philosophers.

Let's modify the above code of the Dining Philosopher Problem by using semaphore operations wait and signal, the desired code looks like

1. Void Philosopher  
2. {  
3. While(1)  
4.  {  
5.   Wait( take_chopstickC[i] );  
6.   Wait( take_chopstickC[(i+1) % 5] ) ;  
7.   . .  
8.   . EATING THE NOODLE  
9.   .  
10.   Signal( put_chopstickC[i] );  
11.   Signal( put_chopstickC[ (i+1) % 5] ) ;  
12.   .  
13.   . THINKING  
14.  }  
15. }  

In the above code, first wait operation is performed on take_chopstickC[i] and take_chopstickC [ (i+1) % 5]. This shows philosopher i have picked up the chopsticks from its left and right. The eating function is performed after that.

On completion of eating by philosopher i the, signal operation is performed on take_chopstickC[i] and take_chopstickC [ (i+1) % 5]. This shows that the philosopher i have eaten and put down both the left and right chopsticks. Finally, the philosopher starts thinking again.

Let's understand how the above code is giving a solution to the dining philosopher problem?

Let value of i = 0( initial value ), Suppose Philosopher P0 wants to eat, it will enter in Philosopher() function, and execute Wait( take_chopstickC[i] ); by doing this it holds C0 chopstick and reduces semaphore C0 to 0, after that it execute Wait( take_chopstickC[(i+1) % 5] ); by doing this it holds C1 chopstick( since i =0, therefore (0 + 1) % 5 = 1) and reduces semaphore C1 to 0

Similarly, suppose now Philosopher P1 wants to eat, it will enter in Philosopher() function, and execute Wait( take_chopstickC[i] ); by doing this it will try to hold C1 chopstick but will not be able to do that, since the value of semaphore C1 has already been set to 0 by philosopher P0, therefore it will enter into an infinite loop because of which philosopher P1 will not be able to pick chopstick C1 whereas if Philosopher P2 wants to eat, it will enter in Philosopher() function, and execute Wait( take_chopstickC[i] ); by doing this it holds C2 chopstick and reduces semaphore C2 to 0, after that, it executes Wait( take_chopstickC[(i+1) % 5] ); by doing this it holds C3 chopstick( since i =2, therefore (2 + 1) % 5 = 3) and reduces semaphore C3 to 0.

Hence the above code is providing a solution to the dining philosopher problem, A philosopher can only eat if both immediate left and right chopsticks of the philosopher are available else philosopher needs to wait. Also at one go two independent philosophers can eat simultaneously (i.e., philosopher P0 and P2, P1 and P3 & P2 and P4 can eat simultaneously as all are the independent processes and they are following the above constraint of dining philosopher problem)

The drawback of the above solution of the dining philosopher problem

From the above solution of the dining philosopher problem, we have proved that no two neighbouring philosophers can eat at the same point in time. The drawback of the above solution is that this solution can lead to a deadlock condition. This situation happens if all the philosophers pick their left chopstick at the same time, which leads to the condition of deadlock and none of the philosophers can eat.

To avoid deadlock, some of the solutions are as follows -

●        Maximum number of philosophers on the table should not be more than four, in this case, chopstick C4 will be available for philosopher P3, so P3 will start eating and after the finish of his eating procedure, he will put down his both the chopstick C3 and C4, i.e. semaphore C3 and C4 will now be incremented to 1. Now philosopher P2 which was holding chopstick C2 will also have chopstick C3 available, hence similarly, he will put down his chopstick after eating and enable other philosophers to eat.

●        A philosopher at an even position should pick the right chopstick and then the left chopstick while a philosopher at an odd position should pick the left chopstick and then the right chopstick.

●        Only in case if both the chopsticks ( left and right ) are available at the same time, only then a philosopher should be allowed to pick their chopsticks

●        All the four starting philosophers ( P0, P1, P2, and P3) should pick the left chopstick and then the right chopstick, whereas the last philosopher P4 should pick the right chopstick and then the left chopstick. This will force P4 to hold his right chopstick first since the right chopstick of P4 is C0, which is already held by philosopher P0 and its value is set to 0, i.e C0 is already 0, because of which P4 will get trapped into an infinite loop and chopstick C4 remains vacant. Hence philosopher P3 has both left C3 and right C4 chopstick available, therefore it will start eating and will put down its both chopsticks once finishes and let others eat which removes the problem of deadlock.

The design of the problem was to illustrate the challenges of avoiding deadlock, a deadlock state of a system is a state in which no progress of system is possible. Consider a proposal where each philosopher is instructed to behave as follows:

●        The philosopher is instructed to think till the left fork is available, when it is available, hold it.

●        The philosopher is instructed to think till the right fork is available, when it is available, hold it.

●        The philosopher is instructed to eat when both forks are available.

●        then, put the right fork down first

●        then, put the left fork down next

●        repeat from the beginning.

Key takeaway

The readers-writers problem is a classical problem of process synchronization, it relates to a data set such as a file that is shared between more than one process at a time. Among these various processes, some are Readers - which can only read the data set; they do not perform any updates, some are Writers - can both read and write in the data sets.

The readers-writers problem is used for managing synchronization among various reader and writer process so that there are no problems with the data sets, i.e. no inconsistency is generated.

3.6 Sleeping barber problem

Problem: The analogy is predicated upon a theoretical barber look with one barber. There's a barber look that has one barber, one chair, and n chairs for waiting for patrons if there are any to sit down on the chair.

• If there's no client, then the barber sleeps in his chair.
• When a client arrives, he has got to awaken the barber.
• If there are many purchasers and therefore the barber is cutting a customer’s hair, then the remaining customers either wait if their ar empty chairs within the {waiting room|lounge|waiting ara|room} or they leave if no chairs are empty.

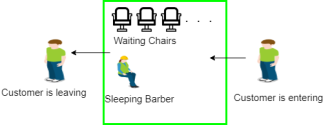
Fig 4 - Example

Solution: the answer to the current downside includes 3 semaphores. First is for the customer that counts the quantity of consumers' gift within the room (customer within the chair isn't enclosed as a result of he's not waiting). Second, the barber zero or one is employed to inform whether or not the barber is idle or is functioning, and therefore the third mutex is employed to supply the mutual exclusion that is needed for the method to execute. Within the solution, the client has the record of the quantity {of clients|of consumers|of shoppers} waiting within the room if the quantity of consumers is adequate to the number of chairs within the room then the approaching customer leaves the store.

When the barber shows up within the morning, he executes the procedure barber, inflicting him to the dam on the semaphore customers as a result of it's at the start zero. Then the barber goes to sleep till the primary client comes up.

When a client arrives, he executes the client procedure the client acquires the mutex for coming into the crucial region, if another client enters thenceforth, the other won't be able to something till the primary one has free the mutex. The client then checks the chairs within the {waiting room|lounge|waiting ara|room} if waiting customers are less then the number of chairs then he sits otherwise he leaves and releases the mutex.

If the chair is accessible then the client sits within the room and increments the variable waiting price and additionally will increase the customer’s semaphore this wakes up the barber if he's sleeping.

At now, the client and barber are each awake, and therefore the barber is prepared to relinquish that person a haircut. Once the haircut is over, the client exits the procedure, and if there aren't any customers in the room barber sleeps.

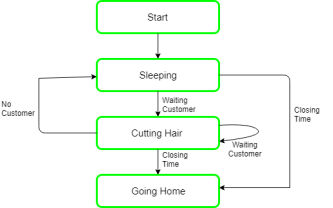
Fig 5 - Example

Algorithm for Sleeping Barber problem:

Key takeaway

Problem: The analogy is predicated upon a theoretical barber look with one barber. There's a barber look that has one barber, one chair, and n chairs for waiting for patrons if there are any to sit down on the chair.

• If there's no client, then the barber sleeps in his chair.
• When a client arrives, he has got to awaken the barber.
• If there are many purchasers and therefore the barber is cutting a customer’s hair, then the remaining customers either wait if there are empty chairs within the {waiting room|lounge|waiting ara|room} or they leave if no chairs are empty.

References:

1. Silberschatz, Galvin, Gagne, "Operating System Concepts", John Wiley and Sons, 10th edition, 2018
2. Stallings, “Operating Systems –Internals and Design Principles”, 9/E, Pearson Publications, 2018
3. Andrew S. Tanenbaum, “Modern Operating Systems”, 4/E, Pearson Publications, 2015