Unit - 1
Introduction to compiler and Finite automata
● A compiler is a translator that translates the language at the highest level into the language of the computer.
● A developer writes high-level language and the processor can understand machine language.
● The compiler is used to display a programmer's errors.
● The main objective of the compiler is to modify the code written in one language without altering the program's meaning.
● When you run a programme that is written in the language of HLL programming, it runs in two parts.
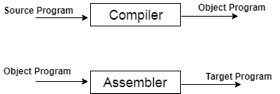
Fig 1: Execution process of Compiler
There are three phases of analysis in compiling:
1. Lexical Analysis
2. Syntax Analysis
3. Semantic Analysis
Lexical analysis
Linear analysis is referred to as lexical analysis or scanning in a compiler. The lexical analysis step examines the source program's characters and groups them into tokens, which are sequences of characters with a common meaning.
Example:
Position: = initial + rate * 60
Identifiers – position, initial, rate.
Operators - + , *
Assignment symbol - : =
Number - 60
Blanks – eliminated.
Syntax analysis
Parsing or syntax analysis are terms used to describe hierarchical analysis. It entails organizing the source program's tokens into grammatical sentences that the compiler can utilize to generate output. As seen in Fig. 1, they are represented by a syntax tree.
A syntax tree is a tree that is formed as a result of syntax analysis, with the operators on the inside and the operands on the outside.
When the syntax is incorrect, this analysis shows an error.
Example:
Position: = initial + rate * 60
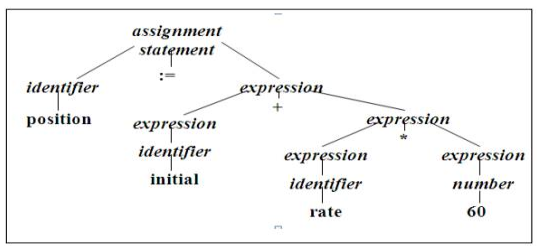
Fig 2: Parse tree for position = initial + rate*60
Semantic analysis
This step examines the source code for semantic mistakes and collects type information for the code creation phase that follows. Type checking is a crucial part of semantic analysis. The compiler verifies that each operator has operands that the source language specification allows.
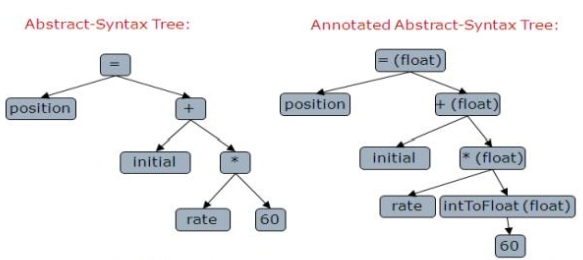
Fig 3: Semantic analysis inserts a conversion from integer to real
Key takeaway
The lexical analysis step examines the source program's characters and groups them into tokens, which are sequences of characters with a common meaning.
Type checking is a crucial part of semantic analysis.
It is said that lexemes are a character sequence (alphanumeric) in a token. For each lexeme to be identified as a valid token, there are some predefined rules. These rules, by means of a pattern, are described by grammar rules. A pattern describes what a token can be, and by means of regular expressions, these patterns are described.
Keywords, constants, identifiers, sequences, numbers, operators and punctuation symbols can be used as tokens in the programming language.
Example: the variable declaration line in the C language
Int value = 100;
Contains the tokens:
Int (keyword), value (identifiers) = (operator), 100 (constant) and; (symbol)
Patterns
A pattern is a description of the shape in which a token's lexemes can take [or match]. The pattern in the instance of a keyword as a token is just the sequence of characters that make up the term. The pattern for identifiers and some other tokens is a more complicated structure that can be matched by a large number of strings.
Lexemes
A lexeme is a sequence of characters in the source program that matches the pattern for a token and is recognized as an instance of that token by the lexical analyzer.
Example:
In the following C language statement,
Printf ("Total = %d\n‖, score);
Both printf and score are lexemes matching the pattern for token id, and "Total = %d\n‖
Is a lexeme matching literal [or string].
Description of token, patterns, and lexeme
Token | Lexeme | Pattern |
Const | Const | Const |
If | If | If |
Relation | <,<=,= ,< >,>=,> | < or <= or = or < > or >= or letter followed by letters & digit |
i | Pi | Any numeric constant |
Nun | 3.14 | Any character b/w “and “except" |
Literal | "core" | Pattern |
Key takeaway
It is said that lexemes are a character sequence (alphanumeric) in a token. For each lexeme to be identified as a valid token, there are some predefined rules. These rules, by means of a pattern, are described by grammar rules. A pattern describes what a token can be, and by means of regular expressions.
The method of compilation includes the sequence of different stages. Each phase takes a source programme in one representation and produces output in another representation. From its previous stage, each process takes input.
The various stages of the compiler take place:
- Lexical Analysis
- Syntax Analysis
- Semantic Analysis
- Intermediate Code Generation
- Code Optimization
- Code Generation
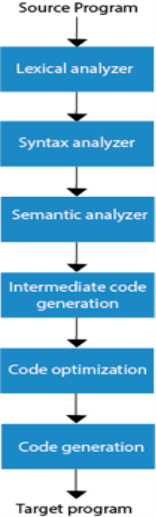
Fig 4: Phases of compiler
- Lexical Analysis: The first phase of the compilation process is the lexical analyzer phase. As input, it takes source code. One character at a time, it reads the source programme and translates it into meaningful lexemes. These lexemes are interpreted in the form of tokens by the Lexical analyzer.
- Syntax Analysis: Syntax analysis is the second step of the method of compilation. Tokens are required as input and a parse tree is generated as output. The parser verifies that the expression made by the tokens is syntactically right or not in the syntax analysis process.
- Semantic Analysis: The third step of the method of compilation is semantic analysis. This tests whether the parse tree complies with language rules. The semantic analyzer keeps track of identifiers, forms, and expressions of identifiers. The output step of semantic analysis is the syntax of the annotated tree.
- Intermediate Code Generation: The compiler generates the source code into an intermediate code during the intermediate code generation process. Between high-level language and machine language, intermediate code is created. You can produce the intermediate code in such a way that you can convert it easily into the code of the target computer.
- Code Optimization: An optional step is code optimization. It is used to enhance the intermediate code so that the program's output can run quicker and take up less space. It eliminates redundant code lines and arranges the sequence of statements to speed up the execution of the programme.
- Code Generation: The final stage of the compilation process is code generation. It takes as its input the optimised intermediate code and maps it to the language of the target computer. The code generator converts the intermediate code to the required computer's machine code.
Key takeaway
The method of compilation includes the sequence of different stages. Each phase takes a source programme in one representation and produces output in another representation. From its previous stage, each process takes input.
A parser is a compiler that is used to break down data from the lexical analysis step into smaller pieces.
A parser is a program that takes a sequence of tokens as input and creates a parse tree as output.
There are two forms of parsing: top down and bottom up.
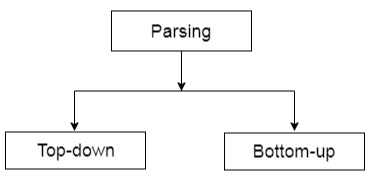
Fig 5: Types of parsing
Key takeaway
A parser is a compiler that is used to break down data from the lexical analysis step into smaller pieces.
● The graphical representation of symbols is the Parse tree. Terminal or non-terminal may be the symbol.
● In parsing, using the start symbol, the string is derived. The starter symbol is the root of the parse tree.
● It is the symbol's graphical representation, which can be terminals or non-terminals.
● The parse tree follows operators' precedence. The deepest sub-tree went through first. So, the operator has less precedence over the operator in the sub-tree in the parent node.
Following these points, the parse tree:
● The terminals have to be all leaf nodes.
● Non-terminals have to be all interior nodes.
● In-order traversal supplies the initial string of inputs.
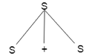
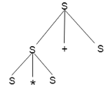
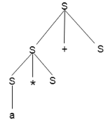
Example
Production rules:
- T= T + T | T * T
- T = a|b|c
Input
a * b + c
Step 1:
Step 2:
Step 3:
Step 4:
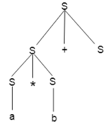
Step 5:
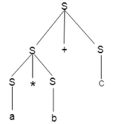
Key takeaway
The graphical representation of symbols is the Parse tree. Terminal or non-terminal may be the symbol.
In parsing, using the start symbol, the string is derived. The starter symbol is the root of the parse tree.
If there is more than one leftmost derivation or more than one rightmost derivative or more than one parse tree for the given input string, grammar is said to be ambiguous. It's called unambiguous if the grammar is not vague.
Example:
- S = aSb | SS
- S = ∈
The above grammar produces two parse trees for the string Aabb:
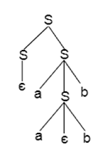
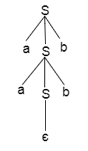
If there is uncertainty in the grammar, then it is not good for constructing a compiler.
No method can detect and remove ambiguity automatically, but by re-writing the entire grammar without ambiguity, you can remove ambiguity.
Key takeaway:
If there is more than one left or right most derivation or more than one parse tree for the given input string, grammar is said to be ambiguous.
Precedence and associativity are two operator qualities that determine how operands are grouped with operators. When grouping various types of operators with their operands, precedence takes precedence. The left-to-right or right-to-left order for grouping operands to operators with the same precedence is known as associativity. The precedence of an operator is only relevant if other operators with higher or lower precedence are present. Higher-precedence operators are evaluated first in expressions. Parentheses can be used to compel the grouping of operands.
Because of the right-to-left associativity of the = operator, the value of 5 is assigned to both a and b in the following expressions. After that, the value of c is allocated to b, and then b is assigned to a.
b = 9;
c = 5;
a = b = c;
Because the order in which subexpressions are evaluated is not determined, you can use parentheses to compel the grouping of operands with operators.
In this phrase,
a + b * c / d
Because of their priority, the * and / operations are executed before +. Because of associativity, b is multiplied by c before being divided by d.
The tables below illustrate the order of precedence for the C and C++ language operators, as well as the direction of associativity for each operator. The precedence of operators of the same rank is the same.
Recursive or predictive parsing is known as top-down parsing.
The parsing begins with the start symbol in the top-down parsing and transforms it into the input symbol.
The top-down parser is the parser that, by expanding the non-terminals, generates a parse for the given input string with the aid of grammar productions, i.e. it begins from the start symbol and ends on the terminals.
Parse Tree The input string representation of acdb is as follows:
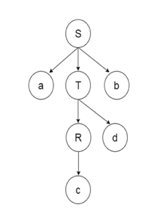
Fig 6: Parse tree
There are 2 types of additional Top-down parser: Recursive descent parser, and Non-recursive descent parser.
- Recursive descent parser:
It is also known as Brute force parser or the with backtracking parser. Basically, by using brute force and backtracking, it produces the parse tree.
A top-down parsing technique that builds the parse tree from the top and reads the input from left to right is recursive descent. For any terminal and non-terminal entity, it uses procedures.
The input is recursively parsed by this parsing technique to make a parse tree, which may or may not require back-tracking. But the related grammar (if not left-faced) does not prevent back-tracking. Predictive is considered a type of recursive-descent parsing that does not require any back-tracking.
As it uses context-free grammar that is recursive in nature, this parsing technique is called recursive.
2. Non-recursive descent parser:
It is also known with or without a backtracking parser or dynamic parser, LL(1) parser or predictive parser. It uses the parsing table instead of backtracking to create the parsing tree.
Key takeaway
The top-down parser is the parser that, by expanding the non-terminals, generates a parse for the given input string with the aid of grammar productions, i.e. it begins from the start symbol and ends on the terminals.
Bottom up parsing is also known as parsing for shift-reduce.
Bottom-up parsing is used to build an input string parsing tree.
The parsing begins with the input symbol in the bottom up parsing and builds the parse tree up to the start symbol by tracing the rightmost string derivations in reverse.
Parsing from the bottom up is known as multiple parsing.
Shift reduce parsing
● Shift reduction parsing is a mechanism by which a string is reduced to the beginning symbol of a grammar.
● Using a stack to hold the grammar and an input tape to hold the string, Shift reduces parsing.
● The two acts are done by Shift Decrease Parsing: move and decrease. This is why it is considered that shift reduces parsing.
● The current symbol in the input string is moved into the stack for the shift operation.
● The symbols will be substituted by the non-terminals at each reduction. The mark is the right side of manufacturing and the left side of output is non-terminal.
Example:
Grammar:
- S → S+S
- S → S-S
- S → (S)
- S → a
Input string:
a1-(a2+a3)
Parsing table:
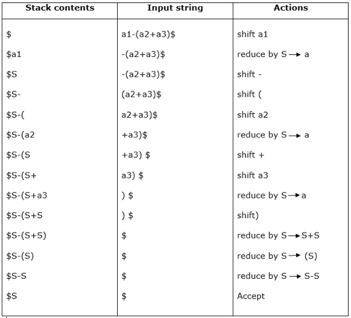
For bottom-up parsing, shift-reduce parsing uses two special steps. Such steps are referred to as shift-step and reduce-step.
Shift - step: The shift step refers to the progression to the next input symbol, which is called the shifted symbol, of the input pointer. Into the stack, this symbol is moved. The shifted symbol will be viewed as a single parse tree node.
Reduce - step: When a complete grammar rule (RHS) is found by the parser and substituted with (LHS), it is known as a reduction stage.This happens when a handle is located at the top of the stack. A POP function is performed on the stack that pops off the handle and substitutes it with a non-terminal LHS symbol to decrease.
Key takeaway:
- Bottom up parsing is also known as parsing for shift-reduce.
- Bottom-up parsing is used to build an input string parsing tree.
- Shift reduction parsing is a mechanism by which a string is reduced to the beginning symbol of a grammar.
If the RHS's leftmost variable is the same as the LHS's variable, a grammatical production is said to have left recursion.
Left Recursive Grammar is a grammar that contains a production with left recursion.
Example
For Top down parsers, left recursion is seen as a difficult scenario.
As a result, left recursion must be removed from the grammar.
Elimination of left recursions
Left recursion is eliminated by converting the grammar into a right recursive grammar.
If we have the left-recursive pair of productions-
A → Aα / β
(Left Recursive Grammar)
Where β does not begin with an A.
Then, we can eliminate left recursion by replacing the pair of productions with-
A → βA’
A’ → αA’ / ∈
(Right Recursive Grammar)
This right recursive grammar functions same as left recursive grammar.
We correlate some informal notations with the grammar in syntax directed translation, and these notations are referred to as semantic rules.
So we can conclude that
Grammar + semantic rule = SDT (syntax directed translation)
● Depending on the type of attribute, every non-terminal can get one, more than one, or even 0 attributes in syntax directed translation. The semantic rules linked with the production rule evaluate the value of these properties.
● A string, a number, a memory address, or a complicated record can all be stored in an attribute, according to the semantic rule.
● When a construct is encountered in a programming language, it is translated according to the semantic rules defined in that programming language.
Production | Semantic Rules |
E → E + T | E.val := E.val + T.val |
E → T | E.val := T.val |
T → T * F | T.val := T.val + F.val |
T → F | T.val := F.val |
F → (F) | F.val := F.val |
F → num | F.val := num.lexval |
One of E's properties is E.val.
The lexical analyzer returns the attribute num.lexval.
The Chomsky Hierarchy describes the class of languages that the various machines embrace. The language group in Chomsky's Hierarchy is as follows:
Grammar Type | Grammar Accepted | Language Accepted | Automaton |
Type 0 | Unrestricted grammar | Recursively enumerable language | Turing Machine |
Type 1 | Context-sensitive grammar | Context-sensitive language | Linear-bounded automaton |
Type 2 | Context-free grammar | Context-free language | Pushdown automaton |
Type 3 | Regular grammar | Regular language | Finite state automaton |
- Type 0 known as Unrestricted Grammar.
- Type 1 known as Context Sensitive Grammar.
- Type 2 known as Context Free Grammar.
- Type 3 Regular Grammar.
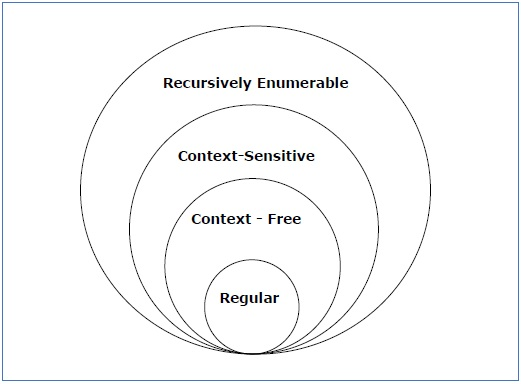
Fig 7: Types of grammar
The above diagram shows the classification of chomsky. Each language of type 3 is therefore also of type 2, 1 and 0 respectively. Similarly, every language of type 2 is also of type 1 and type 0 likewise.
● Type 0 grammar -
Type 0 grammar is known as Unrestricted grammar. The grammar rules of these types of languages are unregulated. Turing machines can model these languages efficiently.
Example:
- BAa → aa
- P → p
● Type 1 grammar -
Type 1 grammar is known as Context Sensitive Grammar. Context-sensitive grammar is used to describe language that is sensitive to context. The context-sensitive grammar follows the rules below:
● There may be more than one symbol on the left side of their development rules for context-sensitive grammar.
● The number of left-hand symbols does not surpass the number of right-hand symbols.
● The A → ε type rule is not permitted unless A is a beginning symbol. It does not occur on the right-hand side of any rule.
● The Type 1 grammar should be Type 0. Production is in the form of V →T in type1
Key takeaway:
● Where the number of symbols in V is equal to or less than T
Example:
- S → AT
- T → xy
- A → a
● Type 2 grammar -
Type 2 Grammar is called Context Free Grammar. Context free languages are the languages which can be represented by the CNF (context free grammar) Type 2 should be type 1. The production rule is:
A → α
Key takeaway:
● Where A is any single non-terminal and is any combination of terminals and non-terminals.
Example:
- A → aBb
- A → b
- B → a
● Type 3 grammar -
Type 3 Grammar is called Regular Grammar. Those languages that can be represented using regular expressions are regular languages. These languages may be NFA or DFA-modelled.
Type3 has to be in the form of -
V → T*V / T*
Example:
A → xy
Key takeaway:
● The most limited form of grammar is Type3. Type2 and Type1 should be the grammar of Type3.
NDFA applies to Finite Non-Deterministic Automata. It is used for a single input to pass through any number of states. NDFA embraces the NULL step, indicating that without reading the symbols, it can change the state.
Like the DFA, NDFA also has five states. NDFA, however, has distinct transformation features.
NDFA's transition role may be described as:
δ: Q x ∑ →2Q
Graphical Representation of NFA
An NFA can be represented by digraphs called state diagram. In which:
- The state is represented by vertices.
- The arc labeled with an input character show the transitions.
- The initial state is marked with an arrow.
- The final state is denoted by the double circle.
Example
- Q = {q0, q1, q2}
- ∑ = {0, 1}
- q0 = {q0}
- F = {q2}
Solution:
Transition Diagram:
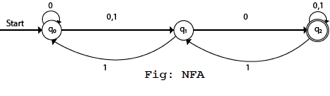
Transition table:
Present State | Next State for Input 0 | Next State of Input 1 |
→q0 | q0, q1 | q1 |
q1 | q2 | q0 |
*q2 | q2 | q1, q2 |
In this figure, we can see that the current state is q0 (input 0), and the next state will be q0, q1 (input 1) so the next state is q1. When the current state is q1 (input 0), the next state will be q2 (input 1), the next state is q0. When the current state is q2 (input 0), the next state is q2 (input 1), the next state will be q1 or q2.
Key takeaway:
● To identify patterns, finite state machines are used.
● FA has two states: state approve or state deny.
● In DFA, the character of the input goes to only one state.
DFA stands for Deterministic Finite Automata. Deterministic refers to computational uniqueness. In DFA, the character of the input goes to only one state. The DFA does not allow the null shift, which means that without an input character, the DFA does not change the state.
DFA has five tuples {Q, ∑, q0, F, δ}
Q: set of all states
∑: finite set of input symbol where δ: Q x ∑ →Q
q0: initial state
F: final state
δ: Transition function
Representation
A DFA can be represented by digraphs called state diagram. In which:
- The state is represented by vertices.
- The arc labeled with an input character shows the transitions.
- The initial state is marked with an arrow.
- The final state is denoted by a double circle.
Advantages and disadvantages
● DFAs are used to model a Turing machine.
● They are used as++ models of computation.
● The union/intersection of the languages recognized by two given DFAs.
● The complement of the language recognized by a given DFA.
Example
- Q = {q0, q1, q2}
- ∑ = {0,1}
- q0 = {q0}
- F = {q2}
Solution:
Transition Diagram:

Transition Table:
Present State | Next State for Input 0 | Next state of Input 1 |
→q0 | q0 | q1 |
q1 | q2 | q1 |
*q2 | q2 | q2 |
Let X = (Qx, ∑, δx, q0, Fx) be an NFA which accepts the language L(X). We have to design an equivalent DFA Y = (Qy, ∑, δy, q0, Fy) such that L(Y) = L(X). The following procedure converts the NFA to its equivalent DFA −
Algorithm
Input − An NFA
Output − An equivalent DFA
Step 1: Create a state table using the NDFA provided.
Step 2: Create a blank state table for the comparable DFA under possible input alphabets.
Step 3: Use q0 to mark the DFA's start state (Same as the NDFA).
Step 4: For each possible input alphabet, get the combination of States Q0, Q1,..., Qn.
Step 5: We must repeat step 4 each time we construct a new DFA state under the input alphabet columns; otherwise, proceed to step 6.
Step 6: The states that contain any of the NDFA's final states are the analogous DFA's final states.
Example
Take a look at the NFA in the diagram below.
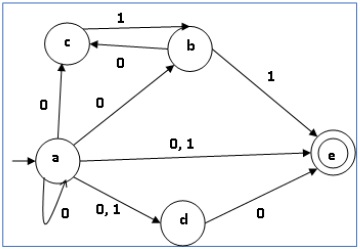
q | δ(q,0) | δ(q,1) |
a | {a,b,c,d,e} | {d,e} |
b | {c} | {e} |
c | ∅ | {b} |
d | {e} | ∅ |
e | ∅ | ∅ |
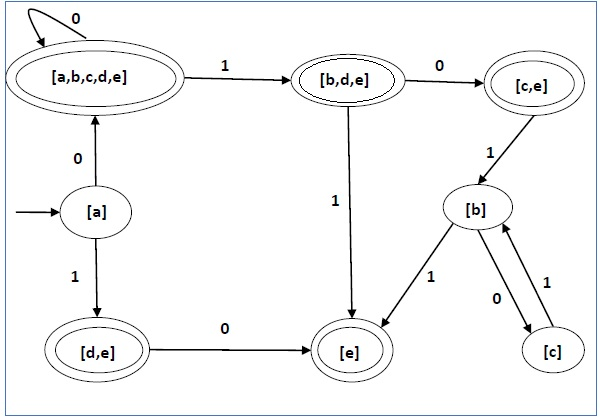
We find its corresponding DFA using the approach described above. The DFA's state table can be found below.
q | δ(q,0) | δ(q,1) |
[a] | [a,b,c,d,e] | [d,e] |
[a,b,c,d,e] | [a,b,c,d,e] | [b,d,e] |
[d,e] | [e] | ∅ |
[b,d,e] | [c,e] | [e] |
[e] | ∅ | ∅ |
[c, e] | ∅ | [b] |
[b] | [c] | [e] |
[c] | ∅ | [b] |
The DFA's state diagram is as follows:
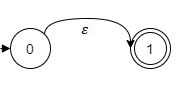
As a foundation for the building, we'll employ the rules that define a regular expression:
- The empty string is represented by the NFA:
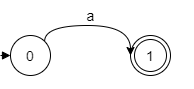
2. If the regular expression is just a single character, such as a, the NFA is:
3. The union operator is represented by a selection of node transitions; hence, a|b can be written as:
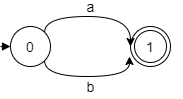
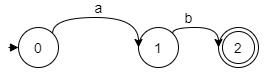
4. Concatenation is merely the process of joining two NFAs together; for example, ab is:
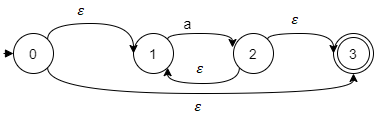
5. The Kleene closure must allow zero or more instances of the letter to be taken from the input; consequently, a* looks like:
Three Methods to Optimize
● Directly build DFA from regular expression.
● Minimize states
● Compact transition tables
Constructing Direct DFA
● We begin by concatenating the specified regular expression with the special symbol #.
● The regular expression r will be (r)# enhanced.
● Second, with this modified regular expression, we generate a syntax tree.
● All alphabet symbols (excluding # and the empty string) in the expanded regular expression will be on the leaves of this syntax tree.
● In the augmented regular expression, all inner nodes will be operators.
Example

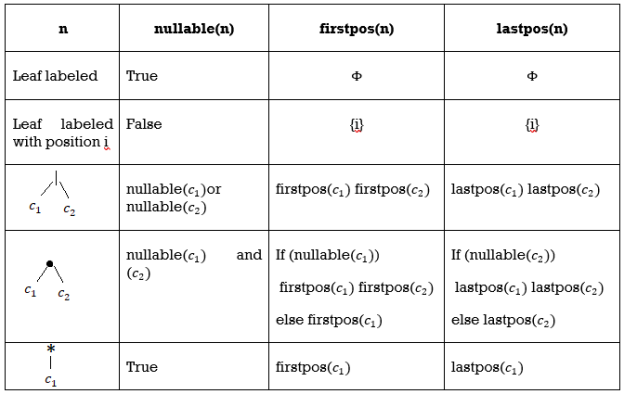
Followpos - The collection of places that can follow the position I in the strings created by the augmented regular expression is called followpos(i).

Firstpos - firstpos(n) is the set of first symbol positions in strings generated by a subexpression rooted by n.
Lastpos - lastpos(n) is the set of positions of the final symbols of strings created by the n-rooted subexpression.
Calculating Firstpos and Lastpos & nullable
Evaluating Followpos
All positions in firstpos(c2) are in followpos if n is a concatenation-node with left child c1 and right child c2, and I is a position in lastpos(c1) (i).
All positions in firstpos(n) are in followpos(n) if n is a star-node and I is a position in lastpos(n) (i).

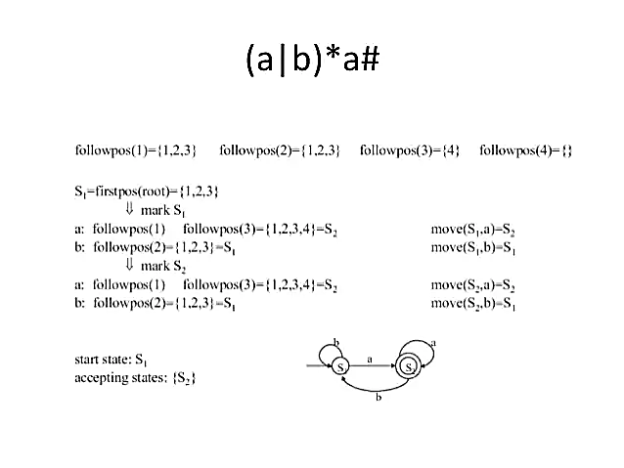
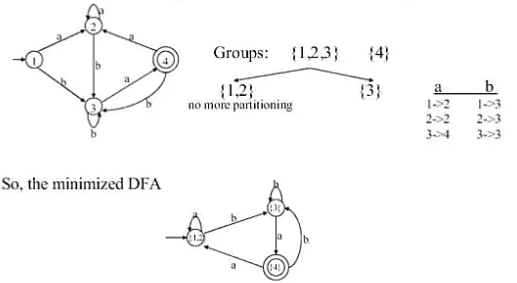
Minimizing number of states of DFA
Divide the states into two categories:
● G 1 is a collection of acceptable states.
● G2: a collection of states that aren't acceptable.
For each new group G, divide G into subgroups so that states s1 and s2 are in the same group if states s1 and s2 have transitions to states in the same group for all input symbols a.
The group holding the original DFA's start state is the start state of the minimized DFA.
The groups comprising the accepting states of the original DFA are the accepting states of the simplified DFA.
Example
Compacting Transition Tables
● A DFA two-dimensional table indexed by states and characters has a transition function.
● A typical lexical analyzer includes hundreds of states and a 128-character ASCII alphabet.
● Compilers "live" on small devices, therefore 1 MB may be insufficient.
Alternate Representations
The following is a list of character-state pairs.
a default state at the conclusion 1. Any input character that isn't on the list is chosen. 2. The following state that occurs the most frequently.
As a result, the table is drastically decreased.
References:
- Alfred V. Aho, Ravi Sethi, Jeffrey D. Ullman, Monica S. Lam, Compilers: Principles, Techniques, and Tools. Addison‐Wesley, 2006 (optional).
- Compiler design in C, A.C. Holub, PHI.
- Compiler construction (Theory and Practice), A.Barret William and R.M. Bates, Galgotia Publication.
- Https://www.slideshare.net/kiranacharya520/optimization-of-dfa
- Http://www.cs.may.ie/staff/jpower/Courses/Previous/parsing/node5.html