Unit - 2

Context Free Grammar

2.1 RE vs. CFG

The difference between RE and CFG

2.2 Eliminating ambiguity and left recursion

Suppose we have a context free grammar G with production rules:

S->aSb|bSa|SS|ɛ

Left most derivation (LMD) and Derivation Tree:

Leftmost derivation of a string from staring symbol S is done by replacing leftmost

Non-terminal symbol by RHS of corresponding production rule.

For example:

The leftmost derivation of string abab from grammar G above is done as:

S =>aSb =>abSab =>abab

The symbols in bold are replaced using production rules.

Derivation tree: It explains how string is derived using production rules from S and

Is shown in Figure.

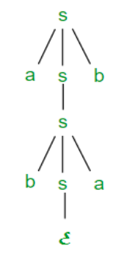
Fig 1: Derivation tree

Right most derivation (RMD):

It is done by replacing rightmost non-terminal symbol S by RHS of corresponding production rule.

For Example: The rightmost derivation of string abab from grammar G above

Is done as:

S =>SS =>SaSb =>Sab =>aSbab =>abab

The symbols in bold are replaced using production rules.

The derivation tree for abab using rightmost derivation is shown in Figure.

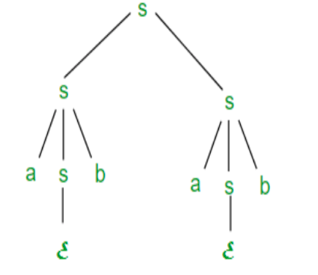
Fig 2: Right most derivation

A derivation can be either LMD or RMD or both or none.

For Example:

S =>aSb =>abSab =>abab is LMD as well as RMD But

S => SS =>SaSb =>Sab =>aSbab =>abab is RMD but not LMD.

Ambiguous Context Free Grammar:

●      A context free grammar is called ambiguous if there exists more than one

LMD or RMD for a string which is generated by grammar.

●      There will also be more than one derivation tree for a string in ambiguous grammar.

●      The grammar described above is ambiguous because there are two derivation Trees.

●      There can be more than one RMD for string abab which are:

S =>SS =>SaSb =>Sab =>aSbab =>abab

S =>aSb =>abSab =>abab

Left recursion

Any non-terminal 'A' whose derivation contains 'A' itself as the left-most symbol makes a grammar left-recursive. For top-down parsers, left-recursive grammar is seen as a difficult scenario. Top-down parsers begin parsing with the Start symbol, which is non-terminal in and of itself. As a result, when the parser encounters the same non-terminal multiple times during its derivation, it becomes difficult for it to determine when to cease parsing the left non-terminal, and it enters an infinite loop.

Example

(1) A => Aα | β

(2) S => Aα | β

A => Sd

(1) is an example of immediate left recursion, where A represents a string of non-terminals and represents any non-terminal symbol.

(2) is an indirect-left recursion example.

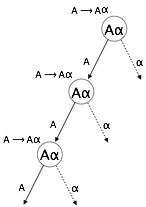
A top-down parser will first parse the A, which will result in a string containing solely of A, and the parser may repeat indefinitely.

Removal of left recursion

The following technique can be used to remove left recursion:

The show's production

A => Aα | β

Is transformed into the following products

A => βA'

A'=> αA' | ε

The strings obtained from the grammar are unaffected, but immediate left recursion is removed.

The following procedure, which should eliminate all direct and indirect left recursions, is the second method.

START

Arrange non-terminals in some order like A1, A2, A3,…, An

For each i from 1 to n

{

For each j from 1 to i-1

{

Replace each production of form Ai ⟹Aj𝜸

With Ai ⟹ δ1𝜸  | δ2𝜸 | δ3𝜸 |…| 𝜸

Where Aj ⟹ δ1 | δ2|…| δn  are current Aj productions

}

}

Eliminate immediate left-recursion

END

Key takeaway:

If there is uncertainty in the grammar, then it is not good for the construction of compilers.

No method can detect and eliminate ambiguity automatically, but by re-writing the entire grammar without ambiguity, we can remove ambiguity.

2.3 Left factoring

If a common prefix string exists in more than one grammar production rule, the top-down parser is unable to choose which of the production rules to use to parse the string at hand.

Example

When a top-down parser comes across a production like this,

A ⟹ αβ | α𝜸 | …

Because both productions start from the same terminal, it can't decide which one to use to parse the string (or non-terminal). We utilize a method known as left factoring to clear out the ambiguity.

Left factoring modifies the grammar so that top-down parsers can use it. In this method, we build one production for each common prefix and then add more productions to complete the derivation.

Example

The productions listed above can be written in a variety of ways.

A => αA'

A'=> β | 𝜸 | …

The parser now only has one production per prefix, making decision-making easier.

Key takeaway

If a common prefix string exists in more than one grammar production rule, the top-down parser is unable to choose which of the production rules to use to parse the string at hand.

References:

1. Alfred V. Aho, Ravi Sethi, Jeffrey D. Ullman, Monica S. Lam, Compilers: Principles, Techniques, and Tools. Addison‐Wesley, 2006 (optional).
2. Compiler construction (Theory and Practice), A.Barrett William and R.M. Bates, Galgotia Publication.
3. Compiler Design, Kakde.
4. Https://www.tutorialspoint.com/compiler_design/compiler_design_syntax_analysis.htm