Unit - 3

Compiler Parser

3.1 Top down parsing - LL parser, LL grammars

It is also known with or without a backtracking parser or dynamic parser, LL(1) parser or predictive parser. It uses the parsing table instead of backtracking to create the parsing tree.

Predictive parser is a recursive descent parser, which has the capability to predict which production is to be used to replace the input string. The predictive parser does not suffer from backtracking.

To accomplish its tasks, the predictive parser uses a look-ahead pointer, which points to the next input symbols. To make the parser back-tracking free, the predictive parser puts some constraints on the grammar and accepts only a class of grammar known as LL(k) grammar.

Predictive parsing uses a stack and a parsing table to parse the input and generate a parse tree. Both the stack and the input contains an end symbol $ to denote that the stack is empty and the input is consumed. To make some decision on the input and stack element combination, the parser refers to the parsing table.

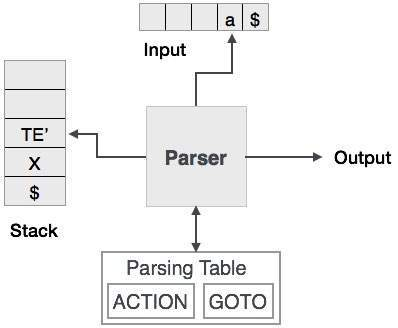
Fig 1: Predictive parser

In recursive descent parsing, for a single instance of input, the parser can have more than one output to choose from, while in predictive parser, each stage has at most one production to choose from. There may be instances where the input string does not fit the production, making the parsing procedure fail.

LL grammar

An LL grammar, in formal language theory, is a context-free grammar that may be analyzed by an LL parser, which parses the input from left to right and builds the sentence's Leftmost derivation (hence LL, compared with LR parser that constructs a rightmost derivation). An LL language is a language that has an LL grammar. Deterministic context-free grammars (DCFGs) and deterministic context-free languages (DCFLs) are subsets of each other. To show that a grammar or language belongs to this class, one might say "is an LL grammar/language" or simply "is LL."

LL parsers, like LR parsers, are table-based parsers. LL grammars can also be defined as those that can be parsed by a predictive parser (a recursive descent parser without backtracking) and can be created by hand. The formal features of LL grammars are discussed in this article; for parsing, see LL parser or recursive descent parser.

Applications

Many computer languages[clarify] are designed to be LL(1) for this reason. LL grammars, particularly LL(1) grammars, are of great practical interest because they are straightforward to parse, either by LL parsers or by recursive descent parsers. Languages based on grammars with a large k value have traditionally been thought to be difficult to parse, however this is no longer the case, thanks to the availability and widespread use of parser generators that support LL(k) grammars for any k.

Key takeaway:

1. A top-down parsing technique that builds the parse tree from the top and reads the input from left to right is recursive descent.
2. The input is recursively parsed by this parsing technique to make a parse tree, which may or may not require back-tracking.
3. Predictive parser is a recursive descent parser, which has the capability to predict which production is to be used to replace the input string

3.2 Bottom up parsing - LR parser, SLR parser, CLR parser, LALR Parser

LR parser

●      In the LR parser, “L” means left to right scanning of any input.

●      One form of bottom up parsing is LR parsing. It is used to evaluate a broad grammar class.

●      R" stands for the construction of a proper reverse derivation.

●      "K" is the number of look-ahead input symbols used to make a number of parsing decisions.

LR parsing is divided into four parts: parsing for LR (0), parsing for SLR, parsing for CLR and parsing for LALR.

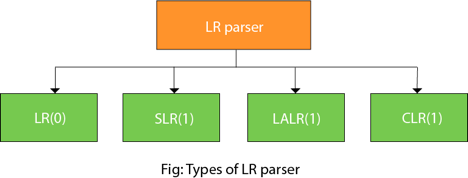
Fig 2: Types of LR parser

LR algorithm:

The stack, input, output and parsing table are required by the LR algorithm. The input, output and stack are the same in all modes of LR parsing, but the parsing table is different.

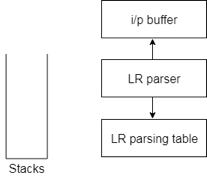
Fig 3: Diagram of LR parser

●      The input buffer is used to denote the end of the input and includes the string followed by the $ symbol to be parsed.

●      To contain a series of grammar symbols with $ at the bottom of the stack, a stack is used.

●      A two dimensional array is a parsing table. It comprises two parts: Action part and Go To part.

LR (1) parser:

Different steps involved in LR (1) Parsing:

●      Write context-free grammar for the specified input string.

●      Verify the grammar's uncertainty.

●      Add the Augmentation output to the specified grammar.

●      Creating a canonical set of objects from LR (0).

●      Drawing a diagram of data flow (DFA).

●      Build a table for LR (1) parsing.

Augment Grammar:

If we add one more output to the given grammar G, Augmented Grammar G will be generated. It allows the parser to define when the parsing should be stopped and to announce the acceptance of the input.

Example

Given grammar

S → AA 

A → aA | b 

The Augment grammar G is represented by

1. S→ S 
2. S → AA 
3. A → aA | b

Key takeaway:

●      The current symbol in the input string is moved into the stack for the shift operation.

●      The shifted symbol will be viewed as a single parse tree node.

●      LR(1) parser Verify the grammar's uncertainty.

●      In the LR parser, “ L” means left to right scanning of any input .

●      The stack, input, output and parsing table are required by the LR algorithm.

SLR parser

​​SLR (1) refers to fast parsing of LR. It's the same as parsing for LR(0). The only difference is in the parsing table. We use canonical LR (0) item array to create the SLR (1) parsing table.

We just position the reduction step in the follow-up of the left hand side in the SLR (1) parsing.

Different steps related to SLR (1) Parsing:

●      Write a context free grammar for the specified input string

●      Verify the grammar's uncertainty

●      Add Increase output in the grammar specified

●      Build a canonical set of things from LR (0)

●      Drawing a diagram of data flow (DFA)

●      Build an SLR (1) table for parsing

SLR(1) Table Construction :

Start at rule zero for the rules in an augmented grammar, G ', and follow the steps below:

Steps of State Formation (big picture algorithm)

1. Apply the Start and Start operations

2. Attain the State:

1. Using one reading operation in the current state on item C (non-terminal or terminal) form more states.
2. Apply the whole procedure to the new nations.
3. Repeat steps a and b until it is possible to form no more new states.

Example:

Consider the augmented grammar G'

S’ ‐‐>  S$

S  ‐‐>  aSbS

S  ‐‐>  a

The set of Item Sets LR(0), states:

I0     [S’ -> .S$]  (Operation to start; read on S goes to I11 (state 1)  )

[S -> .aSbS] (Full S rule operation; the reading on 'a' goes to I2 (state 2) )

[S -> .a] (For all rules 'S', continue to complete; read on 'a', to state 2 )

I1      [S’ -> S.$] (From the first line, read on 'S'; Note: never read on '$'

Nothing to read about; nothing to end )

I2      [S -> a.SbS] (Reading from state I0 on 'a'; reading on'S 'goes to I3 (state 3) )

[S -> a.]  (Continue reading on 'a' from state I0 (see stage 2 of formation of state)   with nothing to read on; nothing to complete )

[S -> .aSbS] (Complete the state in the first item read on 'a' cycles back to state 2  because of '.S' )

[S -> .a] (All grammar rules for 'S' ditto read on 'a' cycles remain full back to state 2 )

I3       [S -> aS.bS] (The dot is before a non-terminal from the reading on'S 'from state I2,   no full operation read on' b 'goes to I4 (state 4) )

I4 [S -> aSb.S] (From reading from state I3 on 'b'; reading from'S 'goes to I5 (state 5) )

[S -> .aSbS] (Due to the '.S' in the first object, complete the state;

Note: always dot in front for complete points

Return to State 2 read on 'a' cycles )

[S -> .a] ( Continue complete; ditto read back to state 2 on 'a' cycles )

I5  [S -> aSbS.] (From state 5 to read on 'S'; nothing to read on )

Construct the parse table:

You need the FIRST and FOLLOW sets for each non-terminal in your grammar to construct the parsing table.

You will need the completed collection of products for the state from above.

Now, for your parse table, draw the n x m table and mark it appropriately. The n is equal to the number of states from part 1 that you have. By counting all non-terminals and all terminals in the grammar, you decide the M. Provide a row or column for each element of n and m.

Label each row n, starting at zero, with a state number. Mark each column m, beginning from left to right, with one terminal per column. Labeling the remaining columns after labelling with all the terminals

With those non-terminals.

The ACTION side is the group of columns on the left (terminals). The group of columns is the GOTO side on the right (non-terminals)

You obey these four rules to fill out the table,

Construction rules

α, β = any string of terminals and/or non‐terminals

X, S’, S = non‐terminals

(When dot is in middle)

1. If [A ‐‐> α.aβ] ε Ii and read on ‘a’ produces Ij then ACTION [i , a] = SHIFT j.

2. If [A ‐‐> α.Xβ] ε Ii and read on ‘X’ produces Ij then GOTO [i , X] = j.

(When dot is at end)

3. If [A ‐‐> α.] ε Ii then ACTION [i , a] = REDUCE on A ‐> α for all a ε FOLLOW(A).

4. If [S’ ‐‐> S.] ε Ii then ACTION [i , $] = ACCEPT.

For example, the parsing table:

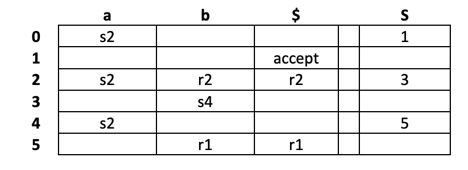
Key takeaway:

●      SLR (1) refers to fast parsing of LR.

●      It's the same as parsing for LR(0).

CLR parser

●      Canonical lookahead is referred to by CLR. To create the CLR (1) parsing table, CLR parsing utilises the canonical set of LR (1) objects. As compared to the SLR (1) parsing, the CLR (1) parsing table produces a greater number of states.

●      We only position the reduction node in the lookahead symbols in the CLR (1).

●      Different steps used in CLR (1) Parsing:

●      Write a context free grammar for the specified input string

●      Verify the grammar's uncertainty

●      Add Increase output in the grammar specified

●      Build a canonical set of things from LR (0)

●      Drawing a diagram of data flow (DFA)

●      Build a CLR (1) table for parsing

LR (1) item

Item LR(1) is a list of things from LR(0) and a look-ahead sign.

LR (1) item = LR (0) item + look ahead

The look ahead is used to decide where the final item will be put.

For the development of claims, the look ahead often adds the $ symbol.

Example

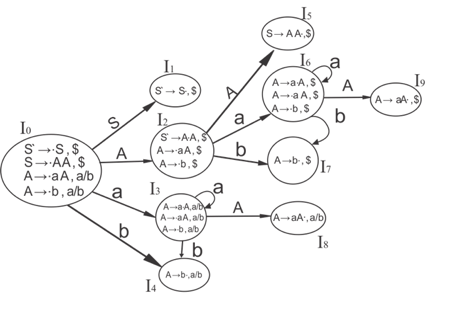
CLR ( 1 ) Grammar

1. S → AA 
2. A → aA 
3. A → b 

Add Augment Production, insert the symbol '•' for each production in G at the first position and add the lookahead as well.

1. S → •S, $ 
2. S  → •AA, $ 
3. A  → •aA, a/b  
4. A → •b, a/b

I0 state:

Add the output of Augment to the I0 State and compute the closure

I0 = Closure (S → •S)

In changed I0 State, add all productions beginning with S since "." is followed by the non-terminal. So, it will become the I0 State.

I0 = S → •S, $

S → •AA, $

In changed I0 State, add all productions beginning with A since "." is followed by the non-terminal. So, it will become the I0 State

I0=  S → •S, $

S → •AA, $

A → •aA, a/b

A → •b, a/b

I1= Go to (I0, S) = closure (S → S•, $) = S → S•, $

I2= Go to (I0, A) = closure ( S → A•A, $ )

"In I2 State, add all productions beginning with A since "." is followed by the non-terminal. The I2 Condition, then, becomes

I2= S → A•A, $

A → •aA, $

A → •b, $

I3= Go to (I0, a) = Closure ( A → a•A, a/b )

In the I3 State, add all productions beginning with A since "." is followed by the non-terminal. The I3 Condition, then, becomes

I3= A → a•A, a/b

A → •aA, a/b

A → •b, a/b

Go to (I3, a) = Closure (A → a•A, a/b) = (same as I3)

Go to (I3, b) = Closure (A → b•, a/b) = (same as I4)

I4= Go to (I0, b) = closure ( A → b•, a/b) = A → b•, a/b

I5= Go to (I2, A) = Closure (S → AA•, $) =S → AA•, $

I6= Go to (I2, a) = Closure (A → a•A, $)

"In I6 State, add all productions beginning with A since "." is followed by the non-terminal. The I6 Condition, then, becomes

I6 = A → a•A, $

A → •aA, $

A → •b, $

Go to (I6, a) = Closure (A → a•A, $) = (same as I6)

Go to (I6, b) = Closure (A → b•, $) = (same as I7)

I7= Go to (I2, b) = Closure (A → b•, $) = A → b•, $

I8= Go to (I3, A) = Closure (A → aA•, a/b) = A → aA•, a/b

I9= Go to (I6, A) = Closure (A → aA•, $) = A → aA•, $

Diagram DFA:

CLR(1) Parsing Table:

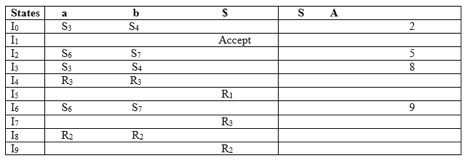
Productions are numbered according to the following:

1. S  →  AA      ... (1)                                 
2. A  → aA       ....(2)    
3. A  →  b     ... (3) 

The location of the move node in the CLR (1) parsing table is the same as the parsing table of the SLR (1).

Key takeaway:

●      To create the CLR (1) parsing table, CLR parsing utilises the canonical set of LR (1) objects.

●      As compared to the SLR (1) parsing, the CLR (1) parsing table produces a greater number of states.

LALR parser

The lookahead LR is alluded to by LALR. We use the canonical set of LR (1) objects to create the LALR (1) parsing table.

In the LALR (1) analysis, the LR (1) products that have the same outputs but look ahead differently are combined to form a single set of items

The parsing of LALR(1) is the same as the parsing of CLR(1), the only distinction in the parsing table.

LALR (1) Parsing:

LALR refers to the lookahead LR. To construct the LALR (1) parsing table, we use the canonical collection of LR (1) items.

In the LALR (1) parsing, the LR (1) items which have same productions but different look ahead are combined to form a single set of items

LALR (1) parsing is the same as the CLR (1) parsing, only difference in the parsing table.

Example

LALR ( 1 ) Grammar

1. S → AA 
2. A  → aA 
3. A → b 

Add Augment Production, insert the '•' symbol for each production in G at the first place and add the look ahead as well.

S → •S, $ 

S → •AA, $ 

A → •aA, a/b  

A → •b, a/b 

I0 State:

Add the output of Augment to the I0 State and measure Closure L

I0 = Closure (S → •S)

Add all productions beginning with S to I0 State, since the non-terminal is followed by '•'. The I0 Condition, then, becomes

I0 = S → •S, $

S → •AA, $

In changed I0 State, add all productions beginning with A since "•" is followed by the non-terminal. So, it will become the I0 State.

I0= S → •S, $

S → •AA, $

A → •aA, a/b

A → •b, a/b

I1= Go to (I0, S) = closure (S → S•, $) = S → S•, $

I2= Go to (I0, A) = closure ( S → A•A, $ )

In the I2 State, add all productions beginning with A since "•" is followed by the non-terminal.

Key takeaway:

1. The current symbol in the input string is moved into the stack for the shift operation.
2. The shifted symbol will be viewed as a single parse tree node.
3. LR(1) parser Verify the grammar's uncertainty.
4. The lookahead LR is alluded to by LALR. We use the canonical set of LR (1) objects to create the LALR (1) parsing table.

3.3 Polishing expressions Operator precedence grammar

Operator precedence parsing

The grammar of operator precedence is a kind of shift reduction system of parsing. It is applied to a small grammar class of operators.

A grammar, if it has two properties, is said to be operator precedence grammar:

●      There's no R.H.S. Of any production.

●      There are no two adjoining non-terminals.

Operator precedence can only be defined between the terminals of the grammar. A non-terminal is overlooked.

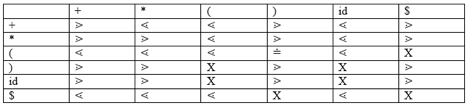
The three operator precedence relations exist:

●      a ⋗ b suggests that the precedence of terminal "a" is greater than terminal "b"

●      a ⋖b means the lower precedence of terminal "a" than terminal "b"

●      a ≐ b indicates that all terminals "a" and "b" have the same precedence.

Precedence table:

3.4 LR grammars

The LR parser is a bottom-up, non-recursive shift-reduce parser. It employs a broad range of context-free grammars, making it the most efficient syntax analysis method. LR parsers are also known as LR(k) parsers, with L denoting left-to-right scanning of the input stream, R denoting right-most derivation construction in reverse, and k denoting the number of lookahead symbols to make decisions.

Reasons for attractiveness of LR parser

●      LR parsers are capable of handling a wide range of context-free grammars.

●      The LR parsing method is a non-back tracking shift-reduce parsing method with a wide range of applications.

●      Syntax errors can be detected by an LR parser as soon as they occur.

●      LR grammars are able to describe a greater number of languages than LL grammars.

Drawbacks

●      Building an LR parser by hand is too time consuming. It necessitates the use of an automated parser generator.

●      If the grammar contains ambiguities or other constructs, a left-to-right scan of the input is difficult to parse.

3.5 Comparison of parsing methods

The following are some of the key distinctions between Top Down and Bottom Up Parsing.

3.6 Error handling

The Error Handling process' tasks are to detect each error, communicate it to the user, and then devise and apply a recovery strategy to handle the error. The program's processing time should not be slow during this entire operation. The blank entries in the symbol table are Errors.

Types or Sources of Error –

Run-time and compile-time errors are the two sorts of errors:

1. A run-time error is an error that occurs during the execution of a program and is typically caused by incorrect system parameters or improper input data. This can include a lack of memory to run an application, a memory conflict with another software, or a logical error. Logic mistakes arise when code is performed but does not generate the desired outcome. Deliberate software debugging is the best way to deal with logic flaws.
2. Before the program is executed, the number of compile-time mistakes increases. This can be a syntax error or a missing file reference that stops the application from building properly.

Classification of Compile-time error –

●      Lexical - Misspellings of identifiers, keywords, and operators fall into this category.

●      Syntactical - A semicolon is missing, or the parenthesis are imbalanced.

●      Semantical - Operator and operand type mismatches or incompatible value assignment

●      Logical - Infinite loop due to unreachable code.

Finding error or reporting an error -

A parser's viable-prefix attribute enables for early detection of syntax mistakes.

●      Goal - detection of an error as quickly as possible without wasting further input.

●      How - When the prefix of the input does not match the prefix of any string in the language, an error is detected.

●      Example - If you use for(;), you'll get an error because there are two semicolons inside the brackets.

Error recovery

1. Panic Mode Recovery

●      In this method, successive characters from input are removed one at a time until a designated set of synchronizing tokens is found. Synchronizing tokens are deli-meters such as ; or }

●      Advantage is that it's easy to implement and guarantees not to go to infinite loop.

●      Disadvantage is that a considerable amount of input is skipped without checking it for additional errors.

2.     Phase level recovery

To fix the problem, apply local correction to the input. However, under this method, error rectification is tough.

3.     Error productions

The compiler designers are aware of several frequent faults that may occur in the code. When these faults are encountered, augmented grammars can be employed as productions that yield erroneous constructs. For instance, instead of 5*x, write 5x.

4.     Global correction

Its goal is to convert an invalid input string to a legitimate string with as little changes as feasible. The implementation of this method is costly.

References:

1. Thomas W. Parsons, Introduction to Compiler Construction. Computer Science Press,1992.
2. Compiler design in C, A.C. Holub, PHI.
3. Compiler construction (Theory and Practice), A.Barret William and R.M. Bates, Galgotia Publication.
4. Https://tutorialspoint.dev/computer-science/compiler-design/error-handling-compiler-design