Unit - 6

Code optimization and code generation

6.1 Basic blocks and flow graphs

Basic blocks

The Basic Block includes a declaration sequence. The control flow enters at the beginning of the sentence and leaves without any halt at the end (except may be the last instruction of the block).

A fundamental block is generated by the following sequence of three address statements:

1. t1:= x * x 
2. t2:= x * y 
3. t3:= 2 * t2 
4. t4:= t1 + t3 
5. t5:= y * y 
6. t6:= t4 + t5

Basic block construction:

Algorithm: Partition into basic blocks

Input: It comprises the series of three sentences of address

Output: It comprises a list of basic blocks in exactly one block with three address statements each.

Method: Identify the leader in the code first. The guidelines are as follows for finding leaders:

●      The first statement is a leader.

●      Statement L is a leader if the goto statement is conditional or unconditional, such as: if....goto L or goto L

●      Instruction L is a leader if a goto or conditional goto sentence like: if goto B or goto B is followed immediately.

The basic block for each leader consists of the leader and all statements up to that. The next leader and the end of the curriculum are not included.

For the dot product of two vectors a and b of length 10, consider the following source code:

Begin  

Prod :=0;  

i:=1;  

Do begin  

Prod :=prod+ a[i] * b[i];  

i :=i+1;  

End  

While i <= 10  

End 

The three address codes for the source programme above are given below:

B1

1. (1) prod := 0  
2. (2) i := 1 

B2

1. (3) t1 := 4* i  
2. (4) t2 := a[t1]  
3. (5) t3 := 4* i  
4. (6) t4 := b[t3]  
5. (7) t5 := t2*t4  
6. (8) t6 := prod+t5  
7. (9) prod := t6  
8. (10)    t7 := i+1  
9. (11)    i := t7  
10. (12)    if i<=10 goto (3)     

The basic block B1 contains the declaration (1) to (2)

The basic block B2 contains a declaration (3) to (12)

Flow graph

A directional graph is a flow graph. It contains the control information stream for the basic block collection.

A control flow graph is used to show how the control of the programme between the blocks is parsed. It is helpful in the optimization of the loop.

The vector dot product's flow graph is given as follows:

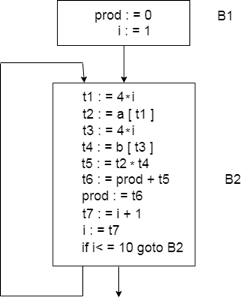
Fig 1: Flow graph

●      The initial node is block B1. Block B2 follows B1 immediately, so an edge occurs from B2 to B1.

●      The jump goal from the last statement of B1 is the first statement of B2, so there is an edge from B1 to B2.

●      B2 is a successor to B1 and the precursor to B2 is B1.

Key takeaway:

●      The Basic Block includes a declaration sequence.

●      A directional graph is a flow graph.

●      It contains the control information stream for the basic block collection.

6.2 Optimization of basic blocks

The process of optimization can be extended to a simple block. We don't need to adjust the set of expressions computed by the block during optimization.

There are two forms of simple optimization for blocks. That are like the following:

1. Structure-Preserving Transformations

The main Structure-Preserving Basic Block Transformation is as follows:

1. Common subexpression elimination

You do not need to be computed again and again in the common sub-expression. Instead, you can compute it once and store it from where it is referenced when it is again encountered.

a : = b + c 

b : = a - d  

c : = b + c                         

d : = a - d

In the expression above, the same expression was computed in the second and fourth expressions. So it is possible to transform the block as follows:

a : = b + c  

b : = a - d                                                        

c : = b + c 

d : = b

B.     Dead code elimination

●      A programme can contain a large amount of code that is dead.

●      This can be caused when once declared and defined once and forget to remove them in this case they serve no purpose.

●      Suppose the statement x:= y + z appears in a block and x is a dead symbol that means it will never subsequently be used. Then without changing the value of the basic block you can safely remove this statement.

A statement t:= b + c can be changed to u:= b + c where t is a temporary variable and u is a new temporary variable.Without modifying the basic block value, the entire instance of t can be replaced with the u.

Suppose the following two adjacent statements are given to a block:

t1 : = b + c  

t2 : = x + y 

If the value of t1 does not affect the value of t2, these two statements can be interchanged without affecting the value of the block.

2. Algebraic Transformations

●      In an algebraic transformation, the expression set can be changed into an algebraically equivalent set. The expression x:= x + 0 or x:= x *1 can thus be omitted from the basic block without altering the expression package.

●      A type of similar optimization is constant folding. We test constant expressions here at the time of compilation and substitute their values for the constant expression. Thus, 13.5 will replace the expression 5*2.7.

●      Often, relational operators such as <=, >=, <, >, +, = etc. produce an unexpected common sub-expression.

●      Associative expression is often used to reveal a common sub-expression without altering the value of the basic block. If there are assignments in the source code,

a:= b + c 

e:= c +d +b 

They will generate the following intermediate code:

a:= b + c 

t:= c +d 

e:= t + b

Key takeaway:

●      you can compute it once and store it from where it is referenced when it is again encountered.

●      The process of optimization can be extended to a simple block.

●      We don't need to adjust the set of expressions computed by the block during optimization.

6.3 Code optimization techniques

The following are some of the most important code optimization techniques:

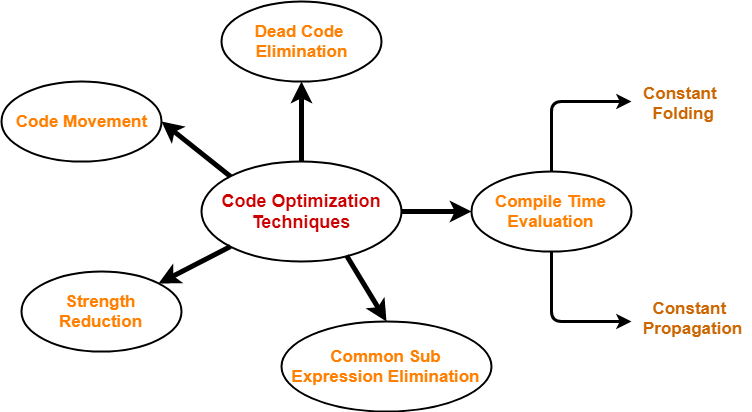
Fig 2: Code optimization technique

●      Compile Time Evaluation

●      Common subexpression elimination

●      Dead Code Elimination

●      Code Movement

●      Strength Reduction

Compile time evaluation

The following are two methodologies that fall within the category of compile time evaluation:

A) Constant Folding-

This process involves

●      It entails folding the constants, as the name implies.

●      At compile time, expressions containing operands with constant values are evaluated.

●      The results of those expressions are then substituted for them.

Example-

Circumference of Circle = (22/7) x Diameter

Here,

At build time, this approach analyzes the expression 22/7.

The result 3.14 is then substituted for the expression.

This reduces the amount of time spent on the job.

B) Constant Propagation-

This method entails

●      If a constant value has been assigned to a variable, it is replaced with that constant value in subsequent programs during compilation.

●      The requirement is that the variable's value must not change in the middle.

Example-

Pi = 3.14

Radius = 10

Area of circle = pi x radius x radius

Here,

●      At compile time, this approach replaces the values of variables 'pi' and 'radius.'

●      The expression 3.14 x 10 x 10 is then evaluated.

●      The result 314 is then substituted for the expression.

●      This reduces the amount of time spent on the job.

Common Subexpression Elimination-

Common Sub-Expression refers to an expression that has previously been computed and exists in the code for computation.

This method entails

●      It entails removing the common sub phrases, as the name implies.

●      To avoid re-computation, the redundant expressions are removed.

●      When necessary, the previously computed result is used in the subsequent program.

Example-

Code Movement-

This method entails

●      It involves the movement of the code, as the name implies.

●      If it doesn't matter whether the code is present inside or outside the loop, it is moved out.

●      With each iteration of the loop, this code is executed unnecessarily again.

●      This wastes time during the execution phase.

Example-

Dead Code Elimination-

This method entails

●      It entails removing the dead code, as the name implies.

●      The code statements that are never executed, are unreachable, or whose output is never used are removed.

Example-

Strength Reduction-

This method entails

●      It entails lowering the intensity of expressions, as the name implies.

●      This method substitutes simple and less expensive operators for the more expensive and time-consuming ones.

Example

Here,

The term "A x 2" has been substituted with "A + A."

This is due to the fact that the multiplication operator is more expensive than the addition operator.

6.4 Issues in design of code generator

Various problems may occur in the code generation phase:

1. Input to the code generator

●      The code generator input contains the intermediate representation of the source programme and the symbol table information. The front end creates the source programme.

●      The multiple choices have intermediate representation:

1. Postfix notation
2. Syntax tree
3. Three address code

●      We assume that the front end generates a low-level intermediate representation, i.e. the system instructions may directly control the values of names in it.

●      The code generation stage requires maximum intermediate code that is error-free as required by an input.

2.  Target program

The output of the code generator is the target programme. The performance could be:

1. Assembly language: It enables the compilation of subroutines separately.
2. Relocatable machine language: It makes the code generation process simpler.
3. Absolute machine language: It can be stored in memory at a fixed location and can be executed right away.

3. Memory management

●      The symbol table entries have to be mapped to individual p addresses during the code generation process and levels have to be mapped to the instruction address.

●      The front end and code generator agree with the mapping name in the source programme to address data.

●      In the activation record, local variables are stack allocation, while global variables are in the static field

4. Instruction selection

●      The design of the target machine's instruction set should be complete and consistent.

●      If the performance of the target machine is considered, then the speed of instruction and machine idioms are important considerations.

●      Its speed and size will decide the quality of the produced code.

Example:

The Three address code is:

t:= w + x

y:= t + z

Inefficient assembly code is:

MOV w, R0              R0→w                             

ADD x, R0   R0        x+ R0 

MOV R0, t               t  →   R0 

MOV t, R0             R0→  t

ADD z, R0                R0  →       z + R0 

MOV R0, y               y    →  R0 

5. Register allocation

The register can be reached more easily than the memory. The instructions for registry operations are shorter and faster than those for memory operations.

When we use registers, the following sub-issues emerge:

1. Register allocation: We pick the set of variables in the registry allocation that will reside in the register.
2. Register assignment: We choose the register containing a variable in the register assignment

For certain operands and outcomes, certain devices need even-odd pairs of registers.

Example

Consider the form's following division instruction:

D a,b

Where,

a -  dividend even register in even/odd register pair

b - divisor

Even register is used to hold the reminder.

Old register is used to hold the quotient.

6. Evaluation order

The effectiveness of the goal code can be influenced by the order in which the calculations are conducted. Some calculation orders require fewer registers than others to carry intermediate data.

Key takeaway:

●      The code generator input contains the intermediate representation of the source programme and the symbol table information.

●      The code generation stage requires maximum intermediate code that is error-free as required by an input.

●      The register can be reached more easily than the memory.

6.5 Target machine code and simple code generator

●      For designing a good code generator, familiarity with the target machine and its instruction set is a prerequisite.

●      A byte-addressable machine with 4 bytes per word is the target computer.

●      It contains n registers for general purposes, R0, R1, . , the Rn-1.

●      The form has two address instructions:

Op source, destination

Where, op is used as an op-code and the data field is used as source and destination.

●      It has the op-codes below

SUB (subtract source from destination)

MOV (move source to destination)

ADD (add source to destination)

●      A combination of registers and memory location with address modes can specify the source and destination of an instruction.

Example: MOV R0, M, for example, stores Register R0 contents in memory location M.

Instruction costs:

●      Instruction cost = 1+ cost for the address modes of source and destination. The duration of the instruction corresponds to this expense.

●      The cost of address modes involving registers is zero.

●      Address modes that include position or literal memory cost one.

●      If space is important, instruction length should be reduced. Doing so often minimises the time taken to fetch the instruction and execute it.

Example: MOV R0, R1, for example, copies the contents of the R0 register to R1. It cost one, because it only occupies one word of memory.

●      Via several different instruction sequences, the three-address statement a:= b+c can be implemented:

1. MOV b, R0

ADD c, R0 cost = 6 MOV R0, a

1. MOV b, a

ADD c, a cost = 6

1. Assuming that R0, R1 and R2 contain a, b, and c, addresses:

MOV *R1, *R0

ADD *R2, *R0 cost = 2

●      We have to use its addressing capabilities effectively to produce good code for the target computer.

Simple Code generator

A code generator generates target code for a series of three-address statements and stores the operands of the statements in registers.

Take, for example, the three-address formula a:= b+c. It could have the following code sequence:

ADD Rj, Ri Cost = 1

(or)

ADD c, Ri Cost = 2

(or)

MOV c, Rj Cost = 3

ADD Rj, Ri

Register and Address Descriptors:

A register descriptor keeps track of what's in each register at any given time. According to the register descriptors, all of the registers are initially empty.

The location where the current value of the name can be found at run time is stored in an address descriptor.

Key takeaway

●      For designing a good code generator, familiarity with the target machine and its instruction set is a prerequisite.

●      A byte-addressable machine with 4 bytes per word is the target computer.

References:

1. Alfred V. Aho, Ravi Sethi, Jeffrey D. Ullman, Monica S. Lam, Compilers: Principles, Techniques, and Tools. Addison‐Wesley, 2006 (optional).
2. Compiler design in C, A.C. Holub, PHI.
3. Compiler construction (Theory and Practice), A.Barret William and R.M. Bates, Galgotia Publication.
4. Https://www.gatevidyalay.com/code-optimization-techniques/